Горюнов В.П. (ред.) Формирование профессиональной культуры специалистов 21 века в техническом университете. Сборник научных трудов
Подождите немного. Документ загружается.

111
нутой кривой, называемой предельным циклом. Таким образом, в системе
устанавливается автоколебательный процесс.
При
c
BB <
положение равновесия устойчиво, и система ведёт себя со-
вершенно иначе. Концентрации X и Y совершают затухающие колебания,
приближаясь к своим равновесным значениям: при
∞
→
t
AX
→
,
ABY /
→
. Изображающая точка на фазовой плоскости в этом случае асим-
птотически стремится к положению равновесия, т.е. к точке с координа-
тами (A;B/A). При этом возможны два случая. Если
1
1
2
22
+
<
<
+
−
A
B
A
A
,
точка равновесия (A;B/A) является устойчивым фокусом, а концентрации
X и Y совершают затухающие колебания около своих равновесных значе-
ний. Если же
1
2
2
+
−
<
A
A
B
, то точка равновесия является устойчивым уз-
лом, и затухающие колебания концентраций X и Y носят апериодический
характер. Сравним теперь результаты решения системы (1) при различных
значениях B, полагая
2
=
A
. В этом случае
5
=
c
B
. Решение проводилось с
помощью пакета Mathcad методом Рунге – Кутта четвёртого порядка.
На рис. 1 представлен результат решения системы (1) при
2
=
A
;
6
=
B
с начальными условиями
8,1)0(
=
X
;
3,3)0(
=
Y
. Поскольку в данном случае
c
BB >
, то, как следует из вышесказанного, образуется предельный цикл.
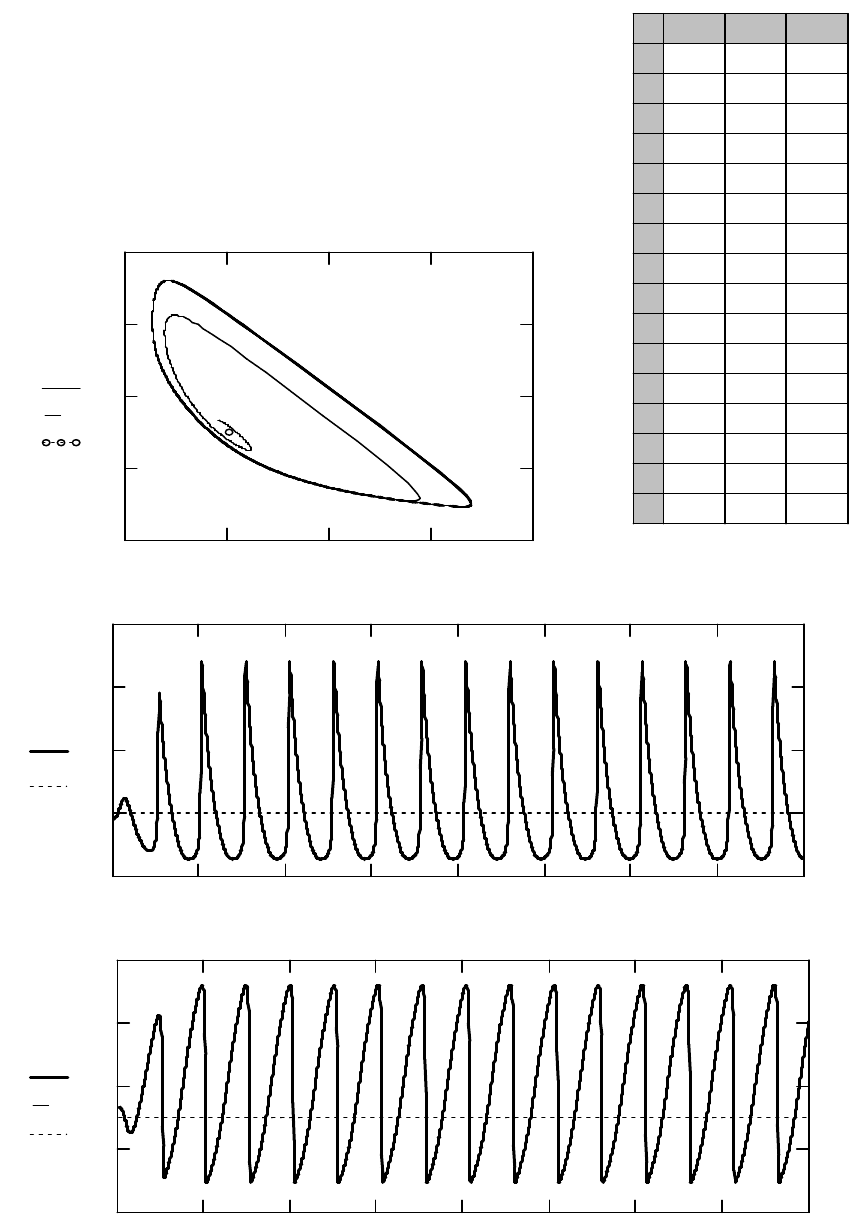
Это видно из верхнего графика рис. 1. Этот график представляет собой
фазовую траекторию. Светлой точкой на фазовой плоскости изображено
положение равновесия, т.е. точка с координатами (2; 3). Кроме того, по-
скольку выполнено условие
1
2
2
+
+
<
A
A
B
, точка равновесия (2; 3) пред-
ставляет собой неустойчивый фокус. Действительно, на фазовой траекто-
рии видна раскручивающаяся спираль. На втором и третьем графиках рис.
1 представлены соответственно зависимости концентраций X и Y от вре-
мени. Видно, что амплитуды колебаний этих концентраций возрастают,
приближаясь к своим предельным значениям. На рис. 2 представлен ре-
зультат решения системы (1) при тех же значениях A и B, что и на рис. 1
(
2
=
A
;
6
=
B
), но с новыми начальными условиями:
3,1)0(
=
X
;
9,1)0(
=
Y
.
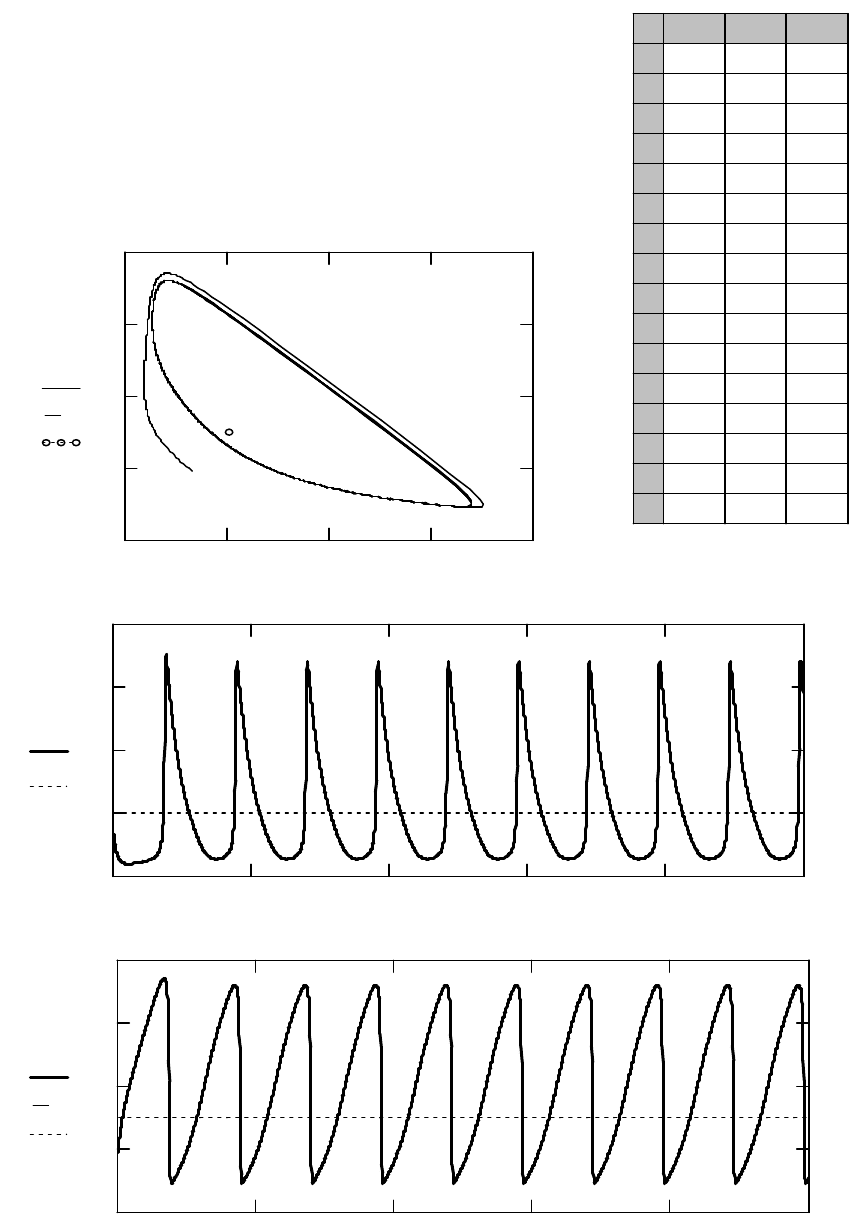
Параметры A и B в данном случае имеют такие же значения, что и на рис.
1, поэтому образуется такой же предельный цикл. Это иллюстрирует тот
факт, что образующийся предельный цикл не зависит от начальных усло-
вий, а определяется лишь параметрами системы. Анализ двух последую-
щих графиков рис. 1 и 2 показывает, что и периоды установившихся ко-
лебаний концентраций X и Y на обоих графиках также одинаковы. На рис.
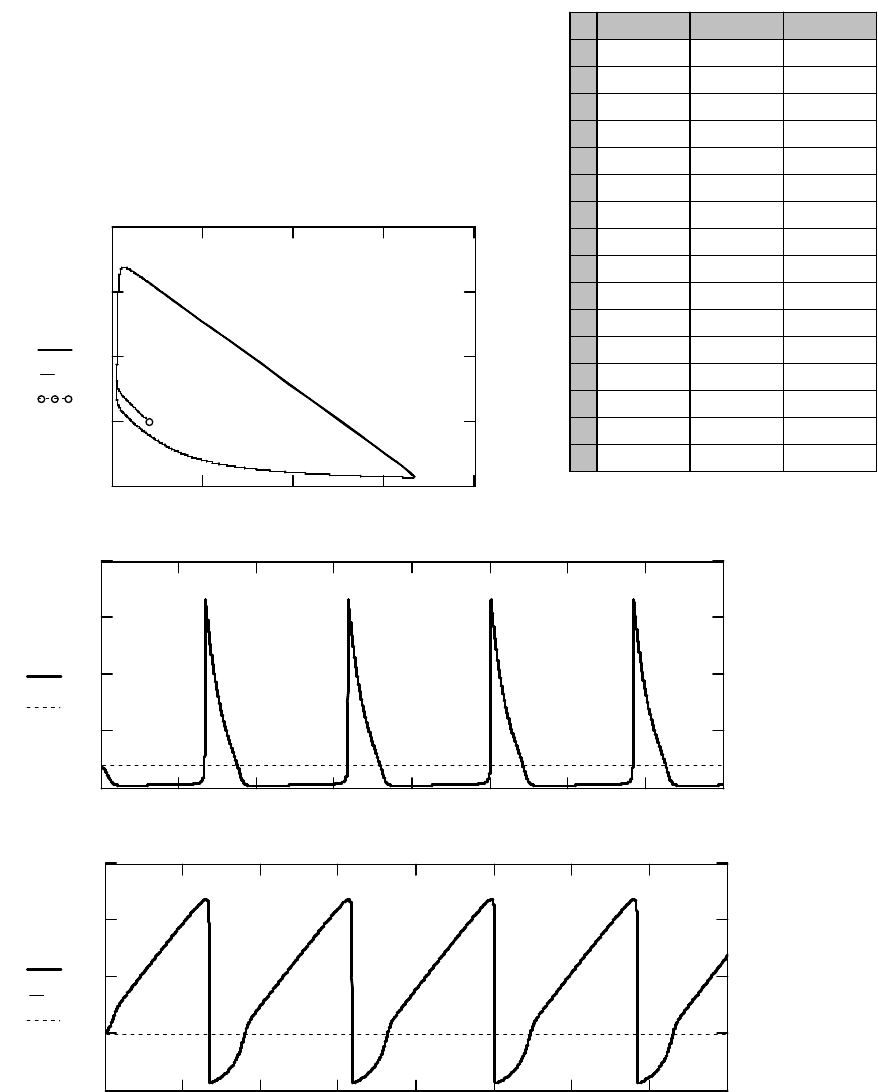
3 представлен результат решения системы (1) при
2
=
A
;
10
=
B
с началь-
ными условиями
8,1)0(
=
X
;
2,5)0(
=
Y
. Поскольку в данном случае
c
BB >
и
1
2
2
+
+
>
A
A
B
, то образуется предельный цикл, и точка равновесия (2; 5)
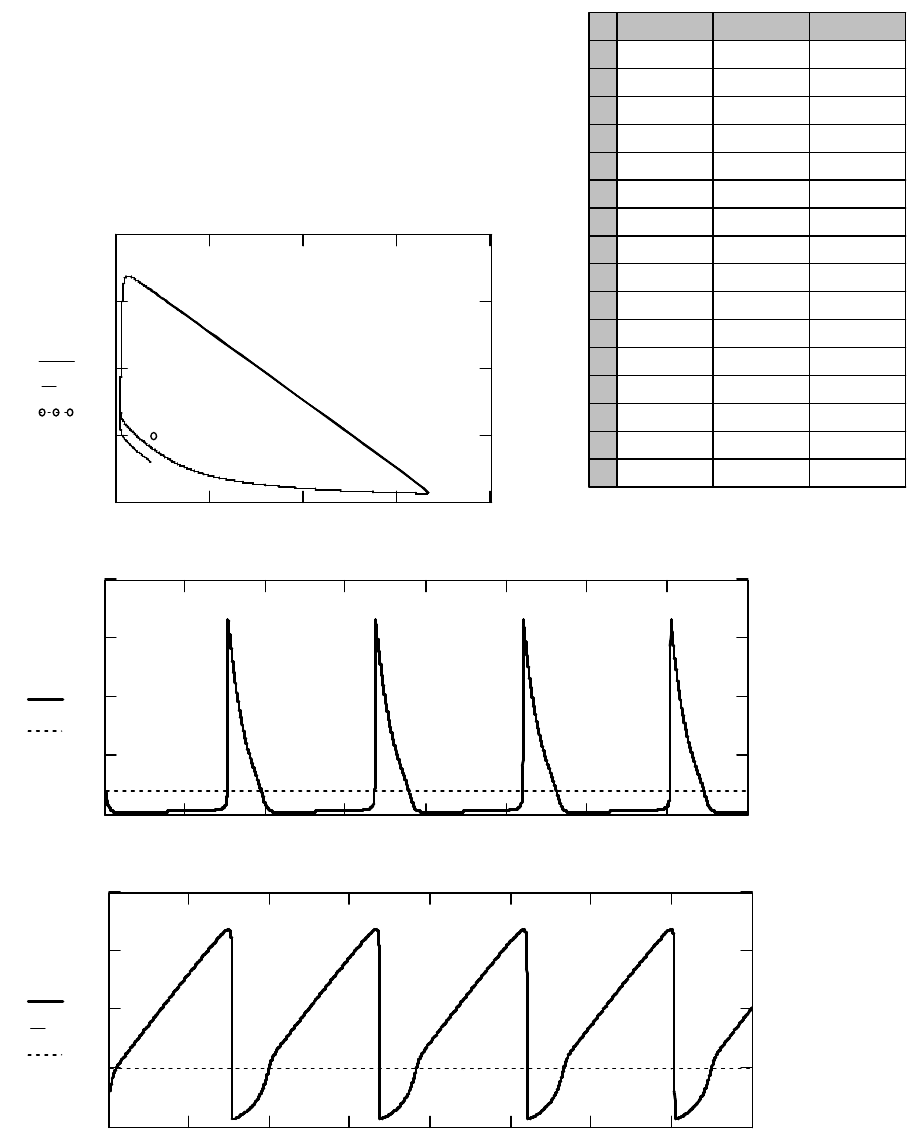
является уже неустойчивым узлом. На рис. 4 представлен результат ре-
шения системы (1) при тех же значениях A и B, что и на рис. 3 (
2
=
A
;
10
=
B
), но с новыми начальными условиями:
8,1)0(
=
X
;
3)0(
=
Y
. Посколь-
ку в этом случае параметры A и B имеют такие же значения, что и на рис.
3, то образуется такой же предельный цикл.
112
A 2:= B 6:=
x
1.8
3.3
:=
D t x,( )
A B 1+( ) x
0
⋅− x
0
( )
2
x
1
⋅+
B x
0
⋅ x
0
( )
2
x
1
⋅−
:=
Z rkfixed x 0, 80, 3200, D,( ):=
0 2 4 6 8
0
2
4
6
8
Z
2
〈 〉
B
A
Z
1
〈 〉
A,
Z
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 1.8 3.3
0.025 1.803 3.302
0.05 1.806 3.304
0.075 1.809 3.305
0.1 1.813 3.306
0.125 1.818 3.306
0.15 1.823 3.305
0.175 1.829 3.303
0.2 1.836 3.301
0.225 1.843 3.298
0.25 1.851 3.294
0.275 1.86 3.289
0.3 1.869 3.283
0.325 1.879 3.276
0.35 1.889 3.268
0.375 1.901 3.26
=
t1 0 80..:=
0 10 20 30 40 50 60 70 80
0
2
4
6
8
Z
1
〈 〉
A 0 t1⋅+
Z
0
〈 〉
t1,
0 10 20 30 40 50 60 70 80
0
2
4
6
8
Z
2
〈 〉
B
A
0 t1⋅+
Z
0
〈 〉
t1,
Рис. 1. Результат решения системы дифференциальных уравнений (1)
при
2
=
A
;
6
=
B
с начальными условиями:
8,1)0(
=
X
;
3,3)0(
=
Y
113
A 2:= B 6:=
x
1.3
1.9
:=
D t x,( )
A B 1+( ) x
0
⋅− x
0
( )
2
x
1
⋅+
B x
0
⋅ x
0
( )
2
x
1
⋅−
:=
Z rkfixed x 0, 50, 3200, D,( ):=
0 2 4 6 8
0
2
4
6
8
Z
2
〈 〉
B
A
Z
1
〈 〉
A,
Z
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 1.3 1.9
0.016 1.241 1.97
0.031 1.186 2.038
0.047 1.134 2.103
0.063 1.085 2.166
0.078 1.038 2.227
0.094 0.995 2.286
0.109 0.954 2.343
0.125 0.915 2.398
0.141 0.879 2.452
0.156 0.845 2.504
0.172 0.813 2.554
0.188 0.782 2.603
0.203 0.754 2.651
0.219 0.727 2.698
0.234 0.702 2.743
=
t1 0 50..:=
0 10 20 30 40 50
0
2
4
6
8
Z
1
〈 〉
A 0 t1⋅+
Z
0
〈 〉
t1,
0 10 20 30 40 50
0
2
4
6
8
Z
2
〈 〉
B
A
0 t1⋅+
Z
0
〈 〉
t1,
Рис. 2. Результат решения системы дифференциальных уравнений (1) при
2
=
A
;
6
=
B
с начальными условиями:
3,1)0(
=
X
;
9,1)0(
=
Y
114
A 2:= B 10:=
x
1.8
5.2
:=
D t x,( )
A B 1+( ) x
0
⋅− x
0
( )
2
x
1
⋅+
B x
0
⋅ x
0
( )
2
x
1
⋅−
:=
Z rkfixed x 0, 40, 18500, D,( ):=
0 5 10 15 20
0
5
10
15
20
Z
2
〈 〉
B
A
Z
1
〈 〉
A,
Z
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 1.8 5.2
2.162·10
-3
1.798 5.203
4.324·10
-3
1.796 5.205
6.486·10
-3
1.794 5.208
8.649·10
-3
1.792 5.21
0.011 1.789 5.213
0.013 1.787 5.215
0.015 1.785 5.218
0.017 1.783 5.221
0.019 1.781 5.223
0.022 1.779 5.226
0.024 1.776 5.229
0.026 1.774 5.231
0.028 1.772 5.234
0.03 1.769 5.237
0.032 1.767 5.24
=
t1 0 40..:=
0 5 10 15 20 25 30 35 40
0
5
10
15
20
Z
1
〈 〉
A 0 t1⋅+
Z
0
〈 〉
t1,
0 5 10 15 20 25 30 35 40
0
5
10
15
20
Z
2
〈 〉
B
A
0 t1⋅+
Z
0
〈 〉
t1,
Рис. 3. Результат решения системы дифференциальных уравнений (1)
при
2
=
A
;
10
=
B
с начальными условиями:
8,1)0(
=
X
;
2,5)0(
=
Y
115
A 2:= B 10:=
x
1.8
3
:=
D t x,( )
A B 1+( ) x
0
⋅− x
0
( )
2
x
1
⋅+
B x
0
⋅ x
0
( )
2
x
1
⋅−
:=
Z rkfixed x 0, 40, 18500, D,( ):=
0 5 10 15 20
0
5
10
15
20
Z
2
〈 〉
B
A
Z
1
〈 〉
A,
Z
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 1.8 3
2.162·10
-3
1.783 3.018
4.324·10
-3
1.765 3.036
6.486·10
-3
1.748 3.053
8.649·10
-3
1.731 3.071
0.011 1.714 3.088
0.013 1.698 3.106
0.015 1.681 3.123
0.017 1.664 3.14
0.019 1.648 3.157
0.022 1.632 3.174
0.024 1.616 3.191
0.026 1.6 3.208
0.028 1.584 3.225
0.03 1.568 3.242
0.032 1.552 3.258
=
t1 0 40..:=
0 5 10 15 20 25 30 35 40
0
5
10
15
20
Z
1
〈 〉
A 0 t1⋅+
Z
0
〈 〉
t1,
0 5 10 15 20 25 30 35 40
0
5
10
15
20
Z
2
〈 〉
B
A
0 t1⋅+
Z
0
〈 〉
t1,
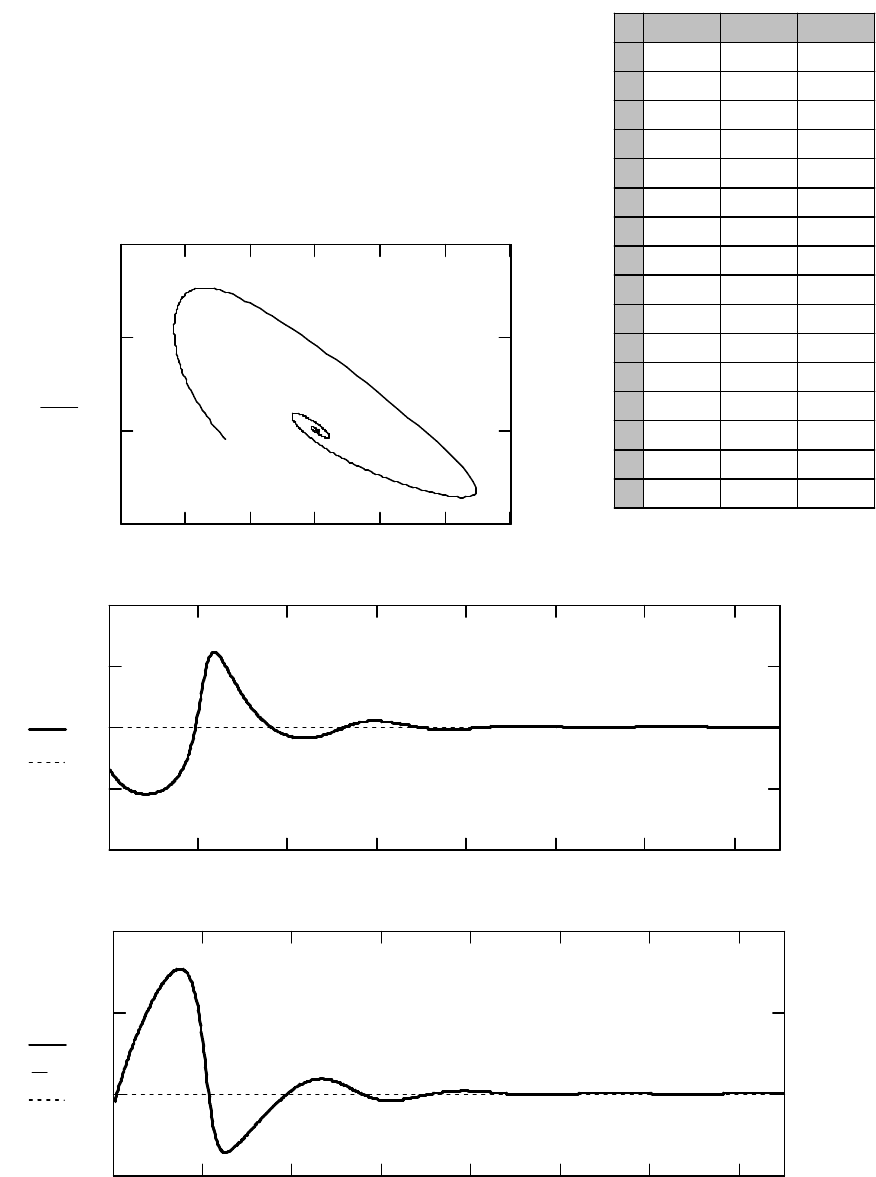
Рис. 4. Результат решения системы дифференциальных уравнений (1)
при
2
=
A
;
10
=
B
с начальными условиями:
8,1)0(
=
X
;
3)0(
=
Y
116
A 2:= B 4:=
x
1.3
1.9
:=
D t x,( )
A B 1+( ) x
0
⋅− x
0
( )
2
x
1
⋅+
B x
0
⋅ x
0
( )
2
x
1
⋅−
:=
Z rkfixed x 0, 15, 800, D,( ):=
0.5 1 1.5 2 2.5 3 3.5
1
2
3
4
Z
2
〈 〉
Z
1
〈 〉
Z
0 1 2
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
14.719 1.999 2.001
14.738 1.999 2.001
14.756 1.999 2.001
14.775 2 2.001
14.794 2 2.001
14.813 2 2.001
14.831 2 2.001
14.85 2 2.001
14.869 2 2.001
14.888 2 2.001
14.906 2 2.001
14.925 2 2.001
14.944 2 2.001
14.963 2 2.001
14.981 2 2.001
15 2 2
=
t1 0 15..:=
0 2 4 6 8 10 12 14
0
1
2
3
4
Z
1
〈 〉
A 0 t1⋅+
Z
0
〈 〉
t1,
0 2 4 6 8 10 12 14
1
2
3
4
Z
2
〈 〉
B
A
0 t1⋅+
Z
0
〈 〉
t1,
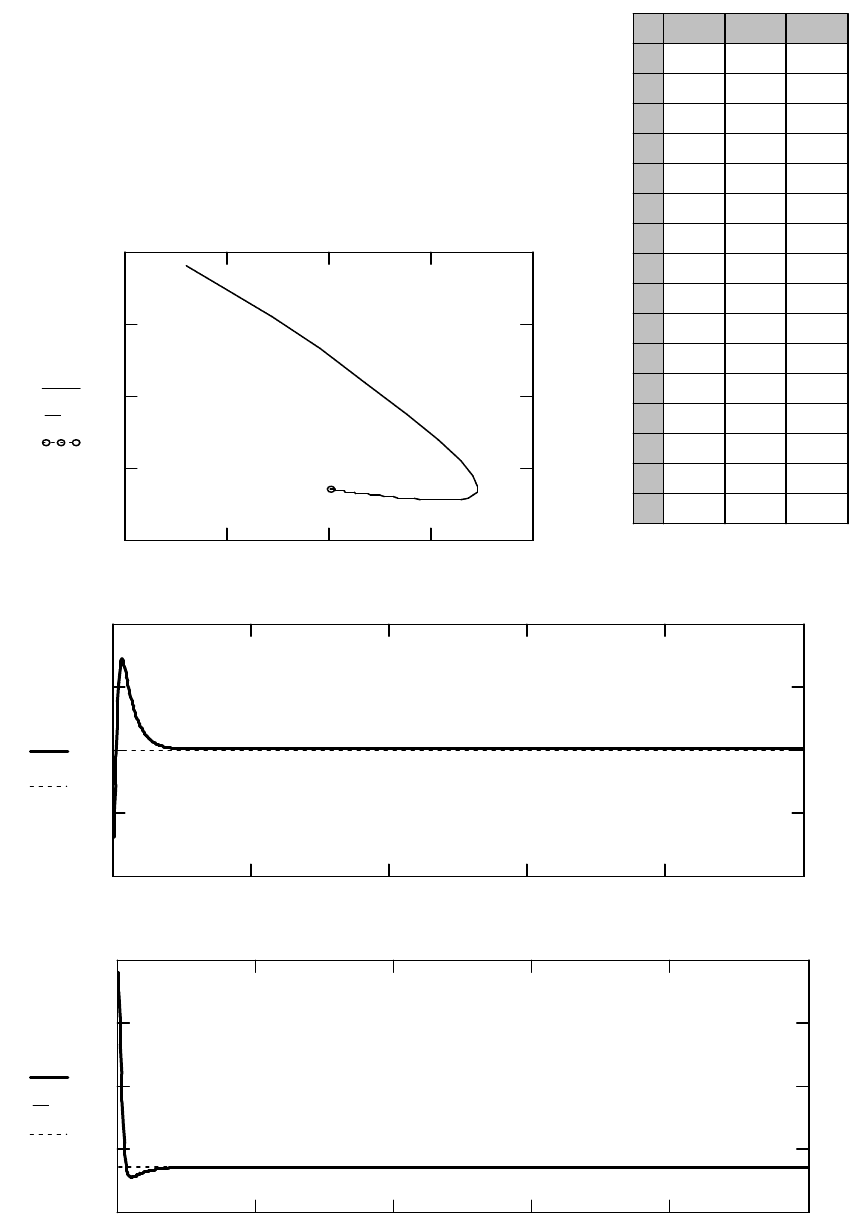
Рис. 5. Результат решения системы дифференциальных уравнений (1)
при
2
=
A
;
4
=
B
с начальными условиями:
3,1)0(
=
X
;
9,1)0(
=
Y
117
A 2:= B 0.7:=
x
1.3
1.9
:=
D t x,( )
A B 1+( ) x
0
⋅− x
0
( )
2
x
1
⋅+
B x
0
⋅ x
0
( )
2
x
1
⋅−
:=
Z rkfixed x 0, 50, 800, D,( ):=
1 1.5 2 2.5 3
0
0.5
1
1.5
2
Z
2
〈 〉
B
A
Z
1
〈 〉
A,
Z
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 1.3 1.9
0.063 1.499 1.739
0.125 1.718 1.544
0.188 1.949 1.323
0.25 2.176 1.093
0.313 2.377 0.875
0.375 2.534 0.689
0.438 2.64 0.545
0.5 2.7 0.443
0.563 2.724 0.375
0.625 2.723 0.331
0.688 2.705 0.304
0.75 2.677 0.288
0.813 2.645 0.279
0.875 2.61 0.275
0.938 2.575 0.273
=
t1 0 50..:=
0 10 20 30 40 50
1
1.5
2
2.5
3
Z
1
〈 〉
A 0 t1⋅+
Z
0
〈 〉
t1,
0 10 20 30 40 50
0
0.5
1
1.5
2
Z
2
〈 〉
B
A
0 t1⋅+
Z
0
〈 〉
t1,
Рис. 6. Результат решения системы дифференциальных уравнений (1)
при
2
=
A
;
7,0
=
B
с начальными условиями:
3,1)0(
=
X
;
9,1)0(
=
Y
118
На рис. 5 представлен результат решения системы (1) при
2
=
A
;
4
=
B
с начальными условиями
3,1)0(
=
X
;
9,1)0(
=
Y
. В данном случае
1
1
2
22
+
<
<
+
−
A
B
A
A
, так что точка равновесия (2; 2) является устойчивым
фокусом. Действительно, фазовая траектория представляет собой скручи-
вающуюся спираль (см. верхний график рис. 5). Концентрации X и Y в
этом случае совершают затухающие колебания около своих равновесных
значений (см. второй и третий графики рис. 5).
На рис. 6 представлен результат решения системы (1) при
2
=
A
;
7,0
=
B
с начальными условиями:
3,1)0(
=
X
;
9,1)0(
=
Y
. Поскольку в данном
случае
1
2
2
+
−
<
A
A
B
, точка равновесия (2; 0,35) является устойчивым уз-
лом. Это видно и из верхнего графика, который представляет собой фазо-
вую траекторию. В этом случае концентрации X и Y совершают апериоди-
ческие затухающие движения, асимптотически приближаясь к своим рав-
новесным значениям (см. второй и третий графики рис. 6).
Таким образом, в данном докладе представлены результаты подробно-
го исследования брюсселятора на устойчивость и описаны все возможные
типы точки равновесия. Результаты компьютерного решения могут быть
использованы в качестве компьютерной лекционной демонстрации по те-
ме «Самоорганизация» при преподавании дисциплины «Концепции со-
временного естествознания» [1].
Библиография
1. Примерная программа дисциплины «Концепции современного естествознания».
Министерство образования Российской Федерации. ГНИИ ИТТ «Информатика» (Ин-
тернет-публикация). – М.: 2000.
2. Романов В.П. Концепции современного естествознания. – М.: Вузовский учеб-
ник, 2008. – 282 с.
3. Томпсон Дж. М. Т. Неустойчивости и катастрофы в науке и технике. – М.: Мир,
1985. – С. 125-130.
4. Пригожин И., Николис Ж. Биологический порядок, структура и неустойчивости
// Успехи физических наук, 1973, т. 109, вып. 3, С. 517-544.
5. Пригожин И. Время, структура и флуктуации // Успехи физических наук, 1980,
т. 131, вып. 2, С. 185-207.
6. Малинецкий Г.Г. Математические основы синергетики: Хаос, структуры, вы-
числительный эксперимент. – М.: ЛКИ, 2007. – С. 216-218.
7. Пригожин И. От существующего к возникающему: Время и сложность в физи-
ческих науках. – М.: Наука, 1985. – С. 112-113.

119
Н.Н. Серостанова
ДИДАКТИЧЕСКИЕ ФУНКЦИИ ТЕЛЕКОММУНИКАЦИОННЫХ
ПРОЕКТОВ В ПРОЦЕССЕ ФОРМИРОВАНИЯ
ЛИЧНОСТНО-ПРОФЕССИОНАЛЬНОЙ КОМПЕТЕНЦИИ
БУДУЩИХ СПЕЦИАЛИСТОВ
Воронеж,
Воронежский государственный технический университет
Модернизация теории и практики российского образования, связанная
с изменениями социально-экономической реальности, требует подготовки
высококвалифицированных специалистов, владеющих высоким уровнем
личностно-профессиональной компетенции.
Личностно-профессиональную компетенцию (ЛПК) следует рассмат-
ривать как комплекс личностных свойств будущего специалиста, способ-
ствующих повышению продуктивности его профессиональной деятельно-
сти, становлению личности и индивидуальности профессионала (В. И.
Байденко, В.Е. Буденкова, Е.Н.Савельева, Е. М. Ядченко, и др.)
Одним из наиболее эффективных направлений, способствующих фор-
мированию ЛПК студентов является участие в телекоммуникационных
проектах, которые открывают новые возможности в организации процес-
са профессионального овладения иностранным языком, позволяет инди-
видуализировать обучение, активизировать учебно-познавательную дея-
тельность обучающихся, приблизить ее к профессиональной.
Телекоммуникационный проект (ТП) представляет собой совместную
учебно-познавательную, исследовательскую, творческую или игровую
деятельность обучающихся, организованную на основе компьютерной те-
лекоммуникации, имеющую общую проблему, цель, согласованные мето-
ды и способы решения проблемы, направленные на достижение совмест-
ного результата (Е.С.Полат, 2002).
Для определения специфики ТП в процессе формирования ЛПК спе-
циалистов, необходимо остановиться на их дидактических функциях. Под
дидактическими свойствами того или иного средства обучения понима-
ются основные характеристики, признаки этого средства, отличающие их
от других, их назначение, роль в учебно-воспитательном процессе для
достижения определенных дидактических целей… (Е.С.Полат, 1998).
В данном исследовании под дидактическими функциями ТП следует
понимать внешнее проявление сущностных свойств, возможностей, при-
знаков и характеристик ТП, используемых в процессе подготовки специа-
листов в ВУЗе с целью формирования ЛПК.
Анализ литературы по рассматриваемой проблеме (Полат Е.С., Бухар-
кина М.Ю., Моисеева М.В., Дмитриева Е.И., Пахмутова Е.Д. и др.) позво-
120
ляет выделить основные дидактические функции ТП в процессе формиро-
вания ЛПК будущих специалистов:
• организационная, состоящая в организации различного рода совме-
стных исследовательских работ студентов и преподавателей из различных
вузов разных регионов или стран. ТП дает возможность организовать при
этом исследовательскую, творческую либо самостоятельную деятельность
партнеров с использованием многообразия методов и форм самостоятель-
ной познавательной и практической творческой деятельности.;
• информационная, включающая оперативный поиск и обмен инфор-
мацией, идеями, планами по интересующим участников вопросам, темам
совместных профессионально-направленных проектов, расширяя таким
образом свой кругозор, повышая свой уровень профессионализма;
• интерактивная, направленная на интерактивное взаимодействие
преподавателя и студентов, проявляющееся в создании атмосферы доб-
рожелательности и взаимной поддержки, которые приводят к взаимопо-
ниманию, совместному решению общих, но значимых для каждого участ-
ника задач ТП;
• мотивационная, заключающаяся в создание возможности для от-
дельных обучающихся раскрыть свои способности, познать и проявить
свою индивидуальность, повысить интерес и мотивацию к овладению
иностранным языком специальности при подготовке, оформлении и пре-
зентации профессионально-значимого конечного продукта деятельности;
• интегративная, реализация которой заключается в формировании
целостной системы лингво-профессиональных знаний студентов и инди-
видуальных качеств в их единстве в ходе осуществления проекта.
Выявленные дидактические функции профессионально-направленных
ТП доказывают, что ТП являются весьма перспективным направлением
лингво-профессиональной подготовки специалистов в условиях инфор-
мационного общества, имеющего гуманитарно-личностную направлен-
ность, которые позволяют обеспечить возможность формировать ЛПК
будущих специалистов.
