Горлач В.В. и др. Лабораторный практикум по колебательным и волновым процессам
Подождите немного. Документ загружается.

Геометрическое место частиц среды, колеблющихся в одина-
ковой фазе, образует волновую поверхность. В зависимости от её
формы различают плоские, сферические и цилиндрические волны. В
данной работе исследуются плоские волны, волновые поверхности
которых представляют собой множество параллельных друг другу
плоскостей.
Пусть источник плоской волны находится в начале координат и
возбуждает колебания частиц упругой среды по закону ξ = Acosωt.
Частица среды, которая находится в состоянии равновесия на
расстоянии x от источника, придёт в движение по гармоническому
закону через промежуток времени
x
, где υ – скорость распростра-
нения волны. Уравнение колебания этой частицы
= A cos t−
x
, (24.1)
где ξ – смещение частиц среды с координатой х в момент времени t ;
A – амплитуда колебаний; ω = 2πν = 2π/T – угловая частота;
ν – частота; Т – период колебаний.
Уравнение плоской гармонической волны (24.1) позволяет в
любой момент времени t и в любом месте с координатой x определить
смещение ξ(х, t) любой точки, участвующей в волновом процессе.
Если в формуле (24.1) зафиксируем величину t, сделав как бы
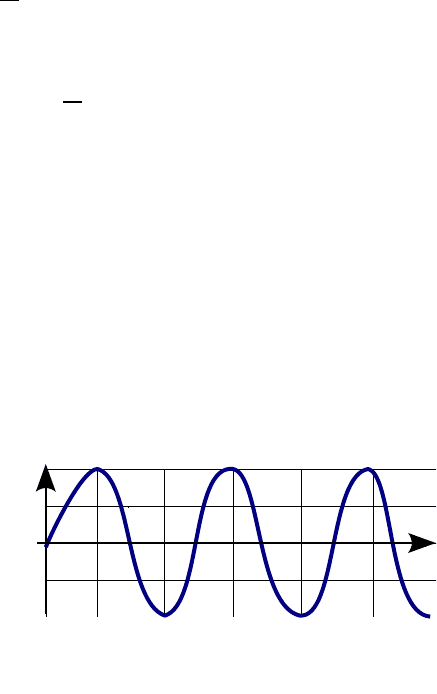
моментальный снимок волны, то получим синусоиду (рис. 24.1).
Точки среды А и B колеблются
синфазно, точнее – с разностью фаз
δ = 2π, поскольку периодичность
функции cosφ составляет 2π рад. То
же относится к точкам C и D.
Периодичность колебательного про-
цесса в пространстве характери-
зуется длиной волны λ.
Длина волны – это расстояние между ближайшими точками
среды, колеблющимися с разностью фаз 2π рад.
Легко видеть, что длина волны равна расстоянию, на которое
перемещается волновая поверхность со скоростью υ за время, равное
периоду T колебаний частиц среды: λ = υ∙Т, или
λ = υ/ν . (24.2)
51
|
Рис. 24.1. Гармоническая волна
х
ξ
|← λ →|
← λ →|
С
•
D
•
B
•
A
•
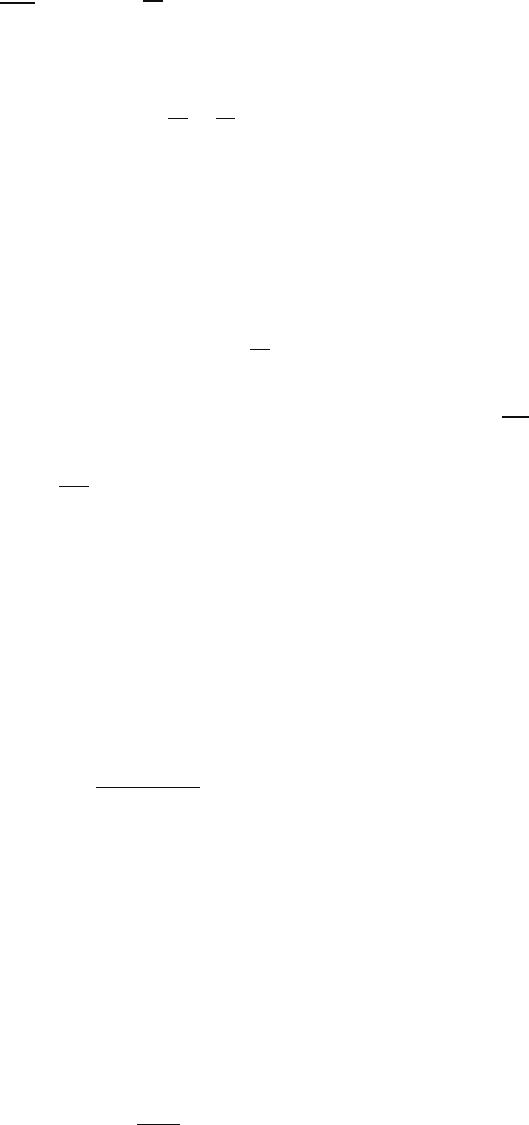
Учитывая, что
2
T
π
ω
=
и
T
λ
υ
=
, запишем уравнение плоской
волны (24.1) в другом виде:
cos2 ( )
t x
A
T
ξ π
λ
= −
, (24.3)
из которого следует, что состояние колебания (фаза) в бегущей волне
повторяется и во времени (через промежуток t = n∙T), и в
пространстве (через интервал координат Δx = n∙λ ), где n = 1, 2, 3, ... .
Определим скорость, с которой перемещается волновая поверх-
ность, имеющая заданную фазу
φ = t−
x
= C
= const. Положе-
ние этой поверхности определяется координатой
x = t−
C
.
Скорость её перемещения
dx
dt
υ
=
. Таким образом, величина υ в
уравнении (24.1) оказывается равной скорости распространения
волновой поверхности с заданной фазой и потому называется
фазовой скоростью.
Скорость распространения упругих волн зависит от температуры,
от вида деформации, от плотности и упругих свойств среды. Скорость
звуковых волн в газах, приближенных к идеальному, вычисляется по
формуле
=
γ RT / M
, (24.4)
где M – молярная масса; T – температура газа; R – молярная газовая
постоянная; γ – коэффициент Пуассона (для воздуха γ = 1, 40).
Измерив температуру воздуха, можно рассчитать теоретическое
значение скорости звука в воздухе, зная характеристики газа γ и M.
Формулу для вычисления длины волны по результатам измерений
в данной работе получим из уравнения (24.3). Легко видеть, что две
точки с координатами x
1
и x
2
колеблются со сдвигом фаз
φ
1
−φ
2
=
2 π
λ
x
2
−x
1
. (24.5)
Если разность фаз равна π, то расстояние между точками
составляет (по определению длины волны)
x
2
– x
1
=
λ /2
. (24.6)
Отсюда следует формула для вычисления длины волны
52
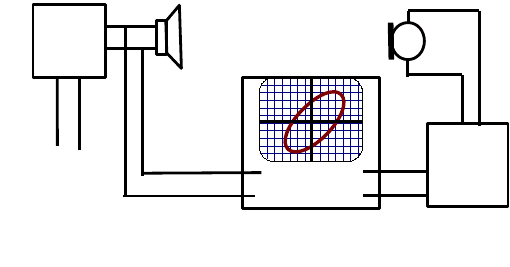
2 1
2( )x x
λ
= −
, или λ = 2s, (24.7)
где s = (x
2
– x
1
) – расстояние между точками среды, колеблющимися с
разностью фаз π рад.
Скорость звука можно вычислить на основании (24.2) и (24.7):
= 2 s⋅
. (24.8)
Таким образом, измерив две соседние координаты (x
1
и x
2
) точек
бегущей волны, для которых разность фаз φ
1
– φ
2
= π, можно
определить длину волны, а затем и скорость звука, зная частоту.
Разность фаз определяется в данной работе с помощью осциллографа.
Цель работы: ознакомиться с методом измерения длины звуковой
волны; определить длину волны и скорость звука в воздухе на разных
частотах; выяснить характер зависимостей: а) длины волны от
частоты; б) скорости звука от частоты; в) длины волны от расстояния
между источником и приемником звуковых волн.
Приборы: динамик и микрофон, установленные на скамье с
линейной шкалой; звуковой генератор; усилитель; осциллограф.
Описание установки
От звукового генератора 3Г (рис. 24.2) на динамик Д и
одновременно на вход X осциллографа О подаётся напряжение,
изменяющееся по гармоническому закону. Микрофон М улавливает
звуковые волны, излучаемые динамиком Д. Механические колебания
мембраны микрофона преобразуются в электрические колебания и
подаются на вход усилителя низкой частоты УНЧ. Усиленный сигнал
поступает на вход Y осциллографа.
На пути от динамика к
микрофону звуковые колеба-
ния приобретают некоторую
разность фаз (24.5) δ = φ
1
– φ
2
,
зависящую от координаты ми-
крофона относительно дина-
мика. Электронный луч осцил-
лографа принимает участие в
двух взаимно-перпендикуляр-
ных колебаниях одинаковой
частоты, но отличающихся по фазе. В результате сложения этих
колебаний луч на экране описывает замкнутую кривую линию, в
53
~220 В
Рис. 24.2. Блок-схема установки
ЗГ
УНЧ
○
○
Д
М
О
○
○
X Y
○ ○
0 5 10 15 20 25
| | | | | | | | | | | | | | | | | | | | | | | | | | | |
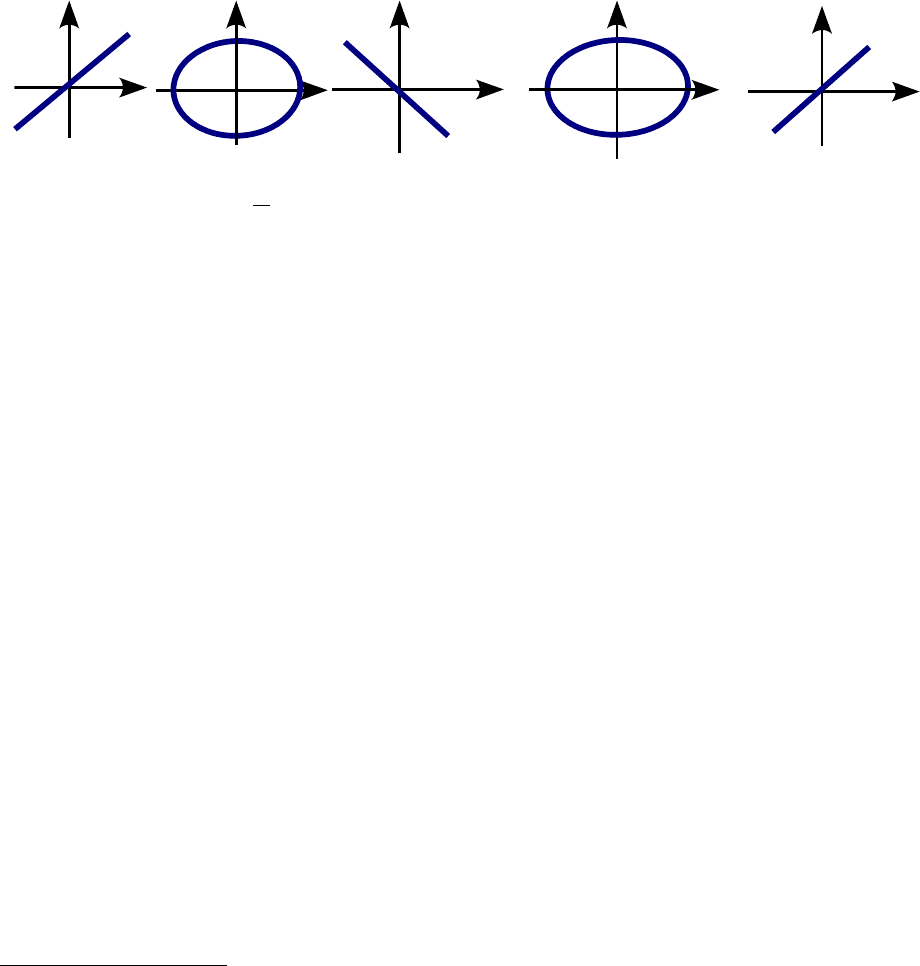
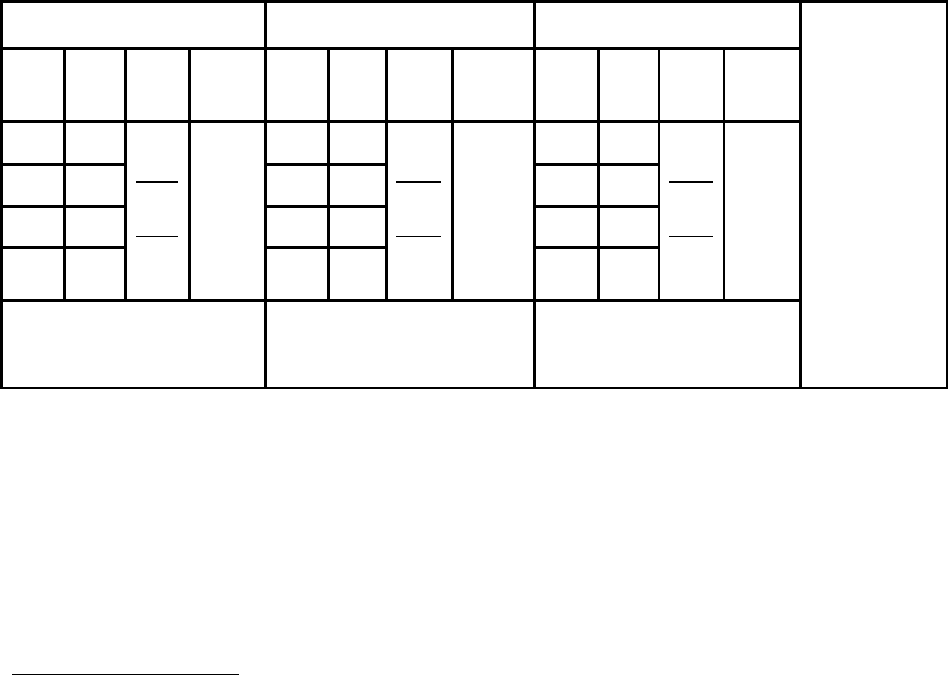
общем случае – эллипс, форма и ориентация которого зависит от
разности фаз δ. Из теории колебаний известно
32
, что при δ = 0
траектория луча – это прямая линия, проходящая в первом и третьем
квадрантах через начало декартовой системы координат (рис. 24.3, а).
Если δ = π осциллограмма вновь приобретает вид прямой линии, но
расположенной по-другому: она проходит из второго квадранта через
начало координат в четвертый квадрант (рис. 24.3, в). Когда δ = 2π –
это вновь прямая линия, проходящая через первый и третий
квадранты (рис. 24.3, д), т. е. траектория электронного луча
приобретает свою первоначальную форму, как и при разности фаз
δ = 0.
Таким образом, если наблюдается полное повторение вида
осциллограммы в результате смещения микрофона по направлению
распространения звуковой волны, то это означает, что фаза колебаний
мембраны микрофона изменилась на 2π, т. е. состояние колебаний в
звуковой волне, дошедшей до микрофона, то же, что и в его
начальном положении. Следовательно (по определению длины
волны), микрофон сместился на одну длину волны.
В данной работе фиксируются изменения вида осциллограммы от
а к в или от в к д (см. рис. 24.3) при смещении микрофона вдоль
распространения звука. При этом изменение фазы колебаний равно π
рад, а отсчитываемая при этом разность координат микрофона (24.6)
принимается равной половине длины звуковой волны.
Выполнение работы
1. Собрать цепь по схеме (рис. 24.1); включить звуковой
генератор, осциллограф, усилитель.
32 См. теорию к лабораторной работе 17.
54
y y y y y
x x x x x
а) δ = 0 б) δ =
π
2
в) δ = π г) δ = ³/
2
π д) δ = 2π
Рис. 24.3. Результаты сложения взаимно‑перпендикулярных
колебаний одинаковой частоты при различной разности фаз
2. Ознакомиться с ручками управления, находящимися на
передней панели осциллографа (см. работу 17, рис. 17.4). Установить
частоту генератора около 3 кГц и амплитуду его выходного сигнала,
достаточную для получения эллипса оптимального размера в
пределах экрана осциллографа (см. рис. 24.1). С помощью
соответствующих ручек управления электронным лучом добиться
чёткого изображения.
3. Перемещая микрофон вблизи динамика, получить на экране
осциллографа изображение прямой линии (рис. 24.3, а или 24.3, в);
записать в табл. 24.2 координату микрофона x
1
по шкале линейки.
4. Медленно удалять микрофон от динамика, пока луч на экране
не станет снова вычерчивать прямую линию, но лежащую в другой
паре квадрантов. Записать в таблицу координату x
2
.
Таблица 24.1
Результаты измерения длины волны и скорости звука
ν
1
= ... кГц ν
2
= ... кГц ν
3
= ... кГц
<υ>
эксп
=
… м/c;
υ
теор
=
… м/с;
υ
табл
=
… м/с
x↑,
см
x↓,
см
s,
см
<s
1
>,
см
x↑,
см
x↓,
см
s,
см
<s
2
>,
см
x↑,
см
x↓,
см
s,
см
<s
3
>,
см
λ
1
= … ± ...
υ
1
= … ± …
λ
2
= … ± …
υ
2
= … ± …
λ
3
= … ± …
υ
3
= … ± …
5. Продолжая удалять микрофон, найти новые координаты
x
3
и x
4
,
где на экране получается прямая линия
33
. Координаты x
1
, x
2
, x
3
, x
4
записывать в первый столбец (х↑, см. табл. 24.1).
6. Приближая микрофон к источнику звука, повторить измерения
координат x
4
, x
3
, x
2
, x
1
. Результаты записать во второй столбец (х↓).
33 Для уменьшения случайной погрешности величины s = (x
2
– х
1
) следует зафиксировать не
менее четырёх осциллограмм, когда приёмник звука последовательно занимает положения с
координатами x
1
, ... x
4
, где эллипс превращается в прямую вида а или в (рис. 24.3). Эти
данные также помогут ответить на вопрос, зависит или не зависит длина звуковой волны от
от координаты приёмника звука относительно источника звука.
55
7. Вычислить расстояния s = x
n+1
– x
n
между найденными сосед-
ними положениями микрофона, где x
n+1
и x
n
– средние значения
координаты микрофона по двум столбцам (х↑ и х↓); n – номера
измерений (n = 1, 2, 3 ). Найти среднее <s>, если значения s, получен-
ные при различном удалении микрофона от динамика, совпадают с
учётом погрешностей измерений.
8. Вычислить длину волны (24.7) и скорость звука (24.8).
9. Выполнить действия, указанные в пп. 3 – 8, на других частотах
генератора ν
2
и ν
3
(ν
2
> ν
1
;
ν
3
> ν
1
).
10. Вычислить относительную погрешность
λ
=
λ
λ
измерения
длины звуковой волны на одной из частот ν
1
, ν
2
, ν
3
(по указанию
преподавателя). Вычислить абсолютные погрешности: Δλ
1
= δ
λ
∙λ
1
;
Δλ
2
= δ
λ
∙λ
2
; Δυ
3
= δ
λ
∙λ
3
. Записать результаты λ
1
, λ
2
и λ
3
в виде:
λ = <λ> ± Δλ. Анализируя полученные данные, сделать вывод о
зависимости (или независимости) длины звуковой волны от частоты
и от координаты относительно источника звука.
11. Вычислить относительную погрешность
=
скорости
звука для одной из частот ν
1
, ν
2
, ν
3
(по указанию преподавателя).
Вычислить абсолютные погрешности: Δυ
1
= δ
υ
∙υ
1
; Δυ
2
= δ
υ
∙υ
2
;
Δυ
3
= δ
υ
∙υ
3
. Записать результаты υ
1
, υ
2
и υ
3
в виде: υ
= <υ> ± Δυ. Сделать
вывод о наличии (или об отсутствии) дисперсии звука в воздухе
34
.
12. По трём значениям скорости звука, измеренной при разных
частотах, найти (если доверительные интервалы скоростей пере-
секаются) среднее <υ> и сравнить его с теоретическим значением,
рассчитанным по формуле (24.4) и с табличным (табл. 24.2)
35
.
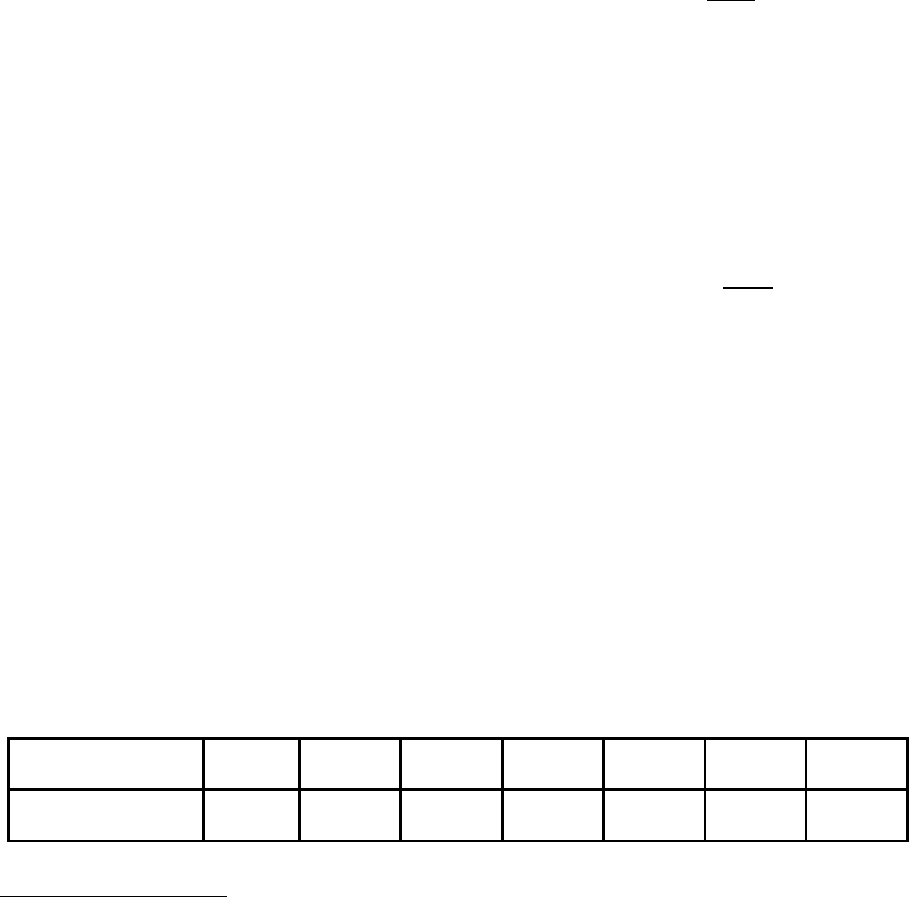
Таблица 24.2
Скорость звука в воздухе при различных температурах
t,
о
С – 150 – 50 0 10 20 30 100
υ, м/с 216,7 299,3 331,5 337,3 343,1 348,9 387,1
34 Дисперсией волн [от лат. dispersio – рассеяние] называют зависимость фазовой скорости от
частоты.
35 Когда температура опыта не совпадает ни с одним значением, представленным в таблице,
тогда искомое табличное значение скорости находится методом линейной интерполяции [4].
56
13. Сформулировать и записать общие выводы по работе.
Совпадение всех трёх значений: экспериментального, расчётного и
табличного – можно считать подтверждением справедливости
теоретических положений, заложенных в основу метода измерений:
теории сложения взаимно-перпендикулярных колебаний, формулы
(24.4) и уравнения бегущей волны (24.1).
Контрольные вопросы
Допуск
1. Объяснить смысл понятий: а) звуковая волна; б) фаза волны.
2. Дать определение длины волны.
3. Зависимость длины волны от фазовой скорости (формула-закон).
4. Какие непосредственные измерения нужно выполнить, чтобы экспе-
риментально определить длину звуковой волны в данной работе?
5. Каково расстояние между двумя ближайшими точками волны в направ-
лении её распространения, если они колеблются: а) с разностью фаз π
(в противофазе); б) с разностью фаз 2π (синфазно)?
6. При какой разности фаз и каком соотношении амплитуд двух вза-
имно-перпендикулярных колебаний одной частоты осциллограмма резуль-
тирующего колебания имеет вид: а) окружности; б) прямой линии?
Защита
7. В чем сходство и различие понятий «волновая поверхность» и «фронт
волны»?
8. Вывести уравнение плоской волны, взяв за основу уравнение гармони-
ческих колебаний с начальной фазой, равной нулю.
9. Изобразить графически: а) мгновенное распределение смещения частиц,
участвующих в волновом движении; б) зависимость смещения одной из
частиц от времени.
10. Звук частотой 1 кГц имеет в воздухе длину волны 380 мм. Какой станет
станет длина волны на частоте 2 кГц при той же температуре воздуха?
11. *Длина волны в воздухе, измеренная на частоте 1 кГц, оказалась равной
35 см. При какой температуре проводились измерения?
12. Записать формулу, из которой следует, что волна представляет собой
периодический процесс и во времени, и в пространстве?
13. *Показать, что фазовая скорость – это скорость распространения
волновой поверхности с заданной фазой колебаний.
57
14. Как зависит (уменьшается, увеличивается, линейно, нелинейно)
скорость звука в газах: а) от температуры; б) от молярной массы?
15. Объяснить, почему амплитуда колебаний для всех точек плоской волны
не меняется при удалении от источника, а амплитуда сферических волн
уменьшается. (Рассеянием энергии пренебречь.)
16. Вывеcти формулу для расчёта скорости звука по результатам измерений
в данной работе.
17. Измерение какой величины вносит наибольшую погрешность при
определении скорости звука на данной установке?
18. *Что такое волновой вектор? Для чего вводится величина
k = 2π/λ? Записать уравнение плоской бегущей волны с использованием
волнового числа.
19. *Что называется волновым уравнением? Какая связь существует между
волновым уравнением и уравнением плоской бегущей волны?
20. *Материальная точка участвует в двух взаимно-перпендикулярных
колебаниях с одинаковыми частотами. Разность фаз Δφ = π/2 рад. Получить
уравнение траектории у(х) и указать на рисунке направление скорости
движения.
21. Уравнение волны имеет вид
3
0,1sin(10 4 )t x
ξ
= −
, где ξ – смещение
частиц, м; х – координата частицы, м; t – время, с. Определить период
колебаний частиц и фазовую скорость волны.
22. *При известной длине звуковой волны данный метод можно исполь-
зовать для измерений перемещения микрофона относительно источника
звука. Как зависит точность измерений от частоты?
23. *Объяснить зависимость скорости звука в воздухе от высоты над
поверхностью Земли.
58

Лабораторная работа 25
СТОЯЧИЕ ЗВУКОВЫЕ ВОЛНЫ В ТРУБЕ
Рекомендуемая литература
[14]. § 99. С. 289. Стоячие волны.
[15]. §157. С. 287. Стоячие волны.
Основы теории
36
Рассмотрим наложение двух встречных плоских волн
37
с одина-
ковой частотой ω и амплитудой А. Уравнения этих волн задаются
выражениями:
для прямой волны
1
= A cost −
x
= Acos 2π
t
T
−
x
λ
,
для встречной волны, идущей в обратную сторону,
2
= Acost
x
= A cos2π
t
T
x
λ
.
Результирующее смещение
=
1
2
.
Используя теорему о сложении косинусов, получим уравнение
стоячей волны.
= 2 Acos
2 π
λ
x⋅cos t
. (25.1)
На практике стоячие волны возникают при отражении бегущих
волн от преград. Падающая и отражённая волны, налагаясь друг на
друга, при определенных условиях образуют стоячую волну.
Соотношение (25.1) показывает, что в стоячей волне все точки
упругой среды колеблются по гармоническому закону с той же
угловой частотой ω, что и в падающей бегущей волне. Амплитуда
стоячей волны А
ст
является гармонической функцией координаты x:
A
ст
= 2 Acos
2π
λ
x
. (25.2)
Зависимости смещения частиц ξ от координаты x для моментов
времени t = 0 и t = ½T показаны на рис. 25.1. Все точки среды, в
которой установилась стоячая волна, в моменты времени t = ¼ Т и
36 См. также теорию к работе 24.
37 Наложение волн, согласованных по частоте и по фазе, сопровождаемое устойчивым во
времени перераспределением энергии волнового движения в пространстве, называется
интерференцией.
59
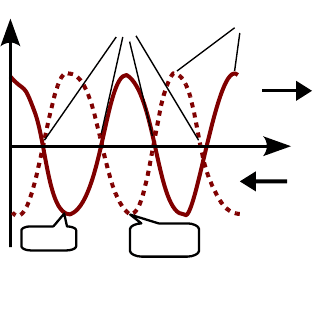
t = ¾T находятся в положении равновесия (ξ = 0). Точки среды, в
которых амплитуда колебаний максимальна и равна 2A, называются
пучностями стоячей волны, а точки, в которых амплитуда равна нулю,
– узлами (точки А, B, C и D).
Волна называется стоячей потому, что координаты узлов и
пучностей не изменяются со временем. Из рис. 25.1 видно, что узлы и
пучности отстоят друг от друга на четверть длины волны λ/4, а
расстояние между соседними пучностями,
как и между соседними узлами, равно
половине длины бегущей волны λ/2. Все
точки между соседними узлами колеб-
лются с одинаковой фазой. Разность фаз
колебаний точек по разные стороны от
узла составляет π рад, т. е. их колебания
совершаются «в противофазе».
Рассмотренная выше теория описы-
вает стоячие волны в неограниченных или
полуограниченных упругих средах. В ограниченных средах (телах)
стоячие волны возникают только в тех случаях, когда в промежутке
между отражающими поверхностями укладывается нечётное или
чётное число четвертей длин волн (λ/4) в зависимости от граничных
условий. В частности, в ограниченных столбах газа стоячие волны
образуются, когда у открытых концов трубы находятся пучности, а у
закрытых концов – узлы.
Обоснование метода измерений
Для измерения длины звуковой волны в данной работе
используется метод стоячих волн. Упругая среда (воздух), в которой
создаются волны, находится в трубе (рис. 25.2). Один из концов трубы
закрыт подвижным поршнем П. У другого (открытого) конца
расположен источник звука – телефон Т .
Колебания частиц воздуха, возбуждаемые мембраной телефона,
распространяются вдоль трубы. Звуковая волна доходит до поршня,
отражается от него и далее распространяется навстречу падающей
волне. Происходит наложение двух встречных волн – падающей и
отражённой.
Если на длине ℓ воздушного столба укладывается нечётное число
четвертей длин волн
60
2А
λ/4 λ/2 λ/2 λ/2 λ/4
Рис.25.1. Узлы и пучности
стоячей волны
x
υ
отр
υ
пад
ξ Узлы Пучности
0
t = 0
t = T/2
A B C D
