Горлач В.В. и др. Лабораторный практикум по колебательным и волновым процессам
Подождите немного. Документ загружается.

параллельной ей прямой); K
Y
– число точек пересечения фигуры с
осью Y (или с параллельной ей прямой).
3.4. Сравнить значения ν
Y
,
полученные с помощью осциллографа
по фигурам Лиссажу, с результатами непосредственных отсчётов
частоты по шкале звукового генератора ν
Y(ЗГ)
. Сделать вывод.
Контрольные вопросы
Допуск
1. На какие пластины: горизонтально или вертикально отклоняющие,
подается:
а) исследуемое напряжение? б) напряжение развёртки?
2. Наименования основных электродов ЭЛТ; их роль в формировании
электронного луча и управления им.
3. Назначение генератора развёртки; форма вырабатываемых им-
пульсов.
4. Из осциллограмм А – D, представленных на рис. 17.7, выбрать ту,
которая реализуется в случае, когда к ЭЛТ приложено:
а) только исследуемое переменное напряжение (развёртка отключена);
б) постоянное исследуемое напряжение (развёртка отключена); в) только
развёртывающее напряжение.
5. По осциллограммам А – D (см. рис. 17.7) определить, в каких случаях
переменное напряжение приложено:
а) к пластинам Х; б) к пластинам Y; в) и к пластинам Х, и пластинам Y.
Защита
6. Описать осциллографический метод измерения амплитуды
гармонических колебаний.
7. Как определяется период исследуемых колебаний по осциллограмме,
если известен период развёртки?
21
А
В
C
Рис.17.7. Виды осциллограмм
D
8. Определить частоту исследуемого сигнала по осциллограмме С
(см. рис. 17.7), если частота развертки: а) 1 кГц; б) 2 кГц.
9. Зарисовать осциллограмму, наблюдаемую в случае, когда на вход Х и
на вход Y поданы синусоидальные напряжения одинаковой частоты и
амплитуды при разности фаз, равной: а) ½π рад; б) π рад; в) 0.
10. Как изменится вид осциллограммы периодического сигнала, если
период развёртки увеличить (уменьшить) в два раза?
11. Как изменится осциллограмма периодического сигнала, если увели-
чить (уменьшить) положительный потенциал ускоряющего анода ЭЛТ
относительно катода?
12. Описать методику определения частоты синусоидальных колебаний
по фигуре Лиссажу.
13. В чём преимущество электронного осциллографа перед другими
электроизмерительными приборами при измерениях переменного
напряжения?
14. Какое значение имеет свойство послесвечения люминесцирующего
вещества, которым покрыт экран осциллографа?
15. *Каковы приблизительно пределы измерения используемого в работе
электронного осциллографа: а) по частоте; б) по амплитуде напряжения?
16. *Доказать, что траектория электронного луча в плоскости экрана
ЭЛТ у(x) имеет вид синусоиды, если на вход Y подано синусоидальное
напряжение U
y
= U
oy
∙sinωt, а на вход Х – напряжение, прямо
пропорциональное времени, U
x
= k∙t. Известно также, что смещения луча
вдоль координатных осей пропорциональны приложенным напряжениям:
y = C
y
∙U
y
и x = C
х
∙U
х
, где C
y
и С
x
– постоянные.)
17. *Какими способами можно преобразовать механические колебания в
электрические?
22
Лабораторная работа 20
ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК СВОБОДНЫХ
КОЛЕБАНИЙ ПО ВИБРОГРАММЕ
Рекомендуемая литература
[7]. §3.1.1. С. 242. Кинематика и динамика колебательных процессов;
§3.1.3. С. 252. Затухающие колебания.
[3]. §5.9.1. С. 183. Дифференциальное уравнение затухающих колеба-
ний, его решение; §5.9.2. С. 184. Характеристики, вводимые для описания
затухающих колебаний.
Теоретическое обоснование методики измерений
Графическое изображение колебательных процессов различной
природы может быть получено на экране осциллографа, компьютера
или на бумажной ленте. Простейший виброграф
10
состоит из часового
механизма, который с постоянной скоростью протягивает бумажную
ленту. К ленте прижато перо, связанное посредством рычагов с
объектом исследования (деталью машины или элементом строитель-
ной конструкции).
После кратковременного воздействия на деталь она некоторое
время совершает свободные колебания. При этом перо прибора,
участвуя одновременно в двух взаимно-перпендикулярных движениях
относительно бумаги (прямолинейном и колебательном), выписывает
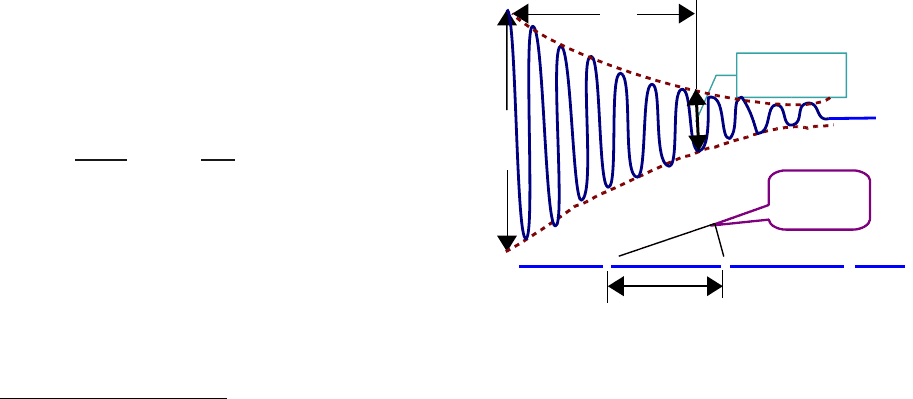
кривую, называемую виброграммой (рис. 20.1). Другое перо, связанное
с часовым механизмом, вычерчивает прямую линию с метками
времени.
Дифференциальное уравнение
свободных колебаний имеет вид
d
2
x
dt
2
2⋅
dx
dt
ω
0
2
x = 0
,
где β – коэффициент затухания;
ω
0
= 2πν
0
– собственная угловая час-
тота; ν
0
– собственная частота
(частота при отсутствии сопротив-
ления в колебательной системе).
10 Виброграф – прибор для записи колебательного движения (лат. vibrare – дрожать,
колебаться + греч. graphõ – пишу).
23
Метки
Рис. 20.1.
Виброграмма свободных колебаний
A
τ
= A
0
∙e
-βτ
l
τ
l
ms
А
0
времени

Решение этого уравнения найдено в виде функции
x = A
0
⋅e
−t
⋅cosωt φ
0
.
Амплитуда свободных колебаний из-за наличия в любой реальной
системе неупругих деформаций и сил сопротивления уменьшается по
экспоненциальному закону
A = A
0
∙e
−t
, (20.1)
где A
0
– начальная амплитуда (А = А
0
в начальный момент времени
t = 0 ); е – основание натуральных логарифмов (е = 2,718...).
Если промежуток времени, за который амплитуда убывает в е раз,
определить как время релаксации
11
τ, то из (20.1) понятен физический
смысл коэффициента затухания: коэффициент затухания – величина,
обратная времени релаксации
ф
=
1
τ
. (20.2)
Состояние свободных колебаний в точности не повторяется,
поскольку амплитуда уменьшается со временем, поэтому свободное
колебание называют условно периодическим движением. Тем не менее
колеблющаяся величина обращается в нуль, достигает максимума и
минимума через равные промежутки времени, что позволяет при
описании свободных колебаний употреблять термины: период Т
(промежуток времени, за который совершается одно колебание) и
частота ν (число колебаний за одну секунду).
Угловая частота ω свободных колебаний меньше собственной
угловой частоты ω
0
:
=
0
2
− β
2
. При уменьшении коэффициента
затухания величина ω быстро приближается к ω
0
и может быть ей
приравнена: ω ≈ ω
0
, если β → 0.
Отношение двух амплитуд, измеренных через определённый
промежуток времени t, не зависит от времени. Если t = Т, то
полученное отношение A
t
/A
t+T
называется декрементом
12
колебаний.
На практике чаще используется логарифмический декремент Λ –
величина, равная натуральному логарифму отношения амплитуд,
измеренных через период,
11 Встречаются и другие названия промежутка времени, за который амплитуда колебаний
становится меньше начальной в е раз: постоянная времени переходного процесса и также
среднее время жизни колебательного состояния.
12 Декремент (от лат. decrementum – убавление) – величина, характеризующая быстроту
затухания.
24
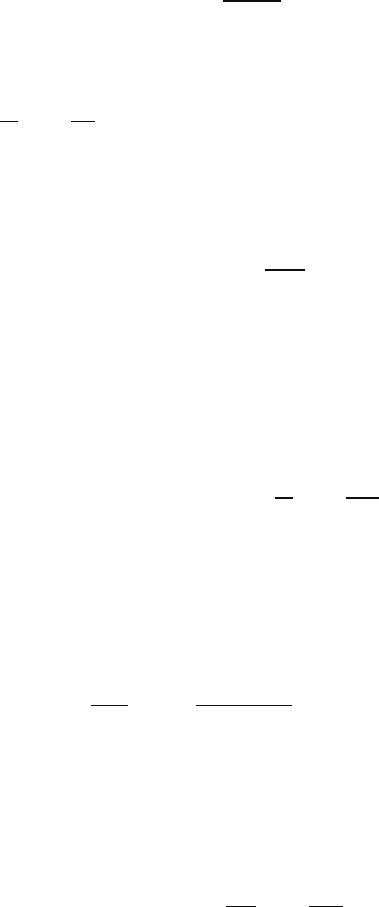
= ln
A
t
A
tT
(формула-определение). (20.3)
Если амплитуды в (20.3) заменить их выражениями (20.1) и
учесть
β
ф
=
1
τ
и
τ
T
= N
τ
,то становится ясным простой физиче-
ский смысл величины Λ: логарифмический декремент – величина,
обратная числу колебаний за время релаксации,
ф
=
1
N
. (20.4)
Для экспериментального определения коэффициента затухания
необходимо измерить амплитуды A
0
и A
t
соответственно в начале и в
конце выбранного промежутка времени t. Согласно закону (20.1)
получаем расчётную формулу
β =
1
t
⋅ln
A
0
A
t
. (20.5)
Из формулы (20.3) выводим взаимосвязь логарифмического
декремента с коэффициентом затухания, используя закон (20.1)
изменения амплитуды со временем.
= ln
A
0
A
T
= ln
A
0
A
0
⋅e
−T
= ln e
βT
=> Λ = β∙Т. (20.6)
Отсюда, учитывая (20.5), получим формулу для расчёта
логарифмического декремента по результатам непосредственных
измерений
=
1
N
⋅ln
A
0
A
t
, (20.7)
где N – число колебаний, происходящих за промежуток времени t.
Цель работы: ознакомиться с принципом работы вибрографа,
научиться определять по виброграмме характеристики свободных
колебаний: время релаксации τ; коэффициент затухания β; период
колебаний Т; логарифмический декремент Λ; убедиться, что
характеристики свободных колебаний Т, β, Λ не зависят от времени;
по результатам эксперимента проверить справедливость закона
изменения амплитуды со временем
A = A
0
∙e
−t
.
25

2. Выполнение работы
2.1. Измерение времени релаксации
1. Провести верхнюю и нижнюю огибающую амплитуд (штри-
ховые линии на рис. 20.1).
2. Измерить амплитуду А
0
у начала виброграммы, где амплитуда
13
достаточно велика.
3. Вычислить амплитуду A
τ
=
A
0
/2,718
в конце времени релак-
сации. Результаты измерений и вычислений занести в таблицу.
Результаты изучения затухающих колебаний
t
ms
= … c; ℓ
ms
= … мм; t
ms
/ℓ
ms
= … c/мм
A
0
= ...
..
мм; A
τ
=
A
0
2,718
= ... мм; ℓ
τ
= … мм; τ = … с. N
τ
= ... .
N ℓ, мм t, c T, c A
0
, мм A, мм β, с
-1
Λ
4. Сдвигая измерительную линейку вдоль виброграммы, найти
положение, где амплитуда уменьшилась в е раз (А = A
τ
); отметить
точку с координатой l
τ
относительно места, где была измерена
начальная амплитуда А
0
, и измерить расстояние l
τ
(см. рис. 20.1)
14
.
5. Измерить расстояние l
ms
между метками времени на виброграмме
и определить время релаксации по формуле
τ =
l
τ
l
ms
⋅t
ms
, где t
ms
– вре-
меннóй интервал, соответствующий расстоянию l
ms
между метками
времени на виброграмме (масштаб времени
15
); l
τ
– длина вибро-
граммы, соответствующая времени релаксации (см. п. 4).
13 Так как положение равновесия не отмечено на виброграмме, поэтому для удобства и повы-
шения точности измерений рекомендуется непосредственно измерять не амплитуду, а
размах колебаний – расстояние от верхней огибающей до нижней, измеренное по перпенди-
куляру к линии с метками времени. Такая замена не влияет на результаты вычислений вели-
чин β и Λ, так как в расчётные формулы входит отношение начальной и конечной амплитуд.
14 Расстояние измеряется l
τ
вдоль прямой, параллельной линии с метками времени, от
выбранного места виброграммы, где начальная амплитуда А
0
достаточно велика, до того
места, где амплитуда в е раз меньше, т. е. равна А
τ
= А
0
/е.
15 Масштаб времени указан в паспорте вибрографа. При выполнении работы масштаб t
ms
задаётся преподавателем каждому студенту индивидуально.
26

2.2. Измерение коэффициента затухания
и логарифмического декремента
1. Выбрать на виброграмме не менее трёх участков в различных
местах виброграммы длительностью 2 – 4 колебания и определить
период колебаний для каждого из участков
16
по формуле Т = t/N,
где t – промежуток времени, за который совершается N колебаний.
Выяснить, зависит ли период от времени, и в случае отрицательного
результата найти среднее значение <T>.
2. Для тех же участков виброграммы (см. п. 5) определить
коэффициенты затухания по формуле (20.5) и логарифмические
декременты (20.7). Выяснить характер зависимости этих величин от
времени. Если по данным опытов не обнаруживается изменения
величин β и Λ с учётом погрешностей (±Δβ и ±ΔΛ), найти средние
значения <β> и <Λ>.
3. Вычислить коэффициент затухания β
ф
по формуле (20.2),
исходя из физического смысла величины β. Подсчитать по вибро-
грамме количество колебаний N
τ
за время релаксации и вычислить
логарифмический декремент Λ
ф
по формуле (20.4).
4. Сравнить значения: <β> и β
ф
; <Λ> и Λ
ф
; сделать вывод о
справедливости закона
A= A
0
∙ e
−β⋅t
.
Контрольные вопросы
Допуск
1. Какое колебание называется свободным?
2. Что такое время релаксации?
3. По какому закону зависит от времени амплитуда свободных колебаний?
4. Физический смысл и единица коэффициента затухания.
5. Определение и физический смысл логарифмического декремента
колебания.
Защита
6. Может ли свободное колебание быть гармоническим? Является ли
свободное колебание периодическим движением? Как в данной работе
найти период?
16 Участки выбираются по всей длине виброграммы. Допустимо перекрытие участков, когда
общее число колебаний на виброграмме невелико.
27

7. Как определяется по виброграмме время релаксации?
8. Записать две формулы (с расшифровкой обозначений), используемые в
работе для расчёта коэффициента затухания двумя разными способами по
данным измерений.
9. Какие две формулы вы использовали, чтобы найти двумя разными
способами логарифмический декремент свободных колебаний по резуль-
татам измерений?
10. От каких параметров колебательной системы зависит коэффициент
затухания?
11. При каком условии колебательная система, выведенная из состояния
равновесия, не совершает колебаний?
12. Вывести формулы, применяемые в данной работе для расчёта
характеристик колебательного процесса: а) коэффициента затухания
β =
1
t
⋅ ln
A
0
A
t
; б) логарифмического декремента
=
1
N
⋅ln
A
0
A
t
.
13. Вывести формулу, раскрывающую физический смысл логарифмиче-
ского декремента колебаний,
ф
=
1
N
.
14. *Логарифмический декремент некоторой колебательной системы
составляет 0,010. Период колебаний Т = 1 с. Чему равно время релаксации?
15. *Вывести формулу взаимосвязи логарифмического декремента и
коэффициента затухания: Λ = βТ.
16. *Коэффициент затухания равен 0,40 с
-1
при частоте колебаний 100 Гц.
Можно ли приближённо считать, что частота затухающих колебаний равна
собственной частоте?
17. *Исходя из второго закона Ньютона, вывести дифференциальное
уравнение свободных колебаний груза на пружине в вязкой среде.
18. *Физический смысл коэффициента сопротивления.
28
Лабораторная работа 20э
СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
Рекомендуемая литература
[7]. §3.2.4. С. 270. Свободные колебания в колебательном контуре.
[3]. §5.9.1, 5.9.2. С. 183. Дифференциальное уравнение затухающих
колебаний, его решение. Характеристики, вводимые для описания
затухающих колебаний.
[15]. §146. С. 264. Дифференциальное уравнение свободных
затухающих колебаний (механических и электромагнитных) и его
решение. Автоколебания.
Основы теории
Колебательный контур – это замкнутая цепь, состоящая из после-
довательно соединённых конденсатора и катушки индуктивности.
Контур обладает электроёмкостью С, индуктивностью L и омическим
(активным) сопротивлением R. Последнее включает в себя омическое
сопротивление провода катушки и сопротивление соединительных
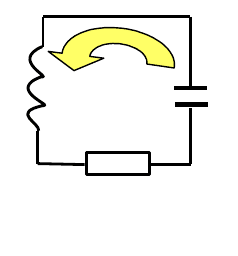
проводов. Схема колебательного контура приведена на рис. 20э.1.
Выясним, как возникают колебания в контуре.
Вначале конденсатор заряжают до некоторой
разности потенциалов на его обкладках U
0
. При
этом конденсатору сообщается заряд Q
0
и соответ-
ственно энергия электрического поля W
эл
= CU
0
2
/2.
Затем конденсатор замыкают на катушку.
Начинается его разрядка и в катушке возникает ток
i, увеличивающийся от нуля до некоторого
максимального значения I
0
. В катушке создаётся
магнитное поле, и энергия электрического поля между обкладками
конденсатора постепенно переходит в энергию магнитного поля. Сила
тока в контуре и энергия магнитного поля в момент полной разрядки
конденсатора достигают своих максимальных значений: I
0
и
W
м
= LI
0
2
/2. В момент полной разрядки конденсатора разность
потенциалов равна нулю и сила тока в цепи, казалось бы, должна
резко упасть до нуля. Однако уменьшению тока в катушке
препятствует ЭДС самоиндукции, поддерживающая ток в прежнем
направлении. Этот ток, убывающий от максимального значения I
0
до
29
L
C
R
Рис. 20э.1.
Колебательный контур
+q
-q
i

нуля, продолжает переносить заряды от одной обкладки конденсатора
к другой в том же направлении и перезаряжает конденсатор.
Перезарядка заканчивается, когда сила тока в контуре становится
равной нулю, равно как и соответствующая энергия магнитного поля.
Энергия колебательной системы полностью сосредотачивается в
электрическом поле конденсатора. В следующий момент конденсатор
начнёт разряжаться, а ток пойдёт в противоположном направлении.
Ток в контуре возрастает, пока конденсатор не разрядится полностью,
а затем убывает, поддерживаемый ЭДС самоиндукции, и снова
перезаряжает конденсатор. В результате колебательная система
возвращается в исходное состояние. На этом завершается один цикл
(период) колебаний в контуре.
Взаимное превращение энергии электрического и магнитного
полей сопровождается диссипацией
17
– потерей энергии на нагревание
соединительных проводников. И если энергия не пополняется извне,
то колебания в контуре затухают – амплитуды колеблющихся величин
Q, U, I постепенно уменьшаются с каждым циклом колебаний. Чем
больше омическое сопротивление контура, тем быстрее в нём
затухают колебания.
Затухающие колебания не являются периодическими, поскольку
максимальное начальное значение колеблющейся величины Q, U или
I, достигаемое в некоторый момент времени, в последующем цикле
колебаний не повторяется (становится меньше). Однако колеблю-
щаяся величина обращается в нуль, достигает максимума и минимума
через равные промежутки времени. Поэтому затухающие колебания
считаются условно периодическими. Они (как и гармонические
колебания) характеризуются периодом Т (условным), частотой ν и
угловой частотой ω = 2πν.
Электрический контур можно считать линейной
18
системой, если
его параметры R, L и C не зависят ни от силы тока в контуре, ни от
напряжения.
Найдём дифференциальное уравнение, описывающее свободные
затухающие колебания в контуре. Воспользуемся законом Ома и
вытекающим из него вторым правилом Кирхгофа, которые
17 Диссипация энергии [dissipatio (лат.) – рассеивание] – переход энергии упорядоченного
движения (например, энергии электрического тока) в энергию хаотического движения
частиц (теплоту).
18 Система называется линейной, если параметры, характеризующие систему, не изменяются в
рассматриваемом процессе. Линейные системы описываются линейными дифференциаль-
ными уравнениями.
30
