Горкунова Т.В., Коробейникова Е.В. Учебно-практическое пособие по математике
Подождите немного. Документ загружается.

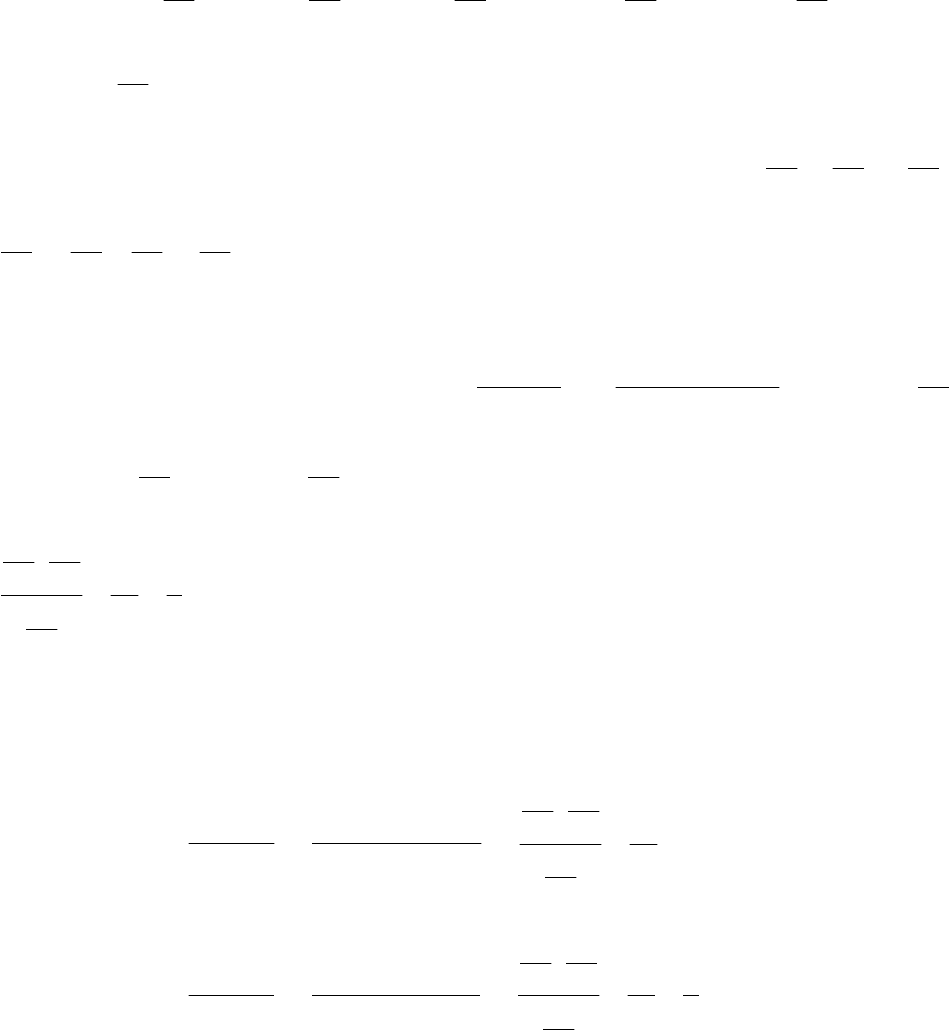
отличника, или если зачетка принадлежит студенту третьей группы и зачетка
отличника.
Поэтому Р(А) = Р(В
1
)Р(А/В
1
) + Р(В
2
)Р(А/В
2
) + Р(В
3
)Р(А/В
3
), так как
произведение событий А и В
i
находится по формуле условной вероятности.
Р(В
1
) =
67
22
, Р(В
2
) =
67
20
, Р(В
3
) =
67
25
. Р(А/В
1
) =
22
5
; Р(А/В
2
) =
20
7
;
Р(А/В
3
) =
25
3
.
Таким образом, по формуле полной вероятности Р(А) =
67
22
·
22
5
+
67
20
·
20
7
+
67
25
·
25
3
=
67
15
.
б) События В
1
, В
2
, В
3
– попарно несовместны.
По формуле Байеса, Р(В
1
/А) =
)(
)(
1
АР
АВР
=
)(
)/()(
11
АР
ВАРВР
. Р(В
1
) =
67
22
,
Р(А/В
1
) =
22
5
, Р(А) =
67
15
(как было найдено ранее), поэтому Р(В
1
/А) =
3
1
15
5
67
15
22
5
67
22
==
⋅
. Аналогичным образом можно найти вероятность события, что
потерянная зачетка отличника принадлежит студенту второй группы и третьей
группы:
Р(В
2
/А) =
)(
)(
2
АР
АВР
=
)(
)/()(
22
АР
ВАРВР
=
15
7
67
15
20
7
67
20
=
⋅
.
Р(В
3
/А) =
)(
)(
3
АР
АВР
=
)(
)/()(
33
АР
ВАРВР
=
5
1
15
3
67
15
25
3
67
25
==
⋅
.

III тип. Комбинаторные задачи на вероятность
Задача. Набирая номер телефона, абонент забыл первые 3 цифры.
Какова вероятность правильного набора абонентом цифр наугад?
Решение
Данную задачу можно разбить на 2 части:
1)
Определить, сколькими способами можно составить трехзначное число
(первые 3 цифры телефона);
2)
Определить вероятность набора абонентом верного номера наугад.
Трехзначное число состоит из трех цифр:
cba . Первую цифру – число
тысячных (множество
a), можно выбрать из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9,
т. е. множество
а = {1, 2, 3, 4, 5, 6, 7, 8, 9},
b = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
c = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Таким образом, задачу можно переформулировать: сколькими способами
(
N) из элементов множеств a, b, c можно составить тройку упорядоченных
элементов? Согласно правилу произведения
N = 9 · 10 · 10= 900.
Из 900 номеров только один является верным, следовательно,
вероятность набора верного номера наугад
Р(А)=1/900.
Ответ: 1/900.
Задача. Написано слово МИР! Буквы (символы) записали на отдельных
карточках и перемешали. Какова вероятность того, что наудачу извлеченные
по порядку буквы снова составят слово МИР!
Решение
Всего имеется 4 карточки: М, И, Р, !. Из них нужно составить
определенное слово из 3 букв и одного знака, т.е. нужно найти количество
перестановок 4 символов по 4 местам. Р
4
= 4! = 24.
При данных перестановках только один вариант расставления
имеющихся символов подойдет по условию. Следовательно, вероятность
наудачу составить нужное слово
Р(А)= 1/24.

Ответ: 1/24.
Задача. В урне лежат 8 занумерованных шаров. Наугад берут 4 шара.
Какова вероятность того, что 3 шара окажутся с нечетными номерами?
Решение
Всего нужно вытащить 4 шара из 8. Это можно сделать 70
4*3*2*1
5*6*7*8
4
8
==C
способами. Из 4 шаров 3 с нечетными номерами можно получить
4
3*2*1
2*3*4
3
4
==C
способами. Значит вероятность того, что если из 8 пронумерованных шаров
извлечь 4 и 3 из них будут с нечетными номерами
Р(А)= 4/70 = 2/35.
Ответ: 2/35.
IV тип. Подсчет количества информации в сообщении
Задача. В пруду 50000 рыб (8000 карасей, 2000 щук, 40000
пескарей).Какое сообщение наиболее информативно: о том, что рыбак поймал
карася, щуку или пескаря?
Решение
Для начала определим вероятность поймать каждую рыбу. Вероятность
поймать карася
Р(А)= 8000/50000 = 4/25 = 0,16. Вероятность поймать щуку
Р(А)= 2000/50000 = 2/50 = 0,04. Вероятность поймать пескаря Р(А)=
40000/50000 = 4/5 = 0,8.
Зная вероятность поймать каждую рыбу, можно определить количество
информации в сообщениях.
Количество информации в сообщении о том, что рыбак поймал карася
I =
log
2
(1/0,16) = log
2
(100/16) = log
2
(6,25) = 2,64. Количество информации в
сообщении о том, что рыбак поймал щуку
I = log
2
(1/0,04) = log
2
(100/4) =
log
2
(25) = 4,64. Количество информации в сообщении о том, что рыбак поймал
пескаря
I = log
2
(1/0,8) = log
2
(10/8) = log
2
(1,25) = 0,32.
На этом основании можно сделать вывод, что наиболее информативно
сообщение о поимке щуки.
Ответ: наиболее информативно сообщение о поимке щуки.
Задача. Определить количество информации в слове МАМА, если по
данным словаря русского языка частота появления символа: М – 0,026; А –
0,062.
Решение
В данной задаче частота появления символов – вероятность их появления,
которую используют при подсчете количества информации. Следовательно,
количество информации в слове МАМА
I = log
2
(1/0.026) + log
2
(1/0.062) +
log
2
(1/0.026) + log
2
(1/0.062) = 2*log
2
(1/0.026) + 2*log
2
(1/0.062) =
2*log
2
(1000/26) + 2*log
2
(1000/62) ~ 2*log
2
(38,46) + 2*log
2
(16,13) = log
2
(38,46)
2
+
log
2
(16,13)
2
~ log
2
(1479) + log
2
(260) = =log
2
(1479 * 260) = log
2
(384540) ~ 18.
Ответ: количество информации в слове МАМА ~ 18 бит.
Задачи для самостоятельного решения
I тип
Задача 107*.
Подбрасывается монета.
а) описать пространство элементарных исходов;
б) указать невозможное и достоверное события для данного опыта;
в) найти исходы, благоприятствующие появлению события А =
«выпадение орла»;
г) найти вероятность наступления события А;
д) найти событие, противоположное событию А и его вероятность.
Задача 108*. В мешке 3 геометрические фигуры – куб, тетраэдр, шар. Из мешка
случайным образом извлекается одна фигура.
а) описать пространство элементарных исходов;
б) указать невозможное и достоверное события для данного опыта;
в) найти исходы, благоприятствующие появлению события А =
«извлечение фигуры без углов»;
г) найти вероятность наступления события А;
д) найти событие, противоположное событию А и его вероятность.
Задача 109*. В лототроне находится 36 шаров. Вслепую извлекается один из
шаров.

а) описать пространство элементарных исходов;
б) указать невозможное и достоверное события для данного опыта;
в) найти исходы, благоприятствующие появлению события
А – номер
шара будет кратным 6;
г) найти вероятность наступления события
А;
д) найти событие, противоположное событию
А и его вероятность.
Задача 110*. А – выпадение на кубике числа кратного 2, В – выпадение на
кубике числа кратного 3. Найти события
А + В и А • В.
Задача 111*. А – извлечение из урны с 36 занумерованными шарами шара с
номером кратным 5,
В – извлечение из урны с 36 занумерованными шарами
шара с номером кратным 7. Найти события
А + В и А • В.
Задача 112*. Опыт заключается в покупке лотерейных билетов. А
1
–
выигрышным оказался первый билет,
А
2
– выигрышным оказался второй билет,
А
3
– выигрышным оказался третий билет. Пусть события независимы. Найти
события
А
1
А
2
А
3
,
321
ААА ,
321
ААА ++
,
313221
А
А
А
А
А
А
+
+
,
2
31
1
32
3
21
ААААААААА ++ .
Задача 113*.
В коробке находится печенье, которое из нее достают. А – первое
печенье оказалось «с сюрпризом»,
В – второе печенье оказалось «с
сюрпризом»,
С – третье печенье оказалось «с сюрпризом». Найти события АВС,
C
A
B
C
B
A
BC
А
+
+
, АВ + ВС + АС.
Задача 114**.
Наудачу выбрано натуральное число, не превосходящее 20.
Какова вероятность того, что число:
а)
кратно 5;
б)
кратно 3;
в)
простое;
г)
составное;
д)
не простое, не составное.
Задача 115**.
В корзине а белых и b черных шаров. Из этой корзины
вынимают один шар и откладывают в сторону. Этот шар оказался белым. После
этого из корзины берут еще один шар. Какова вероятность, что этот шар также
белый?
Задача 116**.
На книжной полке стоят 17 книг, из них 5 детективов, остальные
учебники, какова вероятность того, что сонный студент наудачу возьмет
учебник? Детектив?
Задача 117**. В магазин пришло 26 упаковок шампуня. Из них 18 упаковок
шампуня PantineProV, остальные Head&Shoulders. Какова вероятность того, что
в случайно взятой коробке окажется PantineProV; Head&Shoulders?
Задача 118**.
В ящике письменного стола лежат 15 одинаковых ручек, в
четырех из них черный стержень, в 11 синий. Какова вероятность того, что
стержень синий? Черный?
Задача 119**.
Какова вероятность того, что наудачу из колоды в 36 карт будет
извлечена карта:
а)
красной масти;
б)
валет;
в)
пиковой масти?
Задача 120**.
Какова вероятность того, что из урны с 50 пронумерованными
шарами будет извлечен шар с номером:
а)
четным;
б)
кратным 7;
в)
не кратным 8?
Задача 121***. Горнолыжник несется с горы с очень большой скоростью, но
не знает, что поперек всей трассы прорыта канава (очень широкая, что он не
сможет пролететь через нее). Через канаву проложен мостик. Если лыжник
попадет на мостик, то он останется жив. Найти вероятность того, что лыжник
останется жив. Длина канавы 34 м 40 см, а
мостик уже канавы на 33 м 48 см.
Задача 122***. Какова вероятность, что парашютист не приземлится на
садовый участок, стоящий на посадочном поле, если площадь поля 75 га, а
участка 2 га? Какова вероятность, что приземлится?
Задача 123***. Какова вероятность того, что метеорит упадет в озеро,
находящееся в лесу, если площадь леса 180 га, а площадь озера 4 га? Какова
вероятность того, что метеорит упадет в лес?
Задача 124***. В круг вписан треугольник. Площадь круга 15 см
2
, площадь
треугольника 8 см
2
. Какова вероятность того, что стрелок с первого выстрела
попадет в круг, квадрат?
Задача 125***.
Ученик в диктанте из 21 слова допускает 5 ошибок. Какова
вероятность, что в следующем слове он допустит ошибку? Какова вероятность,
что не допустит ошибку?
Задача 126***. В лотерее из 1000 билетов выигрывает 3. Какова вероятность,
что купленный билет окажется выигрышным? Какова вероятность, что билет
окажется невыигрышным?
Задача 127***. Из 12 выстрелов стрелок промахнулся 2 раза. Какова
вероятность того, что при следующем выстреле он промахнется? Какова
вероятность, что не промахнется?
Задача 128***. Человек, занимающийся статистикой, решил провести
эксперимент. Он 274 раза случайным образом набирал телефонные номера. В
156 случаях к телефону подходили женщины. Какова вероятность того, что при
следующем звонке трубку возьмет мужчина? Какова вероятность,
что женщина?
II тип
Задача 129*.
Какова вероятность случайного выпадения козырного туза или
козырного короля из колоды в 36 карт?
Задача 130*. Какова вероятность выпадения единицы или тройки, или четверки
на игральной кости?
Задача 131*. Вероятность, что студент вытянет билет, из которого он знает два
вопроса, 0,4. Вероятность, что из билета он знает один вопрос, 0,1. Студент
получит положительную оценку, при условии, если ответит хотя бы на один
вопрос в билете. Какова вероятность, что студент получит положительную
оценку? Какова вероятность, что студент получит «неудовлетворительно»?
Задача 132*. Вероятность вытащить из урны шар красного цвета 0,3, белого
цвета 0,4. Кроме этого в урне имеются шары черного цвета. Какова вероятность
вытащить из урны шар черного цвета?
Задача 133*. Два хлебокомбината производят булки с маком и с изюмом. На
пробу экспертам предоставлено 8 булок первого хлебокомбината и 8 – второго.
Из общего числа 7 булок с изюмом, остальные с маком. Какова вероятность
того, что случайно взятая экспертом булка будет булкой с изюмом,
производства первого хлебокомбината?
Задача 134*. В аквариуме 4 золотые рыбки, 7 серебряных, 3 красных. Из них 10
самцов и 4 самки. Какова вероятность того, что наудачу выловленная рыба
окажется золотым самцом?
Задача 135*. У аудиопиратов изъято 80 дисков классической музыки,
записанных в 2004 году, и 76 дисков классической музыки, записанных в 2005
году. Причем в 56 случаях музыка записана на диски CD-RW, а остальная на
CD-R. Какова вероятность того, что случайно взятый диск окажется CD-R 2005
года?
Задача 136*. В магазине для садоводов имеется 12 пакетиков семян моркови и
14 пакетиков семян свеклы. Из них 7 пакетиков производства Голландии, 19 –
производства России. Какова вероятность того, что в случайно взятом пакетике
окажутся семена моркови производства России?
Задача 137**. Вероятность, что отец купит булку хлеба 0,8, дочь – 0,5. Какова
вероятность, что хотя бы один из них купит хлеб?
Задача 138**. Одна подруга опоздает на практическое занятие с вероятностью
1/3, вторая – 4/5. Какова вероятность, что опоздает хотя бы одна подруга?
Задача 139**. Вероятность, что одному ученику удастся списать контрольную
работу 3/5, другому – 2/3. Какова вероятность, что спишет решение хотя бы
один ученик?
Задача 140**. Вероятность того, что первый стрелок попадет в цель – 0,56,
вероятность того, что второй стрелок попадет в цель – 0,43. Какова вероятность
того, что хотя бы один стрелок попадет в цель?
Задача 141**. Из 29 билетов 13 – счастливые. Какова вероятность, что первый
студент вытянет счастливый билет, и второй следом за ним вытянет
счастливый? Какова вероятность, что первый студент вытянет несчастливый
билет, а второй счастливый? Какова вероятность, что оба студента вытянут
несчастливые билеты?
Задача 142**. В подгруппе 5 юношей, 7 девушек. Какова вероятность, что
наудачу выбранные тетради будут принадлежать двум девушкам? Первая
тетрадь принадлежит юноше, вторая девушке? Первая девушке, вторая юноше?
Обе тетради принадлежат юношам?
Задача 143**.
На карточках написаны 33 буквы русского алфавита. Какова
вероятность, что из двух наугад выбранных карточек обе будут гласными? Обе
согласными?
Задача 144**.
В урне 10 пронумерованных шаров. Какова вероятность того,
что из двух, наугад выбранных шаров, номера у обоих будут четными?
Задача 145***. В зоопарке 3 вольера с обезьянами: в первом живут 3 обезьяны,
во втором – 2, в третьем – 6. Для профилактики их всех должен осмотреть врач.
а)
Какова вероятность того, что первым на прием к врачу попадет самец,
если в первом и втором вольере по одному самцу, а в третьем – 2?
б) Найти вероятность того, что самец, первым попавший к врачу,
окажется из первого, второго, третьего вольера?
Задача 146***.
На соревнования прибыло 22 бегуна, 15 пловцов, 7
фехтовальщиков. Для соревнований каждый спортсмен заполнил специальную
карточку, в которой указал информацию о себе.
а)
Какова вероятность того, что случайно взятая карточка принадлежит
спортсмену из США, если из США прибыло 12 спортсменов, из Англии – 18, из
Франции – 14?
б)
Какова вероятность того, что карточка спортсмена из США
принадлежит пловцу, бегуну, фехтовальщику?
Задача 147***. По шоссе проехало 100 машин: 52 – Жигули, 22 – Лада, 26 –
Мерседес. Причем из этих 100 машин 46 заправлялись на автозаправке Лукойл,
38 – Спартак, 16 – Сибнефть.
а)
Какова вероятность того, что случайно остановленная на шоссе машина
окажется Мерседесом?
б) Какова вероятность того, что случайно остановленный на шоссе
Мерседес воспользовался автозаправкой Лукойл, Спартак, Сибнефть?
Задача 148***.
На складе находится 15 упаковок туалетной воды, 4 упаковки
духов и 8 упаковок ароматизированных масел. Из всего этого количества 7
упаковок произведено фирмой Oriflame, 9 – Avon, 11 – Faberlic.
а)
Какова вероятность того, что случайно взятая упаковка будет с
ароматизированным маслом?
б)
Какова вероятность того, что случайно взятая упаковка
ароматизированного масла будет производства Oriflame, Avon, Faberlic?
III тип
Задача 149*.
На отдельных карточках написаны буквы К, М, П, Т, Р, О, Ю, Ь.
Карточки перемешивают и начинают извлекать по одной, составляя слово.
Какова вероятность того, что по порядку извлеченные карточки образуют слово
КОМПЬЮТЕР?
Задача 150*. Какова вероятность того, что обезьяна, постучав по клавиатуре,
состоящей из 105 клавиш, 7 раз напечатает семибуквенное слово?
Задача 151*. Имеются 3 пронумерованные урны. Какова вероятность
случайным образом разместить 4 одинаковых шара в первую урну?
Задача 152*. Имеются карточки с тремя буквами О, двумя – К и двумя – Л.
Какова вероятность составить случайным образом из карточек с этими буквами
слово КОЛОКОЛ.
