Горкунова Т.В., Коробейникова Е.В. Учебно-практическое пособие по математике
Подождите немного. Документ загружается.


наступление одного из них исключает возможность наступления другого.
Говорят, что событие В следует из события А, если событие В происходит
всегда, когда произошло событие А. Два события А и В называются равными,
если из А следует В и из В следует А. События называются независимыми, если
появление одного события не влечет
появление другого.
События A
1
, A
2
, ..., A
n
образуют полную группу событий, если хотя бы
одно из них непременно должно произойти (при каждом осуществлении
комплекса условий).
Суммой двух событий А и В называется событие А + В, состоящее в том,
что произошло событие А
или событие В.
Произведением двух событий А и В называется событие АВ,
заключающееся в совместном наступлении событий А
и В.
Основные свойства сложения и произведения событий
Пусть А, В – некоторые события, тогда:
1.
А + В; АВ вновь являются событиями.
2.
А + В = В + А; АВ = ВА (коммутативный закон).
3.
А + (В + С) =( А + В) + С; А(ВС) =(АВ)С (ассоциативный закон).
4.
Из события А следует сумма этого события с любым событием В:
А
⊂
А + В.
5.
Из события АВ следуют событие А и событие В:
АВ
⊂
А, АВ
⊂
В.
А(В + С) = АВ + АС (дистрибутивный закон).
Классическое определение вероятности. Пусть некоторый опыт имеет n
равновозможных и несовместных исходов. Вероятностью Р(А) события А
называется отношение числа благоприятных исходов m(А) к общему числу n
несовместных равновозможных исходов:
Р (А) =
n
Аm )(
.

Свойства вероятности
1. Для любого случайного события 0
≤
Р(А)
≤
1.
2.
Пусть А
1
, А
2
, А
3
,…, А
k
– все события, которые могут произойти в
результате опыта. Тогда 1)(...)()()(
321
=
+
+
+
+
k
A
P
A
P
A
P
A
P
.
3.
Пусть А – некоторое событие, тогда верно равенство Р(А) + Р(
А
) = 1.
Правило суммы вероятностей. Вероятность суммы несовместных
событий есть сумма вероятностей этих событий: Р(А + В) = Р(А) + Р(В).
Правило произведения вероятностей независимых событий.
Вероятность произведения событий есть произведение вероятностей этих
событий: Р(А • В) = Р(А) • Р(В).
События А и В называются зависимыми, если появление одного из них
изменяет вероятность появления другого.
Условной вероятностью Р(В/А) называется вероятность события В,
вычисленная в предположении, что событие А уже произошло.
Правило произведения вероятностей зависимых событий.
Вероятность произведения двух зависимых событий А и В равна произведению
вероятности одного из них на условную вероятность другого, в предположении,
что первое уже произошло, т.е. Р(АВ)= Р(А) • Р(В/А).
Вероятность суммы совместных событий.
Вероятность суммы
совместных событий есть сумма вероятностей этих событий без вероятности из
совместного наступления: Р(А + В) = Р(А) + Р(В) – Р(А • В).
Формула полной вероятности. Пусть B
1
, B
2
, …, B
n
– полная система
несовместных событий.
Р(А) = Р(В
1
)Р(А/В
1
) + Р(В
2
)Р(А/В
2
) + … + Р(В
n
)Р(А/В
n
) =
∑
=
n
k
kk
BAPВР
1
)/()(.
Формула Байеса:
Р(В
k
/А) =
∑
=
=
n
k
kk
кkкk
BAPВР
ВАРВР
АР
ВАРВР
1
)/()(
)/()(
)(
)/()(
.
Пусть в результате некоторого случайного испытания может произойти
или не произойти определенное событие А. Если событие произошло,

испытание называется успешным, а событие – успехом. Испытание повторяется
n раз. При этом соблюдаются следующие условия:
вероятность успеха Р(А) = р в каждом испытании одна и та же;
результат любого испытания не зависит от исходов предыдущих
испытаний.
Противоположное событие
А
событию А называется неудача, и его
вероятность обозначается q, причем q = 1 – р, так как в данной схеме
подразумевается, что опыт может иметь только два исхода: успех или неудача.
Такая последовательность испытаний с двумя исходами (успех/неудача)
называется последовательностью независимых испытаний Бернулли или
схемой Бернулли. Вероятность того, что в схеме Бернулли
из n независимых
испытаний произошло ровно k успехов, находится по формуле Бернулли:
knkk
nn
qpCkР
−
=)( .
Следствия из формулы Бернулли
1.
n
pnР
n
=)(,
n
qР
n
=)0(.
2.
P
n
(0) + P
n
(1) + P
n
(2) + … + P
n
(n) = 1.
Предельная теорема Пуассона
Рассмотрим случай, когда вероятность р наступления некоторого события
А достаточно малая величина. Например, рождение близнецов, достижение
столетнего возраста, опечатка в книге и т. д. По формуле Бернулли
knkk
nn
qpCkР
−
=)( . В рассматриваемом случае n → ∞, а р → 0. Пусть величина λ
= np остается ограниченной: λ < const, k – фиксировано. При указанных
условиях справедлива теорема Пуассона )(
k
Р
n
≈
λ
λ
−
e
k
k
!
.
Пользуясь теоремой Пуассона, мы можем при определенных условиях
заменять вероятность P
n
(k) приближенно равным ей выражением
λ
λ
−
e
k
k
!
. Для
данного выражения составлены таблицы, с их помощью можно для заданных k

и λ найти соответствующее число
λ
λ
−
e
k
k
!
. Число λ = np – среднее число
успехов.
Геометрическое определение вероятности. Пространство
элементарных исходов Ω – произвольное конечное множество на прямой,
плоскости или n-мерном арифметическом пространстве. События –
всевозможные измеримые подмножества А множества Ω. Вероятность события
А – отношение лебеговой меры множества А и пространства элементарных
исходов: Р(А) =
)(
)(
Ω
μ
μ
А
.
Лебегова мера множества – это обобщение понятия длины отрезка,
площади фигуры, объема тела. Например, для плоскости геометрическое
определение вероятности будет выглядеть следующим образом.
Пусть D – некоторая конечная область плоскости. В эту область
бросается точка, причем попадание ее в любую точку области D считается
равновероятным. Тогда геометрической вероятностью попадания точки в
любую область
D
1
, лежащую в D, назовем отношение площади области D
1
к
площади области D. P(D
1
) =
S(D)
)S(D
1
, где S(D
1
), S(D) – соответственно площади
областей D
1
, D.
Статистическое определение вероятности. Пусть А – случайное
событие по отношению к некоторому опыту. Предположим, что опыт
произведен N раз и при этом событие А наступило в N
A
случаях. Отношение
N
N
A
=
ν
называется частотой наступления события А в рассматриваемой
серии опыта. С увеличением числа опытов частота стабилизируется,
приближается к некоторой постоянной
р(А).
Определение. Статистической вероятностью случайного события р(А)
называют связанное с данным событием постоянное число, вокруг которого
колеблется частота наступления этого события в длинных сериях опытов.

Количество информации
Количественная зависимость между вероятностью события (P) и
количеством информации в сообщении о нем (
I) выражается формулой:
I = log
2
(
P
1
) = – log
2
P.
Практические задания
Примеры решений
I тип.
Общие понятия теории вероятности. Классическая вероятность.
Геометрическая и статистическая вероятность
Задача. Подкидывается игральный кубик.
а) описать пространство элементарных исходов;
б) указать невозможное и достоверное события для данного опыта;
в) найти исходы, благоприятствующие появлению события А – выпало
четное число;
г) найти вероятность наступления события А;
д) найти событие, противоположное событию А и его вероятность.
Решение
а) В данном опыте возможны следующие исходы: «выпадение 1»,
«выпадение 2», «выпадение 3», «выпадение 4», «выпадение 5», «выпадение 6»,
т. е. пространство элементарных исходов – это множество {1, 2, 3, 4, 5, 6}.
б) Невозможным событием для данного опыта является, например,
выпадение семерки. Достоверным событием является событие
А – выпадение
одного из шести очков: 1 или 2, или 3, или 4, или 5, или 6.
в) Событие
А – выпало четное число, означает, что выпало 2 или 4, или 6,
то есть исходами, благоприятствующими событию
А, будут {2, 4, 6}.
г) Число благоприятствующих исходов для события
А три, всего исходов
6, следовательно, по классическому определению вероятности
Р(А) =
2
1
6
3
= .
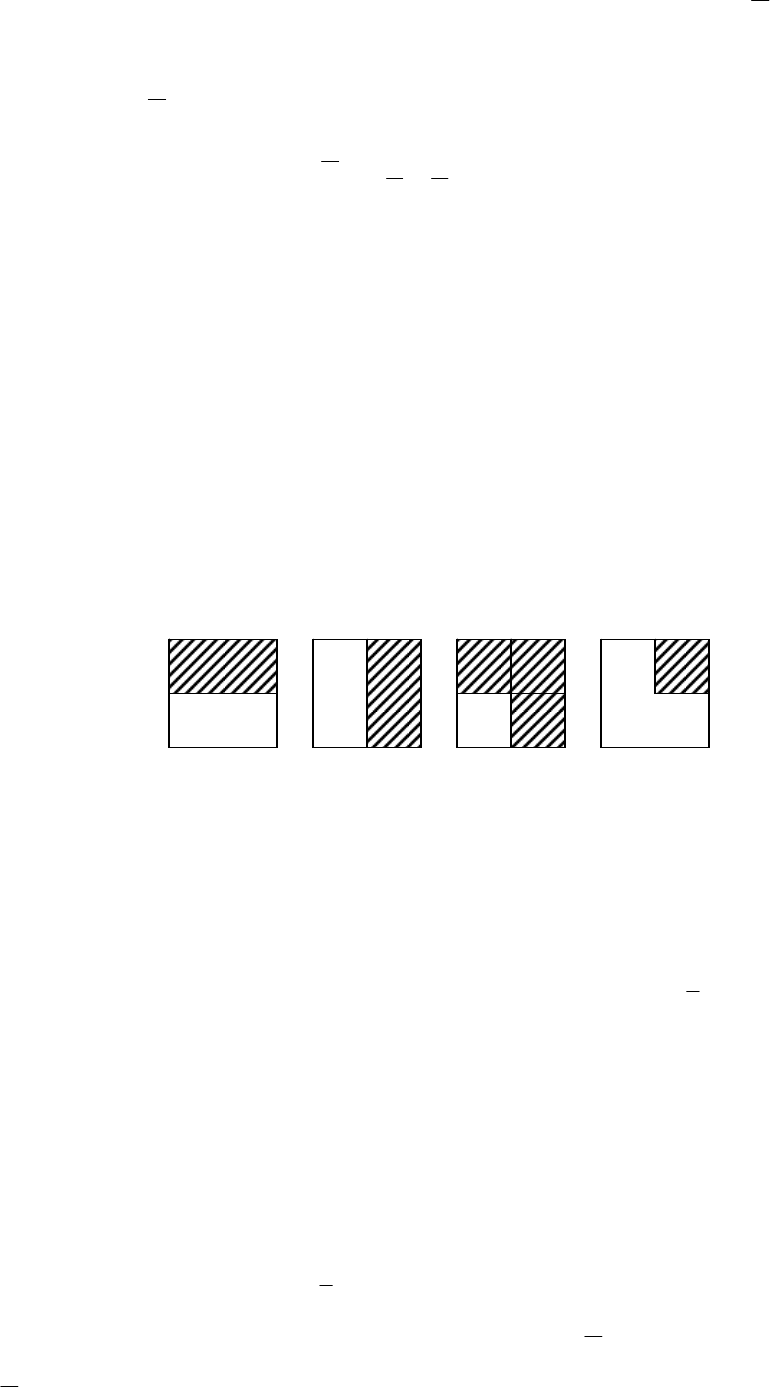
д) Событие, противоположное событию А, есть событие
А
– не выпало
четное число, т. е. выпало нечетное число. Число благоприятствующих исходов
для события
А
три {1, 3, 5}, всего исходов 6, итак, по классическому
определению вероятности Р(
А
) =
2
1
6
3
=
.
Задача. Опыт заключается в том, что на квадратный лист случайным
образом кидается шарик. Пусть А – шарик попадает в верхнюю часть листа,
В – шарик попадает в правую часть листа.
Найти события А + В и А • В.
Решение
Событие А + В – шарик попадает в верхнюю или в правую часть листа.
Событие А
• В – шарик попадает в правую верхнюю четверть листа.
Графически это можно изобразить следующим образом (см. рис.):
Задача. На 33 карточках написаны буквы русского алфавита. Какова
вероятность, что на случайно извлеченной карточке будет гласная буква (А),
согласная (В), ни гласная и ни согласная буква (С)? Какова вероятность
, что
на случайно извлеченной карточке не будет гласная буква (
А
),
Решение
Общее число исходов 33. Исходов, благоприятствующих событию А,
десять (все гласные буквы), событию В – двадцать один (все согласные буквы),
событию С – два (твердый и мягкий знаки). Итак, по классическому
определению вероятности: Р(А) = 10/33, Р(В) = 21/33, Р(С) = 2/33.
Вероятность события
А
– на карточке не будет гласной буквы, можно
найти, опираясь на свойство вероятности Р(А) + Р(
А
) = 1, то есть
Р(
А
) = 1 – Р(А) = 1 – 10/33 = 23/33.
А В А + В
А•В
Ответ: Р(А) = 10/33, Р(В) = 21/33, Р(С) = 2/33, Р(
А
) = 23/33.
Задача. Радиус мишени 10 см. Какова вероятность, что стрелок попадет
в область от 10 до 7, если круги мишени отстоят друг от друга на 1 см?
Решение
Задача на геометрическое определение вероятности.
Пространство элементарных исходов Ω – вся область мишени, ее
площадь вычисляется по формуле площади круга S = πR
2
= π • 10
2
= 100 π.
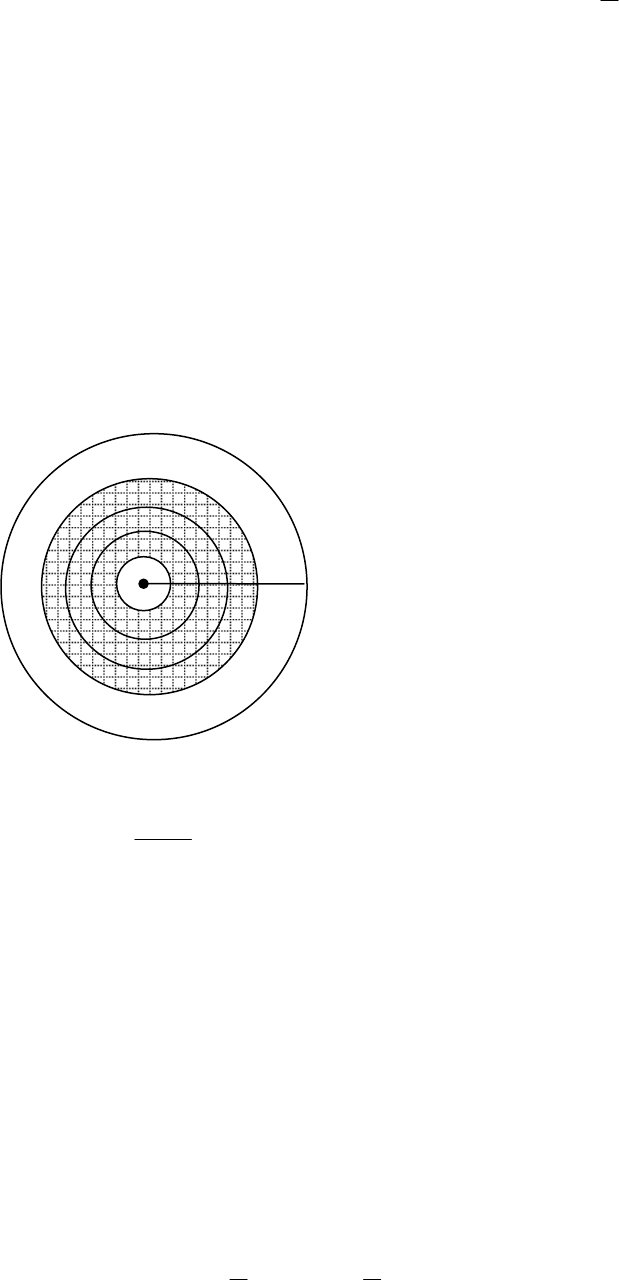
Благоприятствующей областью для искомого события будет круг
радиусом 4 см (см. рис.).
S
1
= πR
1
2
= π • 4
2
= 16 π. Итак, по геометрическому определению
вероятности P =
=
π
π
100
16
0,16.
Ответ: 0,16.
Задача. В течение 100 лет у нескольких поколений одной семьи на 35
случаев рождения детей в 7 случаях рождались двойняшки. Какова
вероятность, что в следующий раз у представителя данной семьи родятся
двойняшки? Не родятся двойняшки?
Решение
Частота появления события колеблется около 7/35. По статистическому
определению, вероятность появления двойняшек Р(А) = 7/35. Вероятность не
появления
двойняшек Р(
А
) = 1 – Р(
А
) = 1 – 7/35 = 28/35.
Ответ: 7/35; 28/35.
1см. 1см. 1см.
1см.
10
9
8
7
…

II тип. Правила суммы и произведения вероятностей. Формулы полной
вероятности и Байеса
Задача. 20 билетов студент знает полностью, в 10 билетах он не знает
по одному из двух вопросов; 7 билетов он не знает вообще. Считается, что
студент получит положительную оценку, когда ответит хотя бы на один из
двух вопросов в билете. Какова вероятность того, что студент получит
положительную оценку?
Решение
Событие А – студент вытягивает
билет, который знает; Р(А)=20/37.
В – вытягивает билет, который он знает наполовину; Р(В)=10/37.
А + В – вытягивает билет, который он знает наполовину или который он
знает полностью. А и В – несовместные события, так как студент не может
одновременно вытянуть билет, который знает и который знает наполовину,
следовательно, Р(А + В) = Р
(А) + Р(В) = 20/37+10/37.
Задача. Один брат выучил 12 билетов из 25, другой – 15. Какова
вероятность, что экзамен сдаст хотя бы один брат?
Решение
Пусть А – первый брат сдаст экзамен. В – второй брат сдаст экзамен.
Искомое событие С = А + В, так как сдача экзамена хотя бы одним братом
означает, что сдает первый или второй
(то есть имеем дело с суммой событий).
События совместны, так как сдать экзамен могут и оба вместе. Применим
формулу для подсчета вероятности суммы совместных событий: Р(А + В) =
Р(А) + Р(В) – Р(А • В). Р(А) = 12/25, Р(В) = 15/25 = 3/5. События А и В
независимы, следовательно, Р(А • В) = Р(
А) • Р(В) = 12/25 • 3/5 = 36/125.
Р(А + В) = 12/25 + 15/25 + 36/125 = 99/125.
Ответ: 99/125.
Задача. Вероятность того, что один студент вытянет счастливый
билет (событие А) 0,45, для другого студента – 0,55 (В). Найти вероятность,
что, сдавая экзамен в разные дни (А, В – независимые): оба студента вытянут
счастливые билеты (С), один из студентов вытянет счастливый билет (D), ни
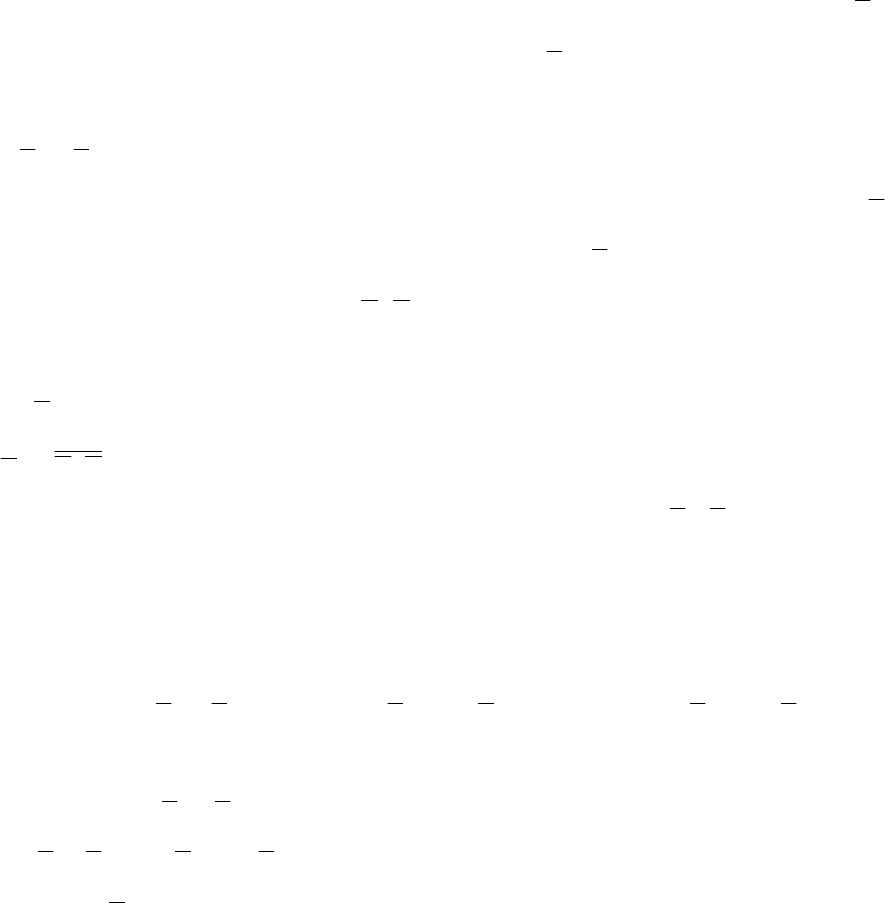
один из них не вытянет счастливый билет (Е), хотя бы один вытянет
счастливый билет (F).
Решение
Представим события С, D, E, F через события А и В.
Событие С – оба вытянут счастливые билеты состоит из событий А –
первый студент вытянет счастливый билет и В – второй студент вытянет
счастливый билет, т. е.
С = А • В.
Событие D – один из студентов вытянет счастливый билет состоит из
следующих событий: А – первый студент вытянет счастливый билет
и
В
–
второй студент не вытянет счастливый билет
или А – второй студент вытянет
счастливый билет
и В – первый студент не вытянет счастливый билет. То есть,
D = А •
В
+ А • В.
Событие Е – ни один не вытянет счастливый билет, состоит из событий
А
– первый студент не вытянет счастливый билет
и
В
– второй студент не
вытянет счастливый билет, т. е. E =
В
А
⋅
.
Событие F – хотя бы один не вытянет счастливый билет, состоит из
события
E
– неверно, что ни один не вытянет счастливый билет, т.
е. F =
E
=
В
А
⋅
.
События А и В независимы, следовательно, и события
В
, А независимы.
При подсчете вероятности событий можно применять правило произведения
независимых событий.
Р(С) = Р(А • В) = Р(А) • Р(В) = 0,45 • 0,55 = 0,2475.
Р(D) = Р(А •
В
+ А • В) = Р(А •
В
) + Р( А • В) = Р(А) • Р(
В
) + Р( А ) • Р(В)
= Р(А) • (1 – Р(В)) + (1 – Р(А))• Р(В)= 0,45 • 0,45 + 0,55 • 0,55 = 0,2025 + 0,3025 =
0,505 (События А •
В
и А • В несовместны).
Р(Е) = Р(
А
•
В
) = Р(
А
) • Р(
В
) = (1 – Р(В)) • (1 – Р(А)) = 0,55 • 0,45 = 0,2475.
Р(F) = P(
E
) = 1 – P(E) = 1 – 0,2475 = 0, 7525.
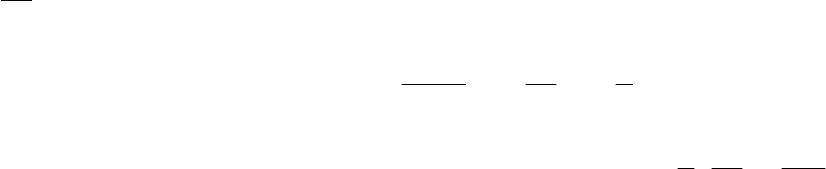
Задача. Из 29 билетов 13 – счастливые. Какова вероятность того, что
первый студент вытянет счастливый билет, а второй следом за ним
несчастливый?
Решение
Пусть В – первый студент вытянул счастливый билет, А – второй студент
вытянул несчастливый билет. Тогда событие А•В – первый студент вытянул
счастливый билет, а второй – несчастливый. А и В – зависимые события
. Р(В) =
29
13
, при условии, что первый билет был счастливый, вероятность вытянуть
несчастливый билет Р(А/В) =
129
16
−
=
28
16
=
7
4
. Тогда по формуле для
произведения зависимых событий Р(АВ) = Р(А/В)Р(В) =
⋅
7
4
29
13
=
203
52
.
Задача. В аудитории занимались 3 группы. В первой группе 5 отличников,
во второй – 7, в третьей – 3.
а) Какова вероятность, что случайно оставленная зачетка принадлежит
отличнику, если в первой группе 22 студента, во второй – 20, в третьей – 25?
б) Найти вероятность того, что потерянная зачетка отличника
принадлежит студенту первой группы? Второй группы? Третьей группы?
Решение
а
) Очевидно, что вероятность искомого события будет изменяться в
зависимости от того, студент какой группы потерял зачетку.
Пусть А – оставленная зачетка принадлежит отличнику, В
1
– зачетка
принадлежит студенту первой группы, В
2
– зачетка принадлежит студенту
второй группы, В
3
– зачетка принадлежит студенту третьей группы.
В
1
, В
2
, В
3
– независимые события. События А/В
1
, А/В
2
, А/В
3
означают, что
зачетка принадлежит отличнику, при условии, что зачетка принадлежит
студенту первой, второй, третьей группы соответственно. Следовательно,
событие А = А
· В
1
+ А · В
2
+ А · В
3
, что означает, что событие А наступит в
случае, если зачетка принадлежит студенту первой группы и зачетка
отличника, или если зачетка принадлежит студенту второй группы и зачетка
