Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§3.10. Логарифмические оценки хроматического числа

241

Отсюда минимальная мощность сигнатуры \Uum(Q(2, fc))|

графа Q(2, fc) равна:

1 при к — 0,

3 • 1 + 3 • 2° - 1 при fc = 1,

3 ■ (3 • 1 + 3 • 2° - 1) + 3 ■ 21 - 1 при fc = 2,

3 • (3 • (3 • 1 + 3 • 2° - 1) + 3 • 21 - 1) + 3 • 22 - 1 при fc = 3,

3 • (3 • (3 • (3.. .3 ■ (3 • 1 + 3 ■ 2° - 1) + 3 • 21 - 1) +

----------V ----------/

fc—1 скобка

+ з ^ - ^ + .-.+ з-г^ -^ + з-г * -1- ! при fc = fc.

Последовательно упрощая выражение для \UMI/l„(Q(2, fc))j, по

лучаем

\UM«H(Q(2, fc))| = 3* + 3* • 2° - 3*-1 + З*"1 • 21 - З*-2 + Зк~2 • 22 -

к к- 1

_ з*-з + # _ + 31 . 2к~1 - з0 = 3* + 5 2 3‘ • 2*“‘ - 5 2 3’ =

1=1 «=о

= 3* + 3 • (3* - 2*) - 0,5 • (3* - 1),

2|C W Q (2, fc))| = 7 • 3* - 6 ■ 2* + 1. (3.37)

Квазиполный граф Q(p, fc), обладающий рассматриваемыми

экстремальными свойствами, получается суммированием квази

полного графа Q(2, fc) и полного графа плотности р — 2:

Q(2, k) + Q (p -2, 0) = Q(p, fc). (3.38)

Обобщением (3.38) является следующая теорема.

Теорема 3.49. Сумма квазиполных графов является квази

полным графом: . .

52Qi(Pi, ki)= q п г > , 5 2 ь ) ■ (3.39)

Согласно (3.38) минимальная мощность носителя квазипол

ного графа Q(p, fc) есть

|Vmin(Q(p, fc))|=3- (2* - 1 )+ р. (3.40)

Минимальная мощность сигнатуры Q(p, fc) представляет собой

сумму минимальной мощности сигнатуры графа Q(2, fc) и мини

мальной мощности сигнатуры полного графа плотности р — 2, ка

ждая вершина которого конусирует граф Q(2, fc). Согласно (3.36)

и (3.37) имеем

\Umin(Q(p, fc))| = 0,5 • (7 • 3* - 6 ■ 2* + 1) +

+ 0,5 • (р — 2) • (р — 3) + (р — 2) • (3 ■ 2* — 1).

242

Гл. 3. Теория графов и мографов

Окончательно получаем

2 \Umin(Q(p, ^))| = 7 • 3fc + 6 • 2fc • (р — 3) + (р — З)2 — р + 2.

(3.41)

Согласно (3.40) любой квазиполный граф первого порядка,

имеющий плотность р, содержит не менее р + 3 вершин. Граф

Q(p, 1), имеющий ровно р + 3 вершин, является суммой цикла

длины 5 и полного графа с плотностью р — 2:

Q(p, 1) = Q{2, 1) +Q {P ~ 2, 0).

Соотношения (3.40) и (3.41) справедливы для любых квазипол

ных графов, имеющих плотность 2 или 3, и для неразложимых

по аддитивной операции “сумма”

квазиполных графов. Структура этих

графов была рассмотрена выше. Для

разложимых квазиполных графов, у

которых по теореме 3.49 плотность не

меньше 4 и хотя бы у двух слагаемых

к{ > 0, эти формулы неверны. На

пример, квазиполный граф Q(4, 2),

являющийся суммой двух графов

<2а(2,1)и<2ь(2,1) (рис. 3.59), Q (4,2) =

= Qa(2, 1) + Qb(2, 1), имеет мощность

Рис. 3.59 носителя, равную 10, и мощность сиг

натуры, равную 35, в то время как ми

нимальные мощности носителя и сигнатуры неразложимого ква

зиполного графа Q(4, 2) равны соответственно 13 и 43 (согласно

(3.40) и (3.41)).

Теорема 3.50. Хроматическое число h(G) графа G равно

его квазиплотности q(G):

h(G) = q(G). (3.42)

Согласно определению квазиполного графа

h(G) > q(G).

Докажем, что в данном соотношении всегда имеет место равен

ство.

Выделим все иевключаемые квазиполные графы, т. е. графы,

для каждого Q,• из которых не найдется квазиполного графа Qa

такого, что Qi С С Qa- Согласно (3.25) среди выделенных подгра

фов имеется хотя бы один, для раскраски которого необходимо q

красок. Покажем, что для минимальной раскраски остальной ча

сти G \Q достаточно тех же q красок. Действительно, если для

минимальной раскраски подграфа G \Q потребуется хотя бы еще

одна новая краска, (д + 1)-я, то это означает, что в подграфе G \Q

существуют замещающий и замыкающий слои, что приводит к

§3.10. Логарифмические оценки хроматического числа

243

образованию квазиполного графа квазиплохносхи д + 1. Последнее

противоречих соохношению (3.25).

Используя формулы (3.40)-(3.42) для графов G; с плотностью

p{Gi) < 4 и для графов, которые не содержат квазиполные под

графы, разложимые по операции “сумма”, можно предложить ло

гарифмические оценки хроматического числа. Имеем

h(G) = q(G) = шах (p(Qi) + k(Qi)) < maxp(Q,) + maxfc(Q,),

(3.43a)

h(G) < p{Qi) + max fc(Q,-), Qi С G, G = {V, U). (3.436)

Согласно (3.40)

Охсюда

maxk(Qi) <

h(G) < p(G) +

(3.44)

В выражении (3.41) 6 • 2k ■ (p - 3) + (p - 3)2 - p + 2 > 0 при

любом k; поэхому

2 \U\

2\U\

maxfc(Q,) < log3

следовательно,

KG) < p[G) + log3

При p(G) = 3 имеем

h(G) < 3 +

l°g3

P(G) > 4;

, p[G) > 4.

2 \U\ + 1

(3.45a)

(3.456)

При p(G) = 2 выражение (3.33) принимает вид

2\UminQ{2, k)| = 7 • 3* - 6 • 2* + 1 > 7 • 3* - 6 • 3* + 1 = 3* + 1;

поэхому

maxfc(Qj) < ]log3 (2|t7| - 1)[.

Охсюда при p(G) = 2 получаем

h{G) < 2 + ]log3 (2|t7| — 1)[. (3.45b)

Согласно схрукхуре квазиполного графа Q(p, к) схепень s(vi)

каждой вершины и,- этого графа удовлехворяех неравенсхву

*(«•■) > 9(G) - 1 = p + k - 1. (3.46)

244

Гл. 3. Теория графов и мографов

h(G) < +1 , GCG,

(3.48)

Тогда по формуле (3.40) мощность сигнатуры \U{Q(p, fc))| нераз

ложимого квазиполного графа удовлетворяет неравенству

\U(Q(p, к))| > 0,5 ■ (3 • (2* - 1) + р) ■ (р + к - 1). (3.47)

Эта оценка достигается для полных графов, когда к = 0.

Согласно (3.40), (3.43а) и (3.47)

2 ■ \Щ&)\

где подграф G удовлетворяет всем неравенствам системы

И<5)|>з -(2*-1) + р (5),

2 \U(G)\ > 7 • 3* = б • 2* • (p(G) - 3) + (p(G) - 3)2 - p(G) + 2,

s(vi) > p{G) + к - l, v ie d ,

(3.49)

т. e. по своим ресурсам, как вершинному, так и реберному, и по ло

кальной топологии (степеням вершин) подграф G может включать

квазиполный граф Q(p, к), где

к =

log;

Очевидно, что

2 ■ [t/(Q)|

И б ) |

(

П С )-Р (С )

♦О

(3.50)

VW « v {8>

— ]всредн(С)[.

Отсюда имеем верхнюю оценку хроматического числа h(G) гра

фа G:

а д < к р е д „ ( < 5 ) [ + 1, (3.51)

где граф G С G удовлетворяет системе неравенств (3.49). Оценка

(3.51) является более эффективной, чем ранее приведенные оценки

Брукса h(G) < sMaKC(G) + 1 и (для определенного класса графов)

h(G) < W c ( G ) .

Как композицию оценок (3.44), (3.45) и (3.51) получаем оценки

хроматического числа h(G) графа G = (V, U):

при p(G) > 4

Цв) < mi„ (р(0) + Jlog2 (lV(6)l3~P(5) + l) [,

P(G) + ]lofo2 > ( 6)l

*средн

(3.52a)

§ 3.10. Логарифмические оценки хроматического числа

245

при p(G) = 3

ц о ) < ^ ( н о н } с ъ ( Щ * ё > + 1)

* « ± i [ . ] w a j

P(G) +

при p(G) = 2

h(G) < min ^

log3

+ 1^; (3.526)

2 +

log:

+ l)[,

2 +

log3(2.|tf(G)|-l)[, [^средиСС) + l ) . (3.52в)

Для вычисления оценки хроматического числа h(G) графа G

на основании формулы (3.51) находим плотность p(G) графа G и,

уменьшая р от p(G) до 2 с шагом 1, по формуле (3.50) находим

к для каждого из этих значений. Максимальная сумма р и соот

ветствующего значения fc, для которых выполняются неравенства

системы (3.49), согласно (3.43а) определяет верхнюю оценку хро

матического числа h(G). Если оцениваемый граф является квази

полным или вычисленная верхняя оценка совпадает с нижней, то

она равна хроматическому числу.

Нижняя оценка хроматического числа

h{G) > p{G) (3.53)

минорируется, как показано Майерсом и Лином, оценкой Геллера

i m i 2

h{G) >

L|V4G)f-2|tf(G)|.

где [ ] — ближайшее целое число, или

h(G) >

|V(g)l

\V(G)\ *средн(^)

(3.54)

(3.55)

Оценки хроматического числа (3.44), (3.45), (3.51), (3.52) ми-

норируют известные верхние оценки h(G).

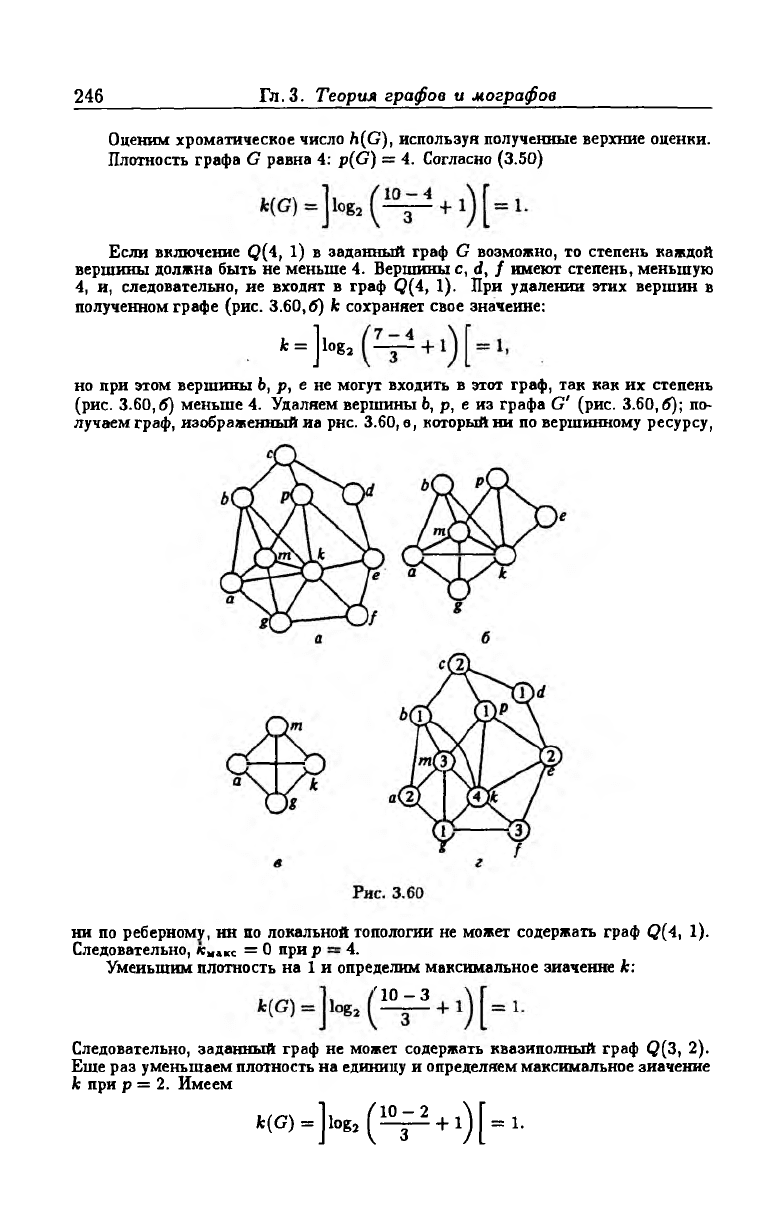
Пример 3.19. Рассмотрим граф G = (V, U) (рнс. 3.60,а).

По оценкам Брукса и Геллера его хроматическое число h(G) заключено в

отрезке [2, 7]:

Г \ПО)\2 1 = Г 1Q2 1 =

L|V(G)|2 — 2|l7(G )|J L 102 — 2 • 20J

*„«.(<?) = 7, 2 < h(G) < 7.

246

Di.3. Теория графов и мографов

Оценим хроматическое число h(G), используя полученные верхние оценки.

Плотность графа G равна 4: p(G) = 4. Согласно (3.50)

Бели включение Q(i, 1) в заданный граф G возможно, то степень каждой

вершины должна быть не меньше 4. Вершины с, d, / имеют степень, меньшую

4, и, следовательно, ие входят в граф Q(4, 1). При удалении этих вершин в

полученном графе (рис. 3.60, б) к сохраняет свое значение:

k= ]i°s*

но при этом вершины Ь, р, е не могут входить в этот граф, так как их степень

(рис. 3.60,6) меньше 4. Удаляем вершины Ь, р, е из графа G' (рис. 3.60,6); по

лучаем граф, изображенный иа рнс. 3.60, в, который ни по вершинному ресурсу,

ни по реберному, нн по локальной топологии не может содержать граф Q(4, 1).

Следовательно, км»кс = 0 при р — 4.

Уменьшим плотность на 1 и определим максимальное значение к:

'10-3

Следовательно, заданный граф не может содержать квазиполный граф Q(3, 2).

Бше раз уменьшаем плотность на единицу и определяем максимальное значение

к при р = 2. Имеем

*(G0=]log2 ( i ^ + l) [ = l.

§3.10. Логарифмические оценки хроматического числа

247

Таким образом, заданный граф ие содержит даже квазиполного графа Q(2, 2).

Отсюда верхняя оценка хроматического числа h(G) графа G равиа 4. Она со

впала с нижней оценкой p(G) < h(G). Следовательно, хроматическое число

заданного графа также равно 4: ki = {Ь, d, р, g}, ki = {а, с, е}, кз = {ш, /} ,

kt = {А:} (рис. 3.60,г).

Таким образом, использование характеризации раскраски вершин графа по

зволило в данном случае определить его хроматическое число, ие находя мини

мальное покрытие пустых подграфов вершинами графа.

Для графа G, содержащего разложимый квазиполный граф,

хроматическое число h(G) согласно теореме 3.47 равно сумме хро

матических чисел квазиполных графов, которые являются слагае

мыми графа Q(q) С G максимальной квазиплотности. Поэтому

где max J2kij(Qij) определяется на основании (3.40), (3.41), (3.46).

Пример 3.20. Определим хроматическое число h(G) графа G = (V, U)

со следующими параметрами: \V\ = 90, \U\ — 556, p(G) = 6. Распределение

степеней вершин таково: 32 вершины имеют степень меньше 5; 16 вершин —

степень 5; 12 вершин — степень 7; 2 вершины — степень 8; 25 вершин —

степень 9; 2 вершины— степень 1 1 ; 1 — степень 12.

Рассмотрим все случаи разложения 6 иа слагаемые: 1) 6 = 6+0; 2) 6 = 2+4;

3) 6 = 2 + 2 + 2; 4) 6 = 3 + 3.

Случай 1 . Определим максимальный порядок fcm»x неразложимого квази

полного подграфа Q(6, кт*г) плотности 6; при этом число вершин берем 74, так

как вершины со степенью, меньшей 5, в этот подграф не входят. Согласно (3.40)

Установим, может ли заданный граф G содержать квазиполный граф Q(6, 4),

по реберным ресурсам и локальной топологии (по значениям степеней вершин).

Имеем

\U\ > 0, 5 • (7 • З4 + 6 • 24 • (6 - 3) + (6 - З)2 - 6 + 2) =

= 0, 5 • (567 + 288 + 5) = 430,

h(G) = ina xqiiQi) = т а x ^ g ;j(Q y ),

QijCQi, Qi = 52Qij>

(3.56)

< max 5 2 PH (Qij) + mf x 5 2 W 'i) >

j j

h(G)<p(G) + m zx52kt:(QtJ),

№ „(<3(6, 4))| = 3 • (24 - 1) + 6 = 51,

(Vv;(vi € Q(6, 4)))(a(«i) > 6 + 4 - 1 = 9).

248

Гп. 3. Теория графов и мографов

Число вершин со степенью 5(и,) > 9, равно 28; 28 < 51. Следовательно, не

разложимый квазиполный подграф Q(6, 4) не содержится в графе G. Уменьшая

порядок на 1, получаем

|^min(Q(6, 3))| = 3 • (23 - 1) + 6 = 27,

(V«/.(«/. € Q(6, 3)))(s(vj) > 8).

Таким образом, получеи положительный ответ. Следовательно, определена

верхняя оценка: h(G) < 9.

Случай 2. Квазиполный граф Q(qUiKс) максимальной квазиплотности

можно разложить иа два слагаемых:

Q(2, ка) + Q{4, кь)-,

при этом h(G) < 6 + max(fca + кь). Определим шах(ка + кь). Для этого опреде-

о,6 о,Ь

лаем

ка = ]log2 + i ) [ = 4, \VM„(Q(2, 4))| = 3 • (24 - 1) + 2 = 47.

Второе слагаемое содержит 27 вершин: 74 — 47 = 27. Тогда

кь = ] log2 + 0 [ = 3’ 1Км,,(д(4, 3))1 = 3 • (23 - 0 + 4 = 25,

(Vvi(vi е Qо(2, 4)))(а(и,) > ра + ка - 1 + |V^M..(Qi,(4, 3))| =

= 2 + 4 - 1 + 25 = 30),

€ Qb(4, 3)))(s(vi) >рь + кь - 1 + |К,нн(<3(2, 4))| =

= 4 + 3 - 1 + 47 = 53).

Вершин с такими степенями в графе G нет. Продолжая аналогичные вычи

сления, находим, что т а x(jfc0 + кь) = 2 + 2 = 4 не выполняется, т. е. в графе G

а,Ь

не может содержаться квазиполный граф Q(10), разложимый в виде суммы

Qb(2, 2) + <?ь(4, 2).

Действительно,

|^м..(0а(2, 2))| = 3 • (22 - 1) + 2 = И,

|К «««М 4, 2))| = 3 • (22 - 1) + 4 = 13,

(Vu. € Qa( 2, 2))(a(uj) > 2 + 2 — 1 + 13 = 16),

(Vui € Qb(4, 2)j(j(»i) > 4 + 2 - 1 + 11 = 16),

|^ ..(Q a (2, 2))| + \UH„(Q b(4, 2))| + \V„m(Qa(2, 2))| • |K...(Q*(4; 2))| =

= 0,5 • (7 • 32 + 6 • 22 • (2 - 3) + (2 - 3)2 - 2 + 2) +

+ 0,5 • (7 • 32 + 6 • 22 • (4 - 3) + (4 - 3)2 - 4 + 2) + 11 • 13 = 206.

В этом случае хроматическая оценка h(G) не изменяется. Остальные случаи

предлагаем рассмотреть читателю самостоятельно. Окончательно получаем 6 <

< h(G) < 9.

Используя оценки Геллера — Брукса, мы получили бы отрезок [2, 13]:

2 < h(G) < 13.

Согласно (3.42) запрещенными фигурами раскраски вершин

графа в а красок являются квазиполные графы квазиплотности

а + 1.

§ 3.10. Логарифмические оценки хроматического числа 249

Теорема 3.51 (М.В. Горбатова). Квазиполный граф Q(p, к),

к > 1 , не обладает свойством реберности.

Действительно, если порядок к квазиполного графа Q превы

шает 1, то найдется вершина va, входящая более чем в 2 пол

ных подграфа. Такой вершиной является, например, вершина

замыкающего слоя. Согласно теореме 3.37 такой граф не обладает

свойством реберности.

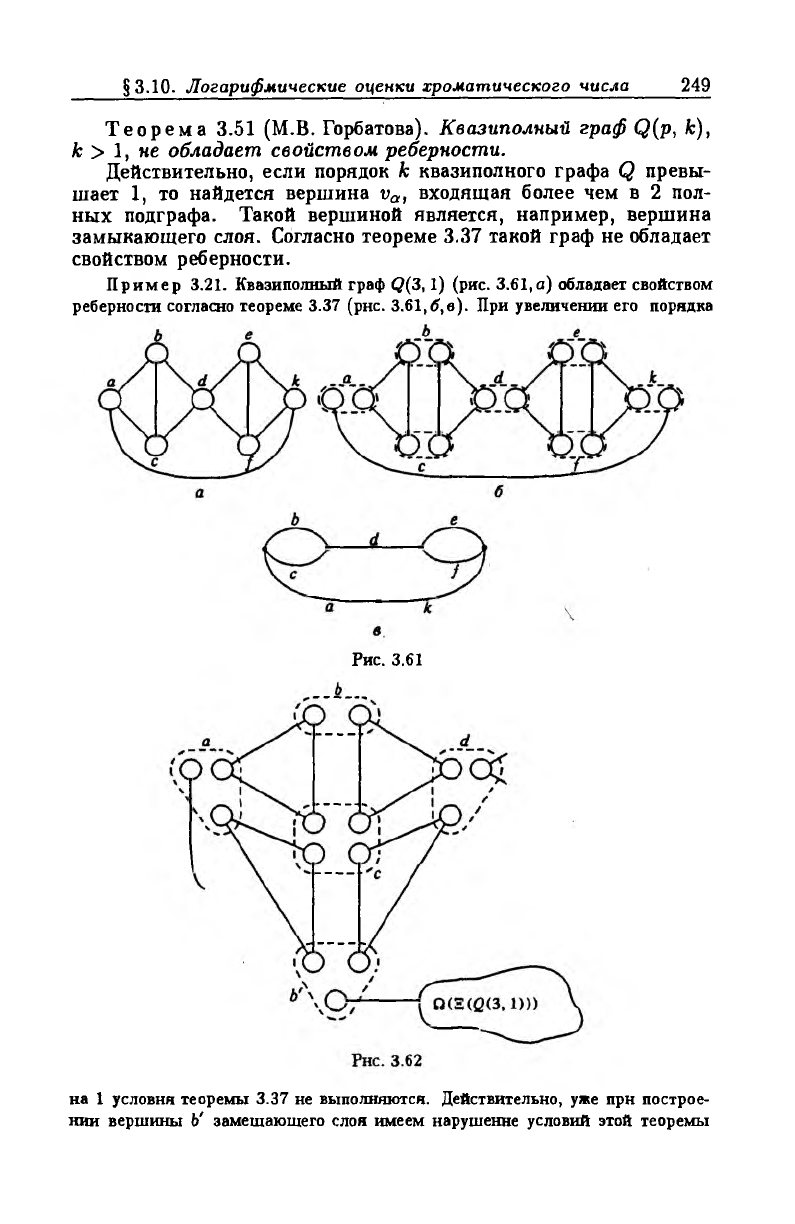
Пример 3.21. Квазиполный граф Q(3,1) (рис. 3.61,а) обладает свойством

реберности согласно теореме 3.37 (рнс. 3.61,б,в). При увеличении его порядка

Рис. 3.61

на 1 условия теоремы 3.37 не выполняются. Действительно, уже прн построе

нии вершины Ь' замещающего слоя имеем нарушение условий этой теоремы

250

Гл.З. Теория графов и мографов

(рис. 3.62). Вершина Ъ' является двойником вершины Ь: IV = Гь для вершин

основания — Q( 3, 1).

Если граф обладает свойством реберности, то его порядок не

превышает 1. При построении реберно производного графа G по

графу G ребра, инцидентные одной и той же вершине графа G, со

ответствуют вершинам полного подграфа графа G. Следовательно,

s < H { G ) < s + 1, (3.57)

где H(G) — хроматический класс графа G, s — степень графа G,

s = maxs(u;), и,- € G.

Для мультиграфа

s < H {G ) < s + p, (3.58)

где р — параллельность мулииграфа, т. е. максимальное число

параллельных ребер.

В соотношении (3.58) степень графа G и его параллельность

удовлетворяют следующим соотношениям (рис. 3.63):

s = 0(modp), s ф р, (3.59)

где запись s = 0 (modр) означает, что число s сравнимо по модулю

р с числом 0. Согласно (3.58) и (3.59) получаем оценку Шеннона

H (G )<

(3.60)

Рассматривая характеризацию раскраски графа, интересно

вспомнить проблему четырех красок. Эту проблему можно с пол

ным основанием назвать еще “болезнью четырех красок”, так

как она во многом похожа на заболевание.

“Она в высшей степени заразна. Иногда

она протекает сравнительно легко, но в не

которых случаях приобретает затяжной

или даже угрожающей характер. Никаких

прививок от нее не существует; правда,

люди с достаточно здоровым организмом

после короткой вспышки приобретают по

жизненный иммунитет... Тем не менее

именно попытки обосновать эту гипотезу

стимулировали получение ряда результа

тов по раскраске графов, которые в свою

очередь привели к исследованиям некото

рых других разделов теории графов”, —

так пишет ведущий графист, профессор

математики Мичиганского университета

Рис. 3.63 Фрэнк Харари [31].