Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§3.7. Раскраска вершин и ребер графа

211

Если наложить ограничения на декомпозицию исходного графа

G, а именно при разложении графа G на полные подграфы не до

пускать повторения ребер в полных подграфах, то реберно произ

водный граф G не будет содержать параллельных ребер, т. е. он

будет обыкновенным графом.

Теорема 3.38. Граф G обладает свойством реберности и

соответствующий ему реберно производный граф G является

обыкновенным графом тогда и только тогда, когда сущест

вует разбиение сигнатуры графа G ка полные подграфы, в ко

торые каждая вершина входит не более двух раз.

Пример 3.14. Определим, имеет ли граф G = (V, U) (рис. 3.38) реберно

производный граф. Граф G можно разложить иа 4 полных подграфа:

G = U Fi,

{а, Ь}, {а, е}, {Ь, е });

{а, с}, {а, d}, {с, d }};

{Ь, с], {Ь, fc}, {с, fc}};

{d, е}, {d, fc}, {е, k}}.

Ft = (Vi, Ut), Vi = {a, b, e}, Ui =

F2=(V2,U2), V3 = {a,c,d}, U2 =

F3 = (V3,U3), V, = {b,c,fc}, U3 =

F< = (V<,U<), Vt = {d, e, fc}, Ut =

Каждая вершина Vi £ V входит в полные подграфы Fi, i = 1, ..., 4, по два

раза (рис. 3.38, а). Условия теоремы 3.37 выполнены, реберио производный граф

G изображен на рис. 3.38, б.

При построении реберно производного графа G = (V , U) ка

ждой вершине и; € V со степенью s(v,) > 1 сопоставляют вы

деленный в графе G полный граф F{ С G. Ребра, инцидентные

вершине и,- € V, взаимно однозначно соответствуют вершинам

графа G, образующим этот полный подграф F,-. Вершина и,- € V

со степенью s(u,) = 1 коинцидентна ребру pj,

которому соответствует вершина Vj £ V, вхо

дящая в выделенные полные подграфы один

раз.

Используя свойства реберной раскраски

гиперкуба, предложим оптимальный алго

ритм вложения графа G в гиперкуб. Оче

видно, что хроматический класс Н(Нп) п-

мерного куба Нп равен его размерности п:

Я(Я„) = п. При этом соцветные ребра гиперкуба образуют его

разрез. Например, при п = 3 каждое множество соцветных ребер

а = {{0,4}, {1,5}, {2, 6},{3, 7}},

Ь = {{ 0, 2},{1, 3},{4, 6}, {5, 7}},

с= {{0, 1}, {2, 3}, {4, 5}, {6, 7}}

образует разрез (рис. 3.39). В то же время множество ребер {{1, 3),

{2, 3}, {5, 7}, {6, 7}} также является разрезом, хотя при этом ре

бра не являются соцветными: не образуют пустого реберного под-

Рис. 3.39

212

Гл. 3. Теория графов и мографов

графа. Отсюда нетрудно доказать теорему 3.39, введя понятие

паросочетательного разреза.

Разрез называется паросочетательным, если его ребра обра

зуют пустой реберный граф.

Теорема 3.39. Граф G вложим в гиперкуб тогда и только

тогда, когда множество пустых реберных подграфов включает

все паросочетательные разрезы этого графа.

Из этой теоремы получаем алгоритм вложения графа G в ги

перкуб.

1. Строя соответствующее дерево, выделяем реберно независи

мые подмножества (пустые реберные подграфы). Ребрам каждого

из этих подграфов можно сопоставить одну и ту же краску.

2. Из полученного в п. 1 списка выделяем подмножества, каж

дое из которых образует разрез графа G.

3. Используя выделенные в п. 2 подмножества, раскрашиваем

ребра заданного графа.

4. Проверяем, образует ли каждое множество соцветных ребер

разрез графа. Если нет, минимальным сужением сигнатуры или

расширением носителя эквивалентируем (заменяем эквивалентом

в смысле решаемо^ задачи) заданный граф G графом G, удовле

творяющим условиям теоремы 3.39. Если да, переходим к п. 5.

5. Производим фактическое вложение графа, полученного в п. 4,

в булево пространство. При этом краска ребра взаимно однозначно

соответствует разряду двоичного вектора, идентифицирующего вер

шину гиперкуба. При переходе через ребро {и,-, Vj}, окрашенное

в г-ю краску, двоичные коды вершин и,- и vj отличаются в г-м

разряде.

6. Конец.

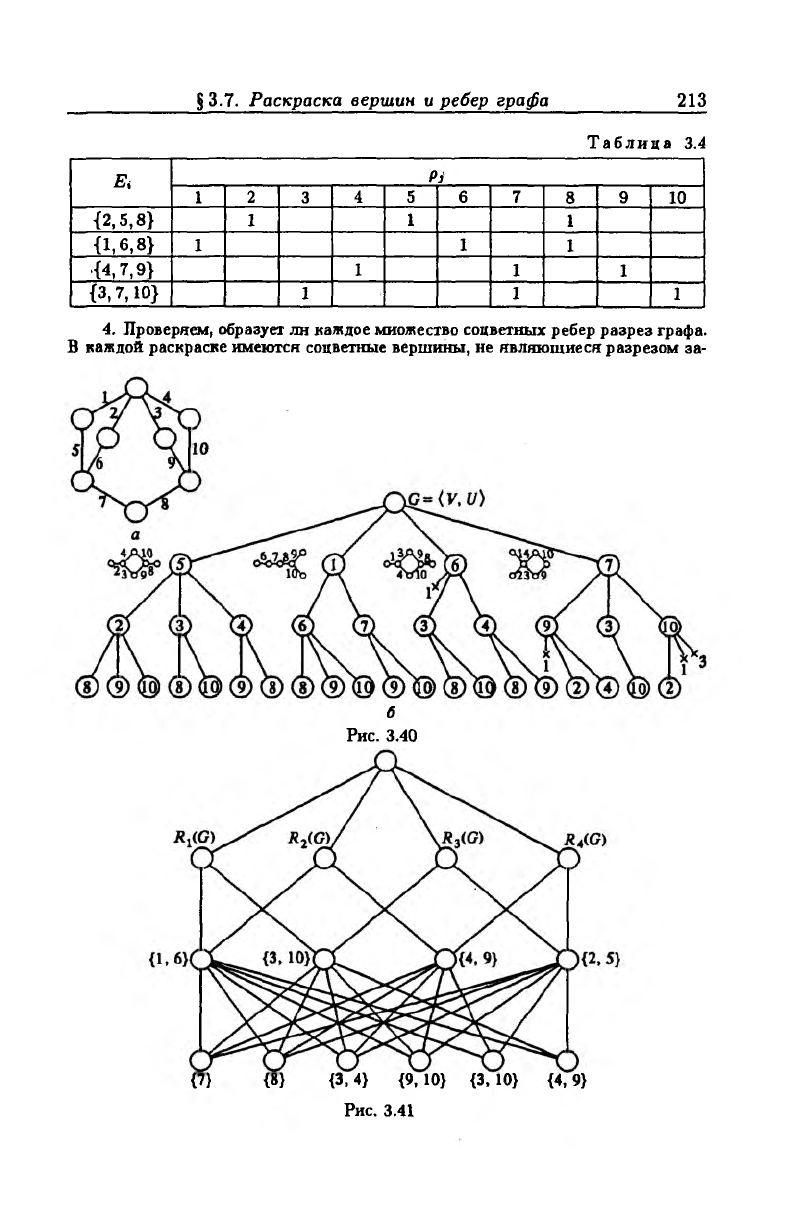
Пример 3.15. Вложим граф G (рис. 3.40,а) в булево пространство Н,

используя рассмотренный алгоритм.

1. Дерево, определяющее распределение пустых реберных подграфов, содер

жит 20 висячих верпгин, каждая из которых соответствует пустому реберному

подграфу (рис. 3.40,6).

2. Четыре пустых реберных подграфа образуют разрезы заданного графа:

Ei = {2, 5, 8}, Е* = {1, 6, 8}, Ез = {4, 7, 9}, Ел = {3, 7, 10}.

3. Раскрашиваем ребра заданного графа G с помощью покрытия столбцов

строками двоичной таблицы, в которой строке взаимно однозначно соответствует

пустой реберный граф, полученный в п. 2, столбцу — ребро, а на пересечении

i-й строки с j -м столбцом стоит 1, если i-й пустой реберный подграф содержит

j-e ребро, и 0 — в противном случае (табл. 3.4). Имеем четыре раскраски Ri(G)

графа G:

Ri(G) = {{2, 5, 8}, {1, 6}, {4, 7, 9}, {3, 10}},

R3(G) = {{2, 5, 8}, {1, 6}, {4, 9}, {3, 7, 10}},

Яз(G) = ({2, 5}, {1, 6, 8}, {4, 7, 9}, {3, 10}},

R<(G) = {{2, 5}, {1, 6, 8}, {4, 9}, {3, 7, 10}}.

§3.7. Раскраска вершин и ребер графа

213

Таблица 3.4

3 4

5 6 7

{2,5,8}

{1,6,8}

■{4,7,9}

{3, 7,10}

1 1

4. Проверяем, образует лн каждое множество соцветных ребер разрез графа.

В каждой раскраске имеются соцветные вершины, не являющиеся разрезом за-

Рис. 3.40

{7} {8} {3,4} {9,10} {3,10} {4,9}

Рис. 3.41

214

Гл. 3. Теория графов и мографов

данного графа: {1, 6}, {3, 10}, {4, 9}, {2, 5}. Для выполнения условий тео

ремы 3.39 необходимо удалить из графа G любой элемент множества {{7 }, {8},

{3, 4}, {9, 10}, {3, 10}, {4, 9 }}, выбрав соответствующую раскраску ребер гра

фа G (рис. 3.41).

Если предметная интерпретация задачи требует реализовать это эквивален-

тирование ие сужением сигнатуры, а расширением носителя, то соответствую

щие ребра заменяют цепью; при этом необходимо, чтобы ие нарушился прин

цип четности. Задача определения минимальных сужения сигнатуры или рас

ширения носителя графа G сводится к покрытию соответствующей двоичной

таблицы. В данном примере выбираем ребро 7 и, заменяя его цепью длины 3,

получаем гомеоморфный граф G, эквивалентируюший заданный граф G и обла

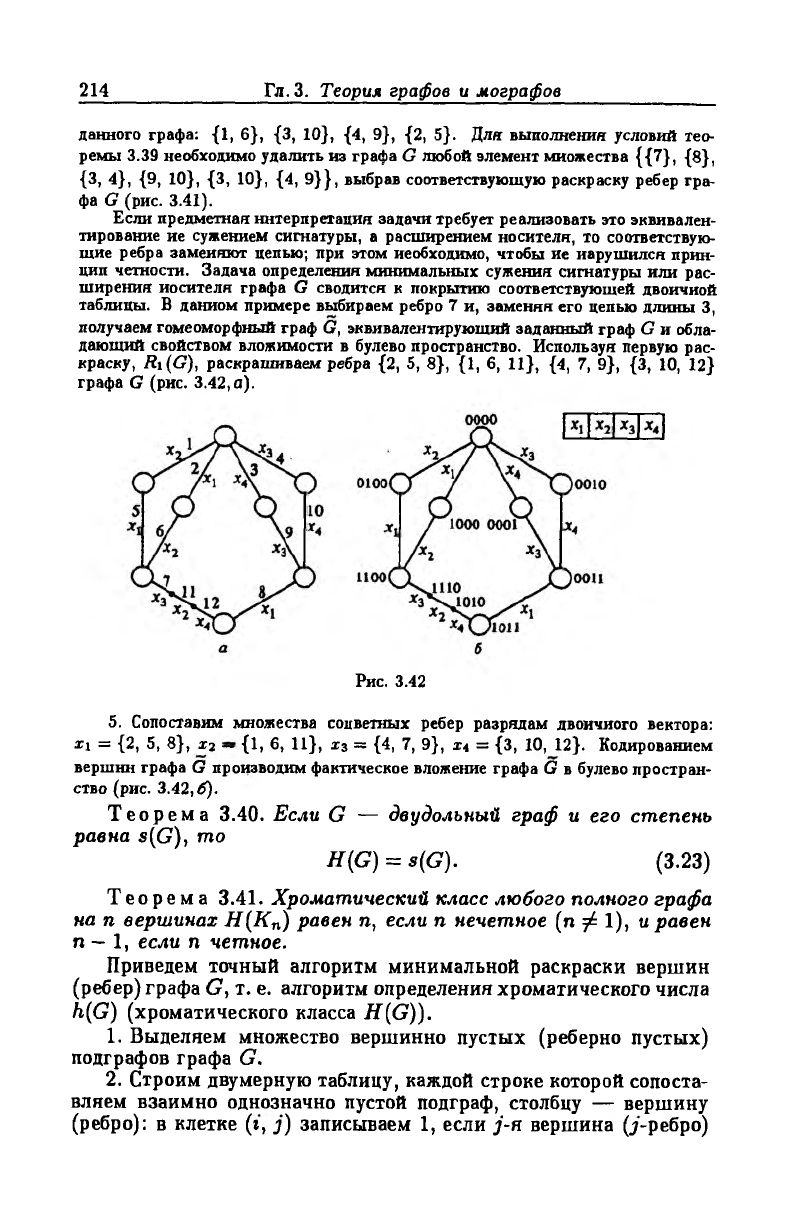
дающий свойством вложимости в булево пространство. Используя первую рас

краску, Ri(G), раскрашиваем ребра (2, 5, 8}, {1, 6, 11}, {4, 7, 9}, {3, 10, 12}

графа G (рис. 3.42,а).

Рис. 3.42

5. Сопоставим множества соцветных ребер разрядам двоичного вектора:

*1 = {2, 5, 8}, а — {1, 6, 11}, х3 = {4, 7, 9}, ц = {3, 10, 12}. Кодированием

вершин графа G производим фактическое вложение графа G в булево простран

ство (рис. 3.42, б).

Теорема 3.40. Если G — двудольный граф и его степень

равна s[G), то

H(G) = a(G). (3.23)

Теорема 3.41. Хроматический класс любого полного графа

на п вершинах Н(Кп) равен п, если п нечетное (п ф 1), и равен

п — 1, если п четное.

Приведем точный алгоритм минимальной раскраски вершин

(ребер) графа G, т. е. алгоритм определения хроматического числа

h(G) (хроматического класса H(G)).

1. Выделяем множество вершинно пустых (реберно пустых)

подграфов графа G.

2. Строим двумерную таблицу, каждой строке которой сопоста

вляем взаимно однозначно пустой подграф, столбцу — вершину

(ребро): в клетке (*, j) записываем 1, если j-n вершина (j-ребро)

§3.7. Раскраска вершин и ребер графа 215

содержится в t-м пустом подграфе; в противном случае клетку оста

вляем пустой.

3. Определяем покрытие столбцов строками. Каждое покрытие

порождает раскраску. Покрытие минимальной мощности опреде

ляет хроматическое число (хроматический класс) графа G.

В случае большого графа G = (V, U), когда мощность его носи

теля равна нескольким сотням и тысячам вершин, рассмотрим сле

дующий алгоритм [39], использующий частотные свойства графа.

1. Производя \U\ сравнений, определяем пару смежных вершин

va и vp графа G = (V-, U), для которого функционал

принимает максимальное значение. Равенство этого функционала

нулю означает, что ребро {иа> vp} не входит в треугольник, и чем

больше значение (3.24), тем в подграф большей плотности это ре

бро может входить.

2. Найденную пару вершин раскрашиваем, и им взаимно од

нозначно сопоставляем столбцы в двумерной таблице, строкам ко

торой взаимно однозначно сопоставляем вершины, смежные хотя

бы с одной раскрашенной вершиной; в клетке (г, j) ставим 1, если

i-я и j-n вершины смежны, и 0 в противном случае.

3. Выбираем строку с максимальным числом единиц.

4. Если для выделенной в п. 3 t-строки найдется j-й столбец, на

пересечении с которым находится 0, то соответствующую *-ю вер

шину раскрасим в j-ю краску и произведем склеивание соцветных

по j-ft краске вершин. В противном случае г'-ю вершину раскрасим

в новую краску, увеличивая количество столбцов в таблице на 1.

5. Если осталась хотя бы одна неокрашенная вершина, то пе

реходим к п. 3, в противном случае — к п. 6.

6. Конец.

Число красок при раскраске вершин графа G = (V, U) равно

количеству столбцов в итоговой таблице.

Пример 3.16. Раскрасим вершины графа G = (V, U) (рис. 3.43,а), ис

пользуя рассмотренный алгоритм.

(3.24)

Рис. 3.43

216

Гл. 3. Теория графов и мографов

I,J2. Максимальное значение функционала tp({va, v#}) согласно (3.24) равно

0,25 при рассмотрении вершин 1 и 4:

m&x<p({va, «э}) = 0,25, v0 = 1, vp = 4.

a, p

Получаем табл. 3.5.

3. Выбираем первую строку.

4. Раскрашиваем вершину 2 в новую краску, в результате получаем новую

табл. 3.6.

5. Неокрашенные вершины имеются; следовательно, переходим к п. 3.

3. Выбираем первую строку.

4. Вершина 3, соответствующая первой строке, соцветна вершине 1; раскра

шиваем вершину 3 и склеиваем ее с вершиной 1. Получаем табл. 3.7.

Таблица 3.5 Таблица 3-6 Таблица 3.7

vi е r«j

1 4

1 1

0 1

5 1 1

6 0

Vi 6 Г vj

1 4

3 0 1 1

5 1

1 0

0 1

Vi 6 Г vj

{1,3}

5 1

1 0

6 0

1 0

1 0 0

Выполняя этот алгоритм последовательно, получаем табл. 3.8-3.10.

Таблица 3.8

Таблица 3.9

Vi € Г vj

{1,3}

{2,5}

0 1 1

1 0 0

0 1

vi e г'vj

vi.

{1,3,6}

4 {2,5}

0 0

Таблица 3.10

vi € rvj

{1,3,6}

{4,7} {2,5}

8 0 1

Окончательно получена раскраска

исходного графа G — (V, U) в три

краски (рис. 3.43,6): а = {1, 3, 6, 8},

Ь = {4, 7}, с = {2, 5}. Плотность

графа G равиа 3. Следовательно, полученная раскраска является минимальной.

§ 3.8. Квазиполные модели, их структура и свойства

Будем рассматривать модели Ф со свойством симметричности

Ф = (М , Su S2, ..., S„>, SiC M \ i = 1,2, ...,n ,

т. e. каждое ребро модели представляет собой подмножество мно

жества М . В дальнейшем ребро будем называть словом, элемент

носителя М — буквой.

Подмоделью Ф' модели Ф называется модель Ф', полученная из

модели Ф вычеркиванием хотя бы одной буквы из слова, Ф' СС Ф.

Раскраской Д(Ф) модели Ф называется такое разбиение ее но

сителя, что ни одна из пар букв, входящих в слово, не принадле

жит подмножеству этого разбиения.

§ 3.8. Квазиполные модели, их структура и свойства

217

Обозначим множество красок минимальной мощности при рас

краске модели Ф через К{Ф):

ЯГ(Ф) = {<*/» = 1,2, h},

а раскраску — через Дтт(Ф)-

Квазиполной моделью ФQ(q) называется модель, в которой

при Дтт(Ф^) необходимо q красок, |К"(Ф^)| = q, а при Лтт(Ф').

Ф' СС Ф®, достаточно q' красок, q' < q. Число q(Ф^) при этом

называется квазиплотностью квазиполной модели Ф^.

Квазиплотностью q{Ф) модели Ф называется число

q( Ф) = тахд,(Ф?),

где Ф^ С Ф для любого i.

Плотностью р(Ф) модели Ф = (М, Si, S2, Sm) называ

ется число

р(Ф) = maxs,’,

где Si — степень словесного отношения S,- (t = 1, 2, . . т).

Порядком к(Ф) модели называется число

*(Ф) = д(Ф)-р(Ф).

Очевидно, что &(Ф) > 0.

Модель Ф квазиплотности q обозначим Ф(д). Модель Ф плотно

сти р и порядка к обозначим Ф(р, к). Краску Na, сопоставленную

буквам т а , mi2, ■ • •, mtn, обозначим Na(mn, т ,2, ..., m,n).

Частным случаем квазиполных моделей является квазиполный

граф.

Квазиполным графом Q(q) называется граф Q, для минималь

ной раскраски которого необходимо q красок, а при раскраске лю

бого собственного частичного графа Q , Q' С С Q, достаточно q'

красок, q' < q. Число красок q при этом называется квазиплот-

ностью квазиполного графа Q.

Квазиплотносхь q(G) графа G определяется выражением

q(G) = maxqi(Qi), Qi С G. (3.25)

Порядок k(Q) квазиполного графа Q(q) есть

k(Q)=q(Q)~p(Q). (3.26)

Порядок k(G) графа G есть

*(G) = 9(G )-p(G ). (3.27)

Условимся квазиполный граф Q плотности р и порядка к обо

значать Q(p, к), а граф с такими же характеристиками — G(p, к).

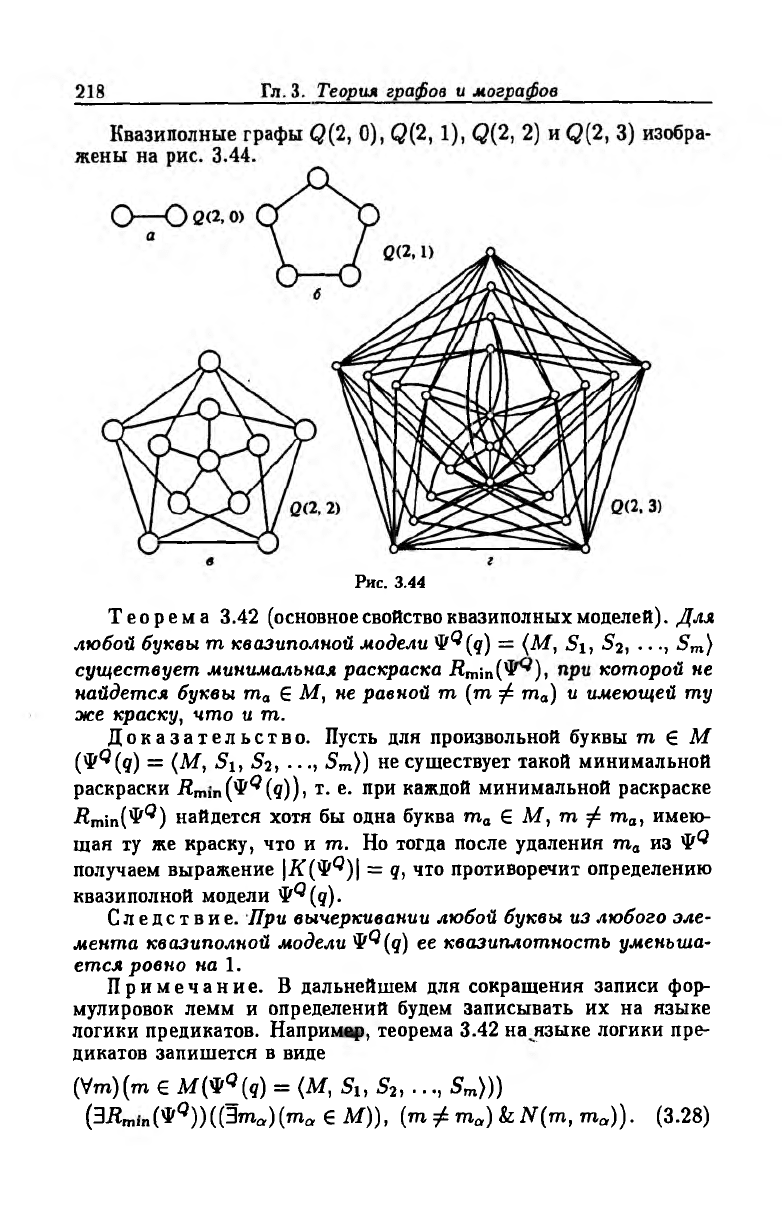
Рис. 3.44

Теорема 3.42 (основное свойство квазиполных моделей). Для

любой буквы т квазиполной модели Ф^(q) = (М , Si, S2, ..., Sm)

существует минимальная раскраска iimin(^ )> которой не

найдется буквы та Е М, не равной т (т ф та) и имеющей ту

же краску, что и т.

Доказательство. Пусть для произвольной буквы т £ М

(ФQ(q) = (М, Si, S2, ■ ■., Sm)) не существует такой минимальной

раскраски .йтт(Ф^(9))> т- е. при каждой минимальной раскраске

jRmin(Ф^) найдется хотя бы одна буква та € М, т ф та, имею

щая ту же краску, что и тп. Но тогда после удаления та из Ф^

получаем выражение |/^(Ф^)| = q, что противоречит определению

квазиполной модели Ф^(д).

Следствие. При вычеркивании любой буквы из любого эле

мента квазиполной модели ФQ(q) ее квазиплотность уменьша

ется ровно на 1.

Примечание. В дальнейшем для сокращения записи фор

мулировок лемм и определений будем записывать их на языке

логики предикатов. Например, теорема 3.42 на языке логики пре

дикатов запишется в виде

(Vm)(m € М(Ф^(д) = (М, Si, S2, ..., Sm)))

(ЗЛ1Пш(Ф<3))((З та)( т а € М)), ( т ф та) kN(m, та)). (3.28)

§3.8. Квазиполные модели, их структура и свойства 219

Для изучения структуры и свойств квазиполных моделей вве

дем алгебру Ak вида А* = (М, П, U, \), носителем М которой

является множество слов, сигнатурой — операции алгебры Кан

тора: П — пересечение, U — объединение, \ — разность. Каждое

слово ц при теоретико-графовом представлении модели Ф соответ

ствует полному подграфу плотности, равной |/х|.

Элементом носителя этой алгебры является модель Ф = (М, Si,

S2, • • -, Sn), определяющая множество подмножеств множества М,

которая является дистрибутивной решеткой; для нее справедливы

свойства идемпотентности

Да L) [Ха — Да, Да Да — Да

и поглощения

Да Г"1 (Да U Дь) = Да, Да U (Да П Дь) — Да.

Элементами модели Фа, Фа = Фь о Фс, где о обозначает одну

из операций U, П, \, являются полные подграфы, принадлежащие

графу Ста(Фа)) Ga(Фа) = Об(Фб) О Gc(^c).

Проиллюстрируем введенные операции над моделями:

Фь = {{а, *}, {х, р}, {р, о}, {тп, о}, {т, а}},

Фс = {{х, о,р}, {т , о, аг}},

Фа = Фь П Фс = {{г, р}, {р, о}, {т, о}},

Фа = ФЬ U Фс = {{г, о, р], {т, о, х}, {т, а, г}},

Фа = Фь \ Фс = {{а, х}, {т, а}}.

Из определения раскраски модели Ф очевидно, что число кра

сок определяется только топологией соответствующего ей мографа

GM(Ф), а порядок модели — как топологией, так и распределением

идентификаторов слов, взвешивающих вершины мографа GM(Ф),

а точнее — максимальной степенью словесного отношения. Ис

ходя из этого, при определении числа красок (в пределе — хрома

тического числа модели Ф) будем рассматривать мограф GM{^f)

без учета моделизации, т. е. без учета идентификаторов слов, взве

шивающих соответствующие вершины мографа GM(4f).

Вершина vj, v\ GM(Ф^), называется замещающей вершину

Vi, Vi € GM(^^), если их сечения равны друг другу:

г(ч)=г(«а.

Подграф G'-, G'- = (V/, Щ), G\ <£ GM(4!^)) называется заме

щающим подграф G,-, Gi — (VJ, Ui), G{ С GM(Ф^), если суще

ствует изоморфизм т/ между их носителями Vi A V(, при котором

г(ч) = г й , vit v' е v;, щ =

220

Гл.З. Теория графов и мографов

Факт замещения будем записывать в виде

G'i ='S(G.-).

Замещающим слоем Н(Ф^) квазиполной модели Ф^ = (М, Si,

5г, 5з, . . 5П) называется объединение U Н(Ф,) замещающих под-

графов Н(Ф,), при котором носители подграфов GM(^!i), СМ(Ф^) =

= (Mi, Щ, образуют разбиение носителя М модели Ф^:

У Mi = М, (V,0^,bi0, ц) (Mi, n Mib = 0 ).

При предельном рассмотрении квазиполная модель Ф^ и ее

замещающий слой Н(Ф^) могут совпадать: Ф^ = Н(Ф^).

Теорема 3.43.

(УДт!п(Ф<3(?)иН(Ф<3(д))(Е(Ф<3(д)) = (М, Slt Sa, ..., Sm)))),

(\/Ni£K(^(q))], (3meM)(N(m) = Ni).

(3.29)

Доказательство получаем, основываясь на определениях опера

ций над моделями квазиполной модели.

Содержательно замещающий слой Е(Ф^(д)) своими буквами

“замещает” все буквы модели Ф^(д), имеющие различные краски

при любой минимальной раскраске Rm “замещает” в том смы

сле, что каждая краска при любой Rm;п (Ф^(д) иЕ(Ф^(д))) соот

ветствует как букве та £ Ф^(д)* так и букве тр £ Е(Ф^(д)), т. е.

при любой минимальной раскраске Ф^(д) U Е(Ф^(д)) имеется q

различных пар букв (тпа, тр) таких, что

т а €Ф«(д), mpeZ(VQ(q)),

N(ma) = N(mp) = Щта, mp), i - 1,2,..., q.

В дальнейшем буквы, окрашенные одной и той же краской, при

минимальной раскраске будем называть соцветными.

Замыкающим замещающий слой Е(Ф^(д)) слоем П(5(Ф^ (д)))

называется совокупность вершин Vh, обладающая следующими

свойствами:

д г (,,) = и з ( ф « Ш ,

», € П(Н (*«(,))), (V0(»(»i)>S),

s(v,j — степень вершины у,-; V (~ (^(q ))) — носитель замещаю

щего слоя;

при минимальной раскраске вершин Vh необходимо g + 1

красок, а при удалении хотя бы одного ребра {уа, vp), va £

€ У’(Н(Ф<5(д))), vp £ Vh, достаточно g красок.