Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§4.1. Формальные грамматики

261

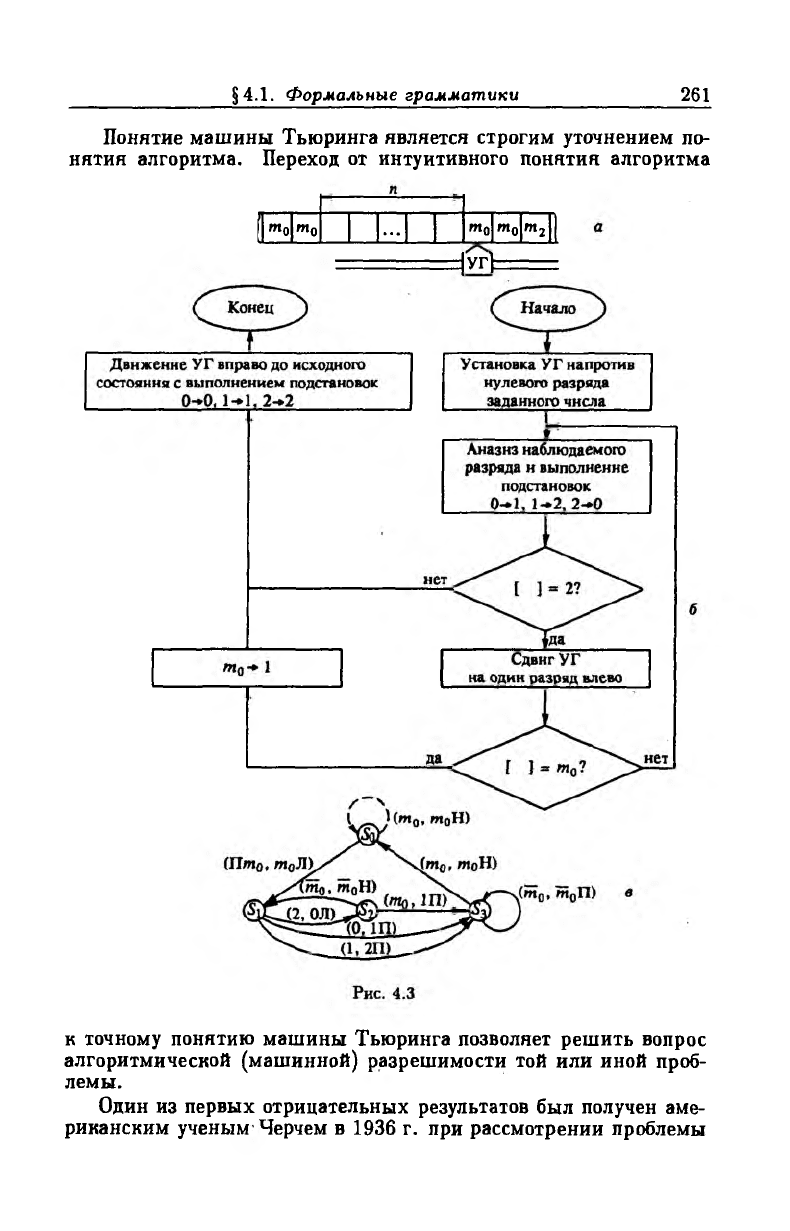
Понятие машины Тьюринга является строгим уточнением по

нятия алгоритма. Переход от интуитивного понятия алгоритма

[ т 0т 0

...

м0т 0

т2

yrj:

к точному понятию машины Тьюринга позволяет решить вопрос

алгоритмической (машинной) разрешимости той или иной проб

лемы.

Один из первых отрицательных результатов был получен аме

риканским ученым Черчем в 1936 г. при рассмотрении проблемы

262 Гл. 4. Теория формальных грамматик и автоматов

распознавания выводимости в математической логике: опреде

лить для любых заданных формул R и S в логическом исчислении,

существует дедуктивная цепочка, ведущая от R к S, или нет.

Бели формула А может быть преобразована в формулу В одно

кратным применением допустимой подстановки, и наоборот, то А

и В — смежные формулы. Последовательность А,-, * = 1,2,..., п,

формул, соседние из которых смежны, называется дедуктивной

цепочкой, ведущей от Ai к Л„. Под решением проблемы распо

знавания выводимости понимается алгоритм, дающий ответ на

вопрос о существовании дедуктивной цепочки (для любых R и S).

Проблема является алгоритмически неразрешимой, если не

существует алгоритма (соответствующей машины Тьюринга) для

ее решения. Отдельная машина Тьюринга может быть представ

лена как программа произвольного вида для ЦВМ с потенциально

бесконечной памятью.

Теорема 4.1 (Чёрч). Проблема распознавания выводимос

ти алгоритмически неразрешима.

Следуя Хомскому, введем ограничения на подстановки а —► (5,

прослеживая при этом соответствие полученной грамматики авто

матическому устройству.

Ограничение 1. Если а —► /? удовлетворяет выражению

(4.1), т. е. является правилом вывода, то

(3ai, а2, ..., ат, bi, Ь2, ..., Ьп(т < п)) ((а =

= aia2. ..am)k(/3 = М г- • • М ) • (4-2)

Язык, порожденный грамматикой, удовлетворяющей (4.2), ре

ализуется машиной Тьюринга.

Ограничение 2. Если а —>• /? — правило вывода, то

(З71, 72, a, 72, и> — цепочки, а — отдельный символ;

и не пусто)) ((а = 71072) & (/? = 7iw72)) • (4.3)

Грамматики, удовлетворяющие соотношению (4.3), называют

ся контекстными (контекстно связанными).

Контекстные грамматики реализуются устройствами типа ав

томата Майхилла.

Пусть (t, j, k, I, р) — одно из правил, определяющих работу

автомата: если блок управления находится в состоянии Sj, а счи

тывающая головка — напротив клетки, содержащей символ тп,-,

то блок управления может перейти в состояние £*, в то время как

лента продвигается в I клеток влево, а рассматриваемый символ

заменяется на тр. Устройство, работающее по такому принципу,

называется автоматом Майхилла.

Ограничение 3. Если а —► (3 — правило вывода, то a —

нетерминальная буква и

/3 Ф 0- (4.4)

§4.1. Формальные грамматики

263

Грамматика, удовлетворяющая (4.4), называется бескон

текстной (контекстно свободной).

Согласно (4.4) каждое правило грамматики утверждает, что

определенный нетерминальный символ может быть заменен це

почкой символов независимо от контекста.

Язык, порождаемый бесконтактной грамматикой, реализуется

автоматом Майхилла специального вида, в котором используется

магазинная память. Этот автомат, следуя Ньюэллу, Шоу и Сай

мону, будем называть магазинным автоматом.

Магазинный автомат представляет собой композицию управ

ляющего автомата и трех магазинов, каждый из которых пред

ставляет собой бесконечную в одну сторону ленту. На ленте запи

сано слово, первая буква которого записана в первой ячейке, вто

рая — во второй и т. д. При чтении воспринимается первая буква

слова, затем она стирается и оставшаяся часть слова сдвигается

к первой ячейке. При записи в магазин слова длины к первые к

ячеек освобождаются в результате записанного ранее сдвига слова

на к ячеек. Входной магазин связан с входными каналами упра

вляющего автомата, выходной — с выходными каналами, вну

тренний магазин связан как с входными, так и выходными кана

лами управляющего автомата. Множество внутренних состоя

ний управляющего автомата разбито на два подмножества, А и В.

Если управляющий автомат находится в состоянии, принадлежа

щем подмножеству А, то происходит считывание информации из

входного и внутреннего магазинов. Если автомат находится в со

стоянии Si € В, то происходит считывание только из внутреннего

магазина, при этом автомат переходит в следующее состояние и

записывает во внутренний и выходной магазины слова.

Правило бесконтекстной грамматики называется:

линейным, если оно имеет вид

А -+ хВу; (4.5)

праволинейным, если

А -* хВ\ (4.6)

леволинейным, если

А -* Вх. (4.7)

Правило вида А —ьх называется заключительным. В зависи

мости от ограничений, определяемых правилами (4.5)-(4.7), бес

контекстная грамматика может быть:

а) линейной, если каждое ее незаключительное правило ли

нейно (в частности, оно леволинейно или праволинейно);

б) односторонне линейной, если каждое ее незаключительное

правило леволинейно или каждое ее незаключительное правило

праволинейно;

в) металинейной, если все ее незаключительные правила либо

линейны, либо имеют вид S -* /3 и если, кроме того, в ней нет

правил вида А —► aS/З ни для каких А, а, /?, где а, /3 не пусты.

264 Гл. 4. Теория формальных грамматик и автоматов

Односторонняя линейная грамматика реализуется конечным

автоматом, и порождаемый ею язык называется конечноавто

матным.

Рассмотрим одностороннюю линейную грамматику, все пра

вила которой праволинейные (для определенности) либо заключи

тельные. Без потери общности можно предположить, что каждое

линейное правило имеет вид

А —► аВ, где В — неначальный сим

вол, и что каждое заключительное правило грамматики имеет вид

А а.

Пусть Ai, А2, ..., Ап — нетерминальные символы грамма

тики, причем Ai — начальный символ. Сопоставим грамматике

конечный автомат, каждое внутреннее состояние которого взаимно

однозначно соответствует нетерминальному символу грамматики,

а входной символ — терминальному символу грамматики. При

этом если А{ —¥ aAj — правило грамматики, то тройка (а, A,-, Aj)

определяет функционирование автомата и понимается как переход

от состояния Ai в состояние Aj при считывании входного сим

вола а.

Для определенности будем считать, что при переходе из со

стояния Si в состояние Sj в результате входного воздействия а

автомат вырабатывает на своем выходе символ Ь. Тогда автомат

можно определить как четверку (а, Ъ, Si, Sj).

Если фиксируется начальное состояние S0, то автомат реали

зует оператор Т: _

о — Т[а, Si, Sj),

который в дальнейшем будем называть автоматным.

Автоматный оператор Т переводит входную последователь

ность символов (а,) и выходную (b,j в зависимости от началь

ного состояния и реализуемой односторонней линейной грамма

тики. Автомат удобно представлять в виде функции Т на графе

G = {V, U), каждой вершине которого взаимно однозначно соот

ветствует состояние автомата, и если из состояния S,- в состояние

Sj автомат переходит в результате входного воздействия а, вы

рабатывая при этом выходной символ Ь, то соответствующие вер

шины Vi и Vj соединены дугой (ut, Vj), взвешенной парой (а, Ь).

Таким образом, областью определения этой функции Т является

граф G = (V, U), построенный рассмотренным выше способом, а

областью значений — входные, выходные символы и идентифи

каторы состояний автомата.

Рассмотрим, например, одностороннюю линейную грамматику

с алфавитом терминальных символов M j = {х, у, а, Ь}, с алфави

том нетерминальных символов Mpj = {Si, S2, S3} и следующими

правилами вывода:

Si —> ybS\, Si —¥ xaS2, S2 —> xaS2, S2 —> 1/0S3, S3 —> xbS\.

Эта грамматика реализуется конечным автоматом. Если авто

мат установить в начальное состояние Si и подать на вход после

§ 4.2. Основные этапы проектирования автоматов

265

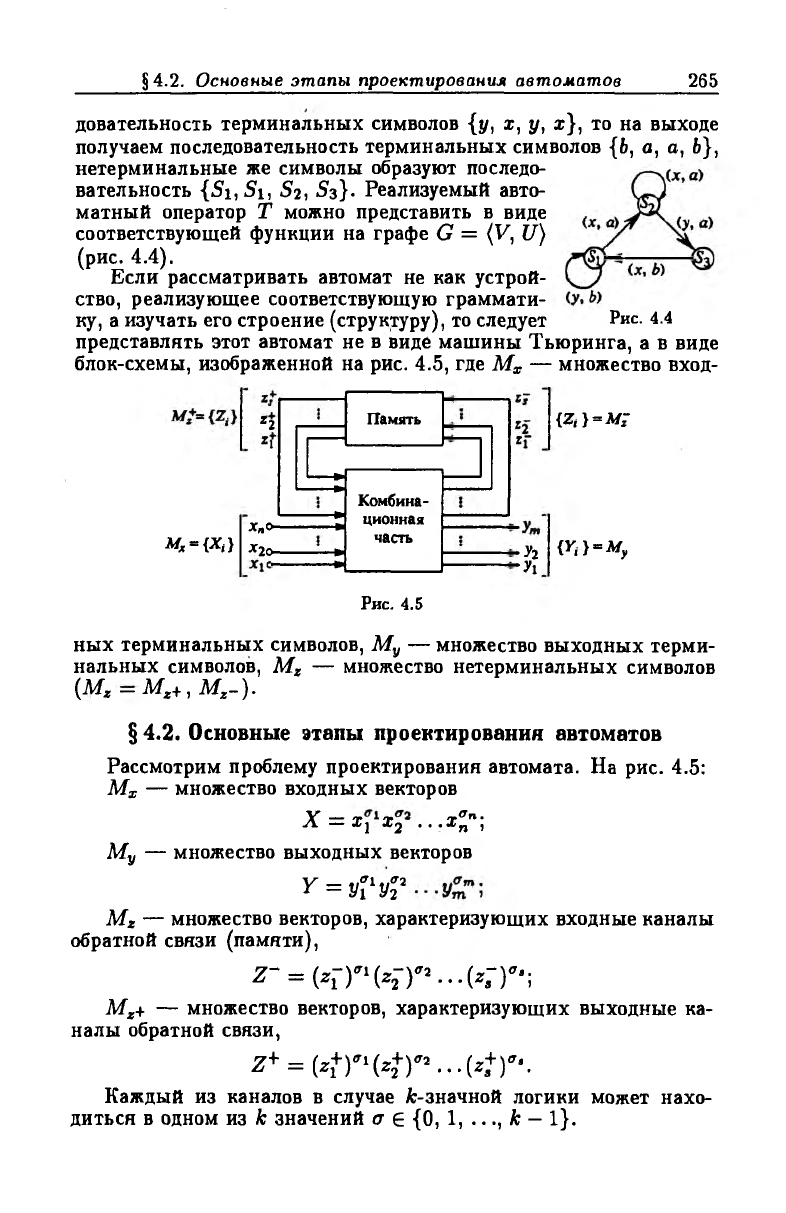
довательность терминальных символов {у, х, у, х}, то на выходе

получаем последовательность терминальных символов {Ь, а, а, Ь},

нетерминальные же символы образуют последо

вательность { S i , S i , S 2 , S 3 } . Реализуемый авто

матный оператор Т можно представить в виде

соответствующей функции на графе G = (V, U)

(рис. 4.4).

Если рассматривать автомат не как устрой

ство, реализующее соответствующую граммати

ку, а изучать его строение (структуру), то следует Рис. 4.4

представлять этот автомат не в виде машины Тьюринга, а в виде

блок-схемы, изображенной на рис. 4.5, где Мх — множество вход-

МЯ~{Х,}

Память

x„°-

X20-

Комбина-

ционная

часть

{Z,} = A/7

-Уг

-У1

{Y') = My

Рис. 4.5

ных терминальных символов, Му — множество выходных терми

нальных символов, Мг — множество нетерминальных символов

(Мг — Mz+, Mz~).

§ 4.2. Основные этапы проектирования автоматов

Рассмотрим проблему проектирования автомата. На рис. 4.5:

Мх — множество входных векторов

у _ ~<?п.

Л — Х1 х2 ...Хп ,

Му — множество выходных векторов

у = уГуГ

Mz — множество векторов, характеризующих входные каналы

обратной связи (памяти),

z - = ( z r r ( 2 2T ’ - - - ( * r r ;

Мг+ — множество векторов, характеризующих выходные ка

налы обратной связи,

z + = ( * f r ( 4 r - '- ( ^ r -

Каждый из каналов в случае fc-значной логики может нахо

диться в одном из к значений а £ {0, 1, ..., fc — 1}.

266

Гл. 4. Теория формальных грамматик и автоматов

Условимся обозначать переменную а, равную а € {0, 1, 2, ...

1}, как а17. Тогда правила вывода в случае автоматной

грамматики удобней определить как подстановку X Z + —> Z~Y, в

которой начальное значение вектора Z+ и последующие его зна

чения получаются приравниванием значению вектора Z~, вычи

сленному на предыдущем шаге, т. е.

Z+(f = 0) = Zo+, Z+(t + r) = Z -(t),

где г — некоторая постоянная времени автомата.

Векторы X Z + и Z~Y получаются приписыванием справа век

тора Z+ к X и У к Z- соответственно.

Состояния каналов обратной связи в дальнейшем будем назы

вать внутренними состояниями автомата, а постоянную вре

мени г — временем перехода из одного внутреннего состояния в

другое, причем в зависимости от назначения автомата и его реа

лизации т может быть постоянной для данного автомата или же

зависеть от изменения вектора X. В первом случае автомат назы

вают синхронным, во втором — асинхронным.

При заданном (Z+)о последовательность входных векторов X

(входная последовательность) однозначно определяет последо

вательность выходных векторов Y (выходную последователь

ность). Проиллюстрируем это на следующем примере.

Пусть имеется устройство с входным каналом г, каналом обратной связи z

и выходным каналом у, реализующее отображение XZ* -Л Z~Y, заданное в

виде таблицы (табл. 4.1),

Таблица 4.1 Таблица 4.2

Время X 2+

г~

0 1

т 0

1 1

2т 1 1 0 0

3 т 0

1 0

4т 0

1 0

5т 1 1 0 0

2+ z~

1 1

1 0 0 1

Определим выходную последовательность, если входная последовательность

имеет вид 101001 и начальное значение вектора Z + равно 0. В начальный мо

мент времени вектор XZ+, равный 10, определяет Z~Y = 01 (третья строка

таблицы). Через промежуток времени, равный г, условие XZ* = 00 определит

Z~Y = 11 (первая строка) и т. д. Запишем определение выходной последова

тельности в виде табл. 4.2. .

Z? s 0

Следовательно, 101001

---------

► 110100.

При Z f = 1 согласно заданному автоматному отображению входная после

довательность 101001 преобразуется в выходную последовательность 010100.

Таким образом, автоматное отображение X Z + —► Z~Y одно

значно определяет выходную последовательность (У;) по заданной

§4.2. Основные этапы проектирования автоматов 267

входной последовательности (Xi) и начальному внутреннему со

стоянию Zq : (Xi) — -—> (Yi).

Одной из основных характеристик автомата является объем

его памяти. Число внутренних состояний автомата называется

объемом памяти автомата.

Как известно, преобразование информации является резуль

татом выполнения некоторого алгоритма, при этом операционный

автомат реализует шаги алгоритма, а управляющий авто

мат — порядок выполнения шагов. Операционный и управля

ющий автоматы различаются не только своими назначениями, но

и объемами памяти. В операционном автомате происходит пре

образование информации, которая задана в виде некоторого мно

жества чисел, записанных в регистрах. Практически объем па

мяти операционного автомата бесконечен. Так, например, блок

регистров современной ЭВМ, входящий в операционной автомат и

состоящий из 22 16-разрядных двоичных регистров, имеет объем

памяти 2352 > Ю100 бит. Объем памяти управляющих автоматов

обычно составляет от нескольких десятков до нескольких десят

ков тысяч бит, т. е. является небольшим по сравнению с объемом

памяти операционных автоматов.

Рассмотрим взаимодействие операционного и управляющего

автоматов (рис. 4.6). На вход операционного автомата (канал 1)

поступает преобразуемая информация; с выхода операционного ав-

Операционный

Управляющий

автомат

4 5 61

Рис. 4.6

томата (канал 2) снимаются результаты преобразований; по ка

налу 3 поступают управляющие воздействия, соответствующие

реализуемому алгоритму; по каналу 4 на вход управляющего авто

мата поступают признаки, характеризующие преобразуемую ин

формацию; по каналу 5 — сигнал, определяющий выполняемое

преобразование и его начало; по каналу 6 — сигнал окончания

операции. Каналы 1 и S называются информационными, каналы

3-6 — управляющими. Рассмотрим, например, выполнение опера

ции сложения в арифметическом устройстве (АУ) ЭВМ. В данном

случае операционным автоматом является арифметическое устрой

ство, т. е. регистры, сумматор и связи между ними, а управляю

щим автоматом — устройство управления АУ.

При выполнении алгоритма сложения по каналу 1 из запоми

нающего устройства (ЗУ) машины в соответствующие регистры

268

Гл. 4. Теория формальных грамматик и автоматов

АУ записываются первое и второе слагаемые; по каналу 5 из цен

трального устройства управления (ЦУУ) машины поступает код

операции (сложение); по каналу 3 из управляющего устройства АУ

согласно алгоритму сложения посылаются управляющие сигналы:

сдвиг регистров, возбуждение соответствующих шин в сумматоре,

запись суммы в регистр результата и другие сигналы. По каналу

4 поступают признаки (например, содержание знаковых разрядов

в сумматоре, используемое для обнаружения нарушения нормали

зации), определяющие ход дальнейшего управления. По каналу

6 в ЦУУ передается сигнал окончания выполнения операции. По

каналу 2 в ЗУ посылается результат операции.

ЭВМ — сложный преобразователь информации, и ее целесо

образно рассматривать, следуя В.М. Гпушкову, как композицию

пар автоматов, каждая из которых состоит из операционного

и управляющего автоматов. При этом каждое устройство ЭВМ

(ввода, вывода, ЗУ, ЦУУ) представляется аналогично арифмети

ческому устройству в виде пары или нескольких пар таких авто

матов. Такое представление ЭВМ диктуется не только удобством

анализа и синтеза ЭВМ, но и является естественным развитием

структуры современных ЭВМ. В настоящее время как один из

методов увеличения производительности ЭВМ используется муль

типрограммный режим, что, в частности, уменьшает задержки,

вызываемые низкой скоростью внешних устройств и несоответ

ствием скоростей работы внешних и арифметических устройств.

Для реализации мультипрограммного режима ЭВМ необходима

некоторая “самостоятельность” отдельных устройств, т. е. воз

можность хранения, преобразования информации и управления

этим преобразованием внутри устройства; другими словами, необ

ходимо, чтобы каждое устройство представляло собой композицию

операционного и управляющего автоматов.

В настоящее время на основе нейротранспьютерных техноло

гий, создаются мощные вычислительные сети; примером таких

сетей являются Communication Machines (СМ-1, СМ-2), имею

щие кластерно-гиперкубовую архитектуру. Транспьютерная сеть

СМ-1 состоит из 65536 (216) транспьютеров, СМ-2 — из 4 194 304

(222) транспьютеров. В кластерах реализуются связи “каждый с

каждым”, каждый кластер соответствует вершине гиперкуба. Гео

метрически сеть СМ-1 представляет собой куб, длина ребра кото

рого равна 120 см, сеть СМ-2 — куб с ребром 480 см.

При проектировании ЭВМ можно выделить три основных эта

па: системный, логический и технический.

На этапе системного проектирования строится композиция

пар автоматов — операционных и управляющих (общая блок-схе-

ма ЭВМ); определяются необходимый объем памяти автоматов, их

взаимодействие на основе выбора системы команд, внешние и вну

тренние языки машины и т. д. Исходной информацией на си-

§4.2. Основные этапы проектирования автоматов

_______

269

схемном этапе является совокупность классов задач, для решения

которых предназначена проектируемая машина, и ее параметров

(быстродействия, стоимости, габаритных размеров и т. д.).

Рассматриваемые на этапе системного проектирования авто

маты имеют большой объем памяти, превышающий, как уже от

мечалось, Ю100 бит. Поэтому в настоящее время задачи систем

ного этапа решаются с помощью программного моделирования.

Процесс решения задачи системного этапа методом программ

ного моделирования обычно состоит из следующих шагов:

а) составление математической модели, отражающей важные

свойства моделируемого устройства или машины в целом;

б) построение моделирующего алгоритма, запись его на неко

тором языке, предназначенном для описания моделей ЭВМ;

в) реализация моделирующего алгоритма на ЭВМ;

г) анализ результатов и корректировка модели устройства или

машины.

Программное моделирование позволяет определить основные

характеристики проектируемой машины, “узкие места” ее струк

туры.

На этапе логического проектирования ЭВМ синтезируются

непосредственно логические (функциональные) схемы всех блоков

машины. Исходной информацией для этого этапа являются алго

ритмы функционирования блоков.

На этапе технического проектирования на основе логических

схем строятся принципиальные монтажные схемы и готовится

техническая документация для производства ЭВМ.

Логическое проектирование заключается в синтезе как опера

ционных, так и управляющих автоматов. В силу практически

бесконечного объема памяти операционных автоматов последние в

настоящее время синтезируются с помощью программного моде

лирования. И если для формализованного синтеза операционных

автоматов необходимо развитие теории бесконечных автоматов,

то для формализации синтеза управляющих автоматов возможно

применение теории конечных автоматов.

Согласно этой теории при проектировании управляющих авто

матов будем различать два основных этапа: построения автомат

ного оператора и структурного синтеза автомата.

I. Этап построения автоматного оператора. На

этом этапе производится построение системы выходных функций

Y = / ( X , Z+) и системы функций возбуждения Z~ = <р(Х, Z+).

Автоматное отображение, записанное в виде системы выход

ных функций и функций возбуждения, будем называть автомат

ным оператором.

Этап построения автоматного оператора в свою очередь состоит

из трех лодэтапов: алгоритмического, абстрактного и этапа коди

рования (размещения) внутренних состояний автомата.

270

Гл. 4. Теория формальных грамматик и автоматов

На этапе алгоритмического проектирования заданный опе

ратор А оформляется в виде алгоритма исходя из поставленных

требований (простоты выполнения операций, быстродействия,

максимального уменьшения аппаратурных затрат и др.). Поиск

оптимального алгоритма по заданному оператору А можно пред

ставить в виде дерева, каждая висячая вершина которого соответ

ствует определенному алгоритму, т. е. определенной композиции

операционного и управляющего автоматов. Для поиска оптималь

ного алгоритма необходим перебор всех висячих вершин, число

которых не известно и определяется степенью развития рассма

триваемых преобразований.

Пусть, например, необходимо синтезировать арифметическое

устройство, реализующее четырехместную операцию суммирова

ния. В зависимости от выбора алгоритма, реализующего это за

дание, получаем определенную блок-схему синтезируемого устрой

ства, характеризующуюся аппаратурными затратами и быстро

действием. В данном случае можно предложить, например, три

варианта алгоритма.

1-й вариант. Суммируем два первых числа, к полученной

сумме прибавляем третье число и к вновь полученной сумме при

бавляем последнее число. Этот вариант алгоритма характеризу

ется временем выполнения операции 7*1 и аппаратурными затра

тами в виде одного сумматора, четырех регистров, устройства

управления и необходимых каналов связи. Этому алгоритму со

ответствует блоксхема, изображенная на рис. 4.7, а.

2-й вариант. Суммируем одновременно первое число со вто

рым, третье — с четвертым, результаты записываем соответствен

но в первый и третий регистры, затем суммируем их на пер

вом сумматоре. Окончательный результат записываем в первом

регистре. Этот вариант выполнения задания А характеризуется

временем выполнения т2 и аппаратурными затратами, представ

ленными на блок-схеме этого варианта (рис. 4.7,6).

3-й вариант. Суммируем первые два числа на одном сумма

торе, вторые два — на втором сумматоре, полученные суммы —

на третьем сумматоре, результат записываем в первый регистр.

Этот вариант характеризуется временем выполнения операции гз

и аппаратурными затратами, приведенными на рис. 4.7, в.

Тот или иной вариант алгоритма, реализующего задание А,

выбирается исходя из конкретных ограничений на аппаратурные

затраты и на время выполнения заданных операций.

Каждая висячая вершина дерева поиска оценивается временем

выполнения данного преобразования и сложностью аппаратуры

(сложностью операционного и управляющего автоматов). Слож

ность операционного автомата оценивается непосредственным под

счетом аппаратурных затрат. Сложность управляющего автомата

можно оценить с помощью понятия производной от модели.