Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§3.10. Логарифмические оценки хроматического числа

_____

251

...1840 г. Идет заседание Королевского географического об

щества Англии. Профессор А. Мебиус обращается к слушателям

своей лекции с вопросом о количестве мастей в игральных картах:

“Почему четырр масти: крести, пики, черви, бубны? Почему не 5,

6 мастей?” После выдержки паузы А. Мёбиус формулирует задачу,

которая стала проблемой, не решенной в течение 123 лет: “Лю

бая карта на поверхности нулевого рода (плоскость, сфера) может

быть раскрашена в четыре цвета так, чтобы государства, имею

щие общую границу, были окрашены в разные цвета”. Этой проб

лемой увлеклись в 40-50-е годы прошлого века студенты-матема

тики Лондона, ее обсуждал А. де Морган. Первая волна интереса

спала. В 1878 г. о ней упоминал А. Кели, который опубликовал

в 1879 г. ее “доказательство”. В 1880 г. свои “доказательства”

дали Тейт и А. Кемпе. Но через 10 лет, в 1890 г., П. Хивуд их

опроверг.

Следующая волна интереса возникла уже в 50-х годах нашего

столетия в связи с бурным развитием вычислительной техники.

Габриэль А. Дирак [39] — один из ведущих европейских ученых-

графистов, изучающих раскраску графов, поставил вопрос о су

ществовании графа G, плотность которого равна 2 (p{G) = 2), а

хроматическое число принимает сколь угодно большое значение.

Положительный ответ на этот вопрос независимо друг от друга

дали А.А. Зыков [19], Дж. и Л. Келли [42], Татт [37] (эту статью

опубликовали Брукс, Смит, Стоун, Татт под псевдонимом мадам

Бланш Декарт), Я. Мыцельский [44].

Автор настоящего учебника “заразился” этой проблемой, бу

дучи студентом Московского энергетического института, в 1962 г.

получил ее доказательство и отослал в ведущий тогда журнал в

области естественных наук АН СССР — “Журнал эксперименталь

ной физики и вычислительной математики”.

В марте 1964 г. автор сделал доклад [5] о минимальной рас

краске графа на научно-технической конференции МЭИ и опубли

ковал его [4]. В этой статье было введено понятие квазиполного

графа, доказано, что распределение квазиполных графов опреде

ляет его хроматическое число, и доказаны основные свойства, из

которых следует:

— доказательство проблемы четырех красок;

— оценка хроматического класса H(G) графа G при раскраске

его ребер

S < H {G )< p + S,

где р — максимальное число параллельных ребер, S — степень

графа; для обыкновенного графа G S < H(G) < 5 + 1;

— взаимосвязь между 5 и р

5 = 0 (modp), 5 ф р\

252

Гл. 3. Теория графов и мографов

— оценка хроматического класса К. Шеннона

Проблему четырех красок стали изучать с разных сторон, экви-

валентируя ее формулировки. Наиболее полный обзор эквива

лентных формулировок (13 формулировок) привел Т. Саати [45].

Несмотря на многочисленные публикации по раскраске графов

(Г.А. Дирак, О. Оре [26,38], Ф. Харари [31], Г. Биркгоф [35],

А.А. Зыков [20], Я. Мыцельский [44], Дж. и А. Келли [42], В.А. Гор

батов [35], Г. Уитни [36], Г. Ходвигер [41] и др.), не все математи

ческие школы графистов “осознали” опубликованные результаты.

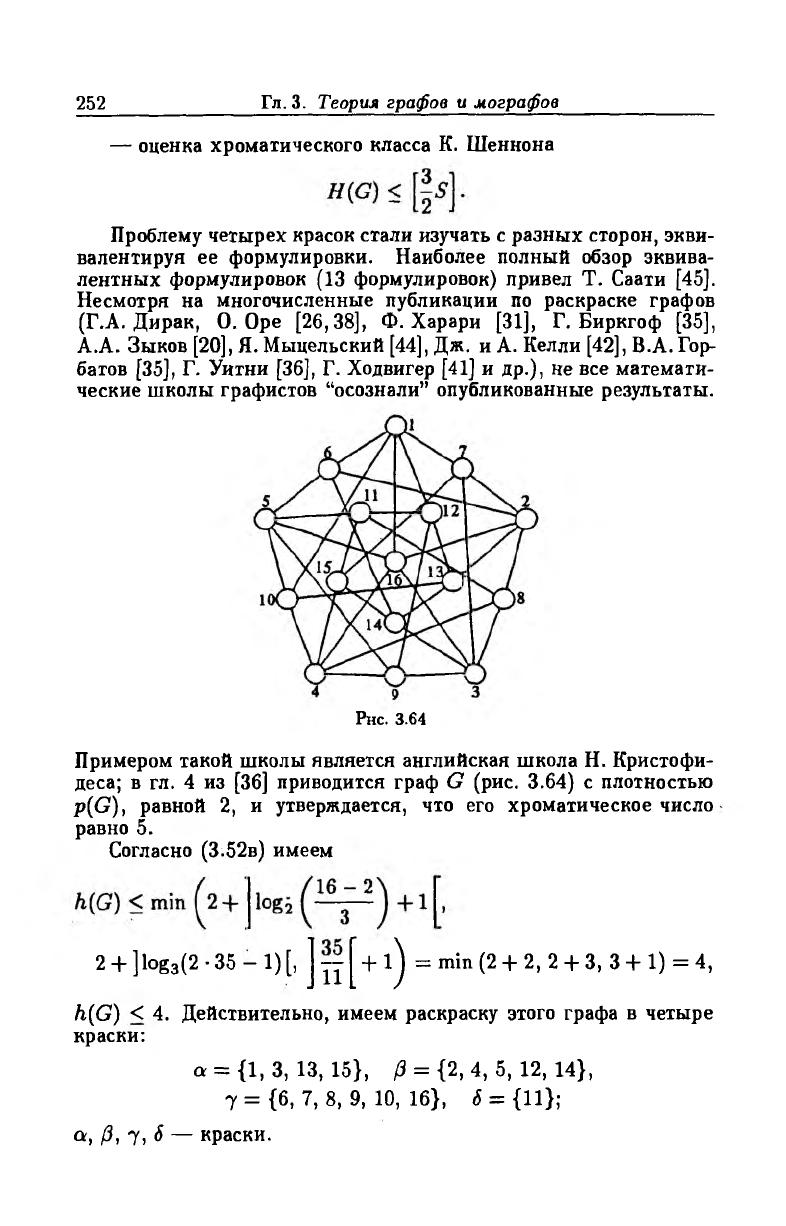
Примером такой школы является английская школа Н. Кристофи-

деса; в гл. 4 из [36] приводится граф G (рис. 3.64) с плотностью

p(G), равной 2, и утверждается, что его хроматическое число

равно 5.

Согласно (3.52в) имеем

h(G) < 4. Действительно, имеем раскраску этого графа в четыре

краски:

Рнс. 3.64

2 + ] log3(2 - 35 — 1)[, ] yx[ + i) =min (2 + 2, 2 + 3, 3 + 1) = 4,

о = {1,3, 13, 15}, /3 = {2, 4, 5, 12, 14},

7 = (6, 7, 8, 9, 10, 16}, 6 = {11};

а, /3, 7 , 5 — краски.

§3.10. Логарифмические оценки хроматического числа

253

Однажды в сентябре 1976 г. жители разных городов США

получили письма с марками, погашенными специальным штем

пелем, на котором было указано, что жители США К. Аппель и

У. Хайкин решили проблему четырех красок [33]. Решение осно

вывалось на результатах многочасовой работы мощного компью

тера.

Приведем доказательство проблемы четырех красок, получен

ное автором в 1964 г.

Теорема 3.52. Квазиполный граф Q(q) квазиплотности q

содержит подграф, гомеоморфный полному подграфу, плот

ность которого равна q.

Доказательство. Основание Q(q — 1) квазиплотного графа

Q{q) и их разность

Q(q) \ Q(q - i) = s(Q (g - 1)) и n(s(Q (g - 1)))

(q — 1)-вершинно связаны. Докажем это утверждение от против

ного. Пусть подграфы Q (q- 1) и Q (q)\Q {q- 1) [q - 2)-вершинно

связаны. Тогда существует множество (разрез 5), содержащее

(q — 2) вершины, после расщепления которых получаем две компо

ненты связности, Q(q - 1) и Q{q) \ Q(q - 1). В наихудшем случае

в разрезе 5 не найдется и двух соцветных вершин, т. е. вершины

разреза будут окрашены в д -2 краски. Тогда в основании Q(q — 1)

найдется вершина, окрашенная в (д - 1)-ю краску, так как его ква

зиплотность равна q — 1, а в разности Q{q) \ Q(q - 1) найдутся

две вершины, окрашенные в (q — 1)-ю и q-ю краски, так как для

любой вершины и,- G Q(q) найдется его раскраска R(Q(q)), при

которой вершины ее сечения Г(и*) окрашены в q — 1 различные

краски

К = {1, 2

......

q -

1},

(V«i € Q(q)){3R(Q(q))){\K(T(vi))\ = q - l).

Следовательно, как основание

Q(q

—

1), так и разность

Q{q) \Q{q — 1) содержат вершины, окрашенные в одну и ту же

(q - 1)-ю краску. Удаление одной из этих вершин не изменит хро

матического числа, что противоречит определению квазиполного

графа. Следовательно, эти вершины равны друг другу, и эта вер

шина, естественно, принадлежит основанию Q(q — 1). Но тогда

вершина основания Q(q), окрашенная в (q — 1)-ю краску, и вер

шина разности Q(q) \Q{q-1), окрашенная в g-ю краску, смежны,

что противоречит принятому допущению. Следовательно, основа

ние Q(g-l) квазиполного графа Q(q) и их разность Q{q)\Q{q — 1)

(q — 1)-вершинно связаны. Согласно теореме 3.7 любые две вер

шины Vi, Vj, Vi е Q(q - 1), Vj 6 Q(q) \ Q[q - 1), соединены no

крайней мере q — 1 вершинно непересекающимися цепями. Будем

254

Гл.З. Теория графов и мографов

рассматривать полный подграф F(p) плотности р как квазипол

ный граф Q(2, р — 2), в котором основания и замещающие слои

совпадают, а вершины замыкающих слоев конусируют соответ

ствующие основания. Учитывая свойство включаемости квазипол

ных графов (3.32) и выбрав ребро Q(2, 0), вершины замыкающих

слоев

n(E(Q(2, 0))),n(E(Q(2, l))),n(E(Q (2, 2)))

.......

n(S(Q(2, q -2)))

и соединяющие их цепи, получим подграф G, содержащийся в

Q(2, q - 2), G СС Q{2, q — 2) С Q(?)- На основании вышедо-

казанного утверждения о Q(q - 1)-связности полученный граф G

является гомеоморфным полному подграфу F(q) плотности q.

Теорема 3.53. Граф G(p, к), к > 1, р>2, невложим в плос

кость.

Действительно, граф G(p, к) содержит квазиполный подграф

Q(3, 2), который в свою очередь содержит подграф Gr(F(5)), го-

меоморфный полному подграфу плотности 5:

G(p, k ) jQ ( 3, 2) D Gr(F(5)).

Следовательно, согласно теореме 3.18 граф G невложим в плос

кость.

Теорема 3.54. Граф G(p, к), р>3, к > 0, невложим в плос

кость. f

Действительно, граф G(p, к) содержит подграф Q(4, 1), кото

рый содержит подграф Gr((F(5)), гомеоморфный полному под

графу плотности 5:

G (p ,k )D Q (4 ,l)D G r(F(5)).

Следовательно, согласно теореме 3.18 граф G невложим в плос

кость.

Теорема 3.55. Граф G(p, к), р = 2, к > 2, невложим в плос

кость.

Действительно,

G(P) к) Э Q(p, к) D Q{2, 3) Э Gr(F(5)).

Следовательно, согласно теореме 3.18 граф G невложим в плос

кость.

На основании теорем 3.53-3.55 получаем следующее доказа

тельство проблемы четырех красок.

Теорема 3.56. Хроматическое число планарного графа не

превышает 4.

Согласно теореме 3.18 планарный граф G не содержит под

граф Gr(F(5)), гомеоморфный полному подграфу плотности 5:

G Gr(F(5)). Следовательно, этот граф не содержит подграфы

§3.11. Задачи и упражнения

255

Q(2, 3), Q(3, 2) и Q(4, 1). Отсюда хроматическое число h(G) со

гласно теореме 3.48 не превышает 4.

А А Ф

$ А

fV \kl Ж

.А.

№

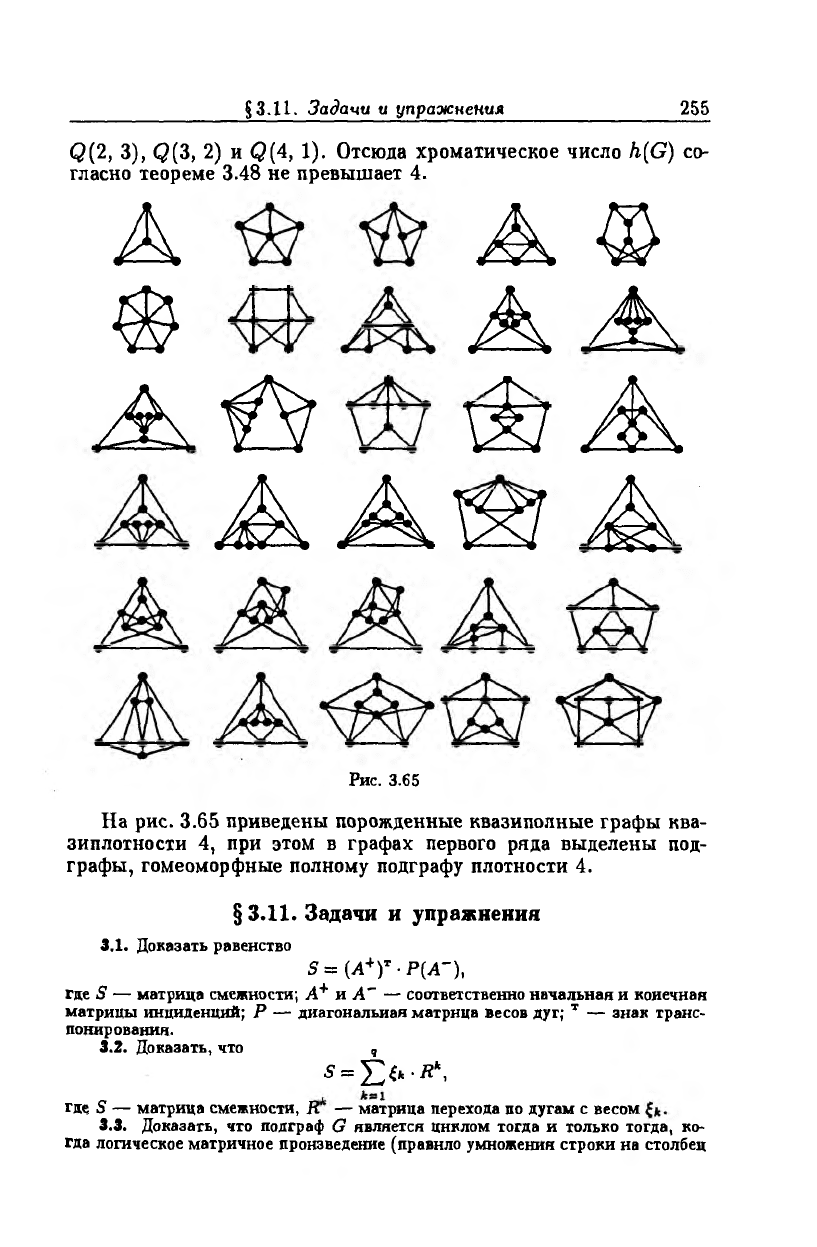
Рис. 3.65

На рис. 3.65 приведены порожденные квазиполные графы ква

зиплотности 4, при этом в графах первого ряда выделены под

графы, гомеомор фные полному подграфу плотности 4.

§ 3.11. Задачи и упражнения

3.1. Доказать равенство

5 = (Л+Г-Р(Л-),

где S — матрица смежности; А+ и А" — соответственно начальная и конечная

матрицы инциденций; Р — диагональная матрица весов дуг; т — знак транс

понирования.

3.2. Доказать, что ,

•* = ] [ > . Д \

где S — матрица смежности, R — матрица перехода во дугам с весом

3.3. Доказать, что подграф G является циклом тогда и только тогда, ко

гда логическое матричное произведение (правило умножения строки на столбец

256

Гл. 3. Теория графов и мографов

определено через обычное умножение и сложение по модулю 2) матрицы инцн-

денций и транспонированной дипломатической матрицы равно нулевой матрице.

3.4. Доказать, что простые пути длины I (I < q) графа, заданного матрицей

ч .

смежности S, определяются матрицей 5 , = 5 .

*=i

3.5. Пусть задан передатчик, который может передавать пять сигналов: а,

Ь, с, d, е. При приеме каждый из этих сигналов может быть истолкован двояко:

сигнал а как р нли q, сигнал Ь как q илн г, сигнал с как г нли а, сигнал d как з

нли t, сигнал е как р нли t. Какое наибольшее число сигналов можно принять,

не рискуя спутать нх друг с другом?

3.6. Доказать, что

a(Ga х Gb) > a{Ga) ■ a(Gb),

где ot(Gi) — число внутренней устойчивости графа Gt = Ga, Gb.

3.7. Определить число внешней устойчивости графа G, заданного матрицей

смежности

S =

3.8. Сколько ферзей достаточно расставить на шахматной доске так, чтобы

каждая клетка доски находилась под “ударом” хотя бы одного из них? Считать,

что клетка, занимаемая фигурой, также находится под ее “ударом".

3.9. Доказать, что число различных деревьев, которые можно построить на

п данных вершинах, равно п”' 2.

3.10. Найти связный подграф G' взвешенного графа G, заданного матри

цами, сумма весов ребер которого минимальна;

0 1

0 1 0

0 0 1 0

0 1

0 0

1 0

1 0 0 1 0 1 0 1

1 0 1 0

1 1 1 0

0 0 1 1

0 1 0

0 1

1 0

1 0 1

0 1

0 1 0

P(G).

2 0

0 0

4 0 0 0 0

0 3

0 0

0 1 0

0 0 0 0

0 9

0 0

0 0 0

0 2 0

0 0 0 0 0

0 0 0 0 0 0 0

3.11. Вершина графа, удаление которой вместе с инцидентными ей ребрами

делает граф несвязным, называется точкой сочленения. Блоком называется

связный нетривиальный граф, не имеющий точек сочленения. Может ли быть

блоком граф, цикломатическое число которого i/(G) = 2? Привести пример

блока, удаление одного ребра из которого приводит к появлению точки сочле

нения. Существует ли блок, в котором удаление любого его ребра приводит к

появлению точкн сочленения?

3.12. Привести примеры связных графов, для которых существуют разрезы,

число ребер которых равно числу хорд остовов.

3.13. Доказать, что удаление одного ребра, которое принадлежит какому-то

циклу связного графа, не делает этот граф несвязным.

3.14. Эйлеровым называется связный граф, в котором существует замкну

тая цепь, проходящая через каждое его ребро (все ребра цепи различны). Пока

зать, что граф, содержащий мост, не может быть эйлеровым.

§3.12. Комментарии

257

3.15. Граф называется гамильтоновым, если он содержит простой остов-

ный цикл. Привести примеры графов, которые одновременно н гамильтоновы,

и эйлеровы.

3.16. Определить число неизоморфных остовов двудольного графа К2, з-

3.17. Доказать, что если граф n-связен, то существует пара несмежных вер

шин, между которыми имеется п вершинно непересекаюшихся простых цепей.

Показать также, что это условие выполняется для любых двух несмежных вер

шин n-связного графа. Привести пример 3-связного графа.

3.18. Показать, что с точностью до изоморфизма имеется ровно 4 графа (один

из которых полный) без параллельных ребер и петель на трех вершинах, 11 —

на четырех вершинах. Определить количество графов иа пяти вершинах.

3.19. Реберным ядром графа G называется подграф, представляющий собой

объединение множества ребер у; таких, что ребра каждого множества попарно

несмежны н )у.| = ao(G). Привести примеры графов, не имеющих реберного

ядра. '

3.20. Найти необходимые условия, прн которых число ребер в графе равно

произведению ао/Зо.

3.21. Доказать или опровергнуть, что для любого связного графа (Зц < со.

3.22. Вычислить wi(Kmi„) и Ci(Km,„).

3.23. Доказать, что цикл нечетной длины невложим в n-мерный гиперкуб.

3.24. Показать, что диаметр n-куба d(G„) не может быть больше п.

3.25. Пусть граф G состоит из к вершинно непересекаюшихся простых цепей

между двумя вершинами о, b € G; длины всех цепей различны. Прн каком

условии этот граф кубируем?

3.26. Определить плотность графа, являющегося суммой ребра и цикла дли

ны 5.

3.27. Для графа, определенного в предыдущем упражнении, вычислить чи

сло внутренней устойчивости.

3.28. Для графа, являющегося произведением ребра н цикла длины 4, опре

делить число внешней устойчивости.

3.29. Найтн минимальную раскраску ребер графа Петерсена.

3.30. Обладает ли свойством реберности граф, являющийся суммой изоли

рованной вершины и цикла длины 5?

3.31. Вычислить хроматическое число графа Петерсена.

§ 3.12. Еомментарнн

Теория графов как раздел дискретной математики имеет многочисленные

Предметные интерпретации. Оиа успешно применяется в задачах управления

производством и при проектировании сетей ЭВМ, при разработке современных

электронных модулей и при проектировании физических систем с сосредоточен-

ными параметрами (акустических, механических, электрических), при решении

Проблем генетики и проблем автоматизации проектирования (САПР). Теория

графов является основой математического обеспеченйн современных систем об

работки информации. Эта теория находит применение в ядерных исследованиях

(диаграммная техника Фейгмана) и в финансовой области.

Более подробные сведения о теоретико-графовых моделях и их приложениях

Можно найти в [19, 26, 31, 44, 45].

9 В. А. Горбатов

В начале было слово.

Иоанн, 1.1

Глава 4

ТЕОРИЯ ФОРМАЛЬНЫХ ГРАММАТИК И АВТОМАТОВ

§ 4.1. Формальные грамматики

Рассмотрим систему подстановок, задаваемую алфавитом М =

= {тп,/ г = 1, . . р} и базисными подстановками

а,- -» fa, (4.1)

где а,-, Pi — формулы (слова), быть может, пустые в алфавите М.

Каждую подстановку а,- —>• /?,• будем понимать как правило вы

вода. Часто систему подстановок называют полусистемами Туэ

в честь норвежского математика Акселя Туэ. Используя эти по-

лусистемы, Н. Хомский (1955 г.) сформировал и развил аппарат

формальных грамматик.

Определим понятие формальной грамматики, которую в даль

нейшем будем называть просто грамматикой. Рассмотрим конеч

ный алфавит М = {mi, т2, ..., mn}, элементы которого будем

называть символами (буквами), а конечные последовательности

символов — словами.

Обозначим все множество слов, на длину которых не наложены

никакие ограничения, Яо. Будем говорить, что Я С Яо — язык в

алфавите М.

Пусть G — некоторая совокупность правил, с помощью ко

торых в М порождаются все слова, принадлежащие языку Я, и

только они. Совокупность правил G будем называть граммати

кой языка Я.

Два языка будем называть эквивалентными, если множества

слов, из которых они состоят, совпадают. Две грамматики, Gi и

G2, над называются эквивалентными, если языки, ими порож

даемые, эквивалентны.

Условимся говорить, что G — грамматика с конечным чис

лом состояний, если правила порождения слов из алфавита М =

= {mj, m2, ..., m„} задаются следующим образом. Существует ко

нечное множество состояний {5о, 5 i

.......

5Г} и каждому Sj (j = 1,

2,..., г) сопоставляется набор пар вида (пц, Sq), где *€{1,2,...

...,п}, q € {0,1

.......

г}. Состоянию So сопоставляются пары

вида (ого, ^л), где h £ {1, 2, ..., г}. Символ т о — специаль

ный знак пробела между словами. Конструирование слов проис

ходит следующим образом: из состояния So переходим в любое

§4.1. Формальные грамматики

259

состояние Sq. Из пар, сопоставленных выбранному Sg, берут лю

бую пару (mj, 5(). Этот выбор определяет следующее состояние

Si и первый символ слова тп,-. Далее про- м-{пц, т2, т 3}

цесс построения слова происходит анало

гично. Слово заканчивается при переходе

к заключительному состоянию, как прави

ло, Sq.

t Язык, порождаемый грамматикой и

конечным числом состояний, называется

языком с конечным числом состояний.

Структуру таких языков удобно изображать рИс. 4.1

в виде графа, вершины которого сопоста

влены состояниям Sj, а дуги — парам (тп,-, 5,). На рис. 4.1 при

веден пример такого графа. С помощью грамматики, задаваемой

этим графом, порождается язык, который состоит из следующего

множества слов:

{m imi, тхтпгтпзтх, mi m2m3m3mi тх m2 ( т 2) m^m^mi,

т 1т 2 ( т 2 ) т з т 1}.

Порождение цепочек символов можно рассматривать как ре

зультат работы некоторого гипотетического устройства (рис. 4.2).

Вдоль бесконечной (в обе или в одну сторону) ленты, разделен

ной на клетки, перемешается управляющая головка (УГ). Заданы

Рис. 4.2

внешний алфавит М = {m0, mi, т 2

.......

^п ), символы которого

называются буквами, внутренний алфавит S = {So, Si, ..., Sr},

символы которого называются

состояниями,

и алфавит переме

щений D = {Я, Л , Я }. Все клетки ленты заполнены символами

ИЗ М, по одному символу в каждой клетке. Символ то играет роль

Пустого символа (если в некоторой клетке стоит т 0, то в клетке

Ничего не записано). Предполагается, что вся бесконечная лента

всегда заполнена символами то, за исключением тех клеток, где

Записаны какие-либо другие символы из М.

Управляющая головка может находиться в тех или иных сос

тояниях, характеризуемых символами из S. Состояние So особое.

Если УГ находится в состоянии So, то машина не производит ни-

какой работы (выключена). Предполагается, что в конце работы

Машина всегда переходит в состояние So. В процессе работы ма

шины УГ может перемещаться в дискретные такты времени вдоль

Ленты. Перемещение происходит либо на одну клетку вправо (Я),

Либо на одну клетку влево (Л). Перемещение УГ в данный такт

работы может отсутствовать (Я).

I щ

щ т2

т2

—

УГ

—

260

Гл. 4. Теория формальных грамматик и автоматов

В каждый такт работы УГ совершает следующие действия:

1) считывает символ тп,-, находящийся в клетке ленты, которую

в этом такте видит УГ;

2) в соответствии со считанным символом т,- и своим состоя

нием Sj записывает символ тп* в эту клетку;

3) движется (не движется) вдоль ленты;

4) переходит в следующее состояние Sp.

Всю работу машины можно задать с помощью функциональной

таблицы Г, в клетках которой стоят тройки вида m*, Sp, di, где

d[ £ D — символ, определяющий перемещение. Таким образом,

функциональная таблица определяет отображение M xS в М х S х

xD. Содержательный смысл отображения (m,-, Sj) —► (m*, Sp, di)

состоит в том, что, находясь в состоянии Sj и считывая из клетки

символ тп,-, У Г записывает в данную клетку ленты символ тп*, пе

реходит в состояние Sp и производит движение, определяемое сим

волом di. Условимся, что функциональная таблица всегда устрое

на так, что имеет место отображение (m,-, So) —► (m,-, So, Н). Это

означает, что в выключенном состоянии машина не работает.

До начала функционирования машины (если это необходимо)

надо заполнить некоторые клетки ленты символами, отличными

от ш0, перевести УГ в состояние, отличное от So, и задать исход

ное положение УГ относительно ленты. После этого машина будет

функционировать в соответствии с таблицей Т. Функционирова

ние машины можно задать с помощью графа, вершины которого

взаимно однозначно соответствуют состояниям этого устройства,

дуги — переходам из одного состояния в другое, при этом каж

дая дуга (Si, Sp) взвешена парой (ггц, mkdi). Следуя Хомскому,

часто состояние называют нетерминальным (вспомогательным)

символом, символ тп,- С М — терминальным. Описанное гипоте

тическое устройство называется машиной Тьюринга.

Тезис Поста. Произвольная полусистема Туэ может

быть представлена как машина Тьюринга, и наоборот.

В гл. 1 было рассмотрено интуитивное определение понятия ал

горитма. Используя машину Тьюринга, уточним это понятие.

Тезис Тьюринга. Для любого алгоритма, понимаемого

в интуитивном смысле, можно построить машину Тьюринга,

функционирование которой эквивалентно этому алгоритму.

Синтезируем машину Тьюринга, реализующую прибавление 1

к целому n-разрядному числу, представленному в троичной сис

теме с алфавитом цифр {0,

1, 2} (рис. 4.3, а). Алгоритм реализа

ции этой операции представлен на рис. 4.3, б, где символ в квадрат

ных скобках обозначает содержимое наблюдаемого УГ разряда.

Введя нетерминальные символы Si, S2, S3, нетрудно определить

соответствующую машину Тьюринга (рис. 4.3,в),гдетпо = 0, 1, 2;

JI — левое движение на 1 разряд, П — правое движение на 1 раз

ряд, Н — движение УГ отсутствует.