Голдаев С.В., Ляликов Б.А. Основы математического моделирования в теплотехнике

Подождите немного. Документ загружается.

Министерство образования Российской Федерации

Томский политехнический университет

С.В. Голдаев, Б.А. Ляликов

Основы

математического моделирования

в теплотехнике

Учебное пособие

Томск 1999

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

УДК 536.24

Голдаев С.В., Ляликов Б.А. Основы математического моделирования в

теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

В учебном пособии рассмотрены все этапы математического моделиро-

вания от физической постановки задачи до анализа результатов расчетов,

описаны наиболее распространенные численные алгоритмы, проиллюстри-

ровано их использование на многочисленных примерах решения конкретных

задач из области теплотехники. Учебное пособие предназначено для студен-

тов энергетического направления. Пособие подготовлено на кафедре теоре-

тической и промышленной теплотехники ТПУ.

Печатает

ся по постановлению Редакционно-издательского Совета Том-

ского политехнического университета

Рецензенты:

В.А. Бураков – Ведущий научный сотрудник НИИ прикладной математики

и механики, д-р физ.-мат. наук;

Э.Р. Шрагер – Зав. каф. математической физики ТГУ, профессор,

д-р физ.-мат. наук.

й политехнический университет 1999

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Список условных обозначений

q -

плотность теплового потока, Вт/м

;

- интенсивность внутреннего тепловыделения, Вт/м

;

T -

абсолютная температура, К;

температура,

С;

время, с;

удельная массовая теплоемкость, Дж/(кг⋅ К);

плотность, кг/м

;

x,y

координаты, м;

толщина, м;

диаметр, м;

коэффициент теплопроводности, Вт/(м⋅К);

коэффициент температуропроводности, м

/с;

коэффициент теплоотдачи, Вт/(м

⋅К);

безразмерная температура;

безразмерные координаты;

число Фурье;

число Био.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Предисловие

При расчетах различных типов энергетических и технологических сис-

тем, на стадии так называемого поискового конструирования с выбором наи-

более оптимального варианта, требуется всесторонняя оценка теплообмен-

ных процессов, знание формирующихся в агрегатах температурных полей,

определения всех необходимых энергетических характеристик с учетом экс-

плуатационных нагрузок [1-10].

Математическое моделирование как метод исследования в настоящее

время получил широкое распространение [5

], [8], [11-16]. Математическая

модель, в отличие от реально поставленного эксперимента, имеет следующие

преимущества: 1) экономит материальные ресурсы, требуемые для постанов-

ки и проведения физического эксперимента; 2) предоставляет возможность

апробации системы в экстремальных условиях и даже за их пределами; 3)

оценка работоспособности систем с длительными технологическими цикла-

ми (недели, месяцы, годы) происходит в существ

енно более сжатые сроки

[12].

Математическое моделирование может проводиться и при оптимизации

технологического режима, при создании и внедрении в производство различ-

ных схем его автоматизированного управления [5], [7], [9], [10].

Анализ процессов теплоэнергетических систем показывает, что они могут

рассматриваться как совокупность элементарных процессов, каждый из ко-

торых вносит определенный вклад в скорость суммарного процесса [1-6

[14].

Многие элементарные задачи хорошо изучены, для них уже разработаны

методы численного решения [19-24], и нередко имеются соответствующие

программы, реализующие их на ЭВМ [20], [25], [26]. Однако формальное от-

ношение к алгоритмам, без вникания в их суть, может обернуться неудачей.

Например, попытка решения трансцендентного уравнения методом итераций,

когда оно не удовлетворяет условию сходимости этого процесса, не даст тре-

буемого результ

ата, численное интегрирование по явной схеме обыкновен-

ного дифференциального уравнения с большим шагом, вследствие неустой-

чивости этого алгоритма, приведет к физически неверным значениям и т.п.

По мнению авторов учебника [21], наибольший эффект в усвоении мате-

матических методов и приобретении навыков их применения достигается,

если изучение соответствующих разделов математики сопровождается реше-

нием прикладных задач, относящихся к области специализации будущего

инженера.

С этой целью в данном учебном пособии рассмотрены этапы математиче-

ского моделирования, описаны наиболее распространенн

ые численные алго-

ритмы, проиллюстрировано их использование на примерах решения ряда за-

дач из области теплотехники.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

1. ОБЩИЕ ПРИНЦИПЫ РАЗРАБОТКИ МАТЕМАТИЧЕСКИХ

МОДЕЛЕЙ ОБЪЕКТОВ ТЕПЛОТЕХНИКИ

При разработке математической модели сложного технологического про-

цесса по производству и передаче теплоты, выпуску продукта и т.п. выделя-

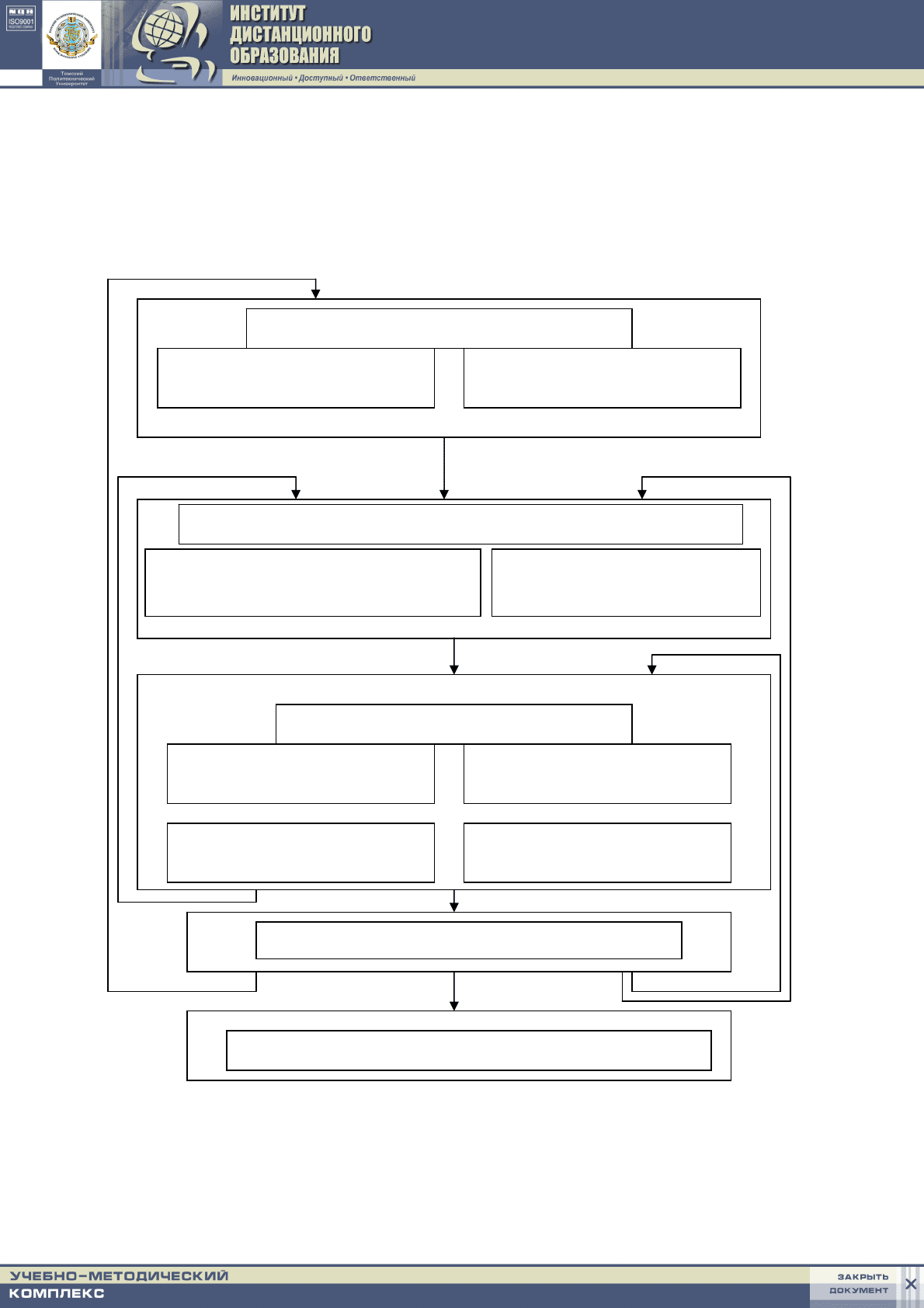
ют следующие стадии [12],[13], [21], [23], [24] (рис.1.1).

Постановка задачи моделирования

Формулировка задачи, вы-

бо

па

амет

ов п

есса

Определение цели и кри-

те

иев

Составление математического описания

Детерминированное описание:

выбор фундаментальных законов

Статистическое описание:

выбор зависимости

Использование математической модели

Установление адекватности модели

Программирование

Выбор численного мето-

Составление алгоритма

ешения

Выбор языка программи-

ования

Отладка программы

Рис.1.1. Этапы разработки математической модели

Рассмот

им особенности каждого из пе

ечисленных этапов.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

1.1. Физическая постановка задачи

На этом этапе необходимо не только формально представить задание, но

и сформулировать его, исходя из общей стратегии моделирования, степени

теоретической проработки процесса с учетом взаимосвязей с другими эле-

ментами.

Например, при построении физической модели работы контактных теп-

лообменников на стадии задания исходных данных формулируется ее цель,

определяются конструктивные, режимные пар

аметры аппаратов и уровень

рассмотрения процессов в них, уточняется критерий эффективности техноло-

гической схемы [18].

Если необходимо рассчитать температурное поле в металлической дета-

ли, то необходимо обосновать допущения о постоянстве теплофизических

свойств этого материала, одномерности процесса и т.п. Когда анализируется

многослойная система теплоизоляции на трубопроводе, то требуется сфор-

мулировать условие взаимодействия в зоне их контакта и правильно учесть

ее геометрию [28-31].

Ведущая роль при формулировке фи

зической модели объекта должна

принадлежать технологу (конструктору), т.к. только он может указать тре-

буемое множество переменных технологических параметров, определяющих

заданное качество объекта, а также сформулировать обязательные ограниче-

ния, связанные с реализацией в производстве поставленной задачи [5

], [12].

Участие математика на этой стадии необходимо, во-первых, для установле-

ния структурных связей между переменными и ограничениями, заданными

технологом; во-вторых, для внесения при недостатке исходных данных мето-

дических рекомендаций по совместной доработке построения модели.

На начальной стадии формулирования модели обеспечивается объем ра-

бот, аналогичный предпроектным оценкам при традиционном п

роектирова-

нии, включающим так называемые компоновочные решения.

1.2. Математическая постановка задачи

Математическое описание является отражением физической сущности

процесса со свойственными ему особенностями и ограничениями, которые

учитываются как при формулировании задачи, так и при составлении описа-

ния и выборе численного метода.

Наиболее распространенными подходами математических описаний яв-

ляются детерминированный и стохастический.

Детерминированная модель строится на основе фундаментальных и тео-

ретических законов и закономерностей. Он

а составляется, исходя из законов

термодинамики, законов сохранения массы, энергии, химической кинетики, и

учитывает такие явления, как диффузию, тепло – и массопередачу, гидроди-

намику [3], [4], [11], [13-18].

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Фундаментальные закономерности позволяют моделировать технологи-

ческий процесс с позиции идеализации происходящих явлений. Так, решение

многих задач математического моделирования элементов оборудования и

систем вентиляции основывается на уравнениях аэродинамики: неразрывно-

сти или сплошности потока, энергии, количества и моментов движения [26].

При расчете потерь давления в воздуховодах (каналах) и арматуре использу-

ются основные положения теории пограничного слоя, обусловленного сила-

ми вязкости, в пределах которого значение скорости меняется от нуля до

скорости невозмущенного (потенциального) потока. Толщина и характер по-

граничного слоя определяют процессы переноса колич

ества движения, энер-

гии и массы между потоком жидкости в целом и омываемой им поверхности.

При математическом моделировании течения воздуха в сетях вентиляции

и кондиционирова

ния рабочая среда считается несжимаемой, и это допуще-

ние не вызывает больших ошибок. Конечной целью исследования процессов

турбулентного движения воздуха в каналах является получение расчетных

зависимостей для вычисления аэродинамических сопротивлений сетей

транспортирования воздуха. По полному сопротивлению сети выбирается

давление, развиваемое вентилятором, и его характеристики.

Как известно, потенциальное течение происходит без в

ращения частиц

жидкости (газа). Существующие реальные течения лишь в определенной ме-

ре могут быть отнесены к потенциальным. Между тем в ряде случаев поня-

тие потенциального потока используется при изучении свободных потоков и

струйных течений; при обтекании потоком газа твердых тел, расчете полей

скоростей и давлений вокруг тела; при определении сил, действующих на об-

текаемое тело. Струйные течения возн

икают при подаче в помещения возду-

ха, обработанного в системах вентиляции и кондиционирования; сжигании

жидкого и пылевидного топлива в факельных печах; организации воздушных

завес для предотвращения прорыва холодного воздуха в здания и т.д.

Современные промышленные, административные и другие помещения

насыщены различным оборудованием, влияющим на развитие струй, кото-

рые в таких услови

ях называются стесненными. Изменение во времени рас-

хода приточного воздуха при истечении приводит к образованию пульсаци-

онных или импульсных струй. Удаление воздуха из вентилируемых и конди-

ционируемых объектов производят с помощью вытяжных устройств, при

этом у входных отверстий формируется воздушный поток, называемый вса-

сываю

щим факелом.

При исследовании сложных систем используются два взаимосвязанных

направления: 1) изучение процессов в элементах установок; 2) изучение ус-

тановок как систем взаимосвязанных элементов [17]. Работы по первому на-

правлению применительно к объектам теплоэнергетики связаны с анализом

теплообмена, гидродинамики, накипеобразования, сепарации паров и др. Во

многих случаях получена информация об элементах установок, необходимая

для выполнения со

ответствующих расчетов. Изучение же упомянутых объ-

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

ектов как сложных систем имеет принципиальное значение, т.к. процессы в

их элементах взаимосвязаны, и качественное математическое моделирование

возможно только при использовании вычислительной техники. Для реальных

процессов переход от идеальности обычно осуществляется с помощью эмпи-

рических и полуэмпирических зависимостей, полученных на реальных аппа-

ратах.

По целевому назначению математические модели разделяют на три клас-

са: модели для оптимального проектирования процессов и си

стем; модели

для исследования и оптимизации действующих процессов; модели для обес-

печения автоматизированного управления технологическим процессом [13].

Математическая модель сложного технологического процесса содержит в

качестве элементов модели отдельных узлов и агрегатов. В общей постанов-

ке задачи моделирования определяются требования к каждой из таких моде-

лей.

Например, выпарные установки состоя

т из следующих основных элемен-

тов: поверхностных выпарных аппаратов, конденсаторов смешения, самоис-

парителей конденсата и раствора, парожидкостных теплообменников и др.

Каждый из этих элементов характеризуется взаимодействием различных

процессов. Так, в выпарных аппаратах происходит: 1) конденсация пара в

греющей камере, 2) передача тепла от пара через поверхность нагрева и сло

загрязнений к кипящей жидкости; 3) испарение или кипение жидкости, в ре-

зультате которых выделяются пары растворителя и увеличивается концен-

трация раствора; 4) отделение паров чистого растворителя от жидкости и се-

парация пара. Корректное математическое описание производится на основе

рассмотрения этих процессов во взаимосвязи, т.е. в виде системы уравнений,

описывающих отдельные ст

адии. В свою очередь выпарной аппарат может

рассматриваться как система, состоящая из следующих основных элементов:

греющей камеры, поверхности нагрева, парожидкостного пространства. Для

каждого элемента записываются уравнения сохранения с соответствующими

условиями однозначности, уравнения состояния рабочих тел и ряд эмпириче-

ских зависимостей, учитывающих специфику процессов выпаривания [17].

Стохастическое описание основано на применении методов теори

и веро-

ятностей и математической статистики [5], [9], [10], [13]. Исследуемый объ-

ект характеризуется вектором случайных факторов, определяющих целевую

функцию или выходные параметры. Обрабатывая экспериментальные дан-

ные, определяют коэффициенты зависимости между входными и выходными

параметрами процесса.

Так, в наиболее общем виде, проблема оптимального развития, реконст-

рукции тепло - энергоснабжающих систем и обеспечения их надежности со-

стоит в определен

ии направлений рационального изменения структуры сис-

тем по мере роста эксплуатационных нагрузок и изменения других условий;

в выявлении образования в процессе развития «узких мест» и их устранении

заменой (усилением) некоторых существующих элементов (источников теп-

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

ла, участков тепловых сетей, насосных станций); в определении конкретной

структуры и параметров системы [7-10].

Трудности решения данной проблемы связаны с необходимостью одно-

временного учета свойств тепло – энергоснабжающих средств как сложных

систем (непрерывности развития, неопределенности исходных данных, на-

дежности), их физико-технических свойств (нелинейности гидравлических и

экономических характеристик элементов, существующего состояния систе-

мы, ограничений на параметры режима, дискретности ти

поразмеров обору-

дования, рельефа местности и т.п.); сетевой постановки проблемы.

Математическое описание типовых процессов обычно выражается опре-

деленным классом уравнений. Это позволяет часто формализовать процесс

его составления и существенно облегчает задачу разработки алгоритмов. В

теории дифференциальных уравнений различают корректно поставленные

задачи, т.е. задачи, решени

е которых существует и единственно в некотором

классе начальных и граничных условий и непременно зависит как от этих ус-

ловий, так и от коэффициентов уравнений.

Различают непрерывный и периодический способы организации процес-

са. Периодический процесс характеризуется тем, что параметры состояния

изменяются во времени от некоторого начального до конечного состояния.

Для процессов с сосредоточенными параметр

ами, т.е. при изменении послед-

них только во времени, применяются обыкновенные дифференциальные

уравнения, а для процессов с распределенными параметрами, когда измене-

ние последних происходит во времени и в пространстве (например, измене-

ние концентрации реагента во времени и по длине аппарата), применяются

уравнения в частных производных.

Непрерывный процесс характеризуется тем, что сырье (например, котло-

вая вода) поступает, а продукты (пар или вода) отбираются непрерывно с по-

стоянной скоростью. Технологический процесс при непрерывном способе

организации проце

сса может протекать в стационарном или динамическом

режиме.

Для математического описания непрерывных процессов используются

дифференциальные и конечные уравнения. Первые из них применяются при

описании процессов в динамическом режиме работы и в стационарном с рас-

пределен

ными параметрами. Алгебраические уравнения применяются для

описания непрерывных процессов в стационарном режиме с сосредоточен-

ными параметрами.

Например, в контактных теплообменниках протекают как установившие-

ся, так и неустановившиеся гидродинамические процессы (в пусковых и пе-

ременных режимах, при нестационарном воздействии внешних сил и т.д.)

Возможна реализация противоточного, прямоточного, перекрестного движе-

ния теплоносителей, а также различных комбинаций указанных видов дви-

жения [17].

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

На этом этапе определяющая роль переходит к математику. Для того что-

бы получить единственное решение, которое является основой любого тех-

нологического процесса, нужно выбрать соответствующий тип уравнения

(или системы) и задать необходимые условия.

1.3. Алгоритмизация математического описания объекта

После составления математического описания и конкретизации соответ-

ствующих начальных и граничных условий необходимо выбрать метод ре-

шения, который наиболее пр

игоден в данном конкретном случае.

Используются следующие основные группы методов: качественные, ана-

литические и численные [18-23], [27-30].

Качественные методы позволяют в ряде случаев, например, с помощью

теории подобия, оценить порядок искомой величины или вид функциональ-

ной связи основных параметров[27-30].

При использовании аналитических методов решение задачи удается вы-

разить с пом

ощью формул. В частности, если математическая задача состоит

в решении простейших алгебраических или дифференциальных уравнений,

то использование известных из курса высшей математики приемов сразу

приводит к цели. К сожалению, такие случаи редко встречаются на практике.

На практике приходится иметь дело с задачами, зависящими от одного

или нескольких параметров, начальных данных и т. п., которые лежат в не

ко-

торых интервалах своего изменения.

Для одних параметров, возможно, удается применить аналитический ме-

тод решения, для других – качественный, для третьих – численный метод.

Наилучший эффект достигается при сочетании всех рассмотренных подхо-

дов. Во-первых, результаты применения должны совпадать с учетом точно-

сти вычислений в общей области действия методов; это хороший контроль

правильности проведённых вычислен

ий. Во-вторых, к любой задаче следует

подходить по принципу «сверху вниз», так же, как в алгоритмизации и про-

граммировании. Сначала математическая задача изучается качественными

методами, затем - аналитическими, далее - приближенными и, наконец, чис-

ленными методами.

Перед тем как применить численные методы к задаче, в пособии [24

] ре-

комендуется ответить на следующие вопросы:

1. Какая «ближайшая» задача решается аналитически.

2.Нельзя ли рассматриваемую задачу считать возмущенной «близкой»,

решаемой аналитически.

3.Какая «ближайшая» задача решается успешно численно и каким мето-

дом.

Конкретная техническая задача при своей математической формулировке

записывается в виде соотношений, которые содержат переменные, константы

в обозначениях и размерност

ях, принятых в той области техники, к которой

эта задача относится. Однако в размерных переменных трудно обнаружить,