Голдаев С.В., Ляликов Б.А. Основы математического моделирования в теплотехнике

Подождите немного. Документ загружается.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

тегрирования, т.к. первообразную не удается выразить через элементарные

функции; 2) значения подынтегральной функции известны только в фикси-

рованных точках x

, т.е. она задана в табличном виде, как и в рассмотренных

выше Гл. 2 и 4.

В первом случае для приближенного вычисления интеграла используется

способ представления подынтегральной функции в виде ряда Тейлора [20],

[23], [36]. Это позволяет свести вычисление интеграла от сложной функции к

интегрированию многочлена, представляющего первые несколько членов ря-

да.

Пример. 5.2. При решении задачи о распределен

ии лучистой энергии, ис-

пускаемой абсолютно черным телом по отдельным частотам или длинам

спектра, для интенсивности энергии получено следующее выражение [41]:

()

1exp

∫

∞

−

⎟

⎠

⎞

⎜

⎝

⎛

hcTB

λλ

где h, k - постоянные Планка и Больцмана, с – скорость распространения

электромагнитных волн в свободном пространстве, λ - длина волны, T – тер-

модинамическая температура.

С целью упрощения последующих выкладок вводится новая перемен-

ная (безразмерная температура), после чего выражение принимает вид:

()

1exp

∫

∞

−

duu

Интеграл точно определить невозможно. Приближенное вычисление

осуществляется следующим образом. Знаменатель подынтегральной функ-

ции разлагается в ряд:

()

() ( ) ( ) ( )

∑

∞

−=+−+−+−≅

−

exp...3exp2expexp

1exp

nuuuu

и проводится почленное интегрирование.

Каждое слагаемое представляет собой табличный интеграл [36]:

() ()

expexp

432

nnn

nudunuu =

⎟

⎠

⎞

⎜

⎝

⎛

−+−−−=−

∞

∫

Поэтому можно записать:

()

6exp

∑

∫

∑

∞

=−

dunuu

Известно, что сумма этого ряда равна [36]:

∑

∞

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Окончательно получаем:

()

5.2. Численное интегрирование

Более универсальными средствами, которые пригодны для обоих случаев,

являются методы численного интегрирования, суть которых состоит в замене

подынтегральной функции f(х) на вспомогательную, интеграл от которой

легко вычисляется в элементарных функциях [18], [20], [22], [23], [32]. Гео-

метрически значение определенного интеграла (5.1) представляет площадь,

ограниченную графиком функции )(

, осью абсцисс и прямыми x = a; x

= b. Использование для вычисления величины интеграла квадратурной фор-

мулы означает следующее. Отрезок интегрирования [a, b] разбивается на n

интервалов [ х

, х

i+1

], i = 0, 1, ..., n - 1. Приближенно определяются значения

площадей, соответствующих каждому интервалу, сумма которых дает при-

ближенное значение интеграла.

В зависимости от способа разбиения отрезка интегрирования [a, b] непре-

рывной системой точек (узлов интерполяции) х

, i = 0, 1..., n , различают два

подхода к построению квадратурных формул. При первом варианте местопо-

ложение и длина интервалов разбиения выбираются заранее в начале расче-

тов. Для равноотстоящих точек х

= х

+ i h, i = 0, 1, ..., n; h = (b - a)/n; х

= а;

= b квадратурные формулы называются формулами Ньютона - Котеса. Они

различаются степенями используемых интерполяционных многочленов (ме-

тоды прямоугольников, трапеций, парабол).

Например, в модифицированном методе прямоугольников (методе сред-

них) используются значения функции в средних точках элементарных отрез-

ков ( в полуцелых узлах):

() ( )

()

,...,2,1,,2/2/

1112/1

2/1

nixxhhxxxx

xfhdxxf

iiiiiiii

=−=+=+=

−−−−

−

∑

∫

(5.2)

В методе трапеций отрезок интегрирования [a, b] разбивается на n равных

интервалов длиной h = (b - а)/n. В пределах каждого интервала [х

, х

i+1

]

функция f(х) заменяется интерполяционным многочленом Лагранжа первой

степени с узлами х

, х

i+1

, что соответствует замене кривой на секущую. Зна-

чение интеграла в пределах [х

i+1

], равное площади криволинейной фигу-

ры, заменяется площадью трапеции. Суммирование всех участков разбиения

дает общую площадь, т. е. приближенное значение интеграла:

() () () ( ) ( ) (

)

[

{

hbfhafhafbfaf

dxxf

−+++++++=

∫

...22

(5.3)

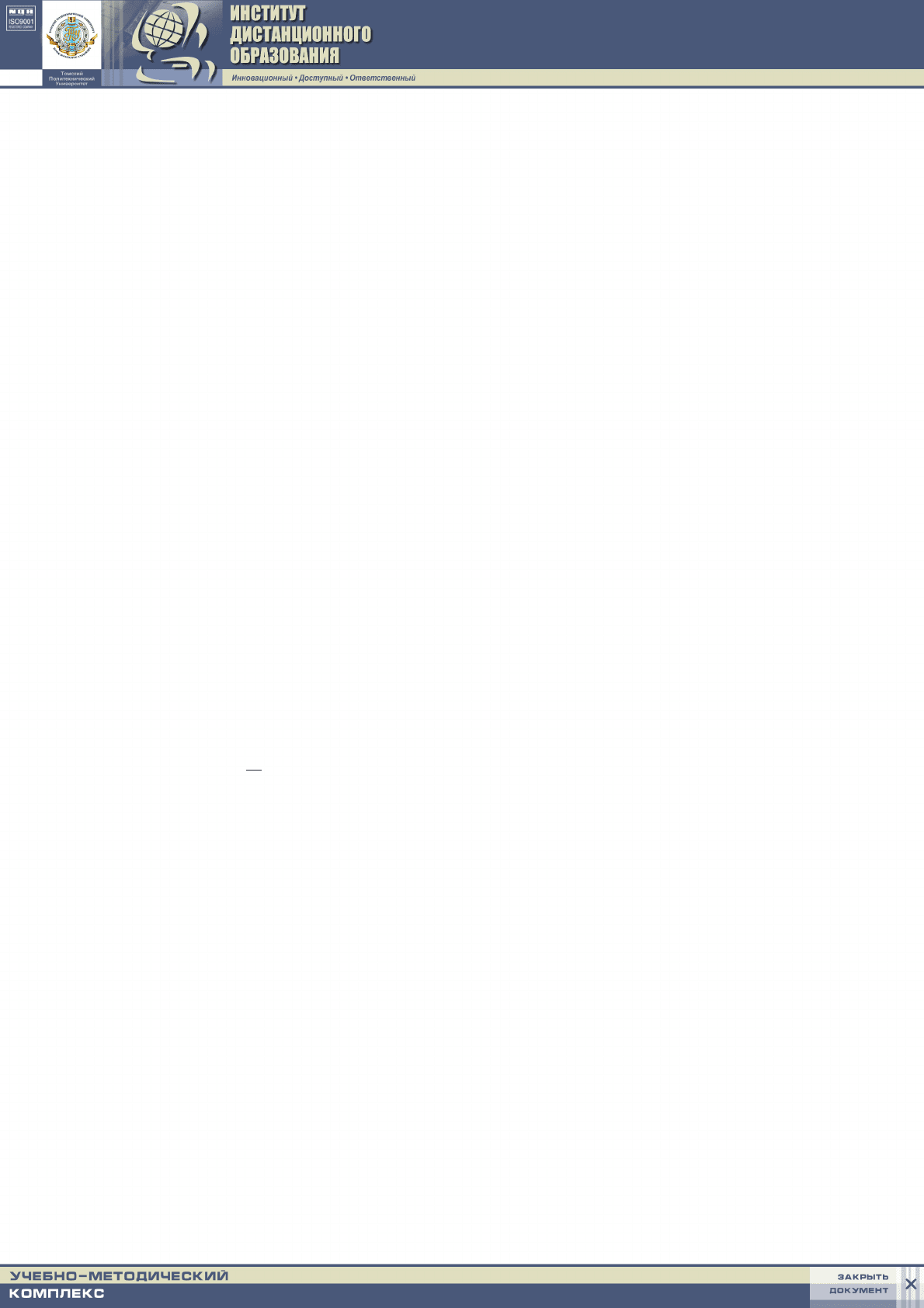
Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Используя значения интегралов, найденных по методам средних и трапе-

ций, можно уточнить значение интеграла следующим образом:

(

)

3/2

III

≅

(5.4)

В соответствии с формулой Эйткена, расчет проводится последовательно

одним методом три раза при различных шагах разбиения h

, h

, которым

соответствуют значения интегралов I

, I

, причем их соотношения посто-

янны: h

= h

= q (например, при делении шага пополам q = 0,5). Тогда

уточненное значение интеграла вычисляется по формуле

()

(

)

,2/

321

211

IIIIIII +−−−=

(5.5)

а порядок точности используемого метода определяется соотношением

(

)

(

)

[

]

.ln//ln

1223

qIIIIp

−

Погрешность численного интегрирования зависит от шага разбиения от-

резка [a, b]. Однако увеличивать число точек не всегда возможно, например,

если функция задана в табличном виде. В этом случае повышение точности

достигается использованием интерполяционных многочленов высоких сте-

пеней.

Согласно методу Симпсона, подынтегральная функция заменяется интер-

поляционным многочленом Лагранжа второй степени. Выражение для вы-

числения определенного интеграла имеет вид:

()

() ( )

(

)

(

)

[]

()() ()

[]

()

⎭

⎬

⎫

⎩

⎨

⎧

+−++++++

∫

bfhbfhafhaf

hbfhafhafaf

dxxf

2...422

...34

(5.6)

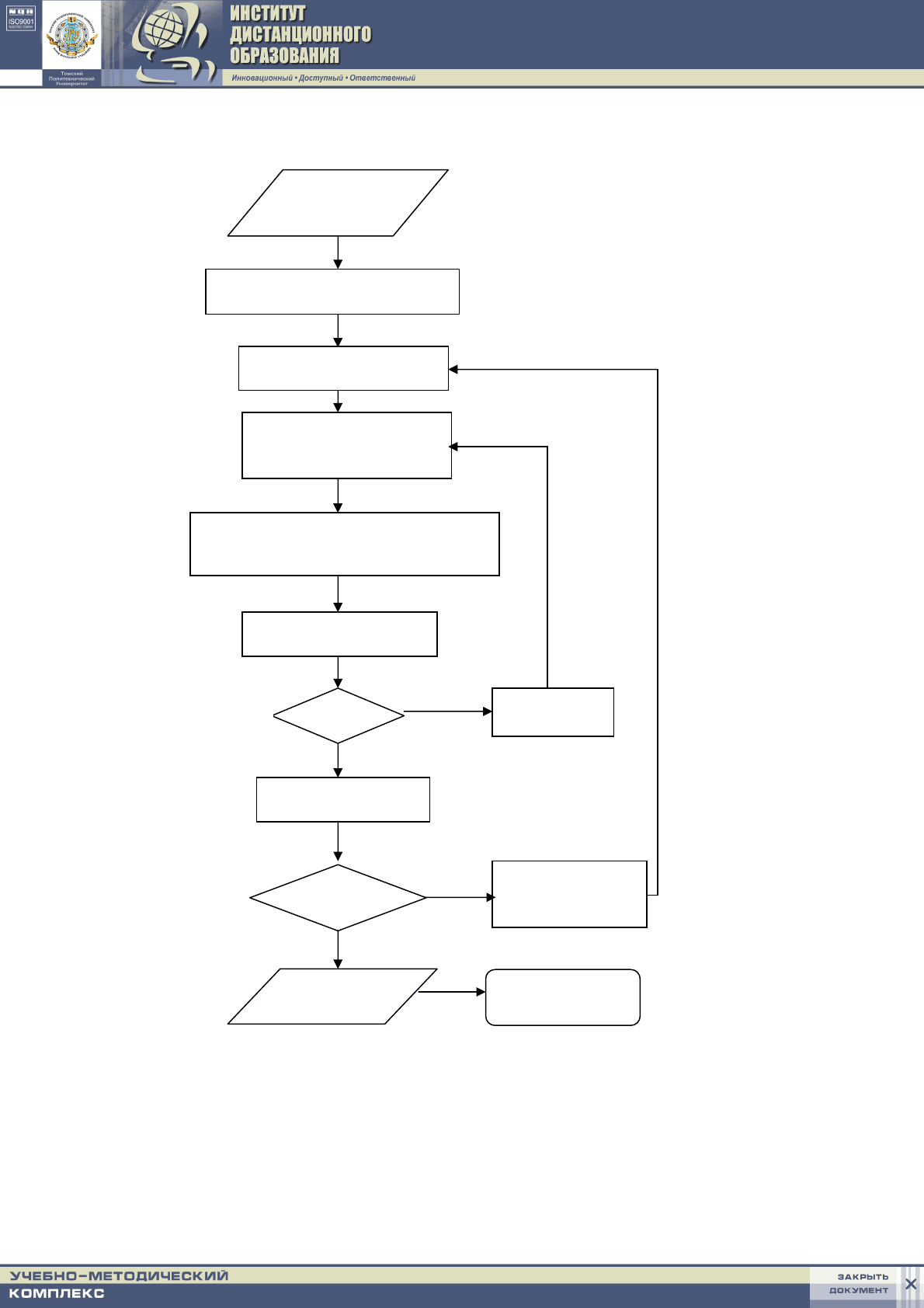
Блок-схема этого алгоритма представлена на рис.5.1.

В качестве исходных значений задаются границы отрезка интегрирования

a, b, погрешность ε, а также формула для вычисления значения подынте-

гральной функции y = f(x). Первоначально отрезок [a, b] разбивается на че-

тыре части с шагом h = (b - a)/4. Вычисляется значение интеграла I

. Затем

число шагов удваивается, вычисляется значение I

с шагом h/2. Условие

окончания счета принимается в виде | I

- I

| < ε. Если это неравенство не вы-

полнено, происходит новое деление шага пополам и т.д.

Формулы (5.4) и (5.6) имеют одинаковую погрешность, однако первая из

них требует двукратного вычисления интеграла разными методами. Кроме

того, для метода Симпсона нужно почти вдвое меньше табличных значений

функции, поскольку для модифицированного метода прямоугольников нуж-

ны дополнительные данные в полуцелых точках.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Из простых способов интегрирования метод Симпсона имеет наиболь-

шую точность, и он приме няется наиболее часто.

Ввод, a,b,

= 0 , n = 4, h = (b-a)/4

= 0, i = 2

= a + ih, x

= x

- h,

= x

- h

=f(x

), y

= f(x

), y

=f(x

S = y

+4y

= I

⋅h/3

i < n

-I

|<ε

Вывод

i = i + 2

= I

, n =n

⋅

h = h/2

Коне

Нет

Да

Рис. 5.1 Блок- схема метода Симсона

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Если порядок используемого интерполяционного многочлена равен шес-

ти, то величина интеграла по формуле Уэддли вычисляется следующим обра-

зом:

() ()

[]

.65

351420

yyyyyy

dxxf

+++++=

∫

(5.7)

При вычислении интегралов с бесконечной границей, являющихся несоб-

ственными, используются специальные приемы.

Так, для интеграла вида

()

∞<<

∫

∞

adxxf

(5.8)

вводится замена переменной x = a/(1- z), которая превращает интервал интег-

рирования [a, ∞) в отрезок [0, 1]. При этом подынтегральная функция и пер-

вые ее производные до некоторого порядка должны оставаться ограничен-

ными.

Другой алгоритм состоит в том, что бесконечная граница заменяется не-

которым достаточно большим числом b так, чтобы принятое значение инте-

грала отличилось от исходного на некоторый малый остаток.

Пример 5.3. При теплофизических измерениях широко применяют

ся изо-

термические тепловые воздействия, когда температура какого-либо слоя ис-

следуемого образца изменяется скачком и сохраняется постоянной на протя-

жении всего теплового процесса [43]. В качестве теплового источника при

этом используется массивное металлическое тело, приведенное в хороший

(идеальный) тепловой контакт с рабочим участком поверхности образца.

На на

чальной стадии процесс развивается в зоне, непосредственно приле-

гающей к изотермическому слою, и любой образец сохраняет признаки по-

луограниченной среды.

Математически процесс описывается решением краевой задачи с гранич-

ными условиями первого рода, которое имеет вид [28-30]

()

(

)

(

)

zerftttxt

−

где t

, t

– температуры (начальная и поверхности) образца,

axz 2/= - без-

размерная координата, a – коэффициент температуропроводности,

- время, )(zerf - интеграл ошибок Гаусса.

Эта функция часто используется в задачах нестационарной теплопровод-

ности [19], [21], [27-30], [43], для нее имеются подробные таблицы [29], [30],

[43], очень точные и удобные аппроксимации [44]. В методических целях

приведем различные варианты ее приближенного вычисления.

Как и в предыдущем примере, воспользуемся известным разложением

подынтегральной функции интеграла ошибок в ряд [36]:

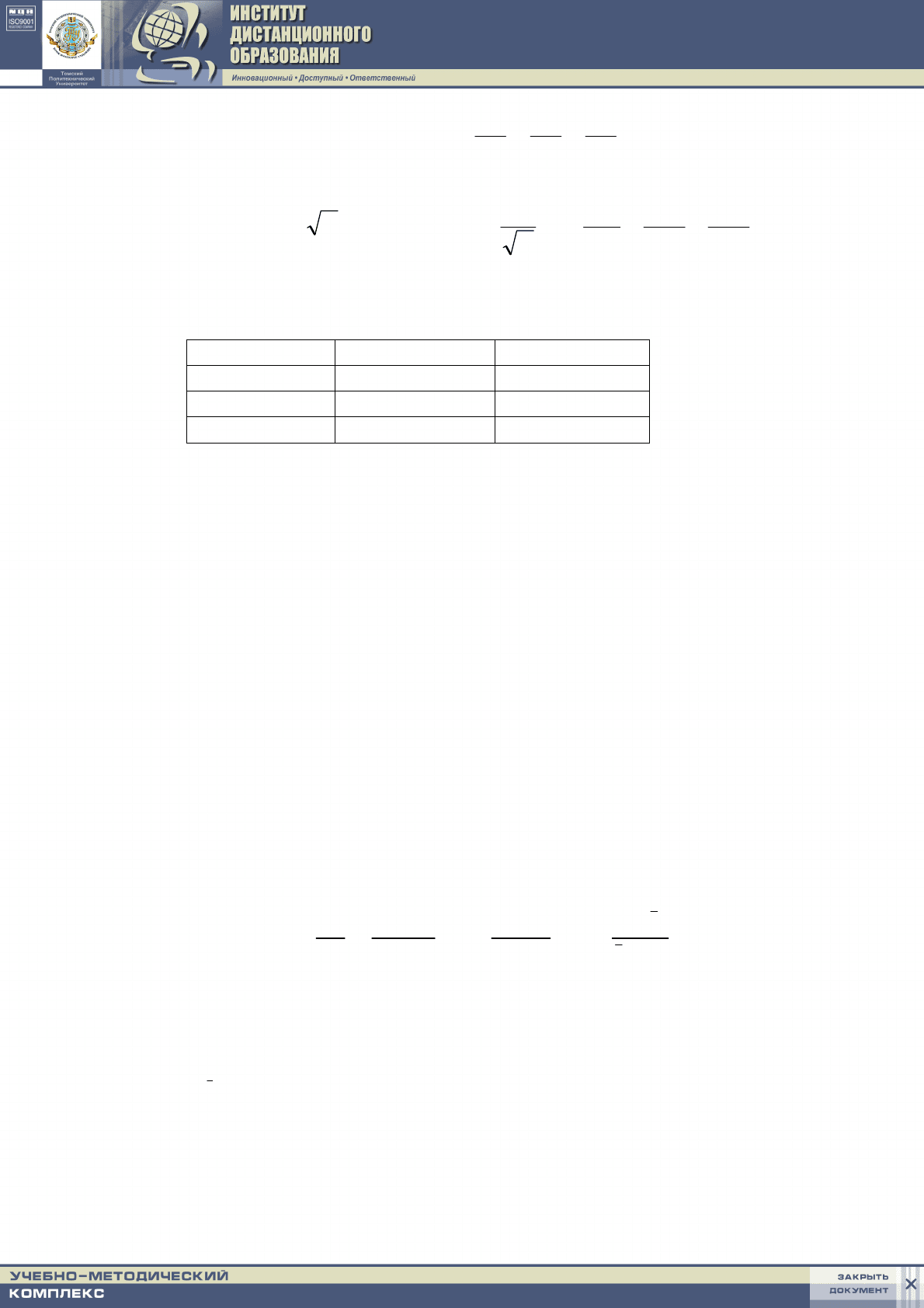
Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

()

...

!3!2!1

1exp

642

+−+−=−

www

Интергрируя почленно данное выражение, получаем

()

∫

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

⋅

−≅−=

zzz

zdwwzerf

753

...

!37!25!13

exp/2

С помощью последнего представления, а также, используя метод трапе-

ций, найдем значения erf(1,2), erf(1,6) и сравним их с табличными:

z/erf(z) 1,2 1,6

erf

(z) 0,9003 0,9764

erf

(z) 0,8886 0,7268

erf

(z) 0,9099 0,9761

Как видно из этих результатов, в области умеренных значений аргумента

(вторая колонка) приближенный (третья строка) и численный (четвертая

строка, шаг h = 0,5) методы дают примерно одинаковую погрешность (около

1%), а при больших z ошибка приближенного достигает 25,5%, в то время

как вычисление по методу трапеций обеспечивает прежнюю точность. Ясно,

что использование в разложении подынтегральной функции большего числа

членов р

асширило бы область точного расчета с его помощью.

Пример 5.4. Для определения расходов топлива, рационального исполь-

зования станционного оборудования, а также для технико-экономических

расчетов при проектировании и эксплуатации системы теплоснабжения ис-

пользуется график продолжительности отопительной нагрузки (в относи-

тельных единицах), представленный на рис.5.2. Годовое количество теплоты,

отпускаемое от источника теплоснабжения, определяется площадью под кри-

вой на этом рисунке, которая построена по зави

симости [45]

−= BNR

;

−

=Θ

−

где R

- отношение тепловой нагрузки при данной температуре наружного

воздуха t

к расчетной тепловой нагрузке на отопление; N - относительное

число часов (суток), при котором относительный расход тепла не бывает

меньше R; B, Q - постоянные коэффициенты, зависящие от климатических

условий;

, tt

- расчетная температура наружного воздуха для проектирова-

ния систем отопления и средняя температура за отопительный период.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Рис. 5.2. График продолжительности отопительной нагрузки.

Площадь можно определить непосредственно по графику (планиметриро-

ванием), либо численным интегрированием (методами прямоугольников,

трапеций или Симпсона). Рассмотрим применение последнего из перечис-

ленных алгоритмов для решения этой задачи. Ниже представлены файлы с

программой, исходными данными и результатами вычислений интеграла ме-

тодом Симпсона, соответственно.

program simpson;

uses Uchism2;

var a,b,sim : real; n : integer;

begin

assign(finp,’c:\tp55\st\G6A54\dsimp.dat’);

reset(finp);

assign(fout,’c:\tp55\st\G6A54\rsim

p1.dat’);

rewrite(fout);

readln(finp,a,b,n); { a,b - пределы интегрирования; n - шаг интегри-

рования }

simp(a,b,n,sim);

writeln(fout,’ Определение годового отпуска теплоты’);

writeln(fout,’ в относительных единицах ‘);

writeln(fout,’ методом Симпсона : ‘,sim:9:3);

readln;

close(finp);

close(fout);

end.

Файл исходных данных.

0.000001 1 50

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Файл с результатами вычислений

Определение годового отпуска теплоты в относительных единицах

методом Симпсона : Q = 0,35

Пример 5.5. Согласно теоретическим представлениям о горении полиф-

ракционного факела, оно может происходить в кинетической и диффузион-

ной областях [3]. Связь между неполнотой сгорания кокса G и текущими

размерами частиц разных фракций в кинетической области выражается через

интеграл следующего вида:

()

(

)

(

)

[

]

xymy

mlxI

∫

−

−−−

1exp

Здесь l = 0,8…1,6 – показатель полидесперсности; m = 6,9; x – текущий

относительный размер наиболее крупной частицы; y - отношение начального

размера частицы i-ой фракции к начальному размеру наиболее крупной час-

тицы.

Интеграл изменяется от 1 (в начале факела) до нуля в конце. При l ≠1 он

может быть представлен аналитически с помощью элементарных функций и

гамма-функции Эйлера [36], а при l = 1 – через интегрально-показательну

функцию [44]. Однако выражения получаются громоздкими и неудобными

для инженерных расчетов, поэтому целесообразно определять его численно.

Поскольку области изменения подынтегральной функции и самого инте-

грала невелики, то можно воспользоваться формулой Уэддли (5.7). В частно-

сти, для x = 0,65, l = 1,6, m = 6,9, получаем I

(0,6) ≅ 0,00799. Для контроля ре-

зультата вычисления были выполнены по методу Симпсона (5.6) с шагом h =

0,05 и величина интеграла оказалась равной I

(0,6) ≅ 0,00798.

Пример 5.6. В камере сгорания газотурбинной установки к воздуху под-

водится теплота при постоянном давлении, в результате чего его температура

повышается от T

= 473 К до T

=1073К. Найти подведенное удельное коли-

чество теплоты qp с учетом следующей зависимости истинной теплоемкости

от температуры:

T, K

473 573 673 773 873 973 1073

, кДж/кг

1,024 1,045 1,068 1,092 1,115 1,136 1,155

Как известно из курса технической термодинамики [33],

() ( ) ( )

ThThdTTcq

−==

∫

В нашем распоряжении имеется 7 точек, которым присвоим индексы 0,

1,…, 6. Применяя формулу интегрирования (5.8), получаем:

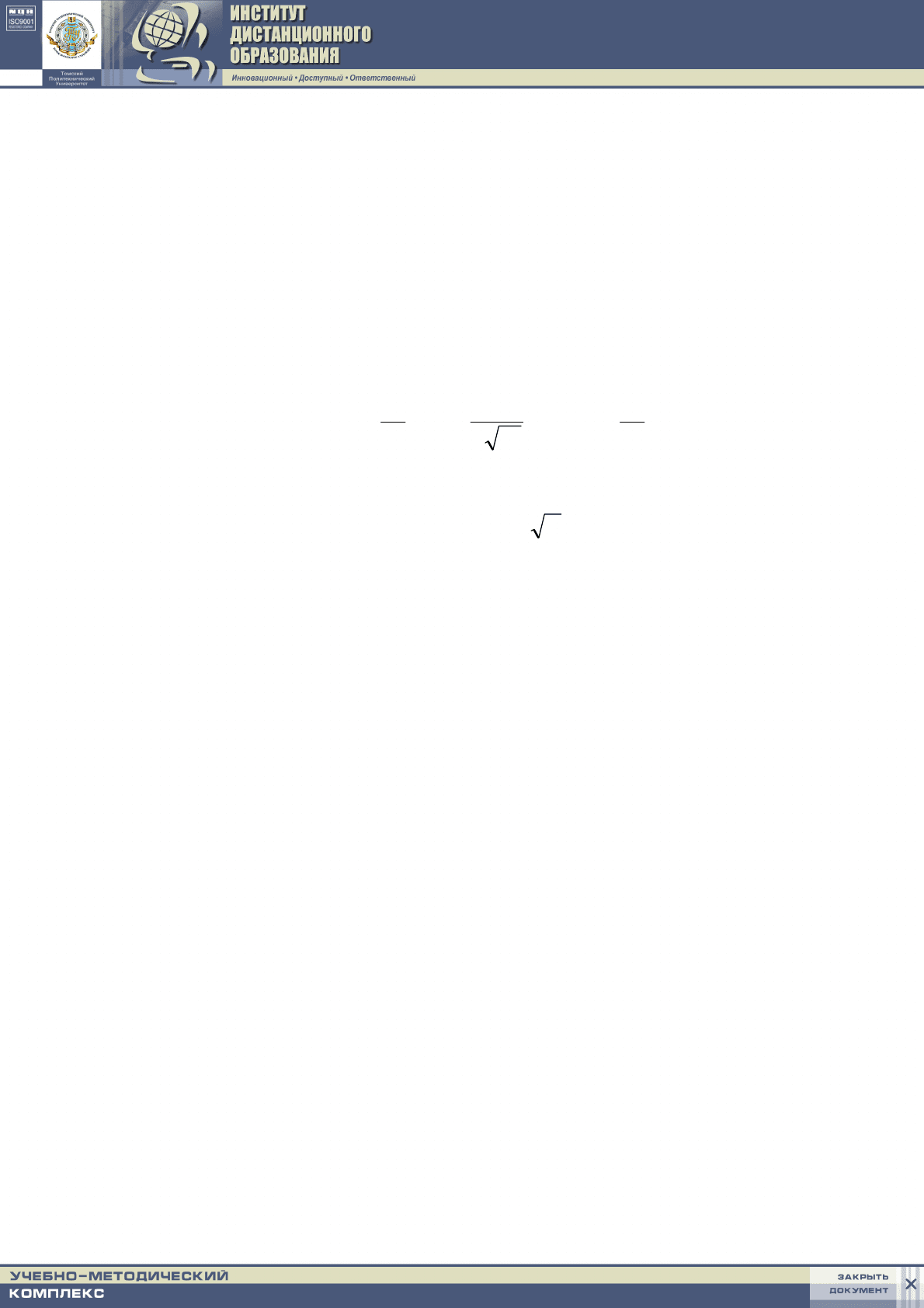
Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Для оценки точности найденного значения подведенного удельного коли-

чества теплоты, вычислим его через разность энтальпий. Используя их таб-

личные значения [35], определяем

()

(

)

4,6544,4758,1129

−

−= ThThq

кДж/кг.

Пример 5.7. Рассмотрим часто применяемый в теплофизических исследо-

ваниях [42] процесс нагрева полуограниченного тела постоянным тепловым

потоком q

, который воздействует на плоскую поверхность. В математиче-

ском плане он моделируется второй краевой задачей, решенной многими

способами [19], [21], [27-30], [41], [43]. Профиль температуры тела в любой

момент времени описывается следующим выражением:

() ()

wierfc

Tdx

erfc

TtxT

λλ

⎟

⎠

⎞

⎜

⎝

⎛

∫

∞

где erfc(w) = 1- erf(w) – дополнительный интеграл вероятностей.

Интеграл от функции ошибок имеет вид:

()

(

)

(

)

./exp

werfcwwwierfc ⋅−−=

Он также часто встречается в задачах теплопроводности, для него имеют-

ся подробные таблицы [43], [44]. В методических целях найдем его значение

методом Симпсона.

Подынтегральную функцию – дополнительный интеграл вероятностей-

будем вычислять с помощью следующего аппроксимационного выражения

из справочника [44]:

() ( )

[]

(

)

(

)

.7478556,0,0958798,0,3480242,0,47047,0

,1/1,exp

3210

321

=−===

+=−++=

kkkk

wkzwzkkzkzwerfc

В примере определялось значение этого интеграла для w = 0,5. Верхняя

граница варьировалась: при b = 2,5 и шаге h = 0,25 была получена занижен-

ная примерно на 8% величина по сравнению с табличными данными; при b =

3,0 совпали четыре цифры после запятой ierfc(0,5) ≅ 0,19962.

Найденная «бесконечность» может использоваться в расчетах для других

w. Данная функция является быстро убывающей: ierfc(0) = 0,5642, ierfc(2,0) =

0,0010. С приближением w к b требуется у

меньшать длину шага.

6. МЕТОДЫ РЕШЕНИЯ СТАЦИОНАРНЫХ ЗАДАЧ

ТЕПЛОПРОВОДНОСТИ

6.1. Одномерные стационарные задачи теплопроводности

Многие процессы теплотехники успешно моделируются в рамках стацио-

нарных краевых задач. Известно, например, что одним из эффективных спо-

собов интенсификации теплопередачи является оребрение стенок. Строгое

аналитическое решение о распространении теплоты в ребре связано со зна-

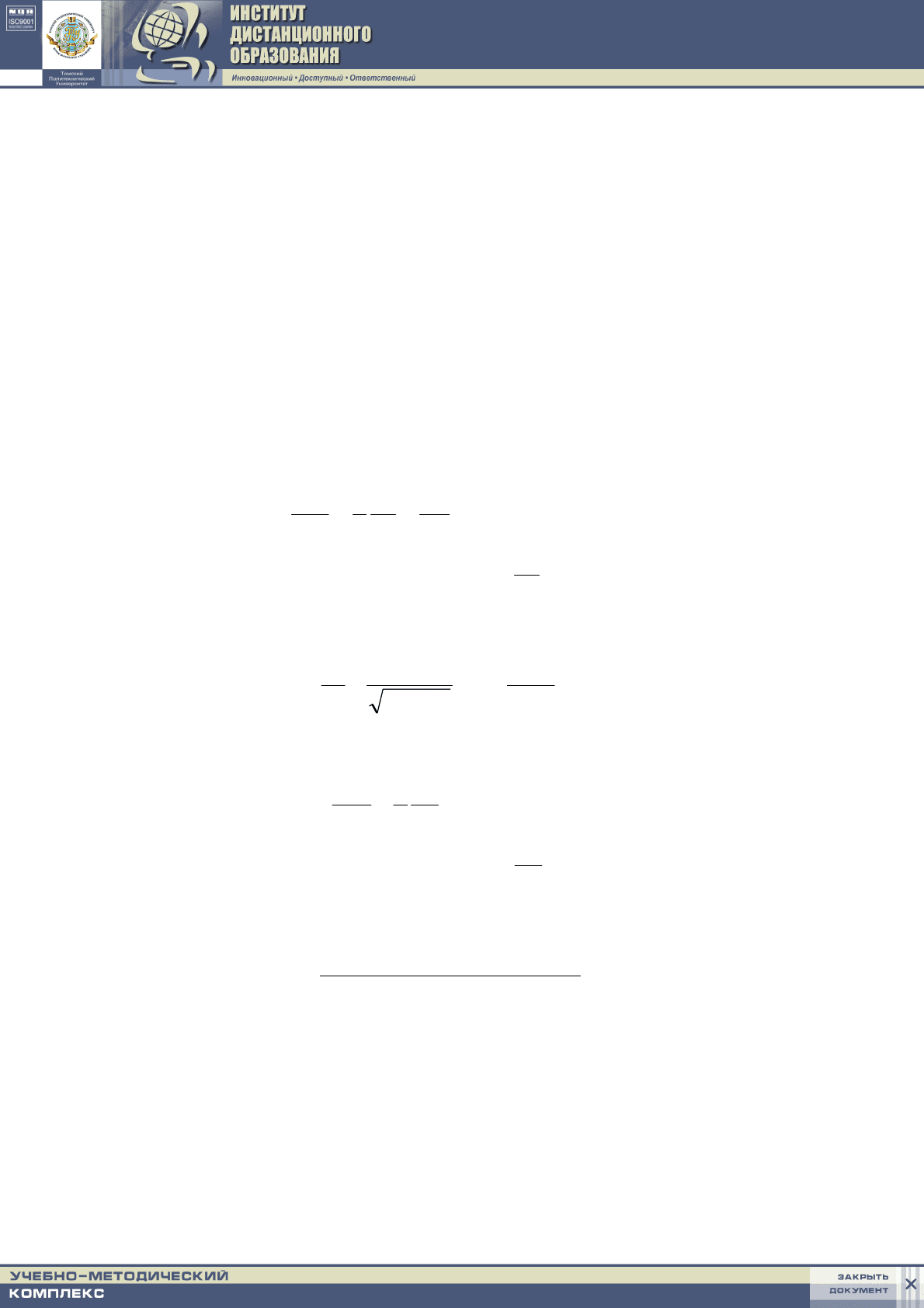
Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

чительными трудностями. В основу решения кладут определенные допуще-

ния, которые позволяют сравнительно простым путем получить нужный ре-

зультат [27-30], [41], [48].

Пример 6.1. Для интенсификации теплоотдачи с цилиндрических поверх-

ностей труб применяются круглые ребра постоянной толщины [28]. Задача

моделируется следующим образом. Известны внутренний r

= 0,02 м и на-

ружный r

= 0,04 м радиусы ребра, выполненного из титана, его толщина δ =

0,002 м; коэффициенты теплопроводности λ =15 Вт/(м.К) и теплоотдачи α =

37,5 Вт/(м2.К) по всей поверхности принимаем постоянными; температура у

основания ребра t

= 110 0С, а также окружающей среды t

= 10 0С считаем

не зависящими от времени. Теплоотдачей с торцевой части круглого ребра

пренебрегаем.

Процесс описывается следующей краевой задачей

()

=−−+

δλ

.0:,: =−===

rrttrr

kff

(6.1)

Перейдем к безразмерным перемененным, определяемым так:

−

===

αδλ

(6.2)

Задача перепишется следующим образом:

=−+ u

.0:,: =−===

zzuuzz

kff

(6.3)

Ее решение имеет вид [28]:

()

(

)

(

)

(

)

()

() ()

()

fkkf

zKzIzKzI

0110

)(

(6.4)

где I

(z), K

(z), I

(z), K

(z) – соответственно функции Бесселя первого и вто-

рого рода нулевого и первого порядка.

Эта формула малоудобна для технических приложений, связанных

с рас-

четом распределения температуры в ребре и на его конце, поскольку необхо-

димо использовать табличные данные для специальных функций [36] либо их

аппроксимации [44].