Голдаев С.В., Ляликов Б.А. Основы математического моделирования в теплотехнике
Подождите немного. Документ загружается.


Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
81
()
() () ()
.:1,:0,:0
,0,10,,
21
2
2
FouzFouzzu
FozFozQ
z
u
Fo
u
ψψϕτ
======
>≤≤+
∂
∂
=
∂
∂
(7.46)
Такая постановка моделирует процесс распределения температуры в
пластинке с источником выделения тепла за счет прохождения электрическо-
го тока, действия ядерных реакций и др. [30].
Перейдем к разностному аналогу этой задачи на равномерной прямоли-
нейной сетке:
()
() ()
.,,
..),1,0;1,...,2,1(,
2
210
0
2
11
1
j
j
kj
j
ii
j
i
j
i
j
i
j
i
j
i
j
i
FouFouzu
jkiQ
h
uuu
Fo
uu
ψψϕ
===
=−=+
Δ
+−
=
Δ
−
−+
+
(7.47)
Разрешая ее относительно верхнего временного слоя, получаем:
(
)
()
./,FoQ 21
2j
i11
1
hFokukuuku
j
i
j
i
j
i
j
i
ΔΔ=Δ+−++=
ΔΔ−+Δ
+
(7.48)
Данная схема имеет первый порядок аппроксимации по времени и вто-
рой - по координате. Она устойчива при выполнении условия k
Δ
≤1/2. При k
Δ
=1/2 получаем особенно простой вид рекуррентных соотношений
(
)
.2/
11
1
j
i
j
i
j
i
j
i
FoQuuu Δ++=
−+
+
(7.49)
В результате получается система алгебраических уравнений для опре-
деления значений сеточной функции во внутренних узлах.
Рассмотрим конкретную задачу.
Пример 7.5 Используя разностное уравнение (7.49), найти приближен-
ное решение краевой задачи
()
.0:1,0:0,sin:0
,0,10,
2
2
======
>≤≤
∂
∂
=
∂
∂
uzuzzuFo
Foz
z
u
Fo
u
π
(7.50)
и сравнить его с точным решением, имеющим вид [43]:
()
(
)
(
)
zFoFozu
a
ππ
sinexp,
2
−=
.
(7.51)
Решение. Выбираем по координате шаг Δh = 0,1. Для обеспечения ус-
тойчивого решения можем использовать шаг по времени ΔFo < (Δh)
2
/2 =
0,005. Значения функции u(z, F
o
) на первом слое находим, используя началь-
ное и краевые условия, по формуле (7.49) при j = 0:
(
)
.2/
0
1
0
1
1
−+
+=
iii
uuu
Таким образом, получаем:
5590,0
2
309,0809,0
2
,2939,0
2
05878,0
2
0
1
0
3
1
2
0
0
0
2
1
=
+
=
+
==
+
=
+
=
uu
u
uu
u
i
и т.д.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
82
Аналогично находим значения на следующем временном слое при j =1:
(
)
.2/
1
1
1
1
2
−+
+=
iii
uuu
Ниже представлен листинг программы решения данной задачи, в кото-
рой использованы две процедуры. Первая из них предназначена для нахож-
дения значений температур по аналитическому решению, а вторая – числен-
ному. Эксплуатация программы производится в диалоговом режиме: после ее
трансляции задаются границы a = 0, b =1, точность e = 0,001, число точек по
оси координат m = 10 и ограничение на проведение счета по безразмерному
времени n = 5.
program yavm
etpl;
uses crt;
type mat = array[0..33,0..33] of real;
const pi=3.1415926;
var a,b,e,dh,dt,x,ua,t,fi:real; l1,m,n,i,j:integer; f1,f2:mat;
procedure an(a,b,x,t:real; var ui:real);
begin
for i:=0 to m do
begin
x:=i*dh; for j:=0 to n do
begin
t:=j*dt; ui:=exp(-sqr(pi)*t)*sin(pi*x);f1[i,j]:=ui;
end
end
end;
procedure fch( m,n:integer);
var i,j,k:integer;
begin
for i:=0 to m do f2[i,0]:=sin(pi*i*dh);
for j:=0 to n-1 do
begin
f2[0,j]:=0; f2[m,j]:=0; for i:=1 to m-1 do
begin
f2[i,j+1]:=(f2[i-1,j]+f2[i+1,j])/2;
end;
end;
end;
begin
clrscr;
repeat
write ('a,b,e,m,n '); readln(a,b,e,m,n);
dh:=b/m;dt:=sqr(dh)/2; an(a,b,dh,dt,fi); fch(m,n);
writeln(' - «analit. chislen');
for i:=1 to (m-1) div 2 +1 do
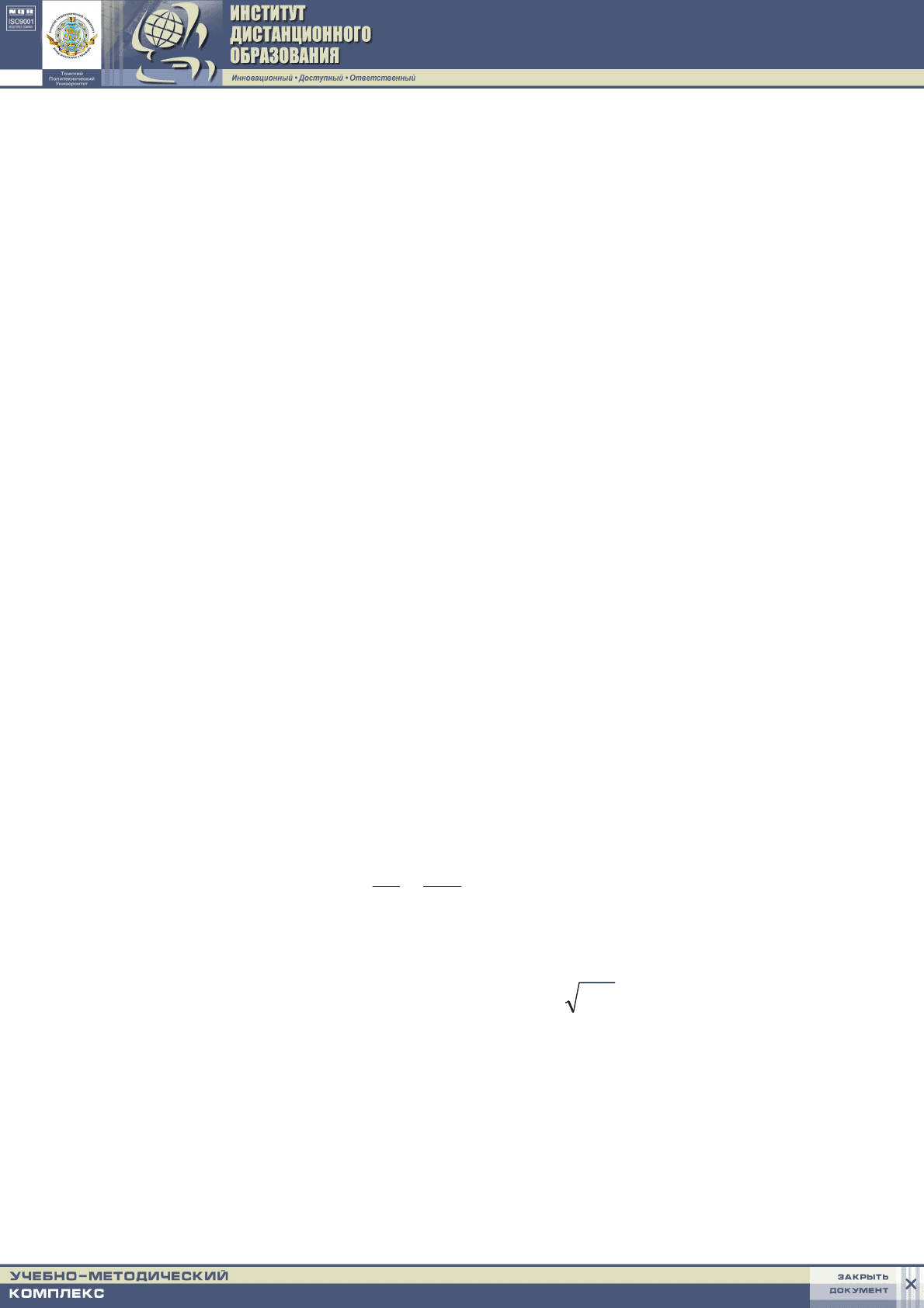
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
83
begin
writeln('x=',i*dh:5:3);
for j:=1 to n do
if j mod 2 = 1 then writeln(' t=',j*dt:5:3,' ua=', f1[i,j]:5:3,' un=',f2[i,j]:5:3)
end;
until readkey =#27
end.
Результаты аналитического и численного решений задачи приведены ниже.
a,b,e,m,n 0 1 0.001 10 5
analit. chislen
x=0.100
t=0.005 ua=0.294 un=0.294
t=0.015 ua=0.266 un=0.266
t=0.025 ua=0.241 un=0.240
x=0.300
t=0.005 ua=0.770 un=0.769
t=0.015 ua=0.698 un=0.696
t=0.025 ua=0.632 un=0.629
x=0.500
t=0.005 ua=0.952 un=0.951
t=0.015 ua=0.862 un=0.860
t=0.025 ua=0.781 un=0.778
Хорошее совпадение значений безразмерных температур подтверждает
правильность выбора алгоритма и составления программы.
Пример. 7.6. В строительной теплофизике возникает необходимость вы-
бора требуемой толщины кирпичной кладки стены, определения глубины
прокладки трубоп
роводов и т.п. [41], которые находятся под воздействием
периодически изменяющейся температуры среды (суточной, сезонной ). Та-
кой процесс моделируется следующей краевой задачей:
()
,0:,sin:0,0:0
,0,0,
2
2
=∞→====
>∞≤≤
∂
∂
=
∂
∂
uzuzu
Foz
z
uu
ωττ
τ
(7.52)
где
()
−===Δ−=
000
/2,/,/,/
τπτωττττ
rrc
axztttu
соответственно безразмерные температура, время, координата и частота
колебаний;
t
c
, Δt – среднее значение температуры поверхности и амплитуда ее ко-
лебаний;
τ
0
– период колебаний.
Точное решение сформулированной задачи получено в [30] и имеет вид:
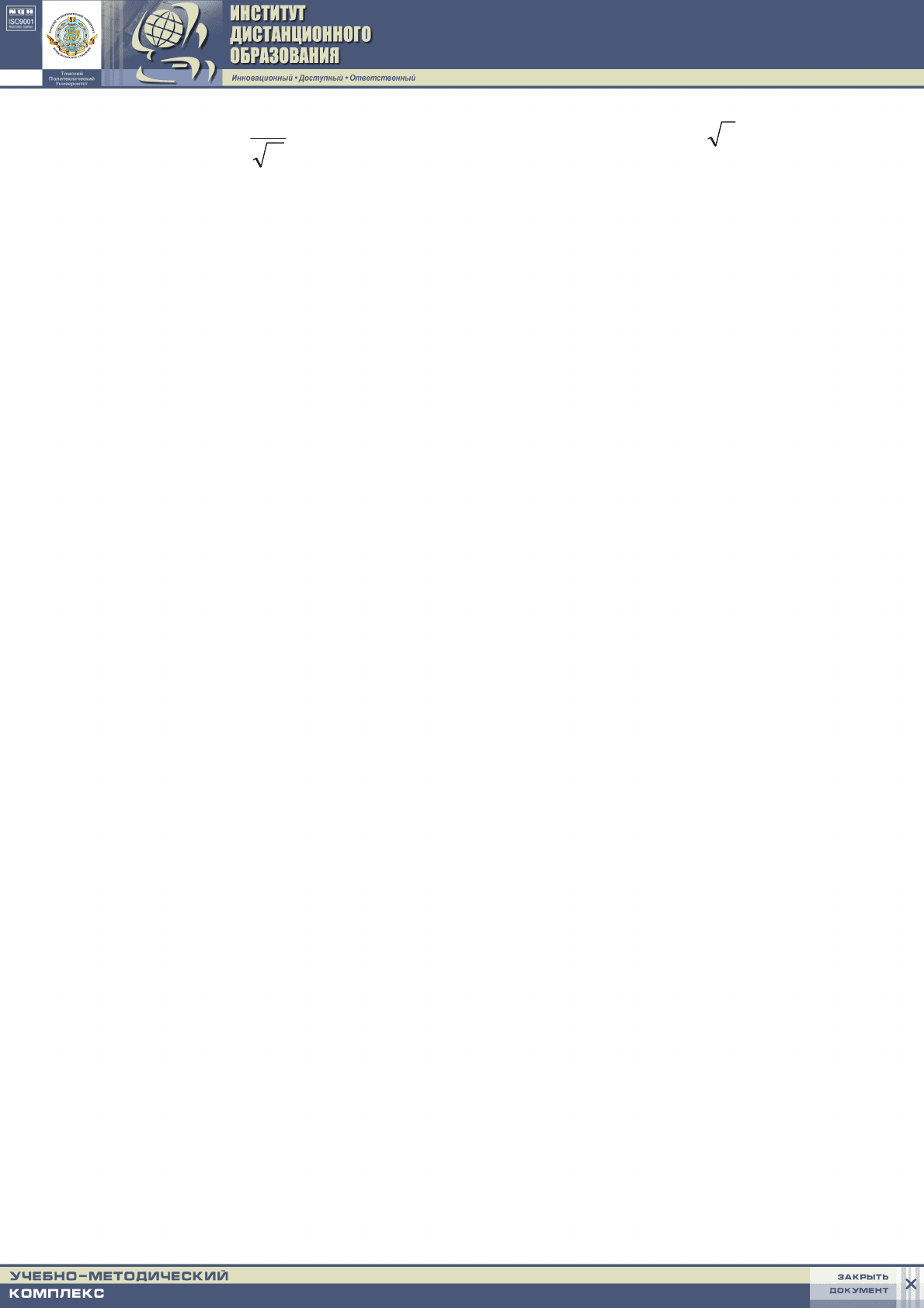
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
84
()
[]
{}
()
τξξξτω
π
2/,exp2/sin
2
2
2
zwdzu
w
a
=−−=
∫
∞
(7.53)
Для численного решения краевой задачи необходимо модифицировать
программу, представленную выше. Вычисление температуры по аналитиче-
ской формуле осуществим с помощью программы, реализующей метод Сим-
сона (гл.5), поэтому первую процедуру убираем из описания. В процедуру
явного метода вносим небольшие изменения, учитывающие соответствую-
щие начальное и граничные условия.
program yavmetpl_d;
uses crt;
type mat = array[0..75,0..50] of real;
const pi=3.1415926;
var a,b,e,dh,dt,x,ua,t,fi:real; l1,m,n,i,j:integer;
f1,f2:mat;
procedure fch( m,n:integer);
var i,j,k:integer;
begin
for j:=0 to n do f2[0,j]
:=sin(2*pi*j*dt);
begin
f2[i,0]:=0; f2[m,j]:=0;
for j:=0 to n do
for i:=1 to m do
begin
f2[i,j+1]:=(f2[i-1,j]+f2[i+1,j])/2;
end;
end;
end;
begin
clrscr;
repeat
write (' a,b,e,m,n ');
readln(a,b,e,m,n);
dh:=(b-a)/m; dt:=sqr(dh)/2;
fch(m,n);
writeln(' analit. chislen');
for i:=0 to m-74 do
begin
writeln( ' x=',i*dh:5:3);
for j:=1 to n do
if j mod 5 = 1 then writeln(‘ t= ‘, j*dt:5:3,
{' ua=', f1[i,j]:5:3,}' n=',f2[i,j]:5:3)
end;
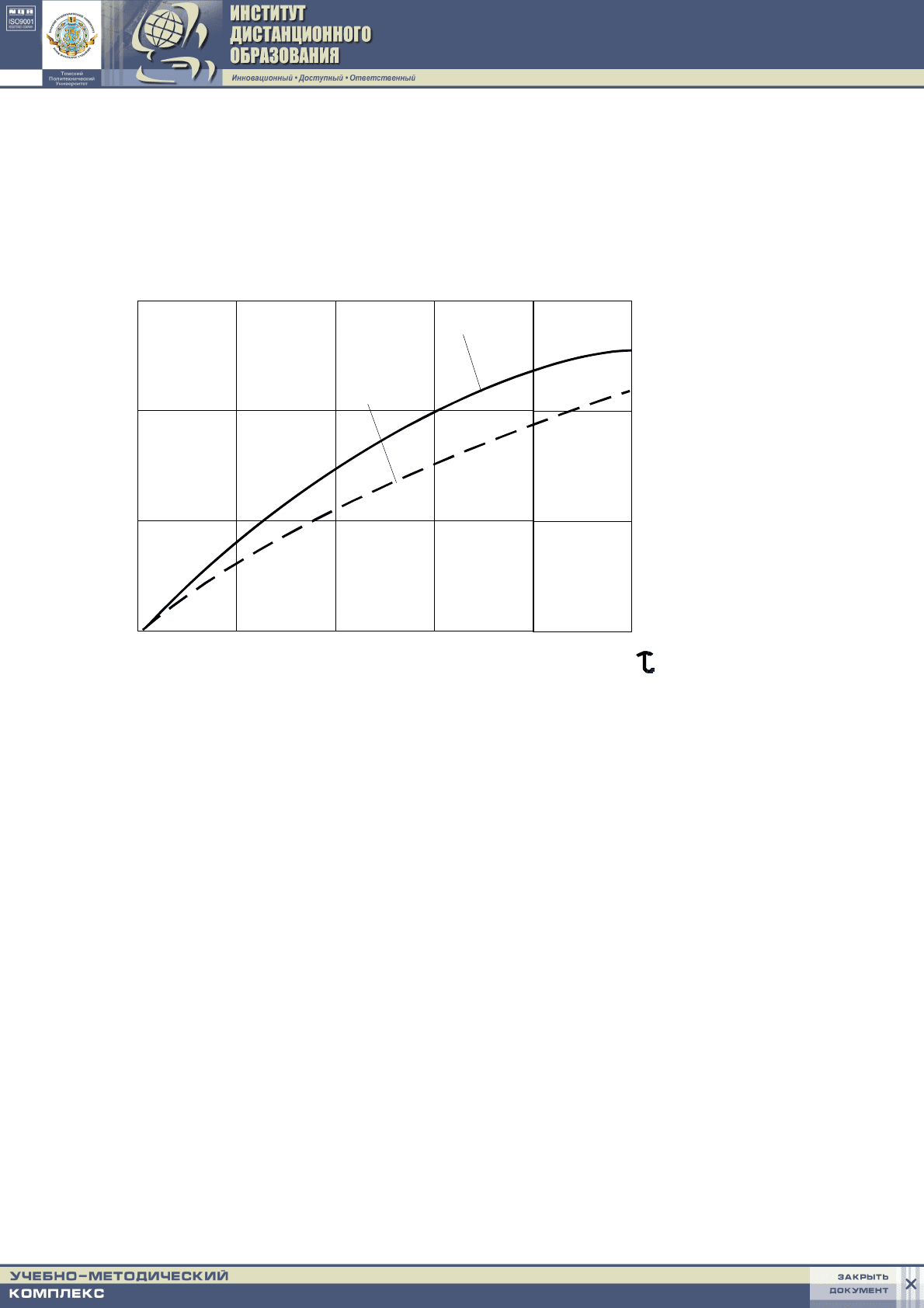
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
85
until readkey =#27
end.
На рис. 7.7 представлены результаты расчета безразмерной температу-
ры, полученные разностным методом (пунктирная кривая) и на основе точ-
ного решения (отмечены треугольниками).
Рис. 7.7. Зависисмость безразмерной температуры на поверхности
и в глубине полуограниченного стержня при периодическом
нагреве его торца
8. ПРИМЕРЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ В ПРО-
МЫШЛЕННОЙ ТЕПЛОТЕХНИКЕ
8.1. Математическая модель процесса
самовоспламенения угольной пыли
Физическая постановка задачи. Имеется цилиндрическая камера, темпе-
ратура которой поддерживается равной начальной температуре топливовоз-
душной смеси [4]. Частицы топлива имеют сферическую форму; во входном
сечении камеры скорость и температура пылевых частиц одинаковы со ско-
ростью и температурой в потоке; частицы в потоке распределены равномер-
но, и дисперсность их известна. Поскольку в угольной пыли обыч
ной тонко-
сти основную массу составляют мелкие фракции, то можно считать, что тем-
пература и скорость реагирующих пылевых частиц мало отличается от тем-
пературы и скорости газа, т.е. в ходе реагирования температура газа повыша-
ется вместе с температурой частиц. Процесс воспламенения развивается в
0,80
0,40
0,00
u
0 0,05 0,10 0,15 0,20
х =0.1
х =0

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
86
кинетическом режиме горения. При расчете выхода и выгорания летучих
компонент для кинетических констант приняты их эффективные значения.
Развитие процесса самовоспламенения проявляется изменением по дли-
не камеры трех параметров: роста температуры и уменьшения концентраций
угольной пыли и кислорода и материального баланса по расходу угольной
пыли.
Математическая постановка задачи.
1. Уравнение теплового баланса р
еагирующей смеси
0
=
−
−
thp
dQdQdQ
(8.1)
показывает, что теплота, выделяющаяся при химическом реагировании в
смеси в элементарном объеме dQ
p
, расходуется на нагрев смеси dQ
h
и час-
тично отводится в окружающую среду dQ
t
.
При равномерном распределении угольной пыли в пылевоздушной сме-
си для тепловыделения в элементарном объеме на участке камеры dx можно
записать выражение:
,
4
exp
2
2
0
0
dx
d
fQ
T
T
C
TR
E
kdQ
rr
u
p
π
μβ
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
(8.2)
где β - стехиометрический коэффициент; k
0
exp(-E/R
μ
T) – константа ско-
рости реакции, м/с; E – энергия активации, кДж/моль; R
μ
= 8,314 – универ-
сальная газовая постоянная, кДж/(моль⋅К); T – текущая температура смеси,
К; С
r
и μ
r
- текущие значения концентрации кислорода и пыли, кг/м3 при
давлении 0,1013 МПа и температуре 293 К; f и Q - соответственно поверх-
ность, м
2
/кг и теплота сгорания, кДж/кг угольной пыли; d – диаметр камеры,
м.
Перейдя в выражении (8.2) к безразмерным температуре, концентрациям
кислорода и топлива, определяемым в виде
,,,
00
μ
μ
μ
rr
u
C
C
C
E
TR
===Θ
(8.3)
получим:
,
1
exp
4
2
2
0
2
000
dxC
E
RT
d
fQCkdQ
u
p
⎟
⎠
⎞
⎜
⎝
⎛
Θ
−
Θ
⎟
⎠
⎞
⎜
⎝
⎛
=
μπ
μβ
(8.4)
где μ
0
и С
0
– начальные значения концентраций пыли и кислорода.
Расход теплоты на нагрев смеси составляет
,dx
dx
dT
VcdQ
mmh
=
(8.5)

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
87
где
44
2
0
0
2
d
w
T
T
d
wV
m
ππ
==
- секундный расход смеси, м
3
/с; w
0
– скорость,
м/с при начальной температуре T0 =273 К;
dadam
ccccc ,,
0
μ
+
=
- соответст-
венно теплоемкости смеси, воздуха и пыли, кДж/(м
3
⋅К).
Подставив в (9.5) выражения для объема и теплоемкости смеси, после
перехода к безразмерной температуре получаем:
()
.
4
2
00
dx
dx
dd
R
ccEw
dQ
u
da
h
Θ
+
=
π
μ
(8.6)
Теплоотвод по закону Ньютона, представляем как
() ()
,dx
R
E
ddxTTddQ
s
u
csct
Θ−Θ=−=
παπα
(8.7)
где α
c
- коэффициент теплоотдачи между реагирующей смесью и стенкой
камеры, имеющей температуру Ts .
Подставив выражения (8.4), (8.6) и (8.7) в уравнение (8.1), разделив на
комплекс постоянных величин первого его члена и отнеся к единице объема
смеси, получаем уравнение теплового баланса реагирующей смеси в безраз-
мерном виде
()
()
,
/1exp
2
s
C
d
d
Θ−ΘΩ−
Θ
Θ
−
=
Θ
μ
ξ
(8.8)
в котором
()
2
0000
2
0
00
000
4
,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=Ω
⎟
⎠
⎞
⎜
⎝
⎛
+
=
uu
u
da
u
RT
E
fdQRCk
E
E
RT
Eccw
fQRCk
x
μβ
α
μ
μβ
ξ
(8.9)
есть безразмерные координата и коэффициент теплоотдачи.
1.Уравнение материального баланса по расходу кислорода, в котором
убыль кислорода в пылевоздушной смеси приравнивается его расходу на хи-
мическое реагирование
2. В этом уравнении удельная скорость реагирования пыли по кислороду
равняется
.
44
22
2
d
fK
d
wC
dx
d
O
c
π
μ
π
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
(8.10)
μμ
(8.11)
Подставив в уравнение (8.10) последнее выражение и перейдя к безраз-
мерным температуре
μ
, концентрациям кислорода и угольной пыли, а также

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
88
учитывая, что из стехиометрического соотношения между расходом топлива
и кислорода существует связь β = 1/(V
0
C
μ
), получаем:
⎟
⎠
⎞
⎜
⎝
⎛
Θ
−
⎟
⎠
⎞
⎜
⎝
⎛
=−
1
exp
2
0
00
0
0
C
E
RT
fQk
dx
dC
V
w
u
μμ
β
,
(8.12)
где V
0
– теоретически необходимое количество воздуха, м3/кг.
Переходя к безразмерной координате, в соответствии с (8.9), получаем
второе дифференциальное уравнение в виде
,
1
exp
20
⎟
⎠
⎞
⎜
⎝
⎛
Θ
−
ΘΘ
−=
a
C
d
dC
μ
ξ
(8.13)
в котором
()
Ecc
QR
da
u
a
0
0
μ
+
=Θ
есть безразмерная адиабатная температура пылевоздушной смеси при T
0
=
273 K.
3. В качестве третьего уравнения в математической модели процесса са-
мовоспламенения используется связь между пропорциональными количест-
вами расхода угольной пыли и кислорода при химическом реагировании:
(
)
.
00
CC
−
=
−
β
μ
μ
(8.14)
Переходя к безразмерным концентрациям и используя соотношения
,
1
,
1
000
0
CVV
==
β
α
μ
получаем третье уравнение системы
(
)
,11 C
−
−
=
α
μ
(8.15)
в котором α - коэффициент избытка воздуха.
Граничное условие формулируется следующим образом:
.1,1,:0
1
=
=
Θ=Θ=
μ
ξ
C
(8.16)
Путем численного интегрирования данной задачи Коши методом Рунге
–Кутта было проведено ее параметрическое исследование и выявлены наи-
более благоприятные условия для развития первичного реагирования, пере-
водящего процесс к высокотемпературному режиму.
На рис.8.1 представлены результаты расчета распределения температур
по координате при фиксированном коэффициенте избытка воздуха (α = 0,1)
и различной интенсивности теплообмена.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
89
Рис. 8.1. Температурные кривые реагирования при
самовоспламенении в одномерном потоке
Как видно, развитие процесса самовоспламенения характеризуется
плавным, со все возрастающим темпом подъема температурных кривых. Рез-
кий взмыв температуры означает наступление самовоспламенения. Значения
координаты ξ
1
, при которой наступает интенсивный подъем температуры,
дают безразмерную длину участка самовоспламенения при начальной без-
размерной температуре Θ
1
и данных значениях Ω и α или, при соответст-
вующем пересчете, – период индукции. С увеличением теплоотвода развитие
процесса замедляется, длина участка самовоспламенения увеличивается, а
максимальная температура понижается. При Ω = 0,008 условия развития
процесса мало отличаются от таковых при адиабатных условиях (Ω = 0). При
Ω > 0,025 из-за интенсивного теплоотвода замедляется развитие процесса са-
мовоспламенения, и оно становится н
евозможным.
Наиболее благоприятными для процесса самовоспламенения являются
адиабатные условия при поддержании концентраций реагирующих веществ
постоянными μ = С =1 и Ω = 0 (рис. 8.1).
Варьирование коэффициента избытка воздуха показало следующее. При
0,1< α < 1 имеет место интенсификация процесса самовоспламенения пыле-
воздушной смеси, что связано с уменьшением реакционной поверхности,
приходящейся на единицу массы газовой среды. В результате - ускоряется
разогрев смеси, способствующей развитию химических реакций. При даль-
нейшем у
меньшении α происходит понижение температуры из-за наличия
большого избытка топлива, и это задерживает развитие химического реаги-
рования. В случаях α >1 уменьшается реакционная поверхность и увеличива-
ется избыток воздуха, не участвующего в реакционном процессе. Итогом
0,14
0,10
0,06
0,2 0,4 0,6 0,8 lg(
1
)
= 0.025
= 0.008
= 0,
= 0
= C=1
,C - var

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
90
этого является уменьшение тепловыделения, приходящегося на единицу мас-
сы газовой среды, что замедляет рост температуры, а следовательно, и разви-
тие химического превращения.
Следовательно, наиболее благоприятные условия для самовоспламене-
ния в одномерном потоке при прочих равных условиях реализуются для сме-
си с недостатком воздуха. В конкретном случае оптимальное значение α за-
висит от физико-химически
х свойств топлива, от степени его тепловой и ме-
ханической подготовки, от температурных условий и концентрации кислоро-
да в реагирующей смеси.
8.2. Математическое моделирование аэродинамики топочных камер
Современная топочная техника отличается большим разнообразием аэ-
родинамических схем: наряду с традиционной встречной компоновкой вих-
ревых или прямоточных горелок и тангенциальной компоновкой находят
применение вихревые топки для малогабаритных котлов, топки с низкотем-
пературным вихрем, топки с плоскофакельными горелками, циклонные топ-
ки, а также многогранные кольцевые топки [5]. Такое разнообразие конст-
руктивных схем объясняется тем, что аэродинамика я
вляется одним из фак-
торов, определяющих процессы горения и теплообмена в топочных устрой-
ствах. Поэтому при создании новых конструкций котельных агрегатов боль-
шое внимание уделяется изучению аэродинамики газовых потоков внутри
топочных камер. Решение этого вопроса с помощью физического моделиро-
вания связано как с материальными, так и принципиальными трудн
остями. В
настоящее время развитие методов вычислительной гидродинамики [51],
[52], а также прогресс в области электронно-вычислительных машин позво-
ляют осуществлять математическое моделирование аэродинамических про-
цессов в топочных камерах. Такое направление очень перспективно, по-
скольку удачная математическая модель может позволить оперативно изме-
нять граничные условия, конфигурацию конструкции, а в дальнейшем – рас-
сматривать сов
местно с аэродинамическими и процессы тепломассообмена, а
также горения в котельных агрегатах.
Однако данный подход встречает на своем пути большие трудности, по-
скольку течения в топочных камерах носят пространственный характер, а по-
этому решаемые задачи сугубо трехмерны, и лишь в некоторых случаях за-
дачу можно свести к двухмерной системе уравнений. В св
язи с этим требует-
ся использование трехмерных сеток, учитывающих их реальную геометрию.
Реализация численных алгоритмов возможна с применением ЭВМ, обла-
дающих быстродействием и большим объемом памяти.
Физическая постановка задачи. Поскольку максимальные скорости газов
в топочных камерах не превышают 100 м/с, а температуры находятся вблизи
1800 К, то этим параметрам отвечают числа Маха M ≅ 0,12, а след
овательно
продукты сгорания можно считать несжимаемыми [5], [26]. При факельном
