Голдаев С.В., Ляликов Б.А. Основы математического моделирования в теплотехнике
Подождите немного. Документ загружается.


Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
31
Для определенности считаем, что F(a)<0, F(b)>0. Процесс итераций за-
ключается в том, что в качестве приближений к корню уравнения (3.1) при-
нимаются значения c
0
, c
1
точек пересечения ее с осью абсцисс
(
)
(
)
() ()
.
0
aFbF
aFab
ac
−
−
−=
(3.6)
Далее, сравнивая знаки величин F(b) и F(c
0
), приходим к выводу, что ко-
рень находится в интервале [c
0
, b]. Отрезок [a, c
0
] отбрасываем. Следующая
итерация состоит в определении нового приближения c
1
точки пересечения
хорды AB
1
с осью абсцисс и т.д. Процесс уточнения продолжается до тех
пор, пока значение F(c) не станет по модулю меньше заданного числа ε.
В методе деления отрезка пополам (его еще называют методом бисекции,
или дихотомии), также как и в предыдущем алгоритме, необходимо знать от-
резок [a, b], в котором расположено искомое значение корня x = c, т.е. a < c <
b. В качестве начального приближения корня c
0 принимается середина этого
отрезка, т.е. c
0
= (a+b)/2. Затем исследуется значение функции F(x) на концах
отрезков [a, c
0
] и [c
0
, b], т.е. в точках a, c
0
, b. Тот из них, на концах которого
F(x) принимает значения разных знаков, содержит искомый корень; поэтому
его принимают в качестве этого отрезка. Вторая половина отрезка [a, b], на
которой знак не меняется, отбрасывается. В качестве первой итерации корня
принимается середина нового отрезка и т.д. Таким образом, после каждой
итерации отрезок, на котором расположен ко
рень, уменьшается вдвое, т.е.
после n итераций он сокращается в 2n раз.
Предположим, что F(a) < 0, F(b) >0 (рис.3.2). В качестве начального при-
ближения корня принимается c
0
= (a+b)/2. Поскольку в рассматриваемом
случае F(с
0
) < 0, то с
0
< c < b, и рассматривается только отрезок [c
0
, b]. Сле-
дующее приближение: c
1
= (c
0
+b)/2. При этом отрезок [c
1
, b] отбрасывается,
поскольку F(с
1
) >0 и F(b) >0, т.е. с
0
< c < с
1
. Аналогично находятся другие
приближения: c
2
= (c
0
+с
1
)/2 и т.д.
Итерационный процесс продолжается до тех пор, пока значение функции
F(x) не станет меньшим по модулю некоторого заданного малого числа.
Как видно, алгоритмы метода хорд и метода деления отрезка пополам
похожи, однако первый из них в ряде случаев дает более быструю сходи-
мость итерационного процесса. Оба метода очень надежны при нахождении
корня, если отрезок смены знаков функции указан верно.
В тех случаях, когда функция y = f(x, p
1
,p
2
,…) достаточно проста, исполь-
зуют алгоритм касательных (метод Ньютона) [18], [20-23], [32], [36], в соот-
ветствии с которым последующая и предыдущая итерации связаны таким об-
разом:
(
)
(
)
./
1 iiii
mFmFmm
′
−=
+
(3.7)
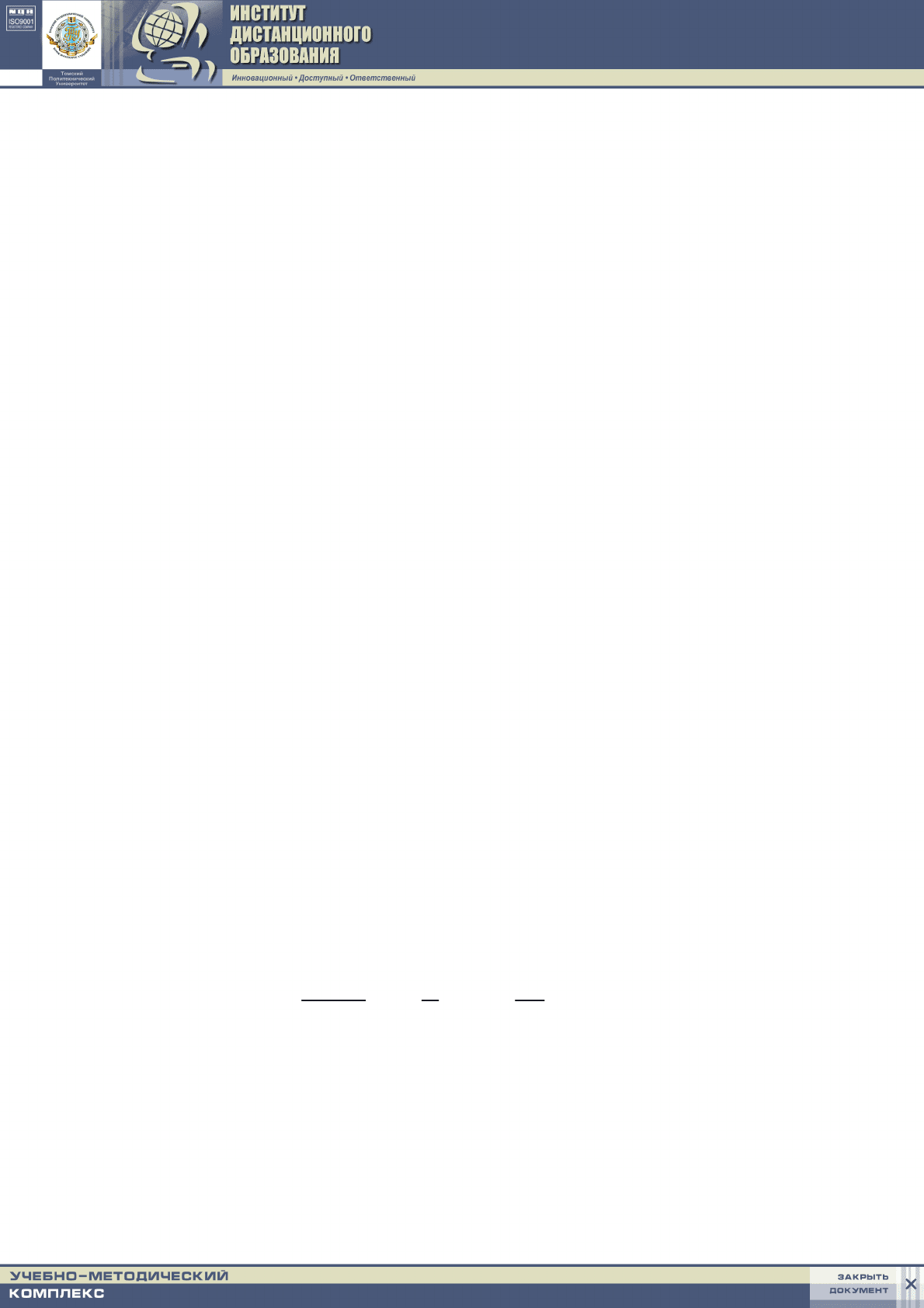
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
32
Процесс может считаться законченным, если будет удовлетворяться ус-
ловие (3.4). Данный метод из всех итерационных процессов имеет самую вы-
сокую скорость сходимости.
Рассмотрим несколько задач, при решении которых будут использоваться
описанные выше алгоритмы.
Пример 3.1. В ходе изучения процессов теплового излучения абсолютно
черного тела рассматриваются два предельных случая, вытекающих из зако-
на Планка. При выводе закона смещения Вина рассматривается следующее
трансцендентное уравнение относительно безразмерной температуры [27],
[28], [30]:
(
)
[]
,/,exp15
2
TCuuu
v
λ
=
−
−=
где T – абсолютная температура, К; C
2
– вторая константа излучения,
м⋅К;
λv – длина волны, м.
Согласно итерационному методу (3.3), записываем:
(
)
[]
.exp15
1 ii
uu
−
−
=
+
Структура уравнения очень проста, и его решение легко получить “вруч-
ную”. В методических целях воспользуемся программой расчета, которая
представлена выше.
Поскольку исходное уравнение получено в предположении u >> 1, то в
качестве нулевого приближения полагаем u
0
=3. Задаем точность, равную
0,005, а количество возможных циклов –10. Последующие итерации прини-
мают такие значения: u
1
= 4,751, u
2
= 4,957, u
3
= u
4
= 4,965. Процесс быстро
заканчивается, что обусловлено как видом уравнения, так и выбором началь-
ного приближения.
Пример 3.2 Расчет конвективного нагрева (охлаждения) пластины толщи-
ной 2δ осуществляется с использованием решения соответствующей краевой
задачи, имеющего вид [28]:
()
()
∑
∞
=
−=Θ
1
2
,expcos
k
kkk
FomzmA
(3.8)
где
2
,,
δ
τ
δ
a
Fo
x
z
tt
tt
lH
l
==
−
−
=Θ
(3.9)
- безразмерные: температура, координата и время (критерий Фурье);
a – коэффициент температуропроводности; t
H
, t
l
- температуры (начальная
пластины и окружающей среды).
Коэффициент A
k
вычисляется по формуле:

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
33
(
)
() ()
kkk
k
k
mmm
m
A
cossin
sin2
+
=
.
(3.10)
Входящие в (3.8) и (3.10) параметры m
k
являются корнями трансцен-
дентного уравнения
()
,/ Bimmctg
kk
=
(3.11)
где
λ
αδ
/
=
Bi
(3.12)
- критерий Био, λ - коэффициент теплопроводности.
При Fo > 0,3 в инженерных расчетах используют первый член ряда. Тогда
(3.8) имеет вид:
()
(
)
.expcos
2
111
FomzmA −=Θ
(3.13)
Средняя температура пластины вычисляется по формуле
(
)
[]
22
1
2
1
2
1
2
exp2
BiBimm
FomBi
tt
tt
lH
l
++
−
=
−
−
=Θ
.
(3.14)
Теплота, отданная телом за время τ в процессе охлаждения или воспри-
нятая за этот промежуток времени в процессе нагрева, рассчитывается по
формуле:
(
)
(
)
,,1
lHPP
ttVcQQQ
−
=
Θ−=
ρ
(3.15)
где Q
P
– полная теплота, выделяемая (или воспринятая) за время перехода
тела в термическое равновесие с окружающей средой.
Значения m
k
при различных критериях Bi имеются в таблицах [28], [30],
однако такой способ неудобен при проведении расчетов на ЭВМ по выпи-
санным формулам. Гораздо проще иметь подпрограмму численного решения
трансцендентного уравнения (3.11).
Воспользуемся методом хорд. В соответствии с формулой (3.6), имеем:
()
(
)
() ()
,
ab
aab
ac
mFmF
mFmm
mm
−
−
−=
(3.16)
где
()
(
)
./ mctgBimmF
−
=
Согласно справочным данным [28], [30], при 0 < Bi < ∞ значения корня
m
1
находятся в пределах от 0 до 1,6, в частности, при Bi = 0,5 табличное зна-
чение 6533,0
)(
1
=
t
m . Поэтому в качестве интервала выбираем: m
a
= 0,4, m
b
=
1,2. Функция в этих точках принимает следующие значения: F(m
a
) = 1,565,
F(m
b
) = -2,011, а первое приближение, согласно (3.16), – m
c1
= 0,75. На сле-
дующей итерации положение левой границы оставляем прежним, а правую
переносим в точку m
c0
. В результате такой процедуры получаем m
c2
= 0,675, и
функция в ней остается отрицательной. Продолжая в соответствии с данным

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
34
алгоритмом, имеем: m
c3
= 0,6584, m
c4
= 0,6544, m
c5
= 0,6536. Последнее при-
ближение отличается от табличного значенния на 0,14%.
Пример 3.3. По стальному трубопроводу (коэффициент теплопроводно-
сти λ
1
= 50 Вт/м⋅
0
С), покрытому двумя слоями тепловой изоляции одинако-
вой толщины δ, перекачивается горячий жидкий теплоноситель, имеющий
температуру t
l,1
= 502,5
0
C. Снаружи находится спокойный воздух, темпера-
тура которого t
l,2
= 15
0
C. Температура стенки трубопровода, омываемой
жидкостью, t
1
= 500,1
0
C, температура второго слоя изоляции, контактирую-
щего с воздухом t
4
= 60
0
C , коэффициент теплоотдачи от него в окружаю-
щую среду α
2
= 10 Вт/(м
2 0
С). Внутренний диаметр трубы d
1
= 0,103 м, на-
ружный d
2
= 0,109 м, коэффициенты теплопроводности слоев изоляции: λ
2
=
0,204 Вт/(м ⋅
0
С), λ
3
= 0,0904 Вт/(м.
0
С).
Требуется найти температуры контакта слоев изоляции t
2
, t
3
, их толщину,
тепловой поток через образующую цилиндра Q Вт/м.
Решение. Используя равенство тепловых потоков через любое сечение
многослойной системы, а также исходные данные, запишем [28]:
()
(
)
,4
2,422 l
ttdQ
−
+
=
δ
πα
()
.
2
4
ln
1
2
ln
1
ln
1
2
2
2
32
2
21
2
1
41
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
δ
δ
λ
δ
λλ
π
d
d
d
d
d
d
tt
Q
(3.17)
Исключая Q, приходим к следующему трансцендентному уравнению от-
носительно толщины стенки изоляции:
()()
(
)
(
)
[]
,021ln1ln121
2
=
−
+
+
+
−
+
+ AxkxkExBi
λλ
(3.18)
в котором для удобства анализа использованы безразмерные переменные и
параметры:
2,4
41
2
22
2
1
2
1
2
3
2
2
,
2
,ln,,
2
l
tt
tt
A
d
Bi
d
d
Ek
d
x
−
−
==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
===
λ
α
λ
λ
λ
λδ
λ
.
(3.19)
Их числовые значения в рассматриваемом примере следующие: k
λ
=
2,2566, E = 2,31⋅10-4, Bi
2
= 2,672, A = 9,78.
Для решения (3.18) применим метод дихотомии. Принимаем из интуи-
тивных соображений a = 0,5, b = 1,5. Проверяем знаки функций на концах
выбранного отрезка и убеждаемся, что F(a) = -4,14, F(b) = 11,35. В средине
отрезка с
0
=(a+b)/2 = 1, F(c
0
) = 3, 3125. Затем делим отрезок [a, c
0
] пополам с
1
=(a+c
0
)/2 = 0,75, F(c
1
) = -6, 637 и видим, что корень уравнения находится
внутри отрезка [c
1
, c
0
]. Продолжая процедуру уточнения, таким же путем на-

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
35
ходим, что отличие восьмого приближения от седьмого не превышает 0,5%.
Поэтому в качестве искомого решения можно взять значение x = с
8
= 0,8.
Следовательно, толщина и диаметры слоев изоляции равны соответственно
2
2
1036,42/
−
⋅== xd
δ
м,
196,02
23
=
+=
δ
dd
м,
283,02
34
=
+
=
δ
dd
м.
Тогда
()
(
)
65,40042
2,422
=
−
+=
l
ttdQ
δ
πα
Вт/м .
Для проверки правильности найденного решения вычисляем
C
d
Q
tt
l
0
42
2,4
06,60=+=
πα
.
Величина коэффициента теплоотдачи и температуры контакта слоев рав-
ны:
()
53,509
11,1
1
=
−
=
ttd
Q
l
π
α
Вт/(м
2
С),
,500ln
2
0
1
2
1
12
C
d
dQ
tt =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
πλ
.2,385ln
2
0
3
4
2
23
C
d
d
Q
tt =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
πλ
Пример 3.4. В балло находится двуокись углерода под давлением. pr =
3,923 МПа и при температуре T
r
= 293,2 К. Вычислить удельный объем по
уравнениям : 1) Клапейрона и 2) Ван-дер-Ваальса.
Решение. По уравнению состояния идеального газа получаем:
0141,0
10923,3
29391,188
6
,
=
⋅
⋅
==
r
r
ir
p
RT
v
м
3
/кг,
(3.20)
где R – удельная газовая постоянная, Дж/(кг⋅К).
Уравнение состояния Ван-дер-Ваальса, являющееся наиболее теоретиче-
ски обоснованным, имеет вид [33]
(
)
(
)
rrrr
RTbvvap =−+
2
/
,
(3.21)
где a = 190,9 Н⋅м
4
/кг
2
, b = 9,84⋅10
-4
м
3
/кг – постоянные для данного газа.
Удобнее расчет проводить по уравнению состояния в приведенной форме:
()
(
)
,03983,,
23
0
=−++−= vvppvpvF
θθ
(3.22)
где
./,/,/
krkrkr
TTvvvppp
=
==
θ
(3.23)
Здесь нижним индексом обозначены соответствующие термодинамиче-
ские параметры в критическом состоянии. В частности для двуокиси углеро-
да они равны: p
k
= 7,38 МПа, v
k
= 0, 0021, T
k
= 304,2. Тогда p = 0,5316, θ =
0,9637.
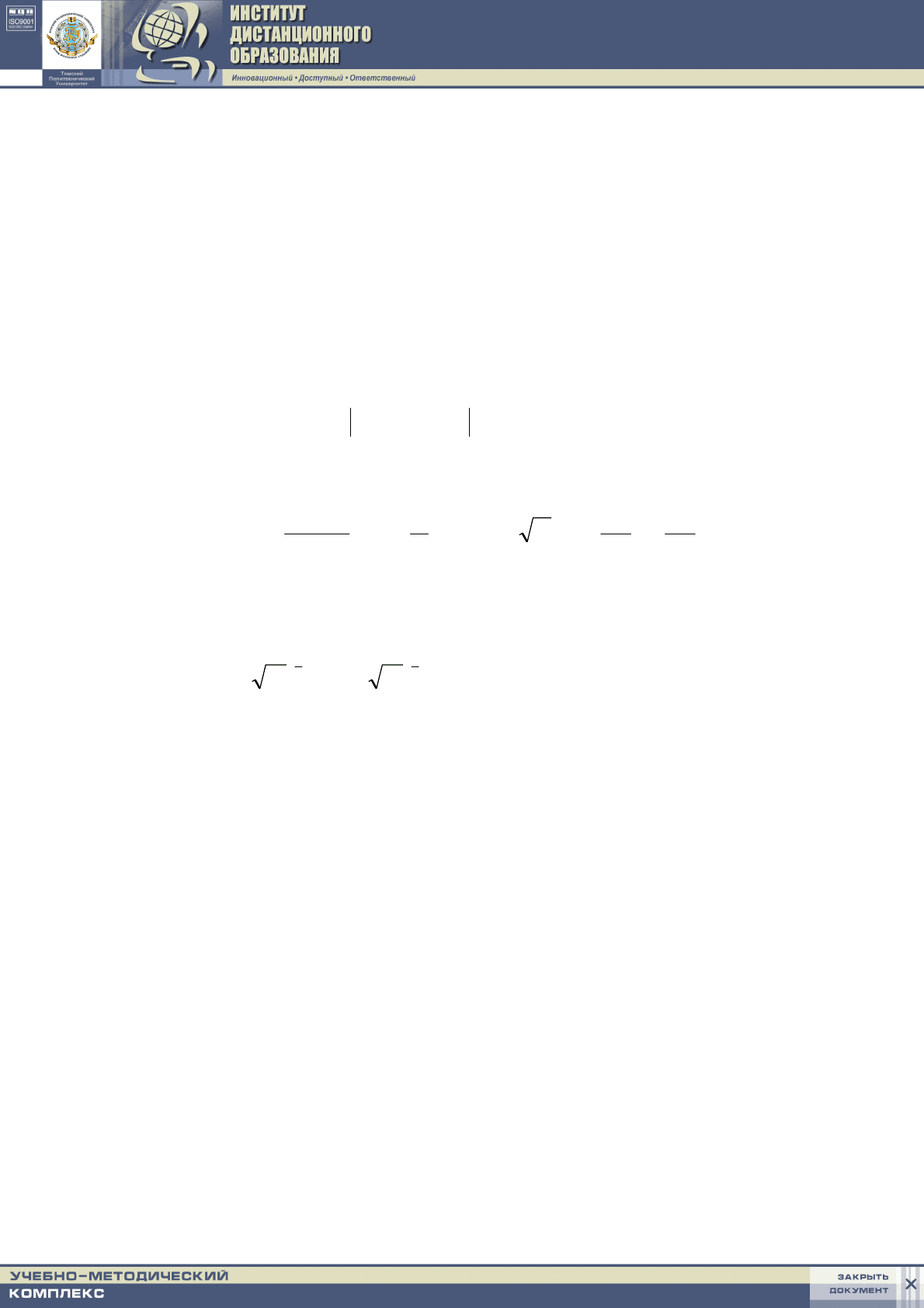
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
36
Численное решение уравнения (3.22) получим методом касательных.
Дифференцируя его по ν, получаем:
()
(
)
9829/,,
2
1
++−== vppvdvdFpvF
θθ
.
(3.24)
Подставляя в формулу (3.7), имеем рекуррентное выражение для уточне-
ния решения уравнения (3.22):
()
(
)
.,,/,,
101
θ
θ
pvFpvFvv
iiii
−
=
+
(3.25)
В качестве нулевого приближения ν
0
принимаем значение приведенного
объема, вычисленного по уравнению Клапейрона и равного ν
id
= ν
r,i
/ν
k
=
6,6064. Уточняя по формуле (3.25), получаем: ν
1
= 5,1686, , ν
2
= 4,3248, ν
3
=
3,9284, v
4
= 3,8188. Процесс закончен, т.к. на этой итерации удовлетворяется
неравенство
()
002,0/
445
<− vvv
.
Для проверки достоверности полученного результата было найдено точ-
ное значение ν
t
по формуле Кардано [36]. Определяя знак дискриминанта
,
2
1
2
3
,
1
9
8
,
2
23
pp
wwsw
p
r
p
p
wsrD −
⎥
⎦
⎤
⎢
⎣
⎡
−=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=+=
θ
(3.26)
убеждаемся, что в рассматриваемом примере r = -1,086, s = -1,191, D = 0,138.
Поскольку D >0 , то уравнение (3.22) имеет единственное вещественное ре-
шение, которое вычисляется так:
()()
()
.8188,3)9/(8
3
1
3
1
0
=+++−+−= ppDsDsv
θ
(3.27)
Сравнение величины приведенного объема, найденного по методу Нью-
тона, с точным значением показывает, что они практически совпадают.
4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
Численное дифференцирование применяется в тех случаях, когда функ-
цию y(x) трудно или невозможно продифференцировать аналитически, на-
пример, когда она задана таблично. Гораздо чаще оно используется при ре-
шении дифференциальных уравнений разностными методами, что будет по-
казано ниже.
Как известно, производной функции y = f(x) называется предел отноше-
ния приращения функции Δy к приращению аргумента Δx при стремлении
его к нулю [36
]. Аппроксимацией производной с помощью отношения ко-
нечных разностей является приближенное равенство [18], [20]:
xyy
Δ
Δ
≅
′
/
.
(4.1)
В зависимости от способа вычисления конечных разностей получаются
различные формулы для вычисления производной в одной и той же точке:
с помощью левых, правых и центральных разностей:
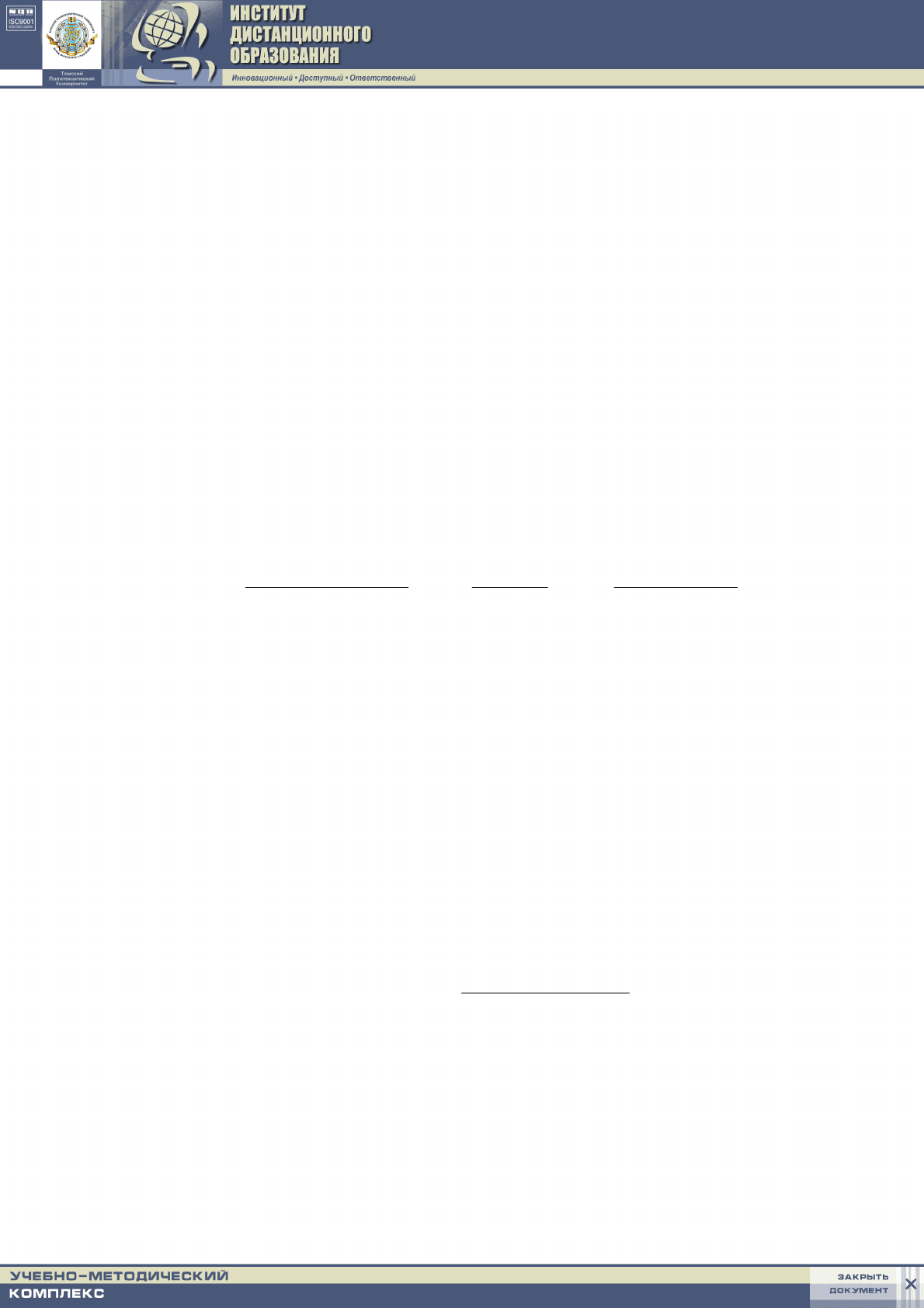
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
37
(
)
,/
011
hyyy
−
≅
′
−
(4.2)
(
)
,/
121
hyyy
−
≅
′
(
4.3)
(
)
.2/
021
hyyy
−
≅
′
(4.4)
Погрешности, возникающие при численном дифференцировании, опре-
деляются погрешностями аппроксимации. Например, формулы (4.2), (4.3)
имеют первый порядок, а формула (4.4) – второй порядок. Кроме этого, ока-
зывают влияние неточные значения функции y
i
в узлах и ошибки округления
при проведении расчетов на ЭВМ. В отличие от погрешности аппроксима-
ции, ошибка округления возрастает с уменьшением шага h. Поэтому суммар-
ная погрешность численного дифференцирования может убывать при
уменьшении шага лишь до некоторого предельного значения, после чего
дальнейшее уменьшение шага не повысит точности результатов.
Оптимальная точность достигается за счет регуляризации проц
едуры
численного дифференцирования, которая осуществляется на практике путем
сглаживания табличных значений величин подбором некоторой аппроксими-
рующей функции, например, многочлена Лагранжа. В частности выражения
для первой производной для трех узлов (n = 2) интерполяции имеют вид:
h
y
yy
y
h
yy
y
h
yyy
y
2
34
,
2
,
2
43
10
2
02
1
210
0
+
−
=
′
−
=
′
−+−
=
′
(4.5)
При четных n выражения для производных в средних узлах c произволь-
ным номером i имеют наиболее простой вид и широко используются на
практике:
(
)
;2/:2
11
hyyyn
iii −+
−
=
′
=
(4.6)
(
)
[]
.12/8:4
2112
hyyyyyn
iiiii +−+−
−
−
+
=
′
=
(4.7)
Порядок точности конечно-разностных соотношений для аппроксимаций
производных прямо пропорционален числу используемых узлов, они стано-
вятся более громоздкими, что приводит к существенному возрастанию объе-
ма вычислений. Известен простой и эффективный способ уточнения решения
при фиксированном числе узлов, используемых в аппроксимирующих ко-
нечно-разностных соотношениях, предложенный Рунге. Вычисляя производ-
ную с порядком точности p вна
чале при шаге h, а затем при h
1
= k
h
, получают
ее значение по формуле:
() ()
(
)
(
)
.
1
,,
,,
~
−
′
−
′
+
′
=
′
p
h
khxyhxy
hxyhxy
(4.8)
Таким приемом порядок точности можно повысить на единицу.
Проиллюстрируем отмеченные выше аспекты численного дифференци-
рования на следующих задачах из области технической термодинамики, где
подобную операцию приходится применять при решении задач с фазовыми
переходами [33], [38], [40].
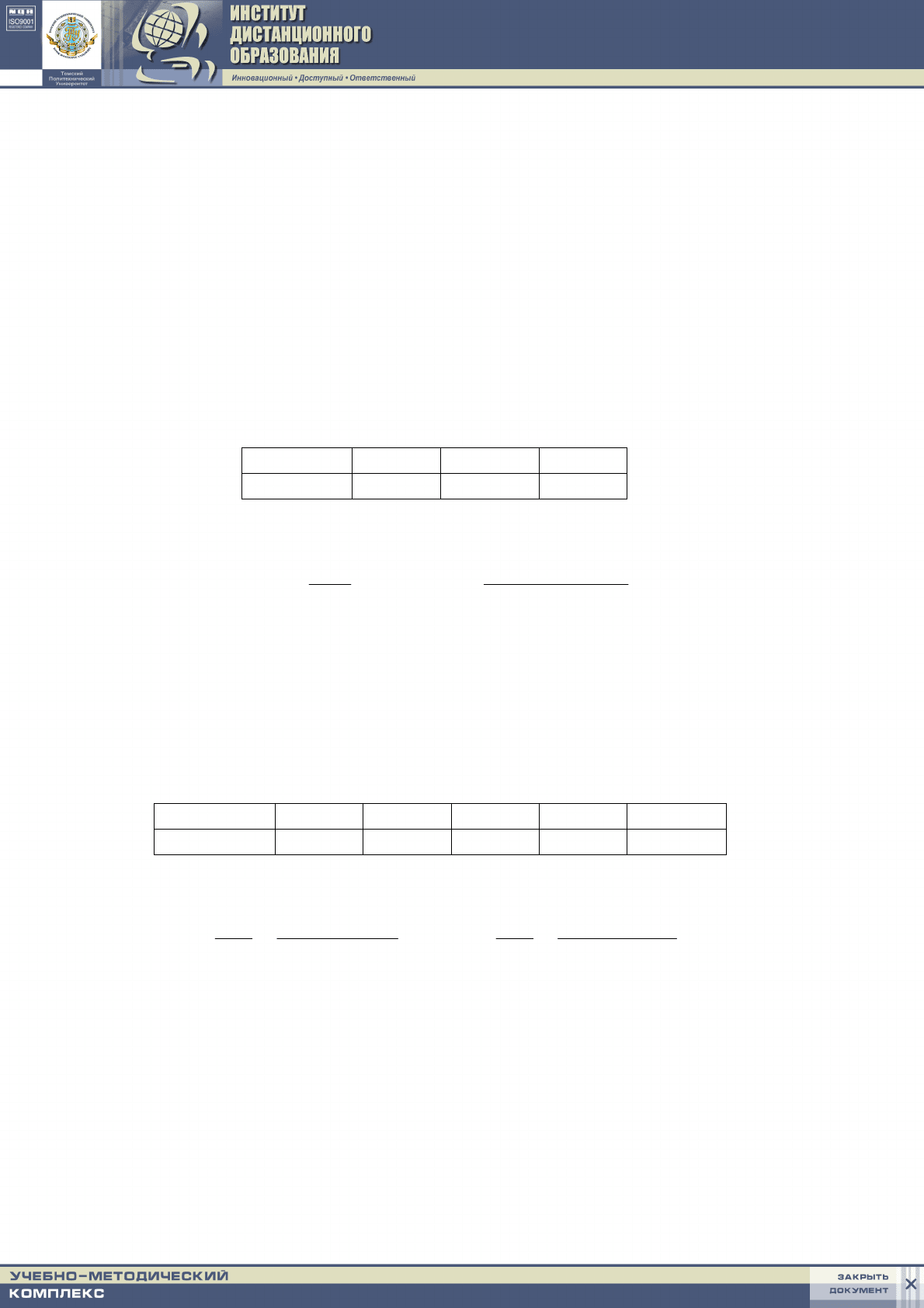
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
38
Пример 4.1. Теплота парообразования бензола C
6
H
6
при Т
1
= 323 К рав-
на r
1
= 416 кДж/кг, а при Т
2
= 353 К она равна r
2
= 398, 6 кДж/кг. Определить
теплоемкость парообразного бензола
''
p
c в пределах этих температур, если
теплоемкость жидкого бензола:
73.1
'
=
p
c
кДж/(кг⋅К).
Используя уравнение Кирхгофа в конечных разностях [33], получим:
15.1)353323/()6.398416(73.1/
'''
=−−+=ΔΔ+= Trcc
pp
кДж/(кг⋅К).
Пример 4.2. Ввиду неустойчивости состояния системы на пограничной
линии для определения объема сухого насыщенного пара (v′′) используется
уравнение Клапейрона – Клазиуса [34]. Нужно определить v′′ при p = 0,491
МПа, если из опыта известно, что теплота парообразования r = 2120 кДж/кг,
v′= 0,00109 м
3
/кг, а зависимость T = f(p) представлена такими данными:
p, МПа 0,443 0,491 0,541
Т , К 420,1 424 427,6
Из уравнения Клапейрона – Клазиуса, записанного в конечных разностях,
имеем:
кгм
pT
Tr
vv /3821,0
10098,0424
5,71012,2
1009,1
3
6
6
3
=
⋅⋅
⋅⋅
+⋅=
Δ
Δ
+
′
=
′′
−
.
Для сравнения укажем табличное значение:
./3818,0
3
кгмv =
′′
Пример 4.3. При помощи уравнения Клапейрона - Клазиуса требуется оп-
ределить теплоту парообразования r водяного пара при t = 210
0
C и сравнить
ее с табличным значением r
T
= 1900 кДж/кг. Производную dp
s
/dT
s
рекомен-
дуется найти приближенно методом конечных разностей на основании сле-
дующей зависимости давления насыщения от температуры насыщения:
t
s
,
0
C 208 209 210 211 212
p
s
, МПа 1,833 1,871 1,909 1,947 1,987
Ограничимся в этой задаче только стадией нахождения производной. Ис-
пользуя формулы (4.3) и (4.4), получаем:
.038,0
2
871,1947,1
,038,0
1
909,1947,1
≅
−
≅≅
−
≅
s
s
s
s
dT
dp
dT
dp
Несмотря на то, что примененные формулы имеют различный порядок
точности, погрешность вычисления dp
s
/dT
s
оказалась одинаковой. Подобный
результат может быть объяснен достаточно малым шагом по температуре и
не очень сильным изменением давления на этом интервале.
Пример. 4.4. Требуется определить объем кипящей ртути при полном пе-
реходе ее в насыщенный пар для t = 250
0
C, если известны величина объема
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
39
v′, теплота фазового перехода r = 298,452 кДж/кг и зависимость p
s
= p(T
s
) ,
заданная таблично:
t
s
,
0
C 230 240 250 260 270
p
s
, кПа 5,758
7,614 9,959 12,892 16,527
Используя уравнение Клапейрона – Клазиуса, выразим из него искомый
объем насыщенного пара ртути:
()
sss
dTdpT
r
vv
/
+
′
=
′′
.
Вычисляя производную по формуле (4.3), имеющую первый порядок
точности, получаем в итоге: v′′ =1,922 м
3
. Сравнивая с табличным значением
объема, равным v′′ =2,176 м
3
, видим, что ошибка составляет 11,7%.
Применение аппроксимационной зависимости (4.4) позволяет уменьшить
погрешность расчета производной, а соответственно и объема, почти на по-
рядок: v′′ =2.14 м
3
(ошибка 1,7%). Дальнейшее уточнение вычислений дос-
тигнуто путем использования формулы численного дифференцирования для
пяти узлов (4.7); в результате получено:
''
T
v =2,155 м
3
(ошибка 1%).
Пример.4.5 При помощи уравнения Клапейрона- Клазиуса, опреде-
лить теплоту парообразования r водяного пара при t = 85
0
C и сравнить ее с
табличным значением r
T
= 2295 кДж/кг. Производную dp/dT найти прибли-
женными методами конечных разностей на основании следующей зависимо-
сти давления насыщения от температуры насыщения:
t
s
,
0
C 75 80 85 90 95
p
s
⋅10
-5
, Па
0,3855 0,9736 0,5781 0,7011 1,0132
Пренебрегая величиной объема жидкости и используя уравнение состоя-
ния идеального газа для нахождения значения объема пара (ошибка для тако-
го малого давления составляет примерно 0,7 %), запишем:
s
s
s
su
dT
dp
p
TR
r
μ
2
=
,
где R
u
= 8314 Дж/кмоль – универсальная газовая постоянная, μ = 18,016
кг/кмоль – молекулярная масса водяного пара.
Принимая температуру t = 85
0
C в качестве центральной точки, с исполь-
зованием формулы (4.3), имеем:
()
3
5
1046,2
5
105781,07011,0
⋅=
⋅−
=
s
s
dT
dp
Па/К.
Вычисляя теплоту парообразования и сравнивая это значение с таблич-
ным, получаем:
(
)
2519
105781,0016,18
1046,215,3588314
5
3
2
=
⋅⋅
⋅⋅
=r
кДж/кг ;
.107,9
2−
⋅=
−
T
T
r
rr

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
40
Полагая в формуле Рунге p = 1, т.к. (4.3) имеет первый порядок аппрок-
симации, и k = 2 – двукратное увеличение шага по температуре, получаем
уточненное значение производной:
.1025,210]
1)2(
67,246,2
46,2[
~
,1067,2
10
10)5781,08451,0(
33
1
3
5
⋅=⋅
−
−
+=
⋅=
⋅−
=
′
s
s
s
s
dT
pd
dT
pd
Этой величине производной соответствует теплота парообразования
r=2304 кДж/кг, которая отличается от табличного значения на 0,5%.
5. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
5.1. Приближенное интегрирование
К вычислению определенного интеграла сводится ряд задач в области те-
плотехники. Например, нахождение термодинамических функций (энталь-
пии, энтропии, внутренней энергии), усредненных значений температур, ко-
личеств поглощенной или отданной теплоты [28-30], [33], [38], [40].
В курсе высшей математики [36] показано, что определенный интеграл, в
соответствии с формулой Ньютона – Лейбница, равен приращению первооб-
разной F(x) на заданном отрезке интегрировани
я:
() () () ()
∫
−==
b
a
b
a
aFbFxFdxxf .
(5.1)
Пример 5.1 Определить значение энтальпии воздуха, отсчитанное от 0
0
С, при температуре t
1
= 287,0
0
С, если задана интерполяционная формула для
удельной теплоемкости воздуха
,
2
210
tataac
p
++=
где a
0
= 0,9972, a
1
= 2,139⋅10-4 , a
2
= -2,905⋅10-8 .
Как известно из технической термодинамики [33], dh/dt = c
p
. Принимая
во внимание, что при t = 0
0
C энтальпия h
0
= 0, можно записать:
∫
=
t
pt
dtch
0
.
Используя аппроксимационную зависимость для теплоемкости, и выпол-
няя интегрирование, получаем следующее выражение:
3/2/
3
3
2
10
tatatah
t
++=
.
Подставляя числовые значения коэффициентов и температуры, находим
требуемое значение энтальпии h
287
= 294, 78 кДж/кг.
Однако на практике таким приемом не удается воспользоваться по не-
скольким причинам: 1) вид функции f(x) не допускает непосредственного ин-
