Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

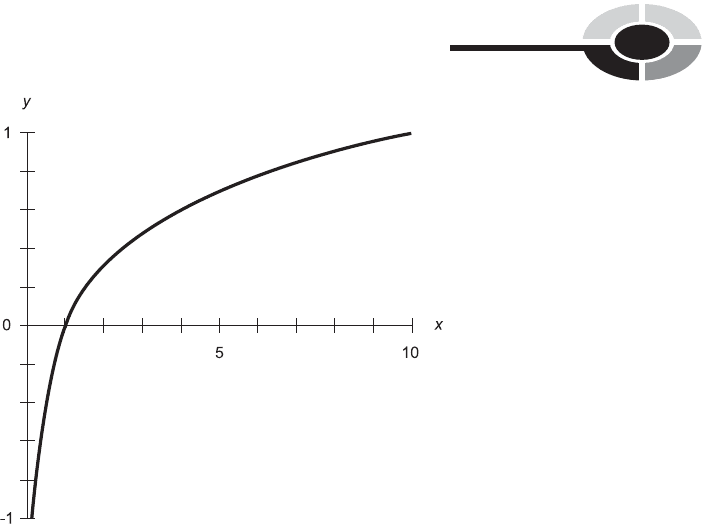
Figure 14-6 is an approximate graph of the function y ¼ log x. The domain

is limited to the positive real numbers. The range encompasses the entire

set of real numbers.

NATURAL LOGARITHMS

Base-e logarithms are also called natural logs or Napierian logs.In

equations, the natural-log function is usually denoted ‘‘ln’’ or ‘‘log

.’’ For

example:

ln 2:71828 ¼ log

2:71828  1:00000

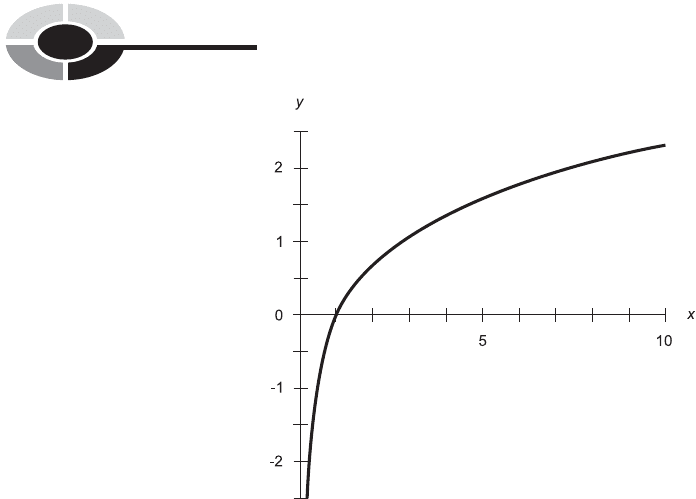
Figure 14-7 is an approximate graph of the function y ¼ ln x. The domain

is limited to the positive real numbers, just as in the case of the common

log function. The range of the natural log function, also like the common

log function, encompasses the entire set of real numbers.

HOW DO WE FIND THEM?

Common and natural logarithms can be easily and quickly found using a

scientiﬁc calculator. That’s all you have to know for practical purposes.

Fig. 14-6. Approximate graph of the common logarithm function.

CHAPTER 14 Growth and Decay 351

Once you have learned which keys to use (the instructions can help you with

this if it isn’t obvious), ﬁnding logarithms is painless.

Rules for Logarithms

Logarithmic functions, like their exponential-function counterparts, make it

possible to work with numbers in unique ways. And, as with exponentials,

logarithms have a way of coming up in work nowadays. Here are some

rules you should know about logarithmic functions.

LOGARITHM OF PRODUCT

If x and y are both positive real numbers, the common logarithm of the

product is equal to the sum of the common logarithms of the individual

numbers:

log xy ¼ log x þ log y

The natural logarithm of the product is equal to the sum of the natural

logarithms of the individual numbers:

ln xy ¼ ln x þ ln y

Fig. 14-7. Approximate graph of the natural logarithm function.

PART 4 Math in Science

352

LOGARITHM OF RATIO

Let x and y be positive real numbers. The common logarithm of their ratio,

or quotient, is equal to the diﬀerence between the common logarithms of

the individual numbers:

logðx=yÞ¼log x  log y

The natural logarithm of their ratio, or quotient, is equal to the diﬀerence

between the natural logarithms of the individual numbers:

lnðx=yÞ¼ln x  ln y

LOGARITHM OF QUANTITY RAISED TO A POWER

Let y be a real number, and let x be a positive real number. The common

logarithm of x raised to the power y can be expressed as a product:

log x

¼ y log x

The natural logarithm of x raised to the power y can be expressed as a

product:

ln x

¼ y ln x

LOGARITHM OF RECIPROCAL

Let x be a positive real number. The common logarithm of the reciprocal of x

is equal to the negative of the common logarithm of x, as follows:

logð1=xÞ¼log x

The natural logarithm of the reciprocal of x is equal to the negative of the

natural logarithm of x, as follows:

lnð1=xÞ¼ln x

LOGARITHM OF THE ROOT OF A QUANTITY

Let x be a positive real number. Let y be any real number except 0. The

common logarithm of the yth root of x (also denoted as x to the 1/y

power) is given by:

log x

ð1=yÞ

¼ðlog xÞ=y

CHAPTER 14 Growth and Decay 353

The natural logarithm of the yth root of x (also denoted as x to the 1/yth

power) is given by:

ln x

ð1=yÞ

¼ðln xÞ=y

PERCEIVED INTENSITY

If you have ever done serious work with high-ﬁdelity (hi-ﬁ) equipment,

you’ve heard about units called decibels, symbolized dB. The decibel is a

logarithmic unit. It is used to express the relative intensity of sound waves,

radio signals, and even visible light.

The concept of the decibel evolved because our senses perceive variable

eﬀects according to the logarithm of the intensity, not in direct proportion to

the intensity. This is a defense mechanism against the harshness of the world.

If we perceived phenomena such as sound and light in direct proportion

to their true levels, the variability would be overwhelming. We might not be

able to hear someone whispering a meter away, yet a trumpet blast from

across a room would knock us out. We might not be able to see the full moon

on a clear night, but we would be blinded by the light of a cloudy day.

Imagine two sounds having the same frequency and wave shape, such as

middle C played on a trombone. Call them ‘‘sound number 1’’ and ‘‘sound

number 2.’’ Imagine that a trombone plays note 1, pauses for a moment, and

then plays note 2. Notes 1 and 2 diﬀer in intensity by 1 dB if the change is just

barely enough so that a listener can tell the diﬀerence when the change is

expected. This turns out to be a diﬀerence in audio power of approximately

26%, or a ratio of 1.26:1. If the change is not expected, the smallest

detectable audio power diﬀerence is about 100%, or a ratio of 2:1 (believe it

or not).

If P

is the power (in watts) contained in sound 1 and P

is the power

(also in watts) contained in sound 2, their relationship in decibels, R, is given

by this formula:

R ¼ 10 logðP

This formula also works for radio-signal power and light-brilliance power.

If we know the relationship R in decibels between phenomenon number 1

and phenomenon number 2, then the actual power ratio P

is a common

exponential function of R, as follows:

¼ 10

ðR=10Þ

PART 4 Math in Science

354

PROBLEM 14-11

Suppose two sounds diﬀer in volume by a power ratio of 2:1, which allegedly

is the smallest diﬀerence a listener can detect if the change is not anticipated.

What is the ratio in decibels?

SOLUTION 14-11

Use the formula above. Let P

¼ 2 and P

¼ 1. Then:

R ¼ 10 logðP

¼ 10 logð2=1Þ

¼ 10 log 2

¼ 10  0:30103

¼ 3:0103 dB

We can round this oﬀ to 3 dB.

PROBLEM 14-12

Suppose you are listening to a musical recording and the needles on your hi-ﬁ

ampliﬁer are peaking at a reading of 0 dB. You boost the volume until the

needles kick up to þ10 dB. By what factor have you increased the audio

power level?

SOLUTION 14-12

In the formula, set R ¼ 10 because the change in sound volume is þ10 dB.

From this, calculate the audio power ratio:

¼ 10

ðR=10Þ

¼ 10

ð10=10Þ

¼ 10

This means you have increased the audio power by a factor of 10:1.

Graphs Based on Logarithms

Logarithms make it possible to graph certain functions that don’t lend them-

selves to clear portrayal on the rectangular (Cartesian) coordinate plane.

This is done by making the increments on one or both axes proportional

to the logarithm of the variable value, rather than directly proportional to

CHAPTER 14 Growth and Decay 355

the variable value. A scale or axis in which the sizes of the increments are

in direct proportion to the variable value is called a linear scale or a linear

axis. A scale or axis in which the sizes of the increments are in proportion

to the logarithm of the variable value is called a logarithmic scale or a

logarithmic axis.

SEMILOG (x-LINEAR) COORDINATES

Figure 14-8 shows semilogarithmic (semilog) coordinates for deﬁning points in

a portion of the xy-plane. The independent-variable (x) axis is linear, and the

dependent-variable ( y) axis is logarithmic. In this example, functions can be

plotted with domains and ranges as follows:

1  x  1

0:1  y  10

The y axis in Fig. 14-8 spans two orders of magnitude (powers of 10).

The span could be larger or smaller than this, but in any case the y values

cannot extend all the way down to 0. This is because the logarithm of 0 is

undeﬁned.

Fig. 14-8. Semilog xy-plane with linear x axis and logarithmic y axis.

PART 4 Math in Science

356

SEMILOG ( y-LINEAR) COORDINATES

Figure 14-9 shows a diﬀerent sort of semilog coordinate system for deﬁning

points in a portion of the xy-plane. Here, the independent-variable ( x) axis

is logarithmic, and the dependent-variable ( y) axis is linear. In this example,

functions can be plotted with domains and ranges as follows:

0:1  x  10

1  y  1

The x axis in Fig. 14-9 spans two orders of magnitude. The span could be

larger or smaller, but in any case the x values cannot extend all the way

down to 0.

LOG–LOG COORDINATES

Figure 14-10 shows log–log coordinates for deﬁning points in a portion of

the xy-plane. Both axes are logarithmic. In this example, functions can be

plotted with domains and ranges as follows:

0:1  x  10

0:1  y  10

Fig. 14-9. Semilog xy-plane with logarithmic x axis and linear y axis.

CHAPTER 14 Growth and Decay 357

Fig. 14-10. Log–log xy-plane. Both axes are logarithmic.

Fig. 14-11. Illustration for Problem 14-13.

PART 4 Math in Science

358

The axes in Fig. 14-10 span two orders of magnitude. The span of either axis

could be larger or smaller, but in any case the values cannot extend all the

way down to 0.

PROBLEM 14-13

In semilog coordinates, graph the world population p, in population units,

as a function of time t, in centuries, according to the theory of Professor P.

Show the function over the domain from t ¼ 0 (right now) to t ¼ 2(2

centuries, or 200 years, from now). Use a linear scale for the horizontal

axis and a logarithmic scale for the vertical axis.

SOLUTION 14-13

Refer to Fig. 14-11. Note that the graph is a straight line. One of the

major assets of semilogarithmic coordinates is the fact that they can

show exponential and logarithmic functions as straight lines, rather than as

curves.

Quiz

Refer to the text in this chapter if necessary. A good score is eight correct.

Answers are in the back of the book.

1. Imagine a frog that jumps halfway to a wall. After 10 seconds, it

jumps halfway to the wall again. After another 10 seconds, it jumps

halfway to the wall once again. It keeps repeating this process. In

theory, how long will it take to reach the wall after its ﬁrst jump?

(a) More information is needed to answer this question.

(b) 10

, or 100, seconds.

, or 1024, seconds.

(d) It will never reach the wall.

2. Imagine a frog that jumps halfway to a wall. After 4 seconds, it jumps

halfway to the wall again. After 2 seconds, it jumps halfway to the

wall again. After 1 second, it jumps halfway to the wall again. The

frog keeps repeating this process, but the intervals between jumps

keep getting half as long: 1/2 second, then 1/4 second, and so on.

In theory, how long will it take to reach the wall, if we start timing

it the moment it ﬁnishes its ﬁrst jump?

(a) More information is needed to answer this question.

(b) 8 seconds.

CHAPTER 14 Growth and Decay 359

, or 16, seconds.

(d) 2

, or 256, seconds.

3. Consider this sum of numbers:

S ¼ 4  4 þ 4  4 þ 4  4 þ 4  4 þ :::

Which of the following statements is true?

(a) S is a convergent series.

(b) S is an arithmetic series.

(d) S is not a series.

4. What is the base-10 logarithm of 0.00001?

(a) e/10

(b) e/10

(d) 5

5. Which of the following points cannot, in theory, be shown on a

log–log (x,y) coordinate system?

(a) The point corresponding to x ¼ 1 and y ¼ 1.

(b) The point corresponding to x ¼ 0 and y ¼ 1.

(d) The point corresponding to x ¼ 0.1 and y ¼ 0.1.

6. What is the natural logarithm of e?

(a) 0

(b) 1

(d) 1/e

7. Suppose a sequence of numbers is such that each value is exactly 4 less

than the value before it. This is an example of

(a) a geometric progression

(b) an arithmetic progression

(d) a fractional progression

8. Suppose you’re listening to a compact disc on your new high-powered

stereo sound system. The VU (volume unit) meter needles are kicking

up to the points marked 0 dB, exactly where the black lines end

and the red lines begin. If you increase the gain so the needles are

kicking up to þ6 dB in the red zone, the sound power coming from

PART 4 Math in Science

360