Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide
Подождите немного. Документ загружается.


(c) Vectors a and b lie along the same straight line.
(d) All of the above statements are true.
7. What is the cross product (2i þ 0j þ 0k) (0i þ 2j þ 0k)?
(a) 0i þ 0j þ 0k
(b) 2i þ 2j þ 0k
(c) 0i þ 0j þ 4k
(d) The scalar 0.
8. What is the sum of the two vectors (3,5) and (5,3)?
(a) (0,0)
(b) (8,8)
(c) (2,2)
(d) (2,2)
9. If a straight line in Cartesian three-space has direction defined by
m ¼ 0i þ 0j þ 3k, we can surmise:
(a) that the line is parallel to the x axis
(b) that the line lies in the yz plane
(c) that the line lies in the xy plane
(d) none of the above
10. Suppose a plane passes through the origin, and a vector normal to
the plane is represented by 4i 5j þ 8k. The equation of this plane is
(a) 4x 5y þ 8z ¼ 0
(b) 4x þ 5y 8z ¼ 7
(c) (x 4) ¼ ( y þ 5) ¼ (z 8)
(d) impossible to determine without more information
CHAPTER 13 Vectors and 3D 331

CHAPTER
14
Growth and Decay
Rates of change can sometimes be expressed in terms of mathematical
constants. In this chapter, we’ll examine a few of the ways this can happen.
Growth by Addition
The simplest changeable quantities can be written as lists of numbers whose
values repeatedly increase or decrease by a fixed amount. Here are some
examples:
A ¼ 1ó 2ó 3ó 4ó 5ó 6
B ¼ 0ó 1ó 2ó 3ó 4ó 5
C ¼ 2ó 4ó 6ó 8
D ¼5ó 10ó 15ó 20
E ¼ 4ó 8ó 12ó 16ó 20ó 24ó 28ó ...
F ¼ 2ó 0ó 2ó 4ó 6ó 8ó 10ó ...
332
Copyright © 2004 by The McGraw-Hill Companies, Inc. Click here for terms of use.

The first four of these sequences are finite. The last two are infinite, as
indicated by the three dots following the last term in each case.
ARITHMETIC PROGRESSION
In each of the six sequences shown above, the values either increase (A, C,
and E) or else they decrease (B, D, and F). In all six sequences, the ‘‘spacing’’
between numbers is constant throughout. Note:
*
The values in A always increase by 1.
*
The values in B always decrease by 1.
*
The values in C always increase by 2.
*
The values in D always decrease by 5.
*
The values in E always increase by 4.
*
The values in F always decrease by 2.
Each sequence has a starting point or first number. After that, succeeding
numbers can be predicted by repeatedly adding a constant. If the added
constant is positive, the sequence increases. If the added constant is negative,
the sequence decreases.
Let s
0
be the first number in a sequence S, and let c be a constant. Imagine
that S can be written in this form:
S ¼ s
0
ó ðs
0
þ cÞó ðs
0
þ 2cÞó ðs
0
þ 3cÞó ...
for as far as the sequence happens to go. Such a sequence is called an
arithmetic sequence or an arithmetic progression. In this context, the word
‘‘arithmetic’’ is pronounced ‘‘air-ith-MET-ick.’’
The numbers s
0
and c can be whole numbers, but that is not a requirement.
They can be fractions such as 2/3 or 7/5. They can be irrational numbers
such as the square root of 2. As long as the separation between any two
adjacent terms in a sequence is the same, the sequence is an arithmetic
progression. In fact, even if s
0
and c are both equal to 0, the resulting
sequence is an arithmetic progression.
ARITHMETIC SERIES
A series is, by definition, the sum of all the terms in a sequence. For any arith-
metic sequence, the corresponding arithmetic series can be defined only if the
sequence is finite. That means it must have a finite number of terms. For the
above sequences A through F, let the corresponding series be called A
þ
CHAPTER 14 Growth and Decay 333

through F
þ
. Then:
A
þ
¼ 1 þ 2 þ 3 þ 4 þ 5 þ 6 ¼ 21
B
þ
¼ 0 þð1Þþð2Þþð3Þþð4Þþð5Þ¼15
C
þ
¼ 2 þ 4 þ 6 þ 8 ¼ 20
D
þ
¼ð5Þþð10Þþð15Þþð20Þ¼50
E
þ
is not defined
F
þ
is not defined
ARITHMETIC INTERPOLATION
When you see a long sequence of numbers, you should be able to tell
without much trouble whether or not it’s an arithmetic sequence. If it isn’t
immediately obvious, you can conduct a test: subtract each number from
the one after it. If all the differences are the same, then the sequence is an
arithmetic sequence.
Imagine that you see a long sequence of numbers, and some of the
intermediate values are missing. An example of such a situation is shown
in Table 14-1. It’s not too hard to figure out what the missing values are, once
you realize that this is an arithmetic sequence in which each term has a
value that is 3 larger than the term preceding it. The 4th term has a value of
14, and the 9th term has a value of 29. The process of filling in missing
intermediate values in a sequence is a form of interpolation. We might call the
process of filling in Table 14-1 arithmetic interpolation.
ARITHMETIC EXTRAPOLATION
It is possible to ‘‘predict’’ what the next numbers are, or would be if a series
were lengthened. Table 14-2 illustrates an example of this type of situation.
Table 14-1 A sequence with some intermediate values missing. They can be filled in
by interpolation.
Position: 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 11th
Value: 5 8 11 ? 17202326? 32 35
PART 4 Math in Science
334
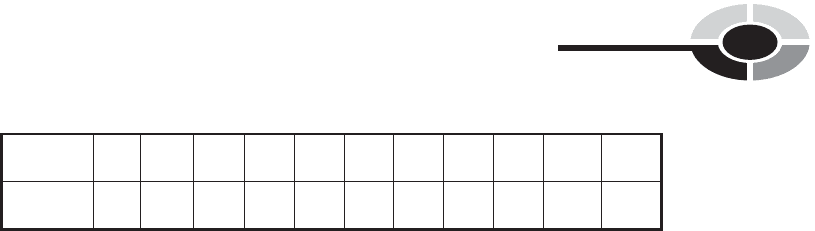
The values keep getting smaller by 2. The 7th number is 20. Therefore, the
8th number must be 18, the 9th number must be 16, the 10th number must
be 14, and the 11th number must be 12. This extension process constitutes
a form of extrapolation, so we can call the process of filling in Table 14-2
arithmetic extrapolation.
PLOTTING AN ARITHMETIC SEQUENCE
An arithmetic sequence looks like a set of points when plotted in Cartesian
(rectangular) coordinates. The term number or position in the sequence
is depicted on the horizontal axis, and it plays the role of the independent
variable. The term value is plotted against the vertical axis, and it plays
the role of the dependent variable.
Figure 14-1 shows examples of two arithmetic sequences as they appear
when graphed. (The dashed lines connect the dots, but they aren’t actually
parts of the sequences.) Note that the dashed lines are straight. One sequence
is increasing, and the dashed line connecting this set of points ramps upward
as you go toward the right. Because this sequence is finite, the dashed line
ends at the final point (6,6). The other sequence is decreasing, and the dashed
line for it ramps downward as you go toward the right. This sequence is
infinite, as shown by the three dots at the end of the string of numbers, and
also by the arrow at the right-hand end of the dashed line.
When any arithmetic sequence is graphed in this way, its points lie along a
straight line. The slope m of the line depends on whether the sequence
increases (positive slope) or decreases (negative slope). In fact, m is exactly
equal to the constant c.
BE CAREFUL!
When interpolating or extrapolating any sequence, you must be sure to check
out enough values to know that you’re looking at a true sequence, and not
just a string of numbers. If the string has only two or three values that
increase by the same amount, you don’t have enough information to be
Table 14-2 Extension of an arithmetic sequence can be done by extrapolation.
Position: 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 11th
Value: 32 30 28 26 24 22 20 ? ? ? ?
CHAPTER 14 Growth and Decay 335

sure you’re observing an arithmetic sequence. You need at least four or five
values.
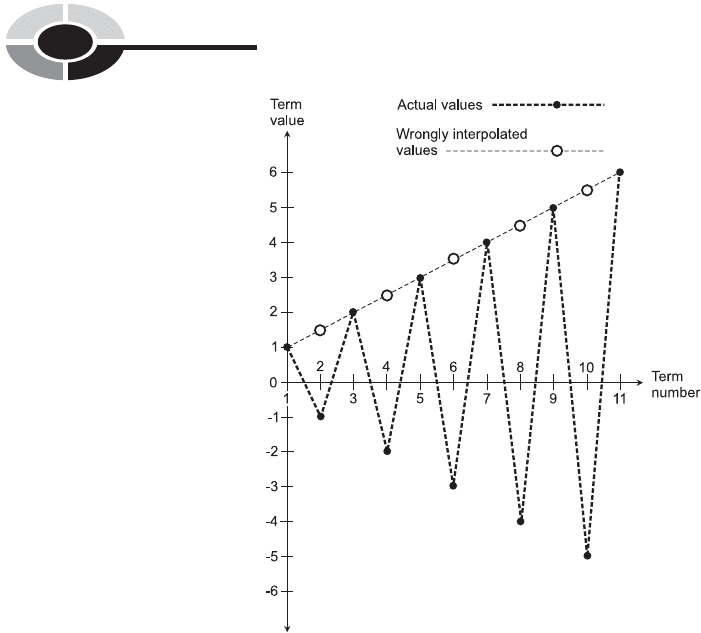
There’s another way to go wrong when attempting to interpolate a
sequence. If the missing values are alternate numbers, you can be deceived.
The examples in Tables 14-3A, B, and C provide a vivid illustration of how
far astray you can go if you jump to conclusions about filling in a sequence
with alternate terms missing! The plot in Fig. 14-2 illustrates this graphically.
PROBLEM 14-1
Consider again the general formula for an arithmetic sequence S:
S ¼ s
0
ó ðs
0
þ cÞó ðs
0
þ 2cÞó ðs
0
þ 3cÞó ...
Suppose s
0
¼ 5 and c ¼ 3. List the first 10 terms of an infinite sequence that
follows this form and has these values.
Fig. 14-1. When the values of the terms in an arithmetic sequence are plotted in rectangular
coordinates, the points always fall along straight lines.
PART 4 Math in Science
336

SOLUTION 14-1
The first number is 5, and the numbers increase by 3 every time thereafter. So:
S ¼ 5ó 8ó 11ó 14ó 17ó 20ó 23ó 26ó 29ó 32ó ...
PROBLEM 14-2
Is the following sequence an arithmetic sequence? If so, what are the values s
0
(the starting value) and c (the constant of change)?
S ¼ 2ó 4ó 8ó 16ó 32ó 64ó ...
SOLUTION 14-2
This is not an arithmetic sequence. The numbers do not increase at a steady
rate. There is a pattern, however: each number in the sequence is twice as
large as the number before it. We’ll look at this type of series shortly.
PROBLEM 14-3
Is the following sequence an arithmetic sequence? If so, what are the values s
0
(the starting value) and c (the constant of change)?
S ¼ 100ó 135ó 170ó 205ó 240ó 275ó 310ó ...
Table 14-3
(A) Suppose you see a sequence with alternate values missing, like this:
Position: 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 11th
Value: 12345 6
(B) It’s tempting to think that it is an arithmetic sequence, and that the missing values
should be filled in to get this:
Position: 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 11th
Value: 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
(C) But in reality, it is not an arithmetic sequence. Instead, it goes like this:
Position: 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 11th
Value: 1 –1 2 –2 3 –3 4 –4 5 –5 6
CHAPTER 14 Growth and Decay 337
SOLUTION 14-3
This is an arithmetic sequence, at least for the numbers shown (the first seven
terms). In this case, s
0
¼ 100 and c ¼ 35.
Growth by Multiplication
Another type of progression has values that are repeatedly multiplied by
some constant. Here are a few examples:
G ¼ 1ó 2ó 4ó 8ó 16ó 32
H ¼ 1ó 1ó 1ó 1ó 1ó 1ó ...
I ¼ 1ó 10ó 100ó 1000
J ¼5ó 15ó 45ó 135ó 405
K ¼ 3ó 9ó 27ó 81ó 243ó 729ó 2187ó ...
L ¼ 1=2ó 1=4ó 1=8ó 1=16ó 1= 32ó ...
Fig. 14-2. Graphical portrayal of mistaken interpolation.
PART 4 Math in Science
338

Sequences G, I, and J are finite. Sequences H, K, and L are infinite, as
indicated by the three dots following the last term in each sequence.
GEOMETRIC PROGRESSION
Examine the six sequences above. Upon casual observation, they appear to
be much different from one another. But in all six sequences, each term is
a specific and constant multiple of the term before it. Note:
*
The values in G progress by a constant factor of 2.
*
The values in H progress by a constant factor of –1.
*
The values in I progress by a constant factor of 10.
*
The values in J progress by a constant factor of 3.
*
The values in K progress by a constant factor of 3.
*
The values in L progress by a constant factor of 1/2.
Each sequence has a starting point or first number. After that, succeeding
numbers are generated by repeated multiplication by a constant. If the con-
stant is positive, the values in the sequence stay ‘‘on the same side of 0’’ (they
either remain positive or remain negative). If the constant is negative,
the values in the sequence ‘‘alternate to either side of 0’’ (if a given term is
positive, the next is negative, and if a given term is negative, the next is
positive).
Let t
0
be the first number in a sequence T, and let k be a constant. Imagine
that T can be written in this form:
T ¼ t
0
ó t
0
kó t
0
k
2
ó t
0
k
3
ó t
0
k
4
ó ...
for as long as the sequence goes. Such a sequence is called a geometric
sequence or a geometric progression.
If k happens to be equal to 1, the sequence consists of the same number,
listed over and over. If k ¼1, the sequence alternates between t
0
and its
negative. If t
0
is less than 1 or greater than 1, the values get farther and
farther from 0. If t
0
is between (but not including) 1 and 1, the values get
closer and closer to 0. If t
0
¼ 1ort
0
¼1, the values stay the same distance
from 0.
The numbers t
0
and k can be whole numbers, but this is not a requirement.
As long as the multiplication factor between any two adjacent terms in a
sequence is the same, the sequence is a geometric progression. In the last
sequence, k ¼ 1/2. This is an especially interesting sequence, as we’ll see in a
moment.
CHAPTER 14 Growth and Decay 339

GEOMETRIC SERIES
For a geometric sequence, the corresponding geometric series, which is
the sum of all the terms, can always be defined if the sequence is finite.
Sometimes the sum of all the terms can be defined even if the sequence is
infinite.
For the above sequences G through L, let the corresponding series be
called G
þ
through L
þ
. Then:
G
þ
¼ 1 þ 2 þ 4 þ 8 þ 16 þ 32 ¼ 63
H
þ
¼ 1 1 þ 1 1 þ 1 1 þ ... ¼ ?
I
þ
¼ 1 þ 10 þ 100 þ 1000 ¼ 1111
J
þ
¼5 15 45 135 405 ¼605
K
þ
¼ ‘‘blows up’’ and is not defined
L
þ
¼ 1=2 þ 1=4 þ 1=8 þ 1=16 þ 1=32 þ ... ¼ ?
The finite series G
þ
, I
þ
, and J
þ
are straightforward enough. The infinite series
H
þ
seems unable to settle on 0 or 1, repeatedly hitting both. It’s tempting to
say that H
þ
is a number with two values at once, and a fascinating theory can
be built around the notion of multi-valued numbers. But in conventional
math, we have to say that H
þ
is not definable as a number. The infinite series
K
þ
runs off ‘‘out of control’’ and is an example of a divergent series, because
its values keep on getting farther and farther away from 0 without limit.
That leaves us with L
þ
. What’s going on with this series?
PARTIAL SUMS
When we have an infinite sequence and we start to add up its numbers, we get
another sequence of numbers representing the sums. These sums are called
partial sums. For the above sequences H, K, and L, the partial sums, which
we will denote using asterisk superscripts instead of plus-sign subscripts, go
like this:
H ¼ 1ó 1ó 1ó 1ó 1ó 1ó ...
H
¼ 1ó 0ó 1ó 0ó 1ó 0ó ...
K ¼ 3ó 9ó 27ó 81ó 243ó 729ó 2187ó ...
K
¼ 3ó 12ó 39ó 120ó 363ó 1092ó 3279ó ...
L ¼ 1=2ó 1=4ó 1=8ó 1=16ó 1=32ó ...
L
¼ 1=2ó 3=4ó 7=8ó 15=16ó 31=32ó ...
PART 4 Math in Science
340
