Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

FREQUENCY DISTRIBUTION

In both of the above examples (the ﬁrst showing the results of 6000 die tosses

and the second showing the days with precipitation in ﬁve hypothetical

towns), the scenarios are portrayed with frequency as the dependent variable.

This is true of the tables as well as the graphs. Whenever frequency is

Fig. 7-4. Measurable precipitation during a hypothetical year, in ﬁve diﬀerent

imaginary towns.

Fig. 7-5. Relative energy available from sunlight, per day, during the course of a calendar

year at a hypothetical location.

CHAPTER 7 A Statistics Sampler 151

portrayed as the dependent variable in a distribution, that distribution is

called a frequency distribution.

Suppose we complicate the situation involving dice. Instead of one person

tossing one die 6000 times, we have ﬁve people tossing ﬁve diﬀerent dice, and

each person tosses the same die 6000 times. The dice are colored red, orange,

yellow, green, and blue, and are manufactured by ﬁve diﬀerent companies,

called Corp. A, Corp. B, Corp. C, Corp. D, and Corp. E, respectively. Four

of the dice are ‘‘weighted’’ and one is not. There are thus 30,000 die tosses to

tabulate or graph in total. When we conduct this experiment, we can tabulate

the data in at least two ways.

Ungrouped frequency distribution

The simplest way to tabulate the die toss results as a frequency distribution is

to combine all the tosses and show the total frequency for each die face 1

through 6. A hypothetical example of this result, called an ungrouped

frequency distribution, is shown in Table 7-3. We don’t care about the weight-

ing characteristics of each individual die, but only about potential biasing

of the entire set. It appears that, for this particular set of dice, there is

some bias in favor of faces 4 and 6, some bias against faces 1 and 3, and little

or no bias either for or against faces 2 and 5.

Table 7-3 An ungrouped frequency distribution showing

the results of a single, hypothetical experiment in which ﬁve

diﬀerent dice, some ‘‘weighted’’ and some not, are each

tossed 6000 times.

Face of die Toss results

for all die

1 4857

2 4999

3 4626

4 5362

5 4947

6 5209

PART 2 Finding Unknowns

152

Grouped frequency distribution

If we want to be more detailed, we can tabulate the frequency for each die

face 1 through 6 separately for each die. A hypothetical product of this eﬀort,

called a grouped frequency distribution, is shown in Table 7-4. The results are

grouped according to manufacturer and die color. From this distribution, it is

apparent that some of the dice are heavily ‘‘weighted.’’ Only the green die,

manufactured by Corp. D, seems to lack any bias. If you are astute, you

will notice (or at least strongly suspect) that the green die here is the same

die, with results gathered from the same experiment, as is portrayed in

Table 7-1 and Fig. 7-3.

PROBLEM 7-1

Suppose you add up all the numbers in each column of Table 7-4. What

should you expect, and why? What should you expect if the experiment is

repeated many times?

SOLUTION 7-1

Each column should add up to 6000. This is the number of times each die

(red, orange, yellow, green, or blue) is tossed in the experiment. If the

sum of the numbers in any of the columns is not equal to 6000, then the

Table 7-4 A grouped frequency distribution showing the results of a

single, hypothetical experiment in which ﬁve diﬀerent dice, some

‘‘weighted’’ and some not, and manufactured by ﬁve diﬀerent

companies, are each tossed 6000 times.

Face of die Toss results by manufacturer

Red

Corp. A

Orange

Corp. B

Yellow

Corp. C

Green

Corp. D

Blue

Corp. E

1 625 1195 1689 968 380

2 903 1096 1705 1027 268

3 1300 890 1010 1018 408

4 1752 787 540 996 1287

5 577 1076 688 1007 1599

6 843 956 368 984 2058

CHAPTER 7 A Statistics Sampler 153

experiment was done in a faulty way, or else there is an error in the com-

pilation of the table. If the experiment is repeated many times, the sums of

the numbers in each column should always be 6000.

PROBLEM 7-2

Suppose you add up all the numbers in each row of Table 7-4. What should

you expect, and why? What should you expect if the experiment is repeated

many times?

SOLUTION 7-2

The sums of the numbers in the rows will vary, depending on the bias of the

set of dice considered as a whole. If, taken all together, the dice show any

bias, and if the experiment is repeated many times, the sums of the numbers

should be consistently lower for some rows than for other rows.

PROBLEM 7-3

Each small rectangle in a table, representing the intersection of one row

with one column, is called a cell of the table. What do the individual numbers

in the cells of Table 7-4 represent?

SOLUTION 7-3

The individual numbers are absolute frequencies. They represent the actual

number of times a particular face of a particular die came up during the

course of the experiment.

More Definitions

Here are some more deﬁnitions you should learn in order to get comfortable

reading or talking about statistics.

CUMULATIVE ABSOLUTE FREQUENCY

When data are tabulated, the absolute frequencies are often shown in one or

more columns. Look at Table 7-5, for example. This shows the results of the

tosses of the blue die in the experiment we looked at a while ago. The ﬁrst

column shows the number on the die face. The second column shows the

absolute frequency for each face, or the number of times each face turned

up during the experiment. The third column shows the cumulative absolute

frequency, which is the sum of all the absolute frequency values in table

cells at or above the given position.

PART 2 Finding Unknowns

154

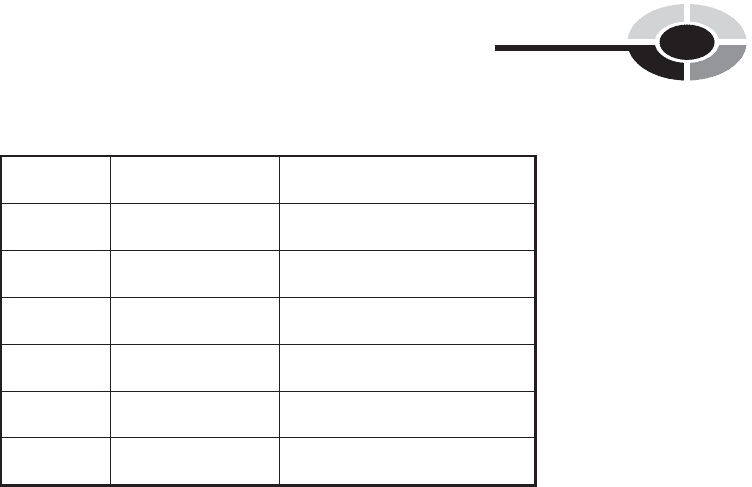
The cumulative absolute frequency numbers in a table always ascend

(increase) as you go down the column. The highest cumulative absolute

frequency value should be equal to the sum of all the individual absolute

frequency numbers. In this instance, it is 6000, the number of times the blue

die was tossed.

CUMULATIVE RELATIVE FREQUENCY

Relative frequency values can be added up down the columns of a table, in

exactly the same way as the absolute frequency values are added up. When

this is done, the resulting values, usually expressed as percentages, show

the cumulative relative frequency.

Examine Table 7-6. This is a more detailed analysis of what happened with

the blue die in the above-mentioned experiment. The ﬁrst, second, and fourth

columns in Table 7-6 are identical with the ﬁrst, second, and third columns in

Table 7-5. The third column in Table 7-6 shows the percentage represented

by each absolute frequency number. These percentages are obtained by

dividing the number in the second column by 6000, the total number of

tosses. The ﬁfth column shows the cumulative relative frequency, which is

the sum of all the relative frequency values in table cells at or above the given

position.

The cumulative relative frequency percentages in a table, like the

cumulative absolute frequency numbers, always ascend as you go down

Table 7-5 Results of an experiment in which a ‘‘weighted’’ die is tossed 6000 times,

showing absolute frequencies and cumulative absolute frequencies.

Face of die Absolute frequency Cumulative absolute frequency

1 380 380

2 268 648

3 408 1056

4 1287 2343

5 1599 3942

6 2058 6000

CHAPTER 7 A Statistics Sampler 155

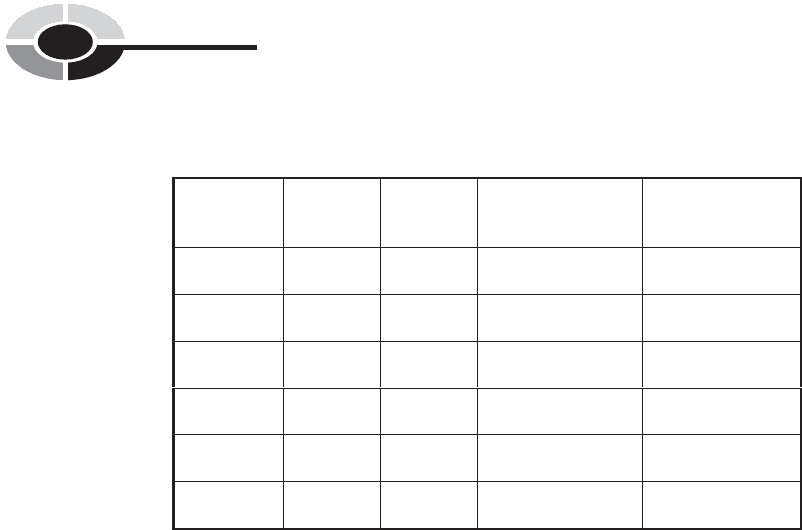
the column. The total cumulative relative frequency should be equal to

100%. In this sense, the cumulative relative frequency column in a table can

serve as a checksum, helping to ensure that the entries have been tabulated

correctly.

MEAN

The mean for a discrete variable in a distribution is the mathematical average

of all the values. If the variable is considered over the entire population,

the average is called the population mean. If the variable is considered

over a particular sample of a population, the average is called the sample

mean. There can be only one population mean for a population, but

there can be many diﬀerent sample means. The mean is often denoted by

the lowercase Greek letter mu, in italics (). Sometimes it is also denoted

by an italicized lowercase English letter, usually x, with a bar (vinculum)

over it.

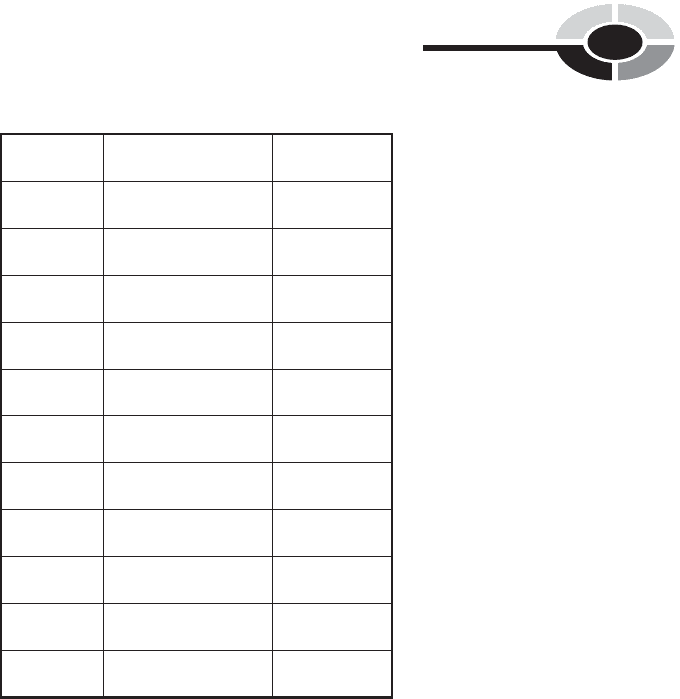
Table 7-7 shows the results of a 10-question test, given to a class of 100

students. As you can see, every possible score is accounted for. There are

some people who answered all 10 questions correctly; there are some who

did not get a single answer right. In order to determine the mean score for

the whole class on this test – that is, the population mean, called 

–we

must add up the scores of each and every student, and then divide by 100.

Table 7-6 Results of an experiment in which a ‘‘weighted’’ die is tossed 6000

times, showing absolute frequencies, relative frequencies, cumulative absolute

frequencies, and cumulative relative frequencies.

Face of die Absolute

frequency

Relative

frequency

Cumulative

absolute frequency

Cumulative

relative frequency

1 380 6.33% 380 6.33%

2 268 4.47% 648 10.80%

3 408 6.80% 1056 17.60%

4 1287 21.45% 2343 39.05%

5 1599 26.65% 3942 65.70%

6 2058 34.30% 6000 100.00%

PART 2 Finding Unknowns

156

First, let’s sum the products of the numbers in the ﬁrst and second columns.

This will give us 100 times the population mean:

ð10  5Þþð9  6Þþð8  19Þþð7  17Þþð6  18Þþð5  11Þ

þð4  6Þþð3  4Þþð2  4Þþð1  7Þþð0  3Þ

¼ 50 þ 54 þ 152 þ 119 þ 108 þ 55 þ 24 þ 12 þ 8 þ 7 þ 0

¼ 589

Dividing this by 100, the total number of test scores (one for each student

who turns in a paper), we obtain 

¼ 589/100 ¼ 5.89.

The teacher in this class has assigned letter grades to each score. Students

who scored 9 or 10 correct received grades of A; students who got scores of 7

or 8 received grades of B; those who got scores of 5 or 6 got grades of C;

those who got scores of 3 or 4 got grades of D; those who got less than 3

correct answers received grades of F. The assignment of grades, informally

known as the ‘‘curve,’’ is a matter of teacher temperament and doubtless

Table 7-7 Scores on a 10-question test taken by 100 students.

Test score Absolute frequency Letter grade

10 5 A

96 A

819 B

717 B

618 C

511 C

46 D

34 D

24 F

17 F

03 F

CHAPTER 7 A Statistics Sampler 157

would seem arbitrary to the students who took this test. (Some people might

consider the ‘‘curve’’ in this case to be overly lenient, while a few might think

it is too severe.)

PROBLEM 7-4

What are the sample means for each grade in the test whose results are

tabulated in Table 7-7? Use rounding to determine the answers to two

decimal places.

SOLUTION 7-4

Let’s call the sample means 

for the grade of A, 

for the grade of B, and

so on down to 

for the grade of F.

To calculate 

, note that 5 students received scores of 10, while 6

students got scores of 9, both scores good enough for an A. This is a total of

5 þ 6, or 11, students getting the grade of A. Therefore:



¼½ð5  10Þþð6  9Þ=11

¼ð50 þ 54Þ=11

¼ 104=11

¼ 9:45

To ﬁnd 

, observe that 19 students scored 8, and 17 students scored 7.

Thus, 19 þ 17, or 36, students received grades of B. Calculating:



¼½ð19  8Þþð17  7Þ=36

¼ð152 þ 119Þ=36

¼ 271=36

¼ 7:53

To determine 

, check the table to see that 18 students scored 6, while 11

students scored 5. Therefore, 18 þ 11, or 29, students did well enough for

a C. Grinding out the numbers yields this result:



¼½ð18  6Þþð11  5Þ=29

¼ð108 þ 55Þ=29

¼ 163=29

¼ 5:62

PART 2 Finding Unknowns

158

To calculate 

, note that 6 students scored 4, while 4 students scored 3.

This means that 6 þ 4, or 10, students got grades of D:



¼½ð6  4Þþð4  3Þ=10

¼ð24 þ 12Þ=10

¼ 36=10

¼ 3:60

Finally, we determine 

. Observe that 4 students got scores of 2,

7 students got scores of 1, and 3 students got scores of 0. Thus, 4 þ 7 þ 3, or

14, students failed the test:



¼½ð4  2Þþð7  1Þþð3  0Þ=14

¼ð8 þ 7 þ 0Þ=14

¼ 15=14

¼ 1:07

MEDIAN

If the number of elements in a distribution is even, then the median is the

value such that half the elements have values greater than or equal to it,

and half the elements have values less than or equal to it. If the number of

elements is odd, then the median is the value such that the number of

elements having values greater than or equal to it is the same as the number

of elements having values less than or equal to it. The word ‘‘median’’ is

synonymous with ‘‘middle.’’

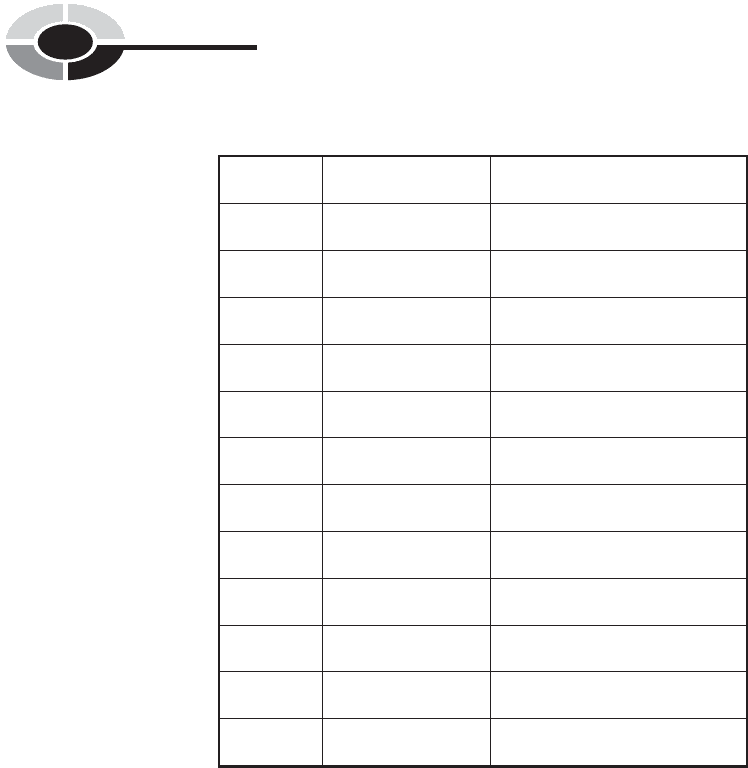
Table 7-8 shows the results of the 10-question test described above, but

instead of showing letter grades in the third column, the cumulative absolute

frequency is shown instead. The tally is begun with the top-scoring papers

and proceeds in order downward. (It could just as well be done the other way,

starting with the lowest-scoring papers and proceeding upward.) When the

scores of all 100 individual papers are tallied this way, so they are in order,

the scores of the 50th and 51st papers – the two in the middle – are found to

be 6 correct. Thus, the median score is 6, because half the students scored 6 or

above, and the other half scored 6 or below.

It’s possible that in another group of 100 students taking this same test, the

50th paper would have a score of 6 while the 51st paper would have a score

of 5. When two values ‘‘compete,’’ the median is equal to their average.

In this case it would be midway between 5 and 6, or 5.5.

CHAPTER 7 A Statistics Sampler 159

MODE

The mode for a discrete variable is the value that occurs the most often. In the

test whose results are shown in Table 7-7, the most ‘‘popular’’ or often-

occurring score is 8 correct answers. There were 19 papers with this score.

No other score had that many results. Therefore, the mode in this case is 8.

Suppose that another group of students took this test, and there were two

scores that occurred equally often? For example, suppose 16 students got 8

answers right, and 16 students also got 6 answers right? In this case there are

two modes: 6 and 8. This distribution would be called a bimodal distribution.

It’s even possible that three scores would be equally popular, resulting in a

trimodal distribution.

Now imagine there are only 99 students in a class, and there are exactly

9 students who get each of the 11 possible scores (from 0 to 10 correct answers).

Table 7-8 The median can be determined by tabulating the cumulative

absolute frequencies.

Test score Absolute frequency Cumulative absolute frequency

10 5 5

96 11

819 30

717 47

6 (partial) 3 50

6 (partial) 15 65

511 76

46 82

34 86

24 90

17 97

0 3 100

PART 2 Finding Unknowns

160