Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide
Подождите немного. Документ загружается.

34. One millionth of a kilometer is equal to
(a) 1 meter
(b) 10 meters
(c) 1 millimeter
(d) 10 millimeters
(e) 1 micrometer
35. In a graph intended to show the correlation between two variables,
strong negative correlation is indicated by points that
(a) all lie near a horizontal line
(b) all lie near a vertical line
(c) are scattered all over the graph
(d) all lie tightly clustered near the center of the graph
(e) are arranged in some manner other than the four described
above
36. Suppose you are performing calculations on a computer, and you
end up with the expression 5.000000000E45. This is
(a) a number between 0 and 1
(b) a number greater than 1
(c) a number between 1 and 0
(d) a number less than 1
(e) a number too large to be defined
37. The reciprocal of 5.000000000E45 can be expressed as
(a) 2 10
44
(b) 2 10
44
(c) 5 10
45
(d) 5 10
44
(e) none of the above
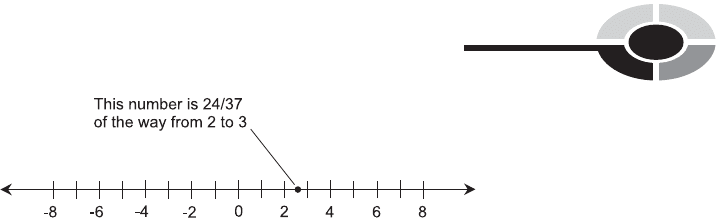
38. In Fig. Test 1-5, the solid curve represents an approximation of stock
price versus time, based on points plotted
(a) continuously
(b) at regular time intervals
Fig. Test 1-4. Illustration for Part One Test Question 32.
Test: Part 1 101
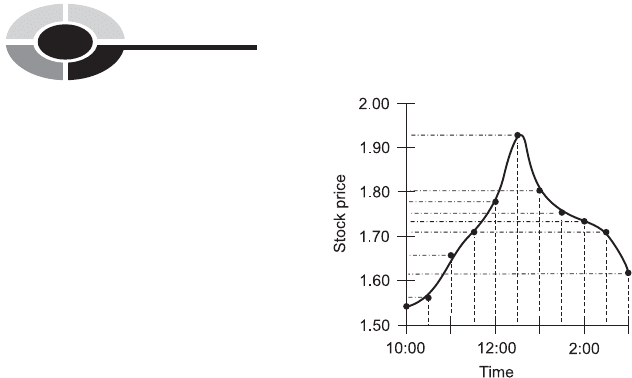
(c) at regular stock-price intervals
(d) at random
(e) by extrapolation
39. In Fig. Test 1-5, suppose stock price is considered as a function of
time. We can call this
(a) a nondecreasing function
(b) a nonincreasing function
(c) both a nondecreasing and a nonincreasing function
(d) neither a nondecreasing nor a nondecreasing function
(e) a relation, but not a legitimate function
40. In the hexadecimal number system, the single-digit numerals are
(a) 1 and 2
(b) 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10
(c) 1, 2, 3, 4, 5, 6, 7, and 8
(d) 1, 2, 3, and 4
(e) none of the above
Fig. Test 1-5. Illustration for Part One Test Questions 38 and 39.
PART 1 Expressing Quantities
102

PART TWO
Finding Unknowns
103
Copyright © 2004 by The McGraw-Hill Companies, Inc. Click here for terms of use.
This page intentionally left blank

CHAPTER
5
Basic Algebra
Linear equations have variables that are not raised to any power (except 1 or 0).
They are the simplest equations to solve, although when there are four or more
linear equations in four or more variables, the solution process can be messy.
In this chapter, we’ll deal with linear equations in one and two variables.
Single-Variable Linear Equations
The objective of solving a single-variable equation is to get it into a form
where the expression on the left-hand side of the equality symbol is exactly
equal to the variable being sought (for example, x), and a defined expression
not containing that variable is on the right.
ELEMENTARY RULES
There are several ways in which an equation in one variable can be manipu-
lated to obtain a solution, assuming a solution exists. Any and all of the
105
Copyright © 2004 by The McGraw-Hill Companies, Inc. Click here for terms of use.

principles outlined in Chapter 1 can be applied toward this result. In addi-
tion, the following rules can be applied in any order, and any number of
times.
Addition of a quantity to each side: Any defined constant, variable, or
expression can be added to both sides of an equation, and the result is
equivalent to the original equation.
Subtraction of a quantity from each side: Any defined constant, variable,
or expression can be subtracted from both sides of an equation, and the result
is equivalent to the original equation.
Multiplication of each side by a nonzero quantity: Both sides of an equation
can be multiplied by a nonzero constant, variable, or expression, and the
result is equivalent to the original equation.
Division of each side by a quantity: Both sides of an equation can be divided
by a nonzero constant, by a variable that cannot attain a value of zero, or
by an expression that cannot attain a value of zero over the range of its
variable(s), and the result is equivalent to the original equation.
BASIC EQUATION IN ONE VARIABLE
Consider an equation of the following form:
ax þ b ¼ cx þ d
where a, b, c, and d are real numbers, and a 6¼ c. This equation is solved as
follows:
ax þ b ¼ cx þ d
ax ¼ cx þ d b
ax cx ¼ d b
ða cÞx ¼ d b
x ¼ðd bÞ=ða cÞ
STANDARD FORM
Any single-variable linear equation can be reduced to this form, called the
standard form:
ax þ b ¼ 0
PART 2 Finding Unknowns
106
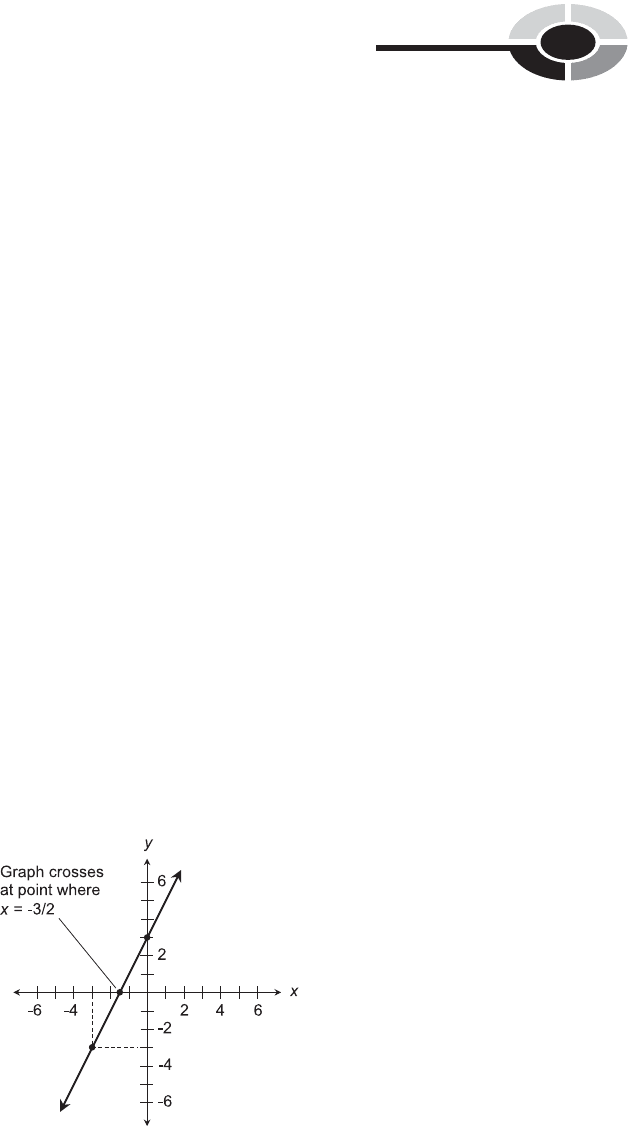
where a and b are constants, and x is the variable. The value on the right-
hand side of the equals sign is always 0 when a linear equation is in standard
form.
ILLUSTRATING THE SOLUTION
Suppose we substitute y for 0 in the standard form of a linear equation.
This produces a relation where y is the dependent variable and x is the
independent variable:
ax þ b ¼ y
Let’s create a graph of this relation for particular values of a and b, say a ¼ 2
and b ¼ 3, so the linear equation is
2x þ 3 ¼ y
Put the x-values on the horizontal axis and the y-values on the vertical axis.
Plot several test points by setting x at certain values, calculating the y values
that result, and then plotting the points on the graph. You should get
something that looks like Fig. 5-1. The graph is a straight line. Try this for
several different combinations of constants a and b. You will find that
the graph always turns out as a straight line. That’s where the term ‘‘linear
equation’’ comes from!
The solution to the single-variable equation ax þ b ¼ 0 is indicated by the
point where the straight-line graph for ax þ b ¼ y crosses the x axis (that is,
Fig. 5-1. When the equation 2x þ 3 ¼ y is plotted as a graph, it turns out to be a straight line.
CHAPTER 5 Basic Algebra 107

the horizontal axis). That is, it is the value of x for the particular case where
y ¼ 0. In Fig. 5-1, this happens to be x ¼3/2.
PROBLEM 5-1
Solve the following equation for x. Show the results on a graph similar
to Fig. 5-1, by replacing the 0 on the right-hand side of the equation by
the variable y.
4x þ 3 ¼ 0
SOLUTION 5-1
To solve 4x þ 3 ¼ 0, proceed like this:
4x þ 3 ¼ 0
4x ¼3 ðsubtract 3 from each sideÞ
x ¼3=4 ðdivide each side by 4Þ
The graph of the equation 4x þ 3 ¼ y is shown in Fig. 5-2. Note where the
straight line crosses the x axis.
PROBLEM 5-2
Solve the following equation for x. Show the results on a graph similar
to Fig. 5-1, by reducing the equation to the standard form ax þ b ¼ 0,
and then replacing the 0 on the right-hand side of the equation by the
variable y.
7x 4 ¼ 3x þ 1
Fig. 5-2. Illustration for Problem 5-1.
PART 2 Finding Unknowns
108

SOLUTION 5-2
To solve 7x 4 ¼ 3x þ 1, proceed like this:
7x 4 ¼ 3x þ 1
7x ¼ 3x þ 5 ðadd 4 to each sideÞ
4x ¼ 5 ðsubtract 3x from each sideÞ
x ¼ 5=4 ðdivide each side by 4Þ
To reduce the equation to the standard form, proceed this way:
7x 4 ¼ 3x þ 1
4x 4 ¼ 1 ðsubtract 3x from each side Þ
4x 5 ¼ 0 ðsubtract 1 from each sideÞ
The graph of the equation 4x 5 ¼ y is shown in Fig. 5-3. Note where the
straight line crosses the x axis; this shows the solution x ¼ 5/4.
PROBLEM 5-3
Solve the following equation for x. Show the results on a graph similar
to Fig. 5-1, by replacing the 0 on the right-hand side of the equation by
the variable y.
2x 4 ¼ 3x
Fig. 5-3. Illustration for Problem 5-2.
CHAPTER 5 Basic Algebra 109
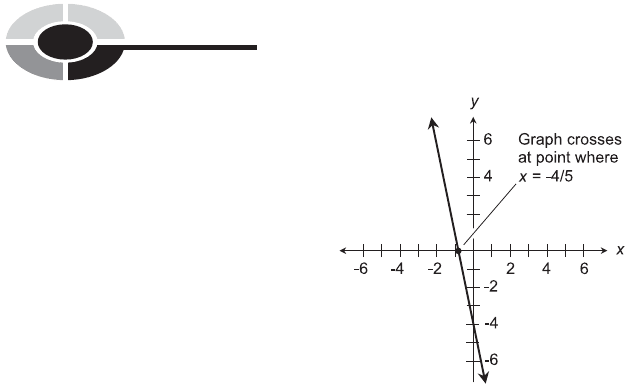
SOLUTION 5-3
To solve 2x 4 ¼ 3x, proceed like this:
2x 4 ¼ 3x
4 ¼ 5 x ðadd 2x to each sideÞ
4=5 ¼ x ðdivide each side by 6Þ
x ¼4=5 ðswitch sidesÞ
To reduce the equation to the standard form, perform this single step:
2x 4 ¼ 3x
5x 4 ¼ 0 ðsubtract 3x from each sideÞ
The graph of the equation 5x 4 ¼ y is shown in Fig. 5-4. Note where
the straight line crosses the x axis; this shows the solution x ¼4/5.
Two-by-Two Linear Equations
A pair of linear equations in two variables, called a two-by-two (2 2) set of
linear equations, takes the following general form:
a
1
x þ b
1
y þ c
1
¼ 0
a
2
x þ b
2
y þ c
2
¼ 0
where x and y represent the variables, and the a’s, b’s, and c’s represent
constants.
Fig. 5-4. Illustration for Problem 5-3.
PART 2 Finding Unknowns
110
