Geiser J. Decomposition Methods for Differential Equations: Theory and Applications

Подождите немного. Документ загружается.

Numerical Experiments 167

We deal with a ﬁrst-order partial diﬀerential equation given as a transport

equation in the following:

∂

= −v

∂

− λu

, for (x, t) ∈ [0,X] × [0,T], (6.67)

∂

= −v

∂

+ λu

, for (x, t) ∈ [0,X] × [0,T], (6.68)

(x, 0) =

1, 0.1 ≤ x ≤ 0.3

0, otherwise

, (6.69)

(x, 0) = 0, for x ∈ [0,X], (6.70)

(0,t)=u

(0,t)=0, for t ∈ [0,T], (6.71)

where λ ∈ R

and v

∈ R

. We have the time interval t ∈ [0,T]andthe

space interval x ∈ [0,X]. We apply the equations with X =1.5andT =1.0.

We rewrite the equation system (6.67)–(6.71) in operator notation, and end

up with the following equations:

∂

u = Au + Bu, (6.72)

u(x, 0) =

(1, 0)

, 0.1 ≤ x ≤ 0.3

(0, 0)

, otherwise

where u =(u

)

Our split operators are

A =



−v

∂

0 −v

∂



,B=



−λ 0

λ 0



. (6.73)

We use the ﬁnite diﬀerence method as a spatial discretization method and

solve the time discretization analytically.

For the spatial discretization, we consider the interval x ∈ [0, 1.5] uniformly

partitioned with a step size of Δx =0.1. For the transport term, we use an

upwind ﬁnite diﬀerence discretization given as

∂

− u

i−1

Δx

. (6.74)

We use the given impulses for the initial values:

(x)=

1, 0.1 ≤ x ≤ 0.3

0, otherwise

, (6.75)

and

(x)=0,x∈ [0, 1.5]. (6.76)

We deal with two indices for the discretized equation for the iterative

operator-splitting method and its application to our transport equation. In-

dex i denotes the spatial discretization, and index j denotes the number of

iteration steps.

168Decomposition Methods for Diﬀerential Equations Theory and Applications

We ﬁrst solve all the equations with index i, that means all 16 equations for

each point. We then apply our iteration steps to arrive at the ﬁrst time-step.

We ﬁnish for one time partition, and we repeat this process four times more

for the computations of ﬁve partitions, an so forth.

In the following equations, we write the iterative operator-splitting algo-

rithm by taking into account the discretization in space. The discretization

in time is solved analytically. For the time interval [t

n+1

], we solve the

following problems consecutively for j =1, 3, 5,.... The split approximation

atthetimelevelt = t

n+1

is deﬁned as u

n+1

≡ u

i,iter

n+1

We have the following algorithm:

∂

1,i,j

= −v

/Δx(u

1,i,j

− u

1,i−1,j

) − λu

1,i,j−1

, (6.77)

∂

2,i,j

= −v

/Δx(u

2,i,j

− u

2,i−1,j

)+λu

1,i,j−1

, (6.78)

∂

1,i,j+1

= −v

/Δx(u

1,i,j

− u

1,i−1,j

) − λu

1,i,j+1

, (6.79)

∂

2,i,j+1

= −v

/Δx(u

2,i,j

− u

2,i−1,j

)+λu

1,i,j+1

, (6.80)

1,i,j

(0) =

1, for i =1, 2, 3

0, otherwise

, (6.81)

2,i,j

(0) = 0, for i =0,...,15, (6.82)

where λ =0.5andv

=0.5andv

=1.0. For the time interval we use

t ∈ [0, 1].

The analytical solution of the equation system (6.77)–(6.82) is

(x, t)=

exp(−λt), for 0.1+v

t ≤ x ≤ 0.3+v

0, otherwise

, (6.83)

and

(x, t)=λ(L

1,2

+ L

2,2

+ M

12,2

), (6.84)

1,2

−

exp(−λt), for 0.1+v

t ≤ x ≤ 0.3+v

0, otherwise

, (6.85)

2,2

, for 0.1+v

t ≤ x ≤ 0.3+v

0, otherwise

, (6.86)

12,2

⎧

⎪

⎨

⎪

⎩

exp(−λt), for 0.1+v

t ≤ x ≤ 0.1+v

−

exp(−λt)·

exp



− (

−v

)·

(x − v

t − 0.3)



, for 0.3+v

t ≤ x ≤ 0.3+v

0, otherwise

. (6.87)

Numerical Experiments 169

For the end time t

end

= 1, we check the results for the end point x

= v

t+0.3.

We obtain the exact solution of our equation:

end

)=0.60653,u

end

)=0.

In Table 6.39 we present the errors, computed with the L

∞

-norm, for the

numerical and exact solutions at the end time t =1andendpointx =

t +0.3=0.8. The experiments are programmed in MATLAB 7.0 and

computed with a 2 GHz Linux personal computer with a calculation accuracy

of about 10

−313

TABLE 6.39: Numerical results for the ﬁrst example using

iterative splitting method.

Number of Iteration err

∞

err

∞

time partitions n steps j

1 2 2.679116 × 10

−1

2.465165 × 10

−1

1 4 1.699365 × 10

−1

3.584424 × 10

−1

1 10 2.702681 ×10

−2

5.327567 × 10

−2

5 2 2.472959 × 10

−1

6.812055 × 10

−2

5 4 1.181408 × 10

−1

4.757047 × 10

−2

5 10 1.680711 ×10

−2

1.496981 × 10

−2

10 2 2.289850 ×10

−1

4.246663 × 10

−2

10 4 1.121958 ×10

−1

2.498364 × 10

−2

10 10 8.999232 ×10

−3

2.819985 × 10

−3

6.5.2.2 Simpliﬁed Models for the Crystal Growth Apparatus: Heat

Equation with Nonlinear Heat Source

In the second test example, we deal with a two-dimensional heat equation

with a nonlinear heat source, see [3].

The two-dimensional heat equation is given as

∂

u(x, y, t)=u

+ u

−4(1 + y

)exp(−t)exp(x + y

), in Ω × [0,T], (6.88)

u(x, y, 0) = exp(x + y

), on Ω, (6.89)

u(x, y, t)=exp(−t)exp(x + y

), on ∂Ω × [0,T], (6.90)

where the domain is Ω = [−1, 1] × [−1, 1] and the end time is T =1.

The exact solution is given as

u(x, y, t)=exp(−t)exp(x + y

). (6.91)

170Decomposition Methods for Diﬀerential Equations Theory and Applications

We choose the time interval [0,1] and again apply the ﬁnite diﬀerences for

space with Δx =Δy =2/19. We use the operator-splitting method for

decomposition. The domain is split into two subdomains.

The operator equation is given as

∂

u(x, y, t)=Au + Bu + f(x, y),

where f (x, y)=−4(1 + y

)exp(−t)exp(x + y

), and the operators are given

Au =

+ u

, for (x, y) ∈ Ω

0, for (x, y) ∈ Ω

, (6.92)

Bu =

0, for (x, y) ∈ Ω

+ u

, for (x, y) ∈ Ω

, (6.93)

with Ω

∪ Ω

=ΩandΩ

∩ Ω

= ∅.

The initial and boundary conditions are given as in Equations (6.88)–(6.90).

We choose the splitting intervals Ω

=[−1, 0] × [−1, 1] and Ω

=[0, 1] ×

[−1, 1].

For the approximation error we apply the maximum norm (L

∞

-norm), given

as err

u,L

∞

=max

i,j

exact

,T) −u

approx

(iΔx, jΔy, T)|,whereT =1.0.

The results of the experiment are presented in Table 6.40. The experiments

are programmed in MATLAB 7.0 and computed with a 2 GHz Linux personal

computer, with computation accuracy of around 10

−313

The maximal error decreases with increasing iteration steps. Further com-

parisons to other methods are shown in [88], and based on these results the

iterative operator-splitting method is more accurate.

Graphically, the solution smooths with more relaxation steps as seen in

Figure 6.18.

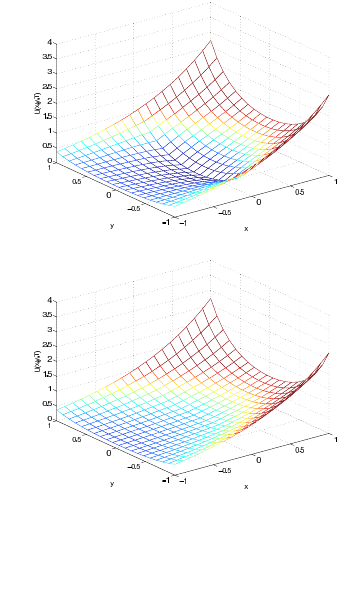
Numerical Experiments 171

FIGURE 6.18: The numerical results of the second example after 10

iterations (left) and 20 iterations (right).

172Decomposition Methods for Diﬀerential Equations Theory and Applications

TABLE 6.40: Numerical results for the

second example with iterative operator-splitting

method and BDF3 method.

Iteration Number of err

u,L

∞

steps splitting partitions

1 1 2.7183e+000

2 1 8.2836e+000

3 1 3.8714e+000

4 1 2.5147e+000

5 1 1.8295e+000

10 1 6.8750e-001

15 1 2.5764e-001

20 1 8.7259e-002

25 1 2.5816e-002

30 1 5.3147e-003

35 1 2.8774e-003

6.5.2.3 Real-Life Problem: Crystal Growth Apparatus

We concentrate on the stationary heat conduction in potentially anisotropic

materials.

We consider the following underlying equation:

−div(K

(θ) ∇θ)=f

, in Ω

,(m ∈ M), (6.94)

where θ ≥ 0 represents the absolute temperature, the symmetric and positive

deﬁnite matrix K

represents the thermal conductivity tensor in the material

m, f

≥ 0 represents the heat sources in the material m due to some heating

mechanism (e.g., induction or resistance heating), Ω

is the domain of the

material m,andM is a ﬁnite index set. We consider the case in which the ther-

mal conductivity tensor is a diagonal matrix with temperature-independent

anisotropy that is,

(θ)=



i,j

(θ)



, where κ

i,j

(θ)



iso

(θ), for i = j

0, for i = j

, (6.95)

iso

(θ) > 0 being the potential temperature-dependent thermal conductivity

of the isotropic case, and α

> 0 being the anisotropy coeﬃcients. As an

example, the growth apparatus used in silicon carbide single crystal growth

by physical vapor transport (PVT) is usually insulated by graphite felt in

which the ﬁbers are aligned in one particular direction, resulting in a thermal

conductivity tensor of the form (6.95). We apply the ﬁnite volume scheme,

based on control volumes, see [96], and consider the anisotropy in the thermal

insulation of the PVT growth apparatus.

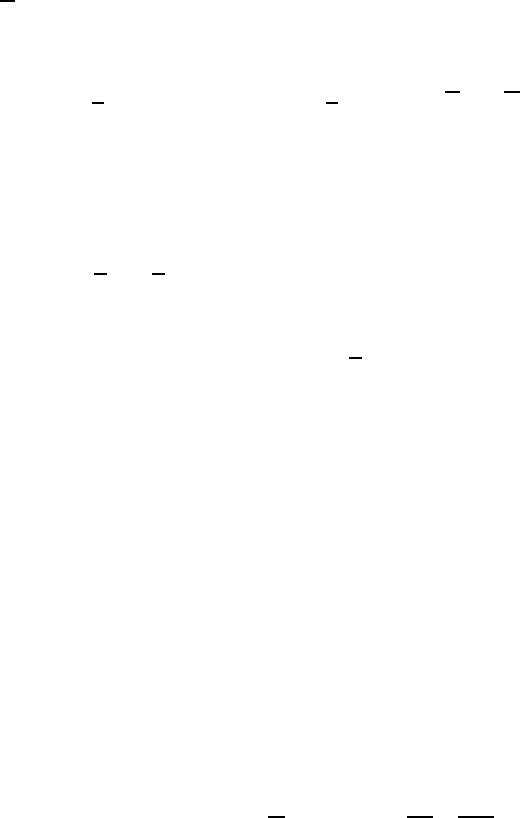
Numerical Experiments 173

The temperature θ is assumed to be continuous throughout the entire do-

main

Ω. The continuity of the normal component of the heat ﬂux on the

interface between diﬀerent materials m

and m

, m

= m

, yields the follow-

ing interface conditions, coupled with the heat equations (6.94):



(θ) ∇θ





·n



(θ) ∇θ





·n

, on Ω

∩ Ω

, (6.96)

where  denotes restriction, and n

denotes the unit normal vector pointing

from material m

to material m

We consider two types of outer boundary conditions, namely Dirichlet and

Robin conditions. To that end, we decompose ∂Ω according to

• Let Γ

Dir

and Γ

Rob

be relatively open polyhedral subsets of ∂Ω, such

that ∂Ω=

Dir

∪ Γ

Rob

,Γ

Dir

∩ Γ

Rob

= ∅.

The boundary conditions are then given as

θ = θ

Dir

, on Γ

Dir

, (6.97a)

−



(θ) ∇θ



· n

= ξ

(θ − θ

ext,m

on Γ

Rob

∩ ∂Ω

, m ∈ M, (6.97b)

where n

is the outer unit normal to Ω

, θ

Dir

≥ 0 is the given temperature

on Γ

Dir

, θ

ext,m

≥ 0 is the given external temperature ambient to Γ

Rob

∩∂Ω

and ξ

> 0 is a transition coeﬃcient.

Our apparatus is given in Figure 6.19.

The radius is 12 cm and the height is 45.3 cm. This domain represents a

growth apparatus used in silicon carbide single crystal growth by the PVT

method. The domain Ω consists of six subdomains Ω

, m ∈{1,...,6},

representing the insulation materials, graphite crucible, SiC crystal seed, gas

enclosure, SiC powder source, and quartz. In order to use realistic functions

for the isotropic parts κ

iso

(θ) of the thermal conductivity tensors (cf. (6.95)),

for gas enclosure, graphite crucible, insulation, and SiC crystal seed, we use

the functions given by (A.1), (A.3b), (A.4b), and (A.7b) in [139]; for κ

iso

(θ)

(SiC powder source), we use [137, (A.1)], and for κ

iso

(θ) (quartz), we use

iso

(θ)=



1.82 − 1.21 · 10

−3

+1.75 · 10

−6



. (6.98)

Hence, all functions κ

iso

(θ) depend nonlinearly on θ. As mentioned in the in-

troduction, the thermal conductivity in the insulation is typically anisotropic

in PVT growth apparatus. In the numerical experiments reported below,

we therefore vary the anisotropy coeﬃcients (α

,α

) of the insulation while

keeping (α

,α

)=(1, 1) for all other materials m ∈{2,...,5}.

Heat sources f

= 0 are supposed to be present only in the part of Ω

(graphite crucible) labeled “uniform heat sources” in the left-hand picture in

Figure 6.20, satisfying 5.4cm≤ r ≤ 6.6cmand9.3cm≤ z ≤ 42.0cm.

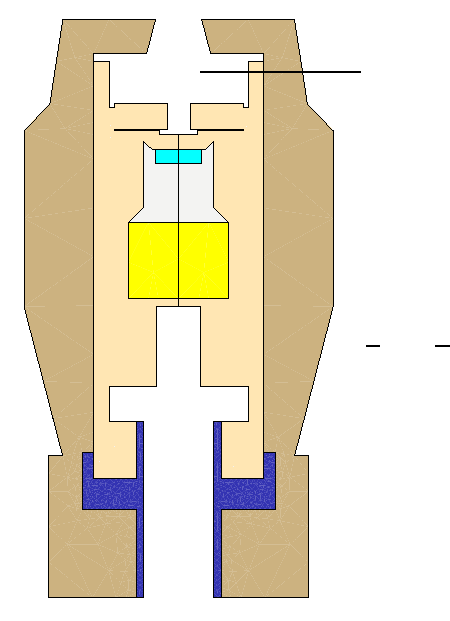
174Decomposition Methods for Diﬀerential Equations Theory and Applications







Blind hole

(for cooling and measurements).

: Insulation (often anisotropic).

: Graphite crucible.

: SiC crystal seed.

: Gas enclosure.

:SiCpowdersource.

:Quartz.

Ω=

m=1

FIGURE 6.19: The underlying apparatus given as an axis-symmetric

domain with the diﬀerent material regions.

In that region, f

is set to be the constant value f

=1.23 MW/m

,which

corresponds to a total heating power of 1.8 KW. This serves as an approxi-

mation to the situation typically found in a radio-frequent induction-heated

apparatus, where a moderate skin eﬀect concentrates the heat sources within

a few millimeters of the conductor’s outer surface.

Here, our main goal is to illustrate the eﬀectiveness of our spatial discretiza-

tion method based on ﬁnite volume schemes. With such results, we can apply

our decomposition methods to separate the anisotropic directions.

This is the case if the anisotropy in the thermal conductivity of the insula-

tion is suﬃciently large. For such a case we expect the isotherms to be almost

parallel to the direction with the larger anisotropy coeﬃcient. Because using

the Dirichlet boundary condition (6.97a) can suppress such an alignment of

the isotherms, we prefer the Robin condition (6.97b) on all of ∂Ω instead. For

m ∈{1, 2, 6},wesetθ

ext,m

= 500 K and ξ

=80W/(m

K).

Numerical Experiments 175

We now present the results of our numerical experiments, varying the

anisotropy coeﬃcients (α

,α

) in the insulation.

In each case, we use a ﬁne grid consisting of 61,222 triangles. We start

with the isotropic case (α

,α

)=(1, 1) depicted on the right-hand side of

Figure 6.20. Figure 6.21 shows the computed temperature ﬁelds for the mod-

erately anisotropic cases (α

,α

)=(10, 1) (left), (α

,α

)=(1, 10) (middle),

(α

,α

)=(10, 1) in top and bottom insulation parts, (α

,α

)=(1, 10) in

insulation side wall (right).

The maximal temperatures established in the four experiments are collected

in Table 6.41.

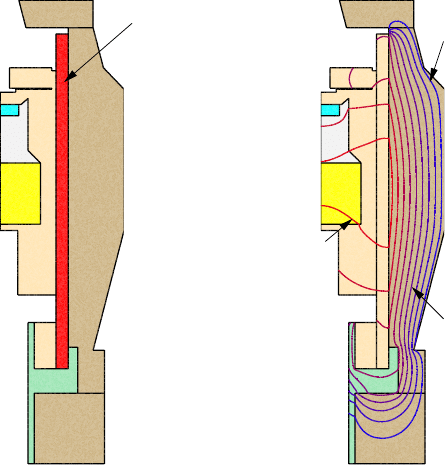
Location of heat sources

uniform heat sources

field

Stationary temperatur

1220 K

580 K

820 K

FIGURE 6.20: Left: Location of the heat sources; Right: Computed tem-

perature ﬁeld for the isotropic case α

= α

= 1, where the isotherms are

spaced at 80 K.

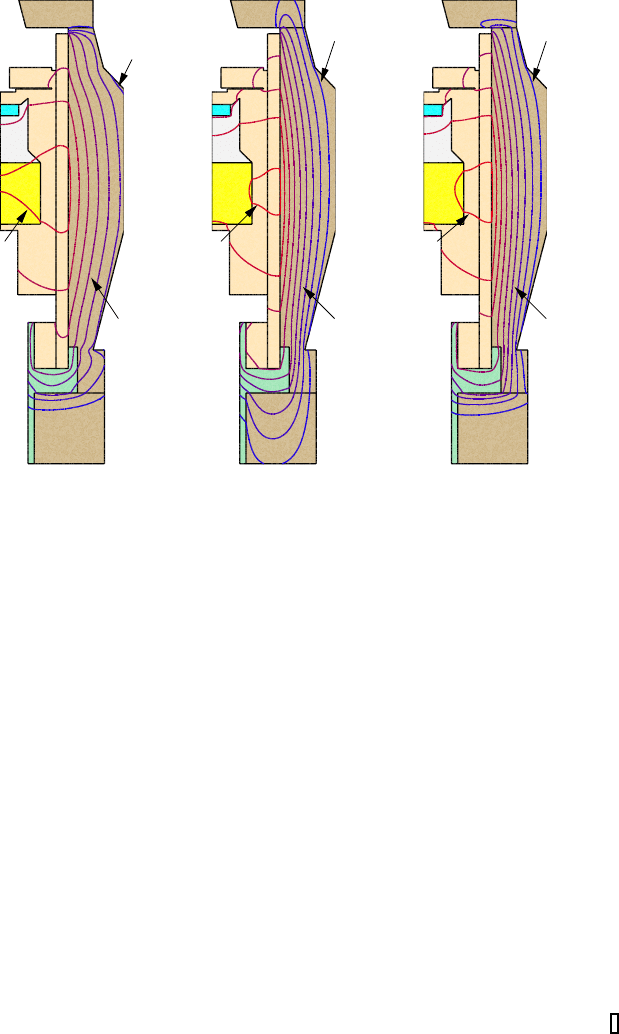
Comparing the temperature ﬁelds in Figures 6.20 and 6.21 and the maximal

temperatures listed in Table 6.41, we ﬁnd that any anisotropy reduces the

eﬀectiveness of the thermal insulation, where a stronger anisotropy results

in less insulation. A stronger anisotropy results in a less eﬀective insulation

and the value above 1 improves the insulation’s thermal conductivity in that

176Decomposition Methods for Diﬀerential Equations Theory and Applications

field

Stationary temperatur

850 K

750 K

550 K

field

Stationary temperatur

1220 K

580 K

800 K

field

Stationary temperatur

1220 K

580 K

800 K

FIGURE 6.21: Computed temperature ﬁelds for the moderately

anisotropic cases (α

,α

)=(10, 1) (left, isotherms spaced at 50 K); (α

,α

(1, 10) (middle, isotherms spaced at 80 K); (α

,α

)=(10, 1) in top and bot-

tom insulation parts, (α

,α

)=(1, 10) in insulation side wall (right, isotherms

spaced at 80 K).

direction. Similarly, when reducing one of the anisotropy coeﬃcients to a

value below 1, a stronger anisotropy would result in improved insulation.

The application of decoupling methods to this real-life application is very

important because of its complicated domains with diﬀerent parameters. Each

simpler domain can be computed more accurately and parallel computation

is possible. In this version, only the test examples are performed with the

decomposition methods.

REMARK 6.16 The underlying real-life application can be computed

more eﬃciently with spatial decomposition methods. In further experiments,

we will show that spatial decomposition methods are more adaptive to the

underlying domains and can beneﬁt from parallelization.