Geiser J. Decomposition Methods for Differential Equations: Theory and Applications

Подождите немного. Документ загружается.

Numerical Experiments 187

FIGURE 6.25: Contour plot of the y-component on a plane for the 3D

case with a singular force. The inclusion of an isosurface for ||U|| is also done.

A vital component of a model in seismology is the stable higher-order ap-

proximation of the boundary conditions, something we have saved for a future

manuscript.

6.5.4 Magnetic Layers

The motivation for the study is coming from modeling ferromagnetic mate-

rials, used in data storage devices and laptop displays. The models are based

on the Landau-Lifschitz-Gilbert equation, see [144], and are extended by the

interaction of diﬀerent magnetic layers. The application of such model prob-

lems include switch processes in magnetic transistors (FET) or data devices.

Mathematically the equations cannot be solved analytically and numerical

methods are important. Therefore, numerical methods for stable discretiza-

tions are important because of the known blow-up eﬀects, see [19] and [174].

We apply the scalar theory and present the extention to more complicated sys-

tems of magnetic models. In the numerical examples we present ﬁrst results

of single layers and inﬂuence with external magnetic ﬁelds.

6.5.4.1 Discretization and Solver Methods

For the discretization method we apply a stable implicit method. In general

the equations are iteratively solved with semi-discretization. We obtain a

188Decomposition Methods for Diﬀerential Equations Theory and Applications

general discretized equation given as

∂

= A

+ B

+ H

eff,1

i−1

) , (6.114)

∂

i+1

= A

i+1

+ B

i+1

+ H

eff,2

i+1

) , (6.115)

where i =0, 1, 2,....

In the following we discuss the scalar and the system cases.

6.5.4.2 Implicit Discretization for Scalar LLG Equations

We apply the following discretization :

⊂ W

1,2

(Ω, R

), T

a triangulation, m

∈ V

, m

∈ V

The full discretization is given with a linearization :

(∂

j+1

,φ

)

+ α(m

× ∂

j+1

,φ

)

(6.116)

=(1+α

)(m

j+1/2

× Δ

j+1/2

,φ

)

where φ

∈ V

and j : index for the time-steps.

∂m

j+1

= k

−1

j+1

− m

)andk = t

j+1

− t

j+1/2

=1/2(m

j+1

+ m

)

Further the constraint : |m

| = 1 discrete energy law.

We deal with the anisotropic model and add the magnetic ﬁeld H

eff

In the weak formulation, we can formulate

(∂

m, φ)+α(m × ∂

m, φ)=(1+α

)(m × Δm, φ) (6.117)

+(1 + α

)(m × H

eff

,φ) ,

with the initial condition m(0) = m

∈ W

1,2

(Ω; S

) and the magnetic ﬁeld is

given as H

eff

The full discretization is given with a linearization:

(∂

j+1

,φ

)

+ α(m

× ∂

j+1

,φ

)

(6.118)

=(1+α

)(m

j+1/2

× (Δ

j+1/2

+ H

eff

j+1/2

),φ

)

where φ

∈ V

and j : index for the time-steps.

6.5.4.3 Stability Theory for the LLG Equation

In the previous work of [19] the problems of higher-order derivatives are

discussed.

We will concentrate on the nonlinear case H(u) and time-dependent case

H(t).

For both we could derive a stabile implicit discretization method. In the

following we present the ﬁxpoint-algorithm to solve Equation (6.118).

ALGORITHM 6.1

Set m

j+1,l

:= m

and l := 0.

Numerical Experiments 189

(i) Compute m

j+1,l+1

∈ V

such that for all φ

∈ V

there holds

1/k(m

j+1,l+1

,φ

)

+ α/k(m

× m

j+1,l+1

,φ

)

(6.119)

−(1 + α

)/4(m

j+1,l+1

× (Δ

j+1,l

+ H

j+1

eff

),φ

)

−(1 + α

)/4(m

× (Δ

j+1,l

+ H

j+1

eff

),φ

)

−(1 + α

)/4(m

× (Δ

j+1,l+1

+ H

j+1

eff

),φ

)

=1/k(m

,φ

)

+(1+α

)/4(m

× (Δ

+ H

eff

),φ

)

(ii) If ||m

j+1,l+1

− m

j+1,l

≤  then stop and set m

j+1

:= m

j+1,l+1

(iii) Set l := l +1 and go to (i).

We can derive the error estimates.

LEMMA 6.1

Suppose that we have γ dependent from h, k,andα,and|m

)| =1for

all m. Then for all l ≥ 1 there holds

||m

j+1,l+1

− m

l+1,l

≤ Θγ||m

j+1,l

− m

l+1,l−1

. (6.120)

PROOF

The proofs follow the paper of [19].

REMARK 6.19 For the ﬁx-point problem, we can stabilize our scheme

by the linearization of the last solutions. With more iterations, the stabiliza-

tion is obtained. Here is also a balance between the time partitions and the

iterations important to save computational time.

In the next section our numerical examples are based on the magnetization

of isotropic and anisotropic materials.

The isotropic material on the one hand is hard to control, where the anisotropic

material has special directions to follow by the discretization.

6.5.4.4 Test Example of the LLG Equation with Pure Isotropic

Case

We start with a ﬁrst example to use the stabile ﬁrst-order splitting as a

prestep method. In the test example for the pure isotropic case, we have a

190Decomposition Methods for Diﬀerential Equations Theory and Applications

situation, without an inﬂuence by an outer magnetic ﬁeld:

= u × Δu − λu × (u × Δu), (6.121)

where λ =1,Ω=[-0.5, 0.5]

We concentrate on diﬀerent initial values that complicate the computations

1. Case

(2xA; A

−|x|

)/(A

+ |x|

)for|x| < 0.5

(0; 0; −1) for |x| > 0.5

(6.122)

2. Case

(2xA; A

−|x|

)/(A

+ |x|

)for|x| < 0.05

(0; 0; −1) for |x| > 0.05

(6.123)

3. Case

=[2xA; A

−|x|

]/(A

+ |x|

)forx ∈ Ω (6.124)

where A =(1−2|x|)

/4.

The convergence-results are given in Tables 6.46 and 6.47:

TABLE 6.46: Relative errors between l =4and

l =6.

x y L

(relative error) L

∞

(relative error)

0 0 0.487524 1.999790

−1 0 0.201978 0.426290

0 −1 0.199584 0.426297

1 0 0.198766 0.426282

0 1 0.201194 0.426287

The results show the switching of the singular point in more unstable situ-

ations as the nonsingular points.

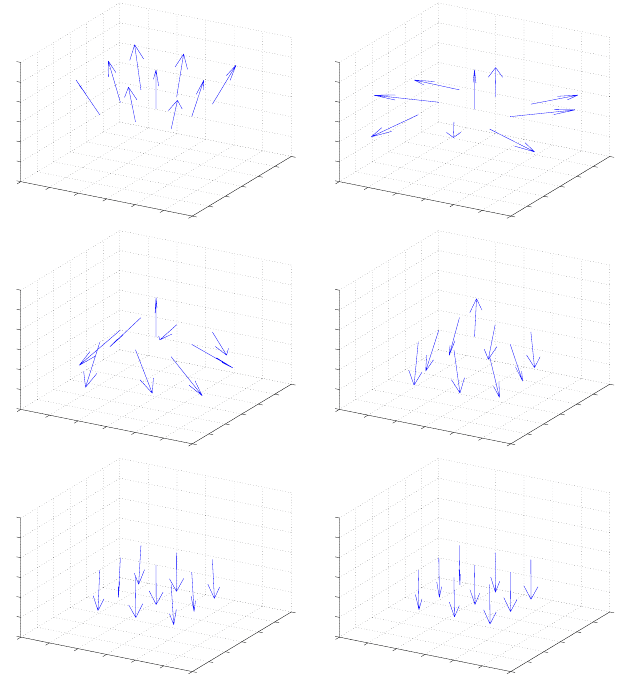
The computational results of the singular point are presented in Figure

6.26.

The inﬂuence of the external ﬁeld is presented in Figure 6.27.

In a next experiment one can present a more stable conﬁguration with an

external ﬁeld.

Numerical Experiments 191

0 500

000

500

000

500 3000 3500

000

500

0 8

0 6

0 4

0 2

0 4

0 6

0 8

0 500 1000 1500 2000 2500 3000 3500 4000 4500

0 8

0 6

0 4

0 2

0 4

0 6

0 8

FIGURE 6.26: Left: Magnetization on the point (0, 0), right: magnetiza-

tion on the point (1, 0) with the coordinates: red = x, green = y,blue=

192Decomposition Methods for Diﬀerential Equations Theory and Applications

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

0 1

0 05

0 1

0 15

FIGURE 6.27: Figures top-down and left-right present time-sequence of a

magnetic layer in a pure isotropic case.

Numerical Experiments 193

TABLE 6.47: Relative errors between l =5and

l =6.

x y L

(relative error) L

∞

(relative error)

0 0 0.662921 1.999939

−1 0 0.191115 0.453568

0 −1 0.194658 0.468610

1 0 0.198813 0.493772

0 1 0.195291 0.479565

6.5.4.5 Test example of the LLG Equation with External Field

eff

(t)

The following problem is discussed as magnetization based with an external

magnetic ﬁeld.

= u × (Δu + H

eff

) − λu × (u × (Δu + H

eff

)), (6.125)

where λ =1,Ω=[-0.5, 0.5]

,andα =1,H

ext

=(1, 0, 40) (e.g., with a strong

right-hand side inﬂuence).

We concentrate on diﬀerent initial values that are given as

(2xA; A

−|x|

)/(A

+ |x|

)for|x| < 0.5

(0; 0; −1) for |x| > 0.5

. (6.126)

The spatial discretization is done with 9 × 9 points in the domain, and the

time discretization is based on a time-step Δt =1/640.

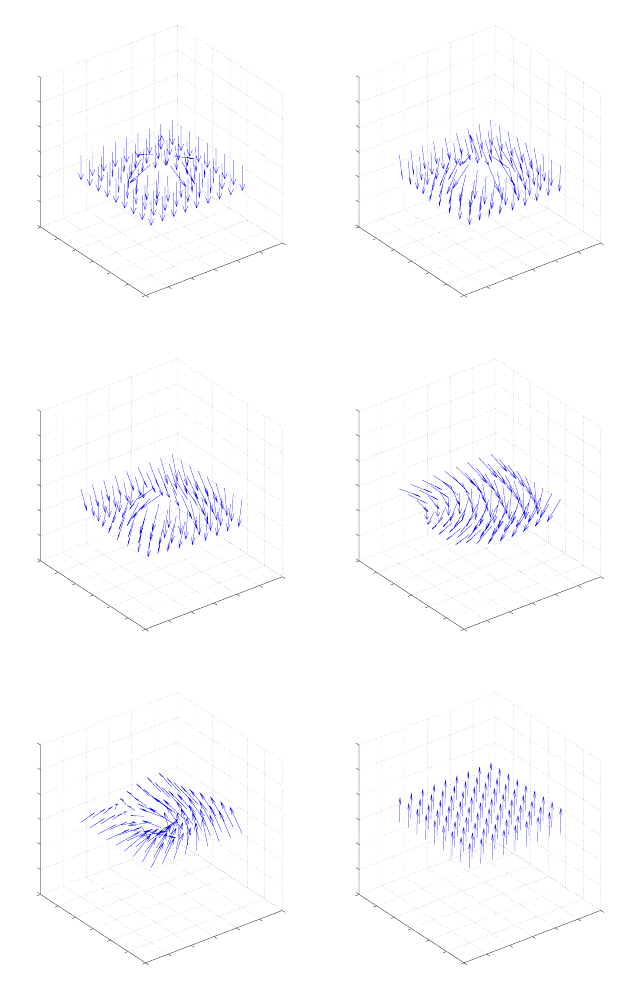
In Figure 6.28 we present the inﬂuence of the external ﬁeld.

The interaction between the particles is very strong with the help of the

ext

. The internal vector has a rapid change, due to the symmetry break (i.e.,

with H

ext

). In the next time-steps the magnetization vectors are oriented to

the external ﬁeld (i.e., to the top of the material).

REMARK 6.20

We present the combination with isotropic and anisotropic magnetization

behavior. Stable discretization methods based on penalizing methods are

described, further splitting methods could decouple the complicated equa-

tions. In numerical experiments we verify our theoretical results. In the future

the nonsmooth treatment of magnetic ﬁelds with comparison of experimental

dates is proposed.

194Decomposition Methods for Diﬀerential Equations Theory and Applications

FIGURE 6.28: Figures top-down and left-right present time-sequence of a

magnetic layer inﬂuenced by an external magnetic ﬁeld H

xt =(1, 0, 40).

Chapter 7

Summary and Perspectives

The monograph presented splitting analysis for evolution equations. In several

chapters, both time and space scales are treated and balanced to achieve

accurate and stable methods.

The numerical analysis for the iterative operator-splitting methods is pre-

sented to quasi-linear, stiﬀ, spatiotemporal problems. Further, we discuss the

applications to hyperbolic equations, with respect to systems of wave equa-

tions.

The following contributions are treated:

• Generalization of consistency and stability results to nonlinear, stiﬀ and

spatial decomposed splitting problems

• Acceleration of the computations by decoupling into simpler problems

• Eﬃciency of the decomposed methods

• Theory based on semigroup analysis which is well understood and ap-

plicable to the splitting methods

• Applications in computational sciences (e.g., ﬂow problems, elastic wave

propagation, heat transfer).

Based on the iterative splitting methods, the important ﬁx-point problem,

with respect to the initial solutions or starting solutions, is important.

So the following items should be further discussed and developed in

algorithms:

• Improved starting solution for the ﬁrst iterative step by solving the ﬁx-

point problem accurate (e.g., embedded Newton-solver)

• Parallelization of the iterative methods on the operator level

• Decoupling algorithms with respect to the spectrum of the operators

and atomization the decomposition process

• Simulation of real-life problems with improved parallel splitting

methods

195

196Decomposition Methods for Diﬀerential Equations Theory and Applications

The perspective for the decomposition methods is combing the eﬃciency

decoupling and generalization due to nonlinear and boundary problems. The

decomposition methods are adaptive methods that respect the physical con-

servation of the equation and accelerate the solving process of a complicated

system of coupled evolution equations.