Geiser J. Decomposition Methods for Differential Equations: Theory and Applications

Подождите немного. Документ загружается.

218Decomposition Methods for Diﬀerential Equations Theory and Applications

Errors at time T: L1-error = 0.0038664, max. error = 0.0096016

The L

X-code for the table and the plots, see Table A.1 and Figure A.3,

is given as well.

TABLE A.1: Numerical results for wave equation with

coeﬃcients (D

)=(1, 1) using etaIOS method, initial condition

n+1,0

(t)=U

, and two iterations per time-step.

Δx =Δy Δt err

err

max

0.25 0.3125 0.048967 0.13442

0.125 0.3125 0.021581 0.054647 1.1821 1.2985

0.0625 0.3125 0.014382 0.035715 0.58548 0.61361

0.25 0.15625 0.042097 0.11556

0.125 0.15625 0.014849 0.037601 1.5034 1.6199

0.0625 0.15625 0.0077193 0.01917 0.94382 0.97195

0.25 0.078125 0.038395 0.1054

0.125 0.078125 0.011013 0.027888 1.8017 1.9182

0.0625 0.078125 0.0038664 0.0096016 1.5102 1.5383

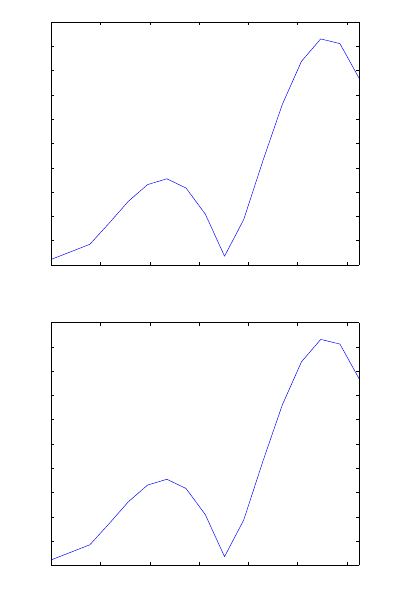
Software Tools 219

0 0.2 0.4 0.6 0.8 1 1.2

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

0.045

0.05

Error for wave equation for t∈[0,1.25] with Δ x=0.25

0 0.2 0.4 0.6 0.8 1 1.2

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

0.045

0.05

Error for wave equation for t∈[0,1.25] with Δ x=0.25

FIGURE A.3: Two of the ﬁgures that are automatically created by

FIDOS.

Appendix B

Discretization Methods

In this appendix, we discuss the spatial and time discretization methods that

we applied in our previous chapters.

B.1 Discretization

In the discretization we deal with the underlying methods to obtain a system

of ordinary diﬀerential equations.

The underlying idea is to use the spatial discretization methods to transform

our partial diﬀerential equations into ordinary diﬀerential equations. The

resulting operator equations can be treated with the decomposition methods

and the theory is based on the semigroup analysis.

We concentrate on the Galerkin method to do the spatial discretization.

B.1.1 Galerkin Method

The underlying ideas of transforming the spatial diﬀerential terms into op-

erators are given in the Galerkin method.

The method we obtain approximates the Galerkin solutions and reaches

an operator equation that can be treated as a system of ordinary diﬀerential

equations.

We have the following method:

• Multiplication of the diﬀerential equation for u by the functions v ∈ K

and integration over Ω with subsequent integration by parts yields to

the generalized problem.

• The function class K has to be chosen in such a way that a suﬃcient

smooth solution u of the generalized problem is also a solution of the

original classical problem in the case where the data are suﬃciently

smooth (boundary, coeﬃcients, boundary and initial value, etc.).

• Restriction to u and v in the generalized problem to appropriate ﬁnite-

dimensional subspaces.

221

222Decomposition Methods for Diﬀerential Equations Theory and Applications

The classical derivatives are replaced by generalized (weak) derivatives. The

realization of the Galerkin method is done with the basis functions w

,...,w

see [200].

In the following, we realize the abstract ideas to the parabolic and hyper-

bolic diﬀerential equations, where the aim is to derive the operator equation.

With this abstract generalized problem of coupled systems, we can apply the

splitting methods.

B.1.2 Parabolic Diﬀerential Equation Applied with the Galerkin

Method

In the following we apply the Galerkin method to a parabolic diﬀerential

equation given as

(x, t) − Δu(x, t)=f(x, t) , in Ω × [t

,T] , (B.1)

u(x, t)=0, on ∂Ω × [t

,T] (boundary condition) ,

u(x, 0) = u

(x) , on Ω (initial condition).

The generalized problem of Equation (B.1) yields to the following formulation:

We seek a function u ∈ C([t

,T]; L

(Ω)) ∩ C((t

,T]; H

(Ω)), such that



u(x, t)v(x) dx







i=1

u(x) D

v(x) − fv(x)



dx =0, (B.2)

u(x, t)=0, on ∂Ω × [t

,T] (boundary condition),

u(x, 0) = u

(x) , on Ω (initial condition),

holds for all v ∈ C

∞

(Ω)∩H

(Ω). Further, we assume f(x, t) ∈ L

([t

,T]; L

(Ω))

and u

(x) ∈ H

(Ω).

The function v only depends on the space variable x.

In order to construct an approximate solution u

with the Galerkin method,

we make the following attempt:

(x, t)=



k=1

k,m

(t) w

(x) , (B.3)

where the unknown coeﬃcient c

k,n

depends on time, and we replace u in

the generalized problem (B.2) by u

and require that (B.2) holds for all v ∈

span{w

,...,w

}. Then we obtain the Galerkin equations for j =1,...,m:



k=1



(t)





k=1





i=1

dx =



dx , (B.4)

Discretization Methods 223

where we have a linear system of ﬁrst-order ordinary diﬀerential equations for

the real functions c

,...,c

. n is the number of the dimension for the test

space, and for m →∞we obtain the convergence of u

to u.

Based on this notation we can write in abstract operator equations:



(t)+Ac

(t)=F (t) , in [t

,T], (B.5)

(0) = α

, (B.6)

where

M =

⎛

⎜

⎝



dx ...



dx ...



⎞

⎟

⎠

, (B.7)

A =

⎛

⎜

⎝





i=1

dx ...





i=1





i=1

dx ...





i=1

⎞

⎟

⎠

, (B.8)

and F(t)=(



dx,...,



dx)

are the operators.

The initial conditions c

(0) correspond to the approximately initial condi-

tion of the original problem, so we choose a sequence

m,0

(x)=



k=1

(x), (B.9)

where u

m,0

converges to u

as m →∞.

For the boundary conditions we have also

m,0

(x, t)=0, on ∂Ω × [t

,T]. (B.10)

REMARK B.1 If we replace the linear operators by nonlinear opera-

tors in (B.1), we obtain a nonlinear system of ordinary diﬀerential equations.

This can be treated by linearization and we obtain again our linear ordinary

diﬀerential equations.

REMARK B.2 The extensions with convection and reaction terms

can also be done with the presented parabolic diﬀerential equation. The

generalization is done in [81] and [124]. Because of the operator notation

as a further simpliﬁcation of the presented partial diﬀerential equations, we

concentrate on the diﬀusion term.

224Decomposition Methods for Diﬀerential Equations Theory and Applications

B.1.3 Hyperbolic Diﬀerential Equation Applied with the Galerkin

Method

In the following, we apply the Galerkin method to a hyperbolic diﬀerential

equation given as:

(x, t) − Δu(x, t)=f(x, t) , in Ω × [t

,T] , (B.11)

u(x, t)=0, on ∂Ω × [t

,T] (boundary condition),

u(x, 0) = u

(x) , on Ω (initial condition),

(x, 0) = u

(x) , on Ω,

where f,u

are given and we seek u.

The generalized problem of Equation (B.11) yields to the following

formulation:

We seek a function u(x, t) ∈ C

([t

,T]; L

(Ω))∩C([t

,T]; H

(Ω)), such that



u(x, t)v(x) dx







i=1

u(x, t) D

v(x) − f(x, t) v(x)



dx =0, (B.12)

u(x, t)=0, on ∂Ω × [t

,T] (boundary condition),

u(x, 0) = u

(x) on Ω (initial condition),

(x, 0) = u

(x) on Ω (initial condition),

holds for all v(x) ∈ C

∞

(Ω) ∩ H

(Ω).

Further, we assume f(x, t) ∈ L

([t

,T]; L

(Ω)), u

(x) ∈ H

(Ω), and u

(x) ∈

(Ω).

The function v(x) depends only on the spatial variable x.

In order to construct an approximate solution u

with the Galerkin method,

we make the following attempt:

(x, t)=



k=1

k,m

(t) w

(x) , (B.13)

where the unknown coeﬃcient c

k,m

depends on time, and we replace u in the

generalized problem (B.12) by u

and require that (B.12) holds for all v ∈

span{w

,...,w

}. Then we obtain the Galerkin equations for j =1,...,m:



k=1



(t)









i=1

dx =



dx , (B.14)

Discretization Methods 225

where we have a linear system of second-order ordinary diﬀerential equations

for the real functions c

,...,c

Based on this notation we can write in abstract operator equations:



(t)+Ac

(t)=F (t) , in [t

,T], (B.15)

(0) = α

, (B.16)



(0) = β

, (B.17)

where M and A are given as in Equations (B.7) and (B.8).

The initial conditions c

(0) and c



(0) correspond to the approximately initial

condition of the original problem, so we choose a sequence

m,0

(x)=



k=1

(x), (B.18)

m,1

(x)=



k=1

(x), (B.19)

where u

m,0

converges to u

and u

m,1

to u

as m →∞.

For the boundary conditions, we also have

m,0

(x, t)=0, on ∂Ω × [t

,T] . (B.20)

REMARK B.3 If we replace the linear operators by nonlinear opera-

tors in (B.11), we obtain a nonlinear system of ordinary diﬀerential equations.

This can be treated by linearization (e.g., Newton method or ﬁxpoint itera-

tions, see [131]), and we obtain again our linear ordinary diﬀerential equations.

B.1.4 Operator Equation

For more abstract treatment of our splitting methods in Chapter 3, we deal

in the following with the operator equations:

(u(t),t)+A

(u(t),t)+B(u(t),t)=0, ∀t ∈ [t

,T], (B.21)

where A

,B,C

are positive deﬁnite and symmetric operators, so at

least also boundable operators for all t ∈ [t

,T].

We have also reset the notation c

to u for the abstract treatment. At least

the results have to be retransformed with the test-space, see Equation (B.13).

For the operator equations we can in the following chapters treat our un-

derlying splitting methods with the semigroup theory.

226Decomposition Methods for Diﬀerential Equations Theory and Applications

B.1.5 Semigroup Theory

With the notion of a semigroup we can describe time-dependent processes

in nature in terms of the functional analysis. We describe an introduction

that is needed in the further sections. An overview to the semigroup theory

can be found in [12], [13], [65], [191], [198], [200], and [201].

The key relations are

S(t + s)=S(t)S(s) , ∀t, s ∈ R

, (B.22)

S(0) = I, (B.23)

and we have the following deﬁnition of a generator of a semigroup.

DEFINITION B.1 Asemigroup{S(t)} on a Banach space X consists

of a family of operators S(t):X → X for all t ∈ R

with B.22 and B.23. The

generator B : D(B) ⊂ X → X of the semigroup {S(t)} is deﬁned by

Bw = lim

t→0

S(t)w − w

, (B.24)

where w belongs to D(B), if the limit of B.24 exists.

A one-parameter group {S(t)} on the Banach space X consists of a family

of operators S(t):X → X for all t ∈ R, with (B.22) for all t, s ∈ R and (B.23)

as the initial condition.

REMARK B.4 A family {S(t)} of linear continuous operators from

X to itself, which satisﬁes the conditions with (B.22) and (B.23), is called a

continuous semigroup of linear operators or simply a C

semigroup.

B.1.6 Classiﬁcation of Semigroups

Let S = {S(t)} be a semigroup of the Banach space X.

We have the following classiﬁcation of the semigroups:

1. S is called strongly continuous, if t → S(t)w is continuous on R

for all

w ∈ X that is,

lim

t→s

S(t)w = S(s)w, ∀s ∈ R

. (B.25)

2. S is called uniformly continuous, if all operators S(t):X → X are linear

and continuous, and t → S(t) is continuous on R

with respect to the

operator norm that is,

lim

t→s

||S(t) − S(s)|| =0, ∀s ∈ R

. (B.26)

Discretization Methods 227

3. S is called nonexpansive, if all operators S(t):X → X are nonexpansive

and

lim

t→0

S(t)w = w, ∀w ∈ X. (B.27)

4. S is called a linear semigroup, if all operators S(t):X → X are linear

and continuous.

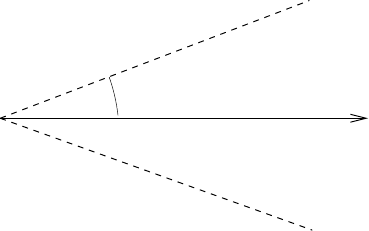
5. S is called an analytical semigroup, if we have an open sector Σ and a

family of linear continuous operators S(t):X → X for all t ∈ Σwith

S(0) = I and the following properties:

(a) t → S(t) is an analytical map from Σ into L(X, Y ),

(b) S(t + s)=S(t)S(s) for all t, s ∈ Σ,

t→0

S(t)w = w in Σ for all w ∈ X,

where an open sector is deﬁned as

Σ={z ∈ C : −α<arg(z) <α, z=0}, (B.28)