Geiser J. Decomposition Methods for Differential Equations: Theory and Applications

Подождите немного. Документ загружается.

Numerical Experiments 147

The noniterative splitting method in the time discretized form is given as

˜u − 2u

+ u

n−1

= τ



∂

˜u

∂x

+(1− 2η)

∂

∂x

+ η

∂

n−1

∂x



(6.48)

+ τ

∂

∂y

n+1

− 2u

+ u

n−1

= τ



∂

˜u

∂x

+(1− 2η)

∂

∂x

+ η

∂

n−1

∂x



(6.49)

+ τ



∂

n+1

∂y

+(1−2η)

∂

∂y

+ η

∂

n−1

∂y



where τ

= t

n+1

−t

is the time-step and the time discretization is of second

order.

6.4.1.1 First Test Example: Wave Equation with Constant

Coeﬃcients

The application of the diﬀerent boundary conditions is important for the

splitting method used for the test example.

Dirichlet Boundary Condition

Our example is two-dimensional, where we can derive an analytical solution:

∂

u = D

∂

u + D

∂

u, in Ω × [0,T] , (6.50)

u(x, y, 0) = u

exact

(x, y, 0), on Ω,

∂

u(x, y, 0) = 0, on Ω,

u(x, y, t)=u

exact

(x, y, t), on ∂Ω × (0,T), (6.51)

where Ω = [0, 1] × [0, 1], D

=1,D

=0.5.

The analytical solution is given as

exact

(x, y, t)=sin(

√

πx)sin(

√

πy)cos(

√

2 πt). (6.52)

The discretization is given with the implicit time discretization and the

ﬁnite diﬀerence method for the space discretization.

Thus, we have for the second-order discretization in space

Au(t)=D

∂

u(t)

≈ D

u(x +Δx, y, t) − 2u(x, y, t)+u(x − Δx, y, t)

Δx

, (6.53)

Bu(t)=D

∂

u(t)

≈ D

u(x, y +Δy, t) −2u(x, y, t)+u(x, y − Δy, t)

Δy

, (6.54)

148Decomposition Methods for Diﬀerential Equations Theory and Applications

and the second-order time discretization

∂

u(t

) ≈

u(t

+ τ

) − 2u(t

)+u(t

− τ

)

. (6.55)

The implicit discretization is

u(t

n+1

) − 2u(t

)+u(t

n−1

) (6.56)

= τ

(A + B)(ηu(t

n+1

)+(1− 2η)u(t

)+ηu(t

n−1

)).

For the approximation error, we choose the L

-norm, also the L

-andL

∞

norm are possible.

The error in the L

-norm is given as

err



i,j=1,...,m

i,j

|u(x

) − u

exact

)|, (6.57)

where u(x

) is the numerical and u

exact

) is the analytical so-

lution. V

i,j

=Δx Δy is the mass, with Δx and Δy the equidistant grid steps

in the x-andy-dimensions. m is the number of the grid nodes in the x-and

y-dimensions.

In our test example we choose D

= D

= 1 (the Dirichlet boundary) and

set our model domain to be a rectangle Ω = [0, 1] × [0, 1].

We discretize with Δx =1/16, Δy =1/16, and τ

=1/32, and choose our

parameter η between 0 ≤ η ≤ 0.5.

The experimental results of the ﬁnite diﬀerences, the classical operator-

splitting method, and the LOD method are shown in Tables 6.21, 6.22, and

6.23 and Figure 6.10.

TABLE 6.21: Numerical

results for ﬁnite diﬀerences method

(second-order ﬁnite diﬀerences in

time and space) and a Dirichlet

boundary.

η err

exact

num

0.0 0.0014 −0.2663 −0.2697

0.1 0.0030 −0.2663 −0.2738

0.3 0.0063 −0.2663 −0.2820

0.5 0.0096 −0.2663 −0.2901

REMARK 6.8 In these experiments, we compare the three diﬀerent

methods based on the ADI method. The splitting methods have the same

Numerical Experiments 149

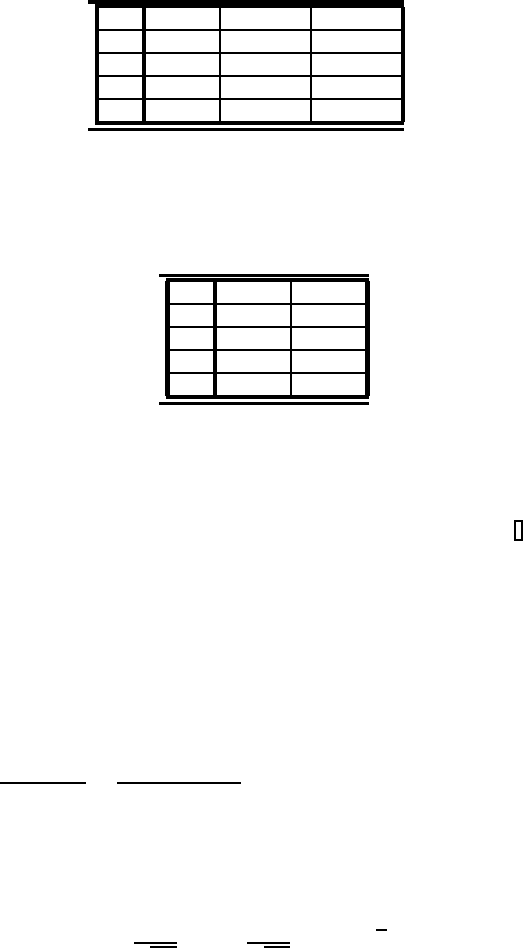
TABLE 6.22: Numerical

results for classical

operator-splitting method

(second-order ADI method) and a

Dirichlet boundary.

η err

exact

num

0.0 0.0014 −0.2663 −0.2697

0.1 0.0030 −0.2663 −0.2738

0.3 0.0063 −0.2663 −0.2820

0.5 0.0096 −0.2663 −0.2901

TABLE 6.23:

Numerical results for

LOD method and a

Dirichlet boundary.

η err

err

∞

0.0 0.0014 0.0034

0.1 0.0031 0.0077

0.3 0.0065 0.0161

0.5 0.0099 0.0245

error reduction quality, while the most accurate method is the LOD method,

which is a fourth-order method. The splitting methods are more eﬀective

methods.

Neumann Boundary Condition

Our next example is two-dimensional, as we saw in the ﬁrst example, but

with respect to the Neumann boundary conditions:

∂

u = D

∂

u + D

∂

u, in Ω × (0,T), (6.58)

u(x, y, 0) = u

exact

(x, y, 0), on Ω,

∂

u(x, y, 0) = 0, on Ω,

∂u(x, y, t)

∂n

∂u

exact

(x, y, t)

∂n

, on ∂Ω × (0,T), (6.59)

where Ω = [0, 1] × [0, 1], D

=1,D

=0.5, and we have an equidistant

time-step τ

The analytical solution is given as

exact

(x, y, t)=sin(

√

πx)sin(

√

πy)cos(

√

2 πt). (6.60)

150Decomposition Methods for Diﬀerential Equations Theory and Applications

0.2

0.4

0.6

0.8

0.5

−1

−0.5

0.5

numeric solution dx=1/32 dy=1/32 dt=1/64 eta=0.5

0.2

0.4

0.6

0.8

0.5

−2

x 10

analytic − numeric dx=1/32 dy=1/32 dt=1/64 eta=0.5

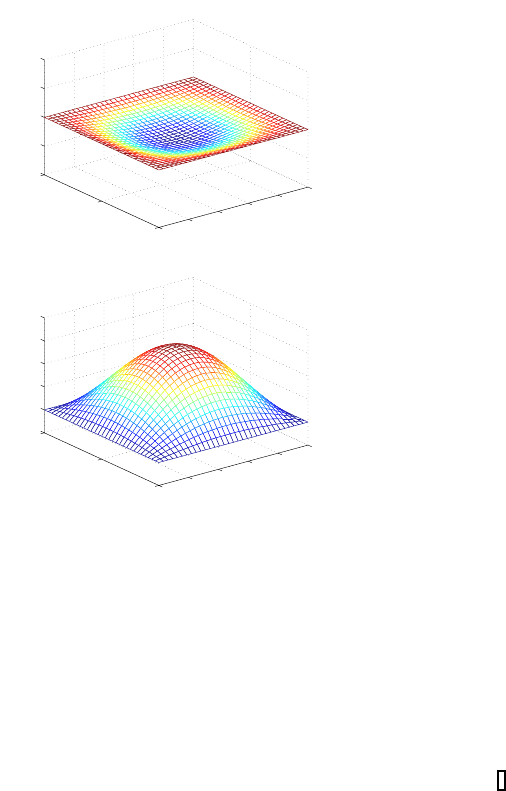
FIGURE 6.10: Numerical resolution of the wave equation: the numerical

approximation (left ﬁgure) and error functions (right ﬁgure) for the Dirichlet

boundary (Δx =Δy =1/32, τ

=1/64, D

=1,D

= 1, coupled version).

The experimental results of the ﬁnite diﬀerences method and classical operator-

splitting method are shown in Tables 6.24, 6.25 and Figure 6.11.

REMARK 6.9 The Neumann boundary conditions are more delicate

because of the underlying boundary splitting methods.

6.4.1.2 Second Test Example: Spatial Dependent Test Example

In this experiment, we apply our method to the spatial dependent problem,

given by

∂

u = D

(x, y)∂

u + D

(x, y)∂

u, in Ω × (0,T), (6.61)

u(x, y, 0) = u

(x, y), in Ω,

∂

u(x, y, 0) = u

(x, y), in Ω,

u(x, y, t)=u

(x, y, t), on ∂Ω × (0,T),

where D

(x, y)=0.1x +0.01y +0.01, D

(x, y)=0.01x +0.1y +0.1.

Numerical Experiments 151

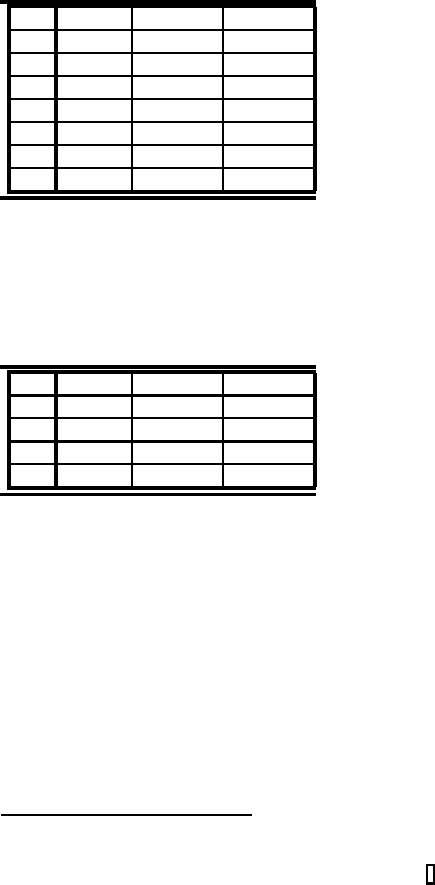
TABLE 6.24: Numerical

results for ﬁnite diﬀerences method

(ﬁnite diﬀerences in time and space

of second order) and a Neumann

boundary.

η err

exact

num

0.0 0.0014 −0.2663 −0.2697

0.1 0.0030 −0.2663 −0.2738

0.3 0.0063 −0.2663 −0.2820

0.5 0.0096 −0.2663 −0.2901

0.7 0.0128 −0.2663 −0.2981

0.9 0.0160 −0.2663 −0.3060

1.0 0.0176 −0.2663 −0.3100

TABLE 6.25: Numerical

results for classical

operator-splitting method (ADI

method of second order) and a

Neumann boundary.

η err

exact

num

0.0 0.0014 −0.2663 −0.2697

0.1 0.0030 −0.2663 −0.2738

0.3 0.0063 −0.2663 −0.2820

0.5 0.0096 −0.2663 −0.2901

To compare the numerical results, we cannot use an analytical solution,

which is why we compute a reference solution in an initial prestep. The

reference solution is performed with the ﬁnite diﬀerence scheme, with ﬁne

time- and space-steps.

When choosing the time-steps, it is important to consider the CFL condi-

tion, which in this case is based on the spatial coeﬃcients.

REMARK 6.10 We have assumed the following CFL condition:

< 0.5

min(Δx, Δy)

max

x,y∈Ω

(x, y),D

(x, y))

, (6.62)

where Δx and Δy are equidistant spatial steps for the x-andy-dimensions.

For the test example, we deﬁne our model domain as a rectangle Ω =

[0, 1] × [0, 1].

152Decomposition Methods for Diﬀerential Equations Theory and Applications

0.5

0.2

0.4

0.6

0.8

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

numeric solution dx=1/32 dy=1/32 dt=1/64 eta=0

0 2

0 4

0 6

0 8

0 1

0 2

0 3

0 4

0 5

0 6

0 7

0 8

0 9

0 5

1 5

2 5

3 5

x 10

−3

analytic numer c dx=1 32 dy=1/32 dt=1 64 eta=0

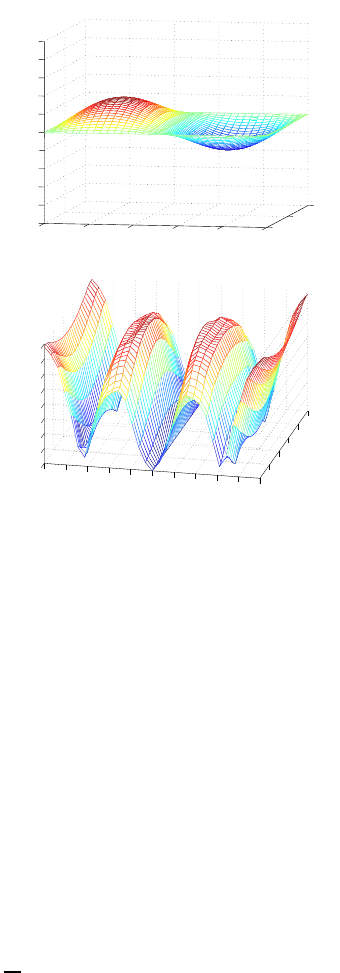
FIGURE 6.11: Numerical resolution of the wave equation: the numerical

approximation (left ﬁgure) and error functions (right ﬁgure) for the Neumann

boundary (right) (Δx =Δy =1/32, τ

=1/64, D

=1,D

=0.5, coupled

version).

The reference solution is obtained by executing the ﬁnite diﬀerences method

and setting Δx =1/256, Δy =1/256 and a time-step τ

=1/256 < 0.390625.

The model domain is given by a rectangle with Δx =1/16 and Δy =1/32.

The time-steps are given by τ

=1/16 and 0 ≤ η ≤ 0.5.

The numerical results for the Dirichlet boundary conditions are given in

Tables 6.26, 6.27, 6.28 and Figure 6.12.

The results show the second-order accuracy and the similar results of the

nonsplitting method (see Table 6.26) and classical splitting method (see Table

6.27). Therefore, the splitting method did not inﬂuence the numerical results,

as a preserving second-order method. The results can be improved by the LOD

method (see Table 6.28), while it reaches fourth-order accurate results with

the parameter η =

The numerical results for the Neumann boundary conditions are given in

Tables 6.29, 6.30 and Figure 6.13. We obtain the same results as shown in the

Dirichlet case. The second-order accuracy of the classical splitting method

(see Table 6.30) did not inﬂuence the second-order numerical results. The

Numerical Experiments 153

TABLE 6.26: Numerical

results for ﬁnite diﬀerences method

with spatial dependent parameters

and a Dirichlet boundary (error of

the reference solution).

η err

exact

num

0.0 0.0032 −0.7251 −0.7154

0.1 0.0034 −0.7251 −0.7149

0.3 0.0037 −0.7251 −0.7139

0.5 0.0040 −0.7251 −0.7129

TABLE 6.27: Numerical

results for classical

operator-splitting method with

spatial dependent parameters and a

Dirichlet boundary (error of the

reference solution).

η err

exact

num

0.0 0.0032 −0.7251 −0.7154

0.1 0.0034 −0.7251 −0.7149

0.3 0.0037 −0.7251 −0.7139

0.5 0.0040 −0.7251 −0.7129

TABLE 6.28: Numerical results for

LOD method with spatial dependent

parameters and a Dirichlet boundary (error

of the reference solution).

η err

exact

num

0.00 0.0032 −0.7251 −0.7154

0.1 0.7809e-003 −0.7251 −0.7226

0.122 0.6793e-003 −0.7251 −0.7242

0.3 0.0047 −0.7251 −0.7369

0.5 0.0100 −0.7251 −0.7512

same improvement for the Neumann case to reach higher order can be done

with the LOD method, see [104].

REMARK 6.11 In our experiments, we have analyzed both the clas-

sical operator splitting and the LOD method, and showed that the LOD

154Decomposition Methods for Diﬀerential Equations Theory and Applications

0.5

0.2

0.4

0.6

0.8

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

numeric solution dx=1/32 dy=1/32 dt=1/64 eta=1

0.2

0.4

0.6

0.8

0.5

−3

−2

−1

x 10

analytic − numeric (dx=1/32 dy=1/32 dt=1/64 eta=1)

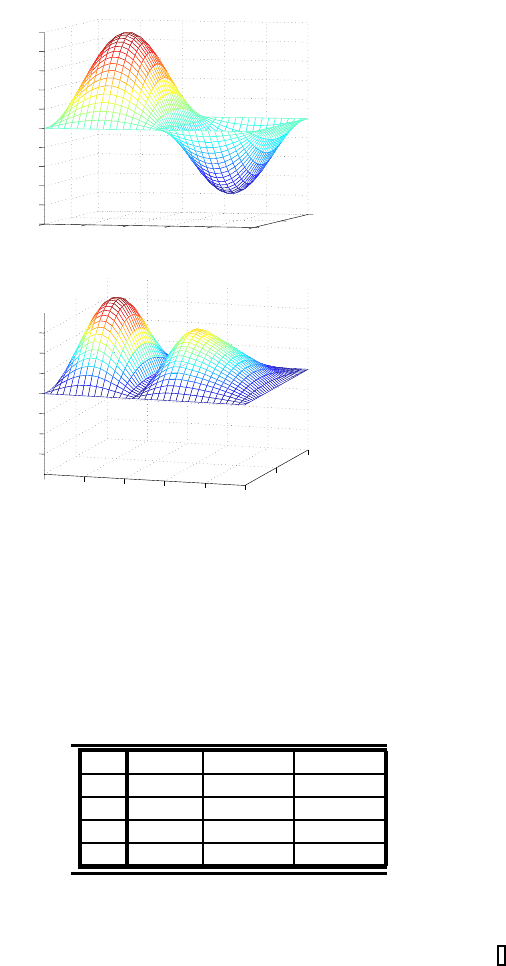
FIGURE 6.12: Dirichlet boundary condition: numerical solution (right

ﬁgure) and error function (left ﬁgure) for the spatial dependent test example.

TABLE 6.29: Numerical

results for ﬁnite diﬀerences method

with spatial dependent parameters

and Neumann boundary (error of

the reference solution).

η err

exact

num

0.0 0.0180 −0.7484 −0.7545

0.1 0.0182 −0.7484 −0.7532

0.3 0.0185 −0.7484 −0.7504

0.5 0.0190 −0.7484 −0.7477

method yields more accurate values.

REMARK 6.12 We have presented diﬀerent time splitting methods

for the spatial dependent case of the wave equation. The contributions of this

chapter concern the boundary splitting and the stiﬀ operator treatment. For

Numerical Experiments 155

TABLE 6.30: Numerical

results for classical

operator-splitting method with

spatial dependent parameters and

Neumann boundary (error of the

reference solution).

η err

exact

num

0.0 0.0180 −0.7484 −0.7545

0.1 0.0182 −0.7484 −0.7532

0.3 0.0185 −0.7484 −0.7504

0.5 0.0190 −0.7484 −0.7477

the boundary splitting method, we discussed the theoretical background, and

the experiments showed that the method is also stable for the stiﬀ case. We

presented stable results even for the spatial dependent wave equation. The

computational process beneﬁts from decoupling the stiﬀ and nonstiﬀ operators

into diﬀerent equations, due to the diﬀerent scales of the operators. The

LOD method as a fourth-order method has the advantage of higher accuracy

and can be used for such decoupling. In a future work, we will discuss the

algorithms based on the eigenmodes of the operators for more ﬂexibility in

decoupling problems.

6.4.2 Numerical Examples of the Elastic Wave Propagation

with Iterative Splitting Methods

We now apply the two- and three-dimensional iterative operator-splitting

methods to our wave equations. The time discretization is of second order,

and our splitting method is given for the two-dimensional equations as

n+1

) − 2u

+ u

n−1

= τ



∂

n+1

)

∂x

+(1− 2η)

∂

∂x

+ η

∂

n−1

∂x



(6.63)

+ τ



∂

i−1

n+1

)

∂y

+(1− 2η)

∂

∂y

+ η

∂

n−1

∂y



i+1

n+1

) − 2u

+ u

n−1

= τ



∂

n+1

)

∂x

+(1− 2η)

∂

∂x

+ η

∂

n−1

∂x



(6.64)

+ τ



∂

i+1

n+1

)

∂y

+(1− 2η)

∂

∂y

+ η

∂

n−1

∂y



156Decomposition Methods for Diﬀerential Equations Theory and Applications

0.2

0.4

0.6

0.8

0.5

−0.5

0.5

numeric solution (dx=1/32 dy=1/32 dt=1/32 eta=0.5)

0.2

0.4

0.6

0.8

0.5

−0.015

−0.01

−0.005

0.005

0.01

0.015

analytic − numeric (dx=1/32 dy=1/32 dt=1/32 eta=0.5)

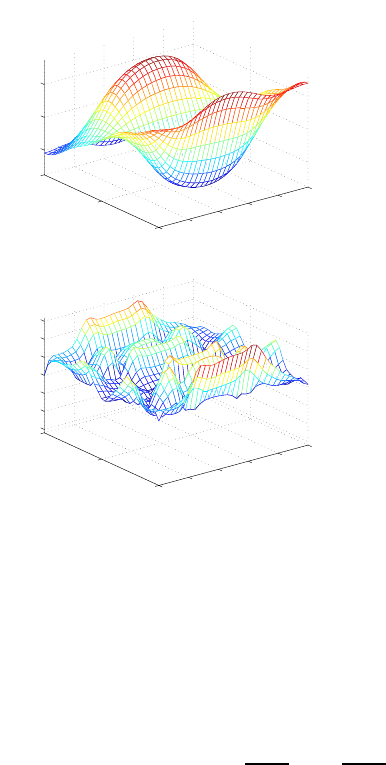
FIGURE 6.13: Neumann boundary condition: numerical solution (left ﬁg-

ure) and error function (right ﬁgure) for the spatial dependent test example.

where i =1, 3,...2m + 1, and the previous solutions are given as u

n−1

and

, the starting solution u

i−1

n+1

)isgivenas

i−1

n+1

) − 2u

+ u

n−1

= τ

∂

∂x

+ D

∂

∂y

The error is calculated by

err



i=1

Δx

· ...· Δx

|u(x

1,i

,...,x

d,i

) − u

exact

1,i

,...,x

d,i

) |,

(6.65)

where p is the number of grid points. u

exact

is the analytical solution, and

u is the numerical solution; Δx

,...,Δx

are the equidistant spatial steps of

each dimension.

In the following we present the simulations of test examples for the wave

equation with iterative splitting methods.