Geiser J. Decomposition Methods for Differential Equations: Theory and Applications
Подождите немного. Документ загружается.


Numerical Experiments 137
defined over Ω × [t
0
,T
f
]=Ω×[100, 10
5
], with an exact solution given as
u
exact
(x, t)=
u
0
2
√
Dπt
exp(−
(x − vt)
2
4Dt
)exp(−λt). (6.40)
The initial condition and the Dirichlet boundary condition are defined using
the exact solution (6.40) at the start time t
0
= 100 and with u
0
=1.0. The
reaction parameter is given as λ =10
−5
, where the convection parameter is
v =0.001 and the diffusion parameter is D =0.0001. The time interval is
given as [100, 10
5
]. The boundary condition is given by u(±∞,t)=0.
We considered the backward Euler discretization for both splitted opera-
tors (i.e., the convection and the diffusion reaction operator), to simulate the
solution over the time interval [100, 10
5
].
The model problem (6.38) is solved with both first-order operator-splitting
method (FOP) and first-order operator-splitting method with overlapping
Schwarz waveform-relaxation method (FOPSWR).
We compare the accuracy of the solution over the entire spatial domain
with different values for the spatial step Δx, and equidistant time-steps τ
using both the FOP method and the FOPSWR method over two subdomains
with different sizes of overlapping. The errors of the solution are given in Table
6.12 and Table 6.13, respectively. The FOPSWR method is considered over
two overlapping subdomains of different overlapping size L
2
−L
1
, to conclude
on the accuracy of the algorithm with the operator-splitting method. The
considered subdomains are Ω
1
=[0, 60] and Ω
2
=[30, 150], as well as Ω
1
=
[0, 100] and Ω
2
=[30, 150], see Figure 6.3. We apply the maximum norm,
L
∞
-norm, as an error norm for the error between the exact and numerical
solution.
Ω
21
Ω
22
Ω
11
Ω
12
Ω
Decomposed Domains
FIGURE 6.3: Overlapping situations for the numerical example.
The graphical output for the FOP method is presented in Figure 6.4. In
our numerical computations, we refined the time- and space-steps systemat-
ically in order to visualize the accuracy and error reduction throughout the
© 2009 by Taylor & Francis Group, LLC

138Decomposition Methods for Differential Equations Theory and Applications
TABLE 6.12: The L
∞
-error in time and space
for the convection-diffusion-reaction equation using
FOP method.
time-step err
u,L
∞
err
u,L
∞
err
u,L
∞
τ =5 0.001108 2.15813e-4 6.55262e-5
τ =10 0.00113 2.3942e-4 8.6641e-5
τ =20 0.001195 2.86514e-4 1.2868e-4
Spatial step Δx =1 Δx =0.5 Δx =0.25
FIGURE 6.4: The results for the FOP method plotted as solid line in
comparison with the exact solution plotted as dashed line, for Δx =1(left
figure) and Δx =0.5 (right figure).
simulation over the time interval for refined time- and space-steps. In Table
6.13 we observe that with the FOP method, the error reduced in first and
second order with respect to time and space.
For the solution with the FOPSWR method, using FOP method as basic
solver, the accuracy of the solution improved as the size of overlapping sub-
domains increased.
The results for the modified method are presented in Figure 6.5.
© 2009 by Taylor & Francis Group, LLC
Numerical Experiments 139
TABLE 6.13: The L
∞
-error in time and space for the scalar
convection-diffusion-reaction equation using FOPSWR method with two
different sizes of overlapping: 30 and 70.
Time-step err
u,L
∞
err
u,L
∞
err
u,L
∞
err
u,L
∞
err
u,L
∞
err
u,L
∞
τ =5 1.108e-3 1.08e-3 2.159e-4 2.158e-4 6.782e-5 6.552e-5
τ =10 1.138e-3 1.137e-3 2.397e-4 2.394e-4 8.681e-5 8.681e-5
τ =20 1.196e-3 1.195e-3 2.871e-4 2.865e-4 1.290e-4 1.286e-4
overlap. 30 70 30 70 30 70
Spatial step Δx =1 Δx =0.5 Δx =0.25
0 20 40 60 80 100 120
0
0 002
0 004
0 006
0 008
0 01
0 012
50 60 70 80 90 100 110 120 130 140 150
0
0 002
0 004
0 006
0 008
0 01
0 012
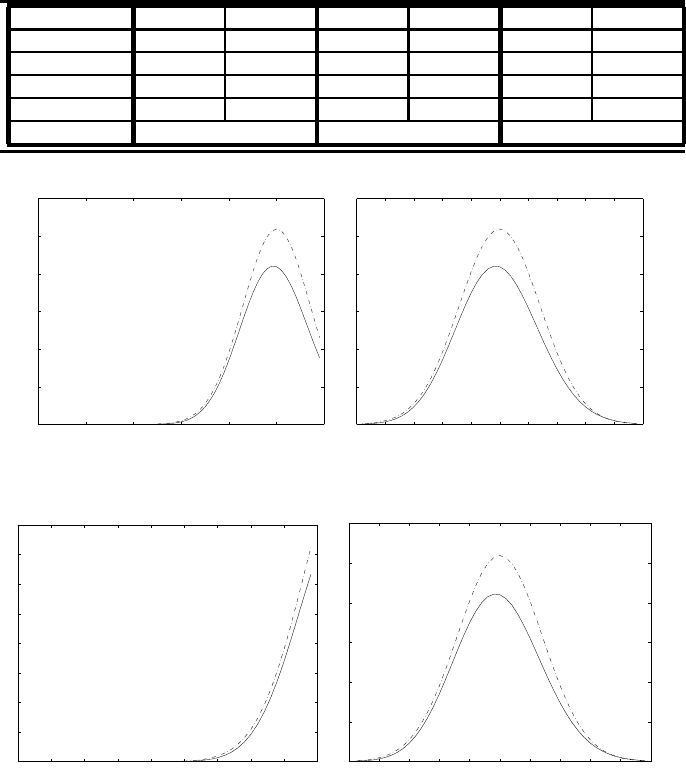
FIGURE 6.5: The results for FOPSWR method with overlapping size 30
plotted as solid line and the exact solution plotted as dashed line.
0 10 20 30 40 50 60 70 80 90
0
1
2
3
4
5
6
7
8
x 10
−3
50 60 70 80 90 100 110 120 130 140 150
0
0 002
0 004
0 006
0 008
0 01
0 012
FIGURE 6.6: The results for FOPSWR method with overlapping size 70
plotted as solid line and the exact solution plotted as dashed line.
6.3.2 Second Example: System of Convection-Diffusion-
Reaction Equations (Decoupled) Solved with
Operator-Splitting Methods
We consider a more complicated example of a one-dimensional convection-
diffusion-reaction equation:
R
i
∂
t
u
i
+ v∂
x
u
i
− ∂
x
D∂
x
u
i
= −R
i
λ
i
u
i
, (6.41)
u
i
(x, t
0
)=u
i
exact
(x, t
0
),u
i
(±∞,t)=0, (6.42)
© 2009 by Taylor & Francis Group, LLC
140Decomposition Methods for Differential Equations Theory and Applications
with the analytical solution given as (cf. [94])
u
i
exact
(x, t)=
u
i
in
2R
i
Dπt/R
i
exp(−
(x − vt/R
i
)
2
4 Dt/R
i
)exp((−λ
i
t)),(6.43)
for i =1andi =2.
For the initial conditions we have the parameters u
1
in
=1.0andu
2
in
=1.0
and the start time t
0
= 100. For boundary condition, we use the Dirichlet
boundary condition with 0.0. We have the equation parameters λ
1
=1.0·10
−5
,
λ
2
=4.0 · 10
−5
, v =0.001, D =0.0001, R
1
=2.0, and R
2
=1.0. The time
interval is defined with t ∈ [t
0
,t
end
]andt
end
=10
5
.
The results for the classical method (operator-splitting method) are given
in Table 6.14. In the next experiments, we consider the modified method.
TABLE 6.14: The L
∞
-error in time and space for the system of decoupled
convection-diffusion-reaction equations using FOP method.
Time-step err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
τ =5 4.461e-4 2.045e-4 3.466e-4 1.940e-4 9.110e-5 1.792e-4
τ =10 4.506e-4 2.055e-04 3.515e-4 1.948e-4 9.528e-5 1.794e-4
τ =20 4.594e-4 2.075e-4 3.611e-4 1.963e-4 1.036e-4 1.799e-4
Spatial step Δx =1 Δx =0.5 Δx =0.25
For the overlapping part, we obtain the overlap sizes of 30 and 70 that is,
Ω
1
= {0 <x<60} and Ω
2
= {30 <x<150}, while for the other case we
have Ω
1
= {0 <x<100} and Ω
2
= {30 <x<150}.
TheresultsaregiveninTable6.15.
TABLE 6.15: The L
∞
-error in time and space for the system of decoupled
convection-diffusion-reaction equations using FOPSWR method with the
overlapping size of 30.
Time-step err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
τ =5 4.461e-4 2.046e-4 3.466e-4 1.941e-4 9.110e-5 1.792e-4
τ =10 4.506e-4 2.056e-04 3.515e-4 1.948e-4 9.528e-5 1.795e-4
τ =20 4.594e-4 2.076e-4 3.611e-4 1.964e-4 1.036e-4 1.800e-4
Spatial step Δx =1 Δx =0.5 Δx =0.25
overlap. 30
The next result is given with the overlapping size of 70, see Table 6.16. By
comparing the results, we see that we can improve the computations with the
© 2009 by Taylor & Francis Group, LLC

Numerical Experiments 141
TABLE 6.16: The L
∞
-error in time and space for the system of decoupled
convection-diffusion-reaction equations using FOPSWR method with the
overlapping size of 70.
Time-step err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
err
u
2
τ =5 4.461e-4 2.046e-4 3.466e-4 1.941e-4 9.110e-5 1.792e-4
τ =10 4.506e-4 2.055e-04 3.515e-4 1.948e-4 9.528e-5 1.794e-4
τ =20 4.594e-4 2.075e-4 3.611e-4 1.963e-4 1.036e-4 1.800e-4
Spatial step Δx =1 Δx =0.5 Δx =0.25
overlap. 70
modified method and obtain higher-order results. Because of the decoupling,
each equation could be computed separately. For the first component, we
derive improved results because of the smaller reaction in the equation.
6.3.3 Third Example: System of Convection-Diffusion-
Reaction Equations (Coupled) Solved with Operator-
Splitting Methods
We deal with the more complicated example of a one-dimensional convection-
diffusion-reaction equation:
R
1
∂
t
u
1
+ v∂
x
u
1
− ∂
x
D∂
x
u
1
= −R
1
λ
1
u
1
, (6.44)
R
2
∂
t
u
2
+ v∂
x
u
2
− ∂
x
D∂
x
u
2
R
1
λ
1
u
1
− R
2
λ
2
u
2
, (6.45)
u
1
(x, t
0
)=u
1
exact
(x, t
0
) ,u
1
(±∞,t)=0,
u
2
(x, t
0
)=u
2
exact
(x, t
0
) ,u
2
(±∞,t)=0,
The analytical solution is given as (cf. [94])
u
1
exact
(x, t)=
u
1
in
2R
1
Dπt/R
1
exp(−
(x − vt/R
1
)
2
4 Dt/R
1
)exp((−λ
1
t)),
u
2
exact
(x, t)=
u
2
in
2 R
2
Dπt/R
2
exp(−
(x − vt/R
2
)
2
4 Dt/R
2
)exp((−λ
2
t))
+
R
1
λ
1
u
1
in
2
Dπ(R
1
− R
2
)
exp(
xv
2D
)exp(
−(R
1
λ
1
− R
2
λ
2
) t
(R
1
− R
2
)
)(W (v
2
) − W (v
1
)),
v
1
=
R
1
λ
1
−
(R
1
λ
1
−R
2
λ
2
)
R
1
−R
2
R
1
+ v
2
/(4D),
v
2
=
R
2
λ
2
−
(R
1
λ
1
−R
2
λ
2
)
R
1
−R
2
R
2
+ v
2
/(4D),
W (v)= 0.5(exp(−
xvv
2 D
)erfc(
x−v v t
√
4 Dt
)+exp(
xvv
2 D
)erfc(
x+v v t
√
4 Dt
)) ,
© 2009 by Taylor & Francis Group, LLC

142Decomposition Methods for Differential Equations Theory and Applications
where erfc(·) is the known error function, see [1], and we have the following
conditions: R
1
>R
2
and λ
2
>λ
1
.
For the initial conditions we have the parameters u
1
in
=1.0, u
2
in
=0.0, and
the start time t
0
= 100. For the boundary condition, we use the Dirichlet
boundary condition with the value 0.0. We have the equation parameters
λ
1
=1.0 · 10
−5
, λ
2
=4.0 · 10
−5
, v =0.001, D =0.0001, R
1
=2.0, and
R
2
=1.0. The initial conditions are given as u
10
=1.0andu
20
=0.0. The
time interval is defined by t ∈ [t
0
,t
end
]andt
end
=10
5
.
In the following tables, we compare the classical with the modified method,
and we test different reaction parameters and different splitting orders.
The results for the classical method (operator-splitting method) are given
in Table 6.17.
TABLE 6.17: The L
∞
-error in time and space for the system of
convection-diffusion-reaction equations using FOP method, with
λ
1
=2.0 · 10
−5
,λ
2
=4.0 · 10
−5
.
Time-step err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
L
∞
err
u
1
,L
∞
err
u
2
,L
∞
τ =5 4.461e-4 2.403e-3 3.466-4 2.452e-3 9.110e-5 2.702e-3
τ =10 4.506e-4 2.39e-3 3.515e-4 2.447e-3 9.528e-5 2.697e-3
τ =20 4.594e-4 2.8e-3 3.611e-4 2.438e-3 1.036e-4 2.689e-3
Spatial step Δx =1 Δx =0.5 Δx =0.25
The results for the modified method (operator-splitting method and domain
decomposition method) are given in Table 6.18.
TABLE 6.18: The L
∞
-error in time and space for the system of
convection-diffusion-reaction equations using FOPSWR method, with
λ
1
=2· 10
−5
,λ
2
=4· 10
−5
.
Time-step err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
τ =5 4.461e-4 2.403e-3 3.466e-4 2.452e-3 9.110e-5 2.702e-3
τ =10 4.506e-4 2.398e-3 3.515e-4 2.447e-3 9.528e-5 2.697e-3
τ =20 4.594e-4 2.388e-3 3.611e-4 2.438e-3 1.036e-4 2.689e-3
Spatial step Δx =1 Δx =0.5 Δx =0.25
overlap. 70
We can compare the results and improve the computations using modified
method to obtain higher-order results.
© 2009 by Taylor & Francis Group, LLC
Numerical Experiments 143
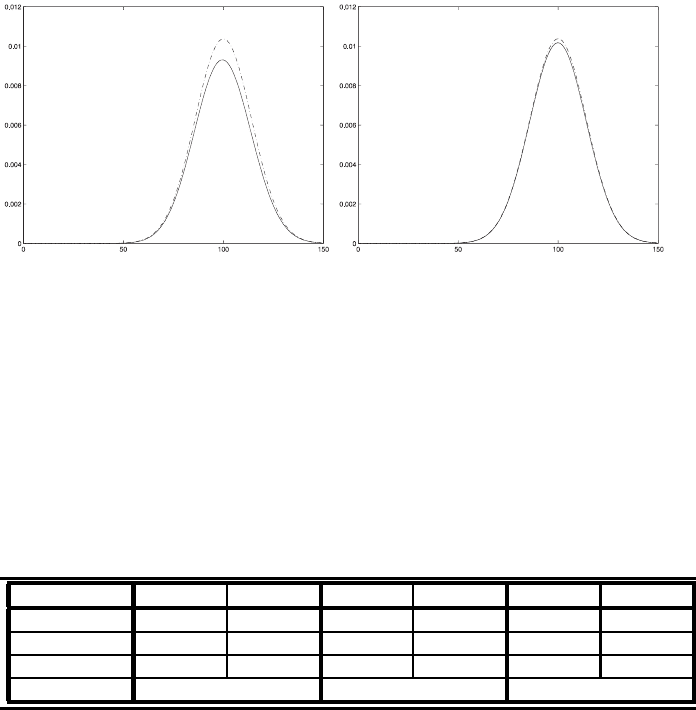
In Figure 6.7, the results for solutions with different time-steps are pre-
sented. We run a second experiment with modified reaction parameters to
FIGURE 6.7: The results for FOP method plotted as solid line for the
different steps Δx =1(leftfigure)andΔx =0.5 (right figure) and the exact
solution plotted as dashed line.
observe the influence of the first and the second components.
We use the classical second-order splitting method in the first computation;
the results are shown in Table 6.19. In the second computation, we use the
TABLE 6.19: The L
∞
-error in time and space for the system of
convection-diffusion-reaction equations using SOP method, with
λ
1
=1.0 · 10
−9
,λ
2
=4.0 · 10
−5
.
Time-step err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
τ =5 3.297e-3 6.058e-7 2.562e-3 6.192e-7 6.753e-4 6.820e-7
τ =10 3.30e-3 6.044e-7 2.599e-3 6.179e-7 7.083e-4 6.808e-7
τ =20 3.396e-3 6.018e-7 2.673e-3 6.152e-7 7.746e-4 6.784e-7
Spatial step Δx =2 Δx =1 Δx =0.5
modified method and obtain the results shown in Table 6.20. In the Tables
6.19 and 6.20 we see higher-order results in space for the first component.
The first component has an important influence on the second component,
and we find that decreasing the error of the second component decreases the
error of the first component. The results for the modified method are shown
in Figure 6.18. The very strong coupling of the equation causes the methods
to be of second order, because the error reduces and the computations are
more effective.
© 2009 by Taylor & Francis Group, LLC
144Decomposition Methods for Differential Equations Theory and Applications
TABLE 6.20: The L
∞
-error in time and space for the system of
convection-diffusion-reaction equations using SOPSWR method with
λ
1
=1.0 · 10
−9
,λ
2
=4·10
−5
.
Time-step err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
err
u
1
,L
∞
err
u
2
,L
∞
τ =5 3.297e-3 6.058e-7 2.545e-3 6.192e-7 6.753e-4 6.820e-7
τ =10 3.314e-3 6.044e-7 2.599e-3 6.179e-7 7.083e-4 6.808e-7
τ =20 3.380e-3 6.018e-7 2.673e-3 6.152e-7 7.746e-4 6.784e-7
Spatial step Δx =2 Δx =1 Δx =0.5
overlap. 70
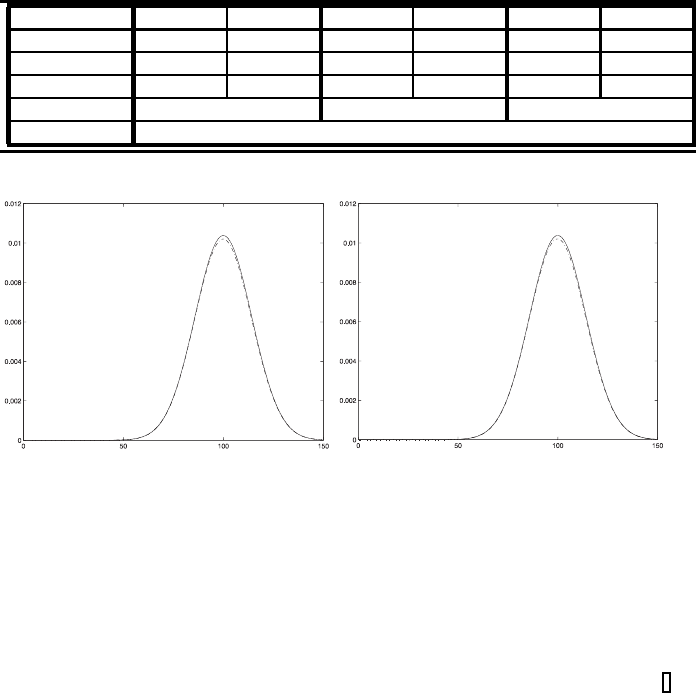
FIGURE 6.8: The results for SOP method plotted as the solid line for
different time-steps τ = 10 (left figure) as well as τ = 20 (right figure) and
the exact solution is plotted with the dashed line.
REMARK 6.7 The efficient results are taken with the spatial and
time decomposition methods. The first-order splitting methods in time are
sufficient to reach the efficient results because of the higher spatial error.
Second-order splitting in time and more waveform-relaxation steps in space
can obtain finer spatial discretization and reach higher-order results.
© 2009 by Taylor & Francis Group, LLC
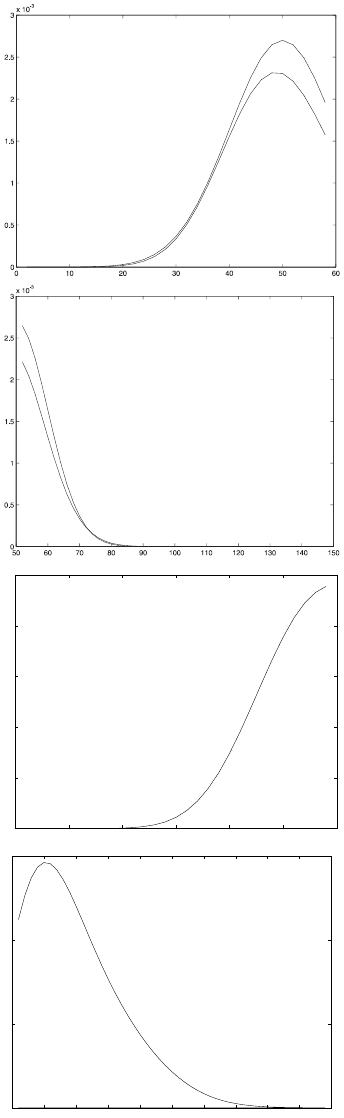
Numerical Experiments 145
0 10 20 30 40 50 60
0
0 5
1
1 5
2
2 5
x 10
3
50 60 70 80 90 100 110 120 130 140 150
0
0 5
1
1 5
x 10
3
FIGURE 6.9: In the upper figures the results of the first component
performed with SOPSWR method and plotted with the lower solid line and
the analytical solution plotted with the upper solid line are shown, where in
the lower figures we have the results of the second component performed
with SOPSWR method and plotted with the solid line.
© 2009 by Taylor & Francis Group, LLC
146Decomposition Methods for Differential Equations Theory and Applications
6.4 Benchmark Problems for the Temporal
Decomposition Methods for Hyperbolic
Equations
In this section, we will present the benchmark problems for the time de-
composition methods for hyperbolic equations.
We are interested in the spatial dependent wave equation:
∂
2
u
∂t
2
= D
1
(x)
∂
2
u
∂x
2
1
+ ...+ D
d
(x)
∂
2
u
∂x
2
d
,t∈ [0,T],x∈ Ω,
u(x, 0) = u
0
(x),x∈ Ω, (6.46)
∂
t
u(x, 0) = u
1
(x),x∈ Ω,
u(x, t)=u
2
(x, t),t∈ [0,T],x∈ ∂Ω
D
,
∂
n
u(x, t)=0,t∈ [0,T],x∈ ∂Ω
N
,
where x =(x
1
,...,x
d
)
T
∈ Ω, the initial functions are given as u
0
,u
1
:Ω→
R
+
, and the function for the Dirichlet boundary is u
2
:Ω×[0,T] → R
+
.The
domain Ω ⊂ R
d
is Lipschitz continuous and convex, and the time interval is
[0,T] ⊂ R
+
. The boundary is given as ∂Ω=∂Ω
D
∪ ∂Ω
N
.
For constant wave parameters (i.e., D
1
,...,D
d
∈ R
+
)wecanderivethe
analytical solution given as
u(x
1
,...,x
d
,t)=sin(
1
√
D
1
πx
1
) · ...· sin(
1
√
D
d
πx
d
) · cos(
√
dπt). (6.47)
We compute a reference solution for the nonconstant wave parameters with
sufficiently fine grids and small time-steps, see [178].
We now discuss the noniterative and iterative splitting methods for two-
dimensional and three-dimensional wave equations.
6.4.1 Numerical Examples of the Elastic Wave Propagation
with Noniterative Splitting Methods
In the following we present the simulations of test examples for the wave
equation with noniterative splitting methods.
© 2009 by Taylor & Francis Group, LLC
