Гашков С.Б. Современная элементарная алгебра в задачах и решениях

Подождите немного. Документ загружается.

§ 1.8. Сочетания и разбиения 51

26**. (Чебышёв.) Докажите, что сумма по всем простым p, не пре

восходящим n, слагаемых lg p

p больше, чем C lg n, где C

––

некоторая

константа.

У к а з а н и е.

√

n! > n

27**. (Чебышёв.) Докажите, что сумма по всем простым p, не пре

восходящим n, слагаемых 1

p больше, чем C lg lg n, где C

––

некоторая

константа.

У к а з а н и е. Если P

––

множество всех простых чисел, S

––

множе

ство всех квадратов, F

––

множество всех чисел, не делящихся на квад

раты, то

k=1

k∈S

k=1

k∈F

k=1

;

exp

k=1

k∈P

k=1

k∈P

exp

k=1

k∈P



1 +



k=1

k∈F

§ 1.8. Сочетания и разбиения

Обозначим через P

(A) множество {M: M ⊂A, |M|= k} всех подмно

жеств множества A, имеющих мощность k, другими словами, k

подмно

жеств.

Определение 26. Элементы множества P

(A) называются сочета-

ниями элементов из A по k.

Теорема 18 (о числе k

подмножеств). Справедливо равенство

(A)|= C

|A|

Д о к а з а т е л ь с т в о. Пусть A = {a

, . . ., a

|A|

}. Сопоставим каждо

му сочетанию M из P

(A) слово α

... α

|A|

∈{0, 1}

|A|

такое, что α

= 1

тогда и только тогда, когда элемент a

принадлежит M. Таким образом,

построено взаимно однозначное отображение из множества P

(A) в мно

жество S(k, |A|−k). В силу теоремы 14 имеем |P

(A)|= C

|A|

Теорема 19 (об упорядоченных разбиениях). Число решений

уравнения x

+ ... + x

= k в натуральных числах равно C

n−1

k−1

Д о к а з а т е л ь с т в о. Сопоставим каждому набору (x

, ..., x

)

слово

0 ... 0

{z }

−1

1 0 ... 0

{z }

−1

1 ... 1 0 ... 0

{z }

−1

∈{0, 1}

k−1

52 Глава I. Числа и комбинаторика

Таким образом построено взаимно однозначное отображение из мно

жества всех решений уравнения в множество S(n −1, k −n). Остается

применить теорему 14.

Теорема 20 (о разбиениях на неотрицательные слагаемые). Чис-

ло решений уравнения x

+ ... + x

= k в целых неотрицательных

числах равно C

n−1

n+k−1

Д о к а з а т е л ь с т в о. Сопоставим каждому набору (x

, .. ., x

) це

лых неотрицательных чисел набор (y

, ..., y

) натуральных чисел, где

= x

+ 1, i = 1, ..., k. Тем самым установлено взаимно однозначное со

ответствие множества всех целых неотрицательных решений уравнения

+ ... + x

= n и множества всех решений уравнения y

+ .. . + y

= n + k

в натуральных числах. Остается применить теорему 19.

Следствие из теоремы 20. Число слагаемых в полиномиальной

формуле равно C

k−1

n+k−1

Пример. Сочетания с повторениями появляются при решении сле

дующей задачи имеется kn шаров n различных цветов, по k штук каж

дого цвета. Сколькими различными способами из них можно выбрать k

шаров?

Р е ш е н и е. Каждой выборке сопоставим упорядоченный набор

, ... , x

), такой, что x

+ ... + x

= k, где x

––

число шаров в выбор

ке, имеющих i

й цвет. Тем самым установлено взаимно однозначное

соответствие между числом выборок и числом решений уравнения

+ ... + x

= k в неотрицательных целых числах. Значит, число вы

борок, согласно теореме 20, равно C

n−1

n+k−1

= C

n+k−1

Определение 27. Это число называется числом сочетаний с по-

вторениями из n по k.

Упражнение 19. Проверьте тождество C

n+k−1

= [n]

k!.

Задачи и упражнения к § 1.8

1. Числовую последовательность назовем монотонной, если каждое

следующее число не меньше предыдущего. Докажите, что число моно

тонных последовательностей длины k, не содержащих чисел отличных

от 1, ..., n, равно C

n+k−1

= [n]

k!.

2. Сколькими способами можно разместить n одинаковых шаров

по m разным урнам?

3. Вычислите

⌊n

2⌋

k=0

⌊(n−1)

2⌋

k=0

2k+1

§ 1.8. Сочетания и разбиения 53

4. Используя теорему 18, докажите тождество Паскаля

= C

n−1

+ C

k−1

n−1

и тождество Вандермонда *

k=0

n−k

m−l

5. Вычислите коэффициент при x

в многочлене (1 + x + x

)

6. Решите задачу 4, используя биномиальную теорему и тождество

(1 + x)

= (1 + x)

· (1 + x)

m−l

7. Найдите сумму квадратов чисел n

й строки треугольника Паскаля.

8. Докажите тождество для n

го континуанта

[x, ..., x

{z }

] =

⌊n

2⌋

k=0

n−k

n−2k

У к а з а н и е. Можно применить задачу 4 из § 1.4.

9. В треугольнике Паскаля найдите числа Фибоначчи, правда, не в

явном виде, а виде суммы чисел по диагоналям.

1 1

1 2 1

1 3 3

1 4 6 4 1

5 10 10 5 1

6 15 20 15 6 1

Рис. 6. Диагональ

в треугольнике Паскаля

Докажите, что

k=0

n−k

= F

n+1

У к а з а н и е. Можно применить предыду

щую задачу.

10. Используя тождество Паскаля, до

кажите, что

= C

n−1

+ C

k−1

n−2

+ ... + C

n−k

+ 1.

Проверьте, что это равенство верно при n = k, если положить C

= 0 при

k > m.

11. Докажите, что многочлен ((x + y)

+ 3x + y)

2 осуществляет вза

имно однозначное отображение (биекцию) множества N

= N ×N всех

упорядоченных пар натуральных чисел на множество N = {0, 1, 2, . ..}.

12**. Используя задачу 10, докажите, что многочлен

p(x

, ..., x

) = C

+. . .+x

+k−1

+ C

k−1

+. . .+x

k−1

+k−2

+ ... + C

+ C

* А. Вандермонд (Alexandre Théophile Vandermonde, 1735

–

1796)

––

французский мате

матик, член Парижской академии наук.

54 Глава I. Числа и комбинаторика

осуществляет биекцию множества N

= N ×... ×N всех наборов нату

ральных чисел длины k на множество N = {0, 1, 2, ...}. Докажите, что

многочлен меньшей степени не может осуществлять такой биекции.

13*. Установите взаимно однозначное соответствие между множе

ством рациональных чисел и множеством натуральных чисел.

14*. Назовем цепью любую строго расширяющуюся последова

тельность множеств, начинающуюся с A

= ∅ и заканчивающуюся

= {1, ..., n}. Докажите, что

а) число всех таких цепей n!;

б) число цепей, в которые входит заданное k

элементное множество,

равно k!(n −k)!;

в) число k

элементных подмножеств в {1, ..., n} равно C

(вывести

из б)).

15*. (Шпернер *.) Докажите, что если есть семейство попарно не со

держащих друг друга подмножеств в {1, . .., n}, то их число не превосхо

дит C

⌊n

2⌋

У к а з а н и е. Пусть U

––

шпернерово семейство и для любого мно

жества A из семейства U множество Ц(A) состоит из цепей, проходящих

через A, тогда для любых множеств A, B из семейства U

Ц(A) ∩Ц(B) = ∅

и можно применить задачу 14.

16. В классе все учатся на 4 и 5 и никто не учится лучше другого.

Какое наибольшее число учеников может быть в классе, если изучаются n

предметов?

17*. Индукцией по n докажите формулу включения

исключения **



[

i=1



|−

i< j

∩A

i< j<k

∩A

|−... + (−1)

n−1

∩... ∩ A

Сколько слагаемых в m

й по счету сумме?

18. (Эйлер.) Используя задачу 17, докажите, что число правильных

несократимых дробей со знаменателем n равно ϕ(n) = n(1 −1

) ·. ..

... · (1 −1

), где p

, ... p

––

все различные простые делители n.

* Немецкий математик Э. Шпернер доказал эту теорему в 20

е годы XX в.

** Эту формулу первым получил французский математик А. де Муавр (Abraham

de Moivre, 1667

–

1754), проживший почти всю жизнь в Англии.

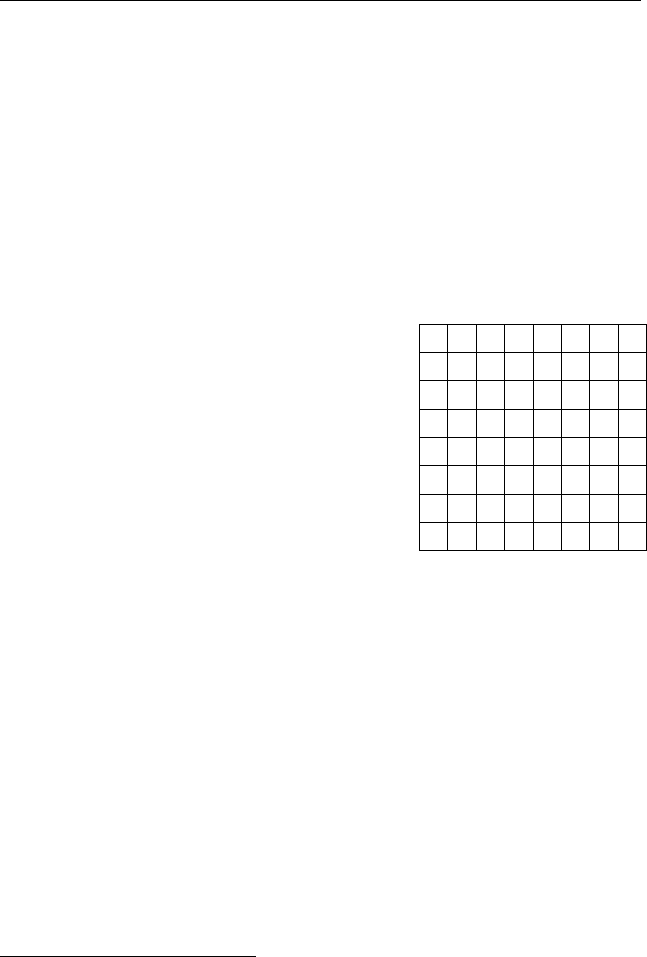
§ 1.8. Сочетания и разбиения 55

19. Обозначим N(n, k) число всех отображений из {1, .. ., n} в {1, ...

... , k}, являющихся наложениями. Докажите, что

а) N(n, n) = n!; б) N(n, n −1) = C

(n −1)!;

в) N(n, k) = k



N(n −1, k −1) + N(n − 1, k)



;

г) N(n, k) =

j=0

(−1)

(k − j)

У к а з а н и е. Применить задачу 17.

20. План города имеет вид прямоугольника, разбитого улицами на nm

одинаковых кварталов. Сколькими способами можно проехать из одного

угла города в противоположный угол, преодолев кратчайшее расстояние

(см. рис. 7)?

- -

- - - -

Рис. 7. Один из маршрутов

21. Используя задачу 17, решите зада

чу 4.

22. В каждую клетку шахматной дос

ки размера n ×n запишем число различ

ных кратчайших маршрутов движения ладьи

из левого верхнего угла доски до этой клетки.

Докажите, что половина доски, лежащая над

побочной диагональю, будет заполнена в точ

ности как треугольник Паскаля. Вся же доска

целиком будет изображать таблицу, называе

мую прямоугольником Тартальи * (см. рис. 8).

1 1 1 1 1 1

1 2 3 4 5 6

1 3 6 10 15 21

1 4 10 20 35 56

1 5 15 35 70 126

1 6 21 56 126 252

1 7 28 84 210 462

1 8 36 120 330 792

Рис. 8. Прямоугольник

Тартальи

23. Сколькими способами может попасть

на восьмую горизонталь шахматной доски

шашка, начинающая движение:

а) из угловой клетки первой горизонтали;

б) из средней клетки первой горизонтали;

в) из средней клетки диагонали доски.

Решите задачу для доски n ×n.

24. Введем обозначение a

n|h

= a(a −h) . . .

... (a − (n −1)h). Докажите факториальную

биномиальную теорему

(a + b)

n|h

k=0

k|h

(n−k)|h

25. Сколько разных бус можно составить из n различных бусинок?

* Н. Тарталья (Niccolo Tartaglia, ок. 1499

–

1557)

––

знаменитый итальянский математик,

его имя еще встретится нам в главе IV.

56 Глава I. Числа и комбинаторика

Дополнительные задачи по комбинаторике

1. Сколькими способами можно раскрасить в n цветов вершины

куба?

∗

. (Эйлер.) Сколькими способами можно разбить выпуклый

(n+2)

угольник на треугольники непересекающимися диагоналями?

∗

. (Каталан

∗

.) Сколькими способами можно расставить скобки

в произведении (n + 1) сомножителей?

∗

. (Кэли.) Дерево называется бинарным, если из одной его вершины

выходит 2 ребра, а из всех невисячих вершин

––

по 3 ребра. Найдите число

различных бинарных деревьев с n + 1 занумерованной висячей вершиной.

∗

. Сколькими способами можно провести шашку из одного угла дос

ки размера (2n + 1) × (2n + 1) в соседний угол?

У к а з а н и е. Обозначим координаты углов (0, 0) и (2n, 0) и дополним

доску клетками с отрицательными абсциссами, тогда число всех путей

из (0, 0) в (2n, 0) равно C

, а число путей, выходящих за край реаль

ной доски, равно числу всех путей из (0, −2) в (2n, 0), т. е. C

n−1

, так

как симметрия относительно прямой x = −1 переводит начальный отрезок

выходящего за край доски пути от (0, 0) до первой клетки с абсциссой −1

в начальный отрезок пути из (0, −2) в (2n, 0).

∗

. Докажите, что задачи 2

–

5 имеют одинаковый ответ: число Ката

лана

−C

n−1

n + 1

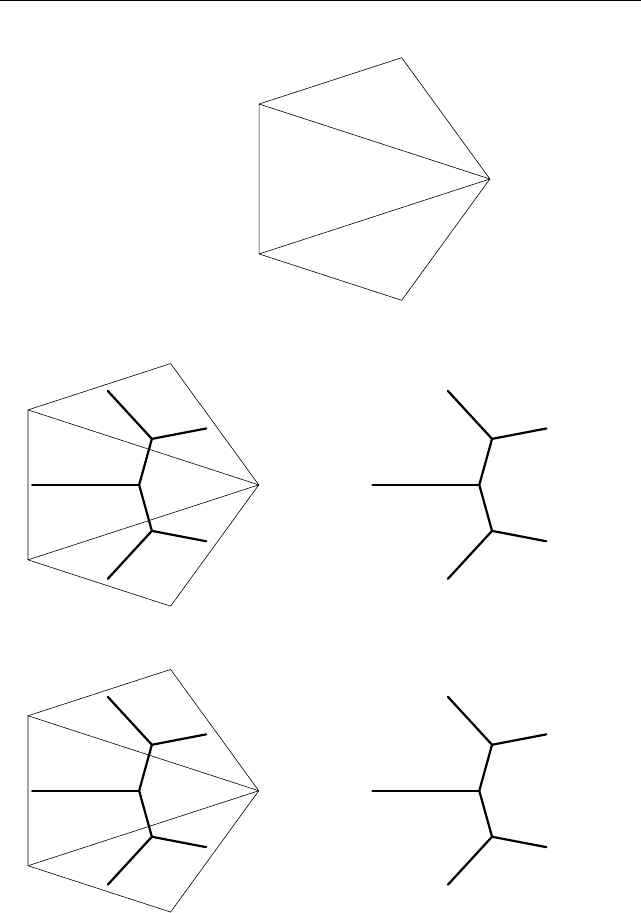
У к а з а н и е. Установите взаимно однозначное соответствие между

множествами из задач 2

–

5 с помощью рис. 9

–

11.

На рис. 11 левой скобке соответствует единица, правой

––

нуль, еди

нице соответствует движение шашки вправо, а нулю

––

влево.

Положим µ

(

)

= 0, если n делится на квадрат простого, µ

(

)

(

−1

)

если n

––

произведение k различных простых чисел, и µ

(

)

= 1 (это так

называемая функция Мёбиуса **).

7. Докажите, что сумма µ(d) по всем натуральным d, делящим n,

равна 0 при n > 1 и равна 1 при n = 1.

∗

. (Формула Мёбиуса

––

Чебышёва

––

Дедекинда

∗∗∗

.) Если при любом

x > 1 имеем g(x) =

[x]

n=1

f(x

n), то f(x) =

[x]

n=1

µ(n) g(x

n).

* Э. Ш. Каталан (Eugène Charles Catalan, 1814

–

1894)

––

бельгийский математик.

** А. Ф. Мёбиус (Augustus Ferdinand Möbius, 1790

–

1868)

––

немецкий математик

и астроном, изобретатель ленты Мёбиуса.

*** Эта формула была в явном виде опубликована Р. Дедекиндом, а еще раньше

––

П. Л. Чебышёвым.

§ 1.8. Сочетания и разбиения 57

a(b(cd)) ⇔

(cd)

b(cd)

a(b(cd))

Рис. 9. Триангуляция

a(b(cd))

Рис. 10. Триангуляция и дерево

a(b(cd))

Рис. 11. Дерево, формула, путь шашки и двоичная последовательность

58 Глава I. Числа и комбинаторика

∗

. (Другой вариант этой формулы.) Если при любом n

g(n) =

d|n

f(d),

то

f(n) =

d|n

µ(n) g(n

d).

∗

. (Макмагон

∗

.) Сколько разных бус (замкнутых ожерелий) можно

составить из n бусинок двух разных цветов:

а) при простом n; в) при n = pq, где p, q

––

простые;

б) при n = p

, где p

––

простое; г) в общем случае?

∗

. (Куммер

∗∗

.) Докажите, что

а) ord

= (ν

(n −k) + ν

(k) −ν

(n))

(p − 1), где ord

––

наи

больший показатель степени простого числа p, делящей a, а ν

(n)

––

сумма цифр p

ичной позиционной записи числа n;

б) число (ν

(n −k) + ν

(k) − ν

(n))

(p − 1) равно количеству перено

сов в следующий разряд при сложении чисел k и n −k в p

ичной системе

счисления, причем и при составном p.

12. Докажите, что биномиальный коэффициент C

нечетен тогда

и только тогда, когда в двоичной записи числа k единицы не стоят в тех

разрядах, где в числе n стоят нули.

13. Докажите, что биномиальный коэффициент C

не кратен просто

му числу p тогда и только тогда, когда в p

ичной записи числа k все

разряды не превосходят соответствующих разрядов числа n.

14. Докажите, что в ряду биномиальных коэффициентов

, ..., C

все числа нечетны тогда и только тогда, когда n = 2

−1.

15. Докажите, что в ряду биномиальных коэффициентов

, ..., C

все числа не кратны заданному простому p тогда и только тогда, когда n

равно mp

−1, где натуральное m < p.

16. Докажите, что в ряду биномиальных коэффициентов

, ..., C

* Майор П. А. Макмагон

––

известный английский специалист по комбинаторике. Пре

подавал в военной академии.

** Э. Куммер (Ernst Eduard Kummer, 1810

–

1893)

––

выдающийся немецкий математик.

Чл.

корр. Петербургской академии наук. Создал теорию алгебраических чисел и с помощью

ее доказал теорему Ферма для всех показателей вплоть до 100.

§ 1.9. Перестановки и подстановки 59

все числа, кроме первого и последнего, кратны заданному простому p

тогда и только тогда, когда n = p

17. Докажите, что в ряду биномиальных коэффициентов

, ..., C

количество нечетных чисел равно степени двойки.

18. Докажите, что в ряду биномиальных коэффициентов

, ..., C

количество не кратных p чисел равно (a

+ 1) .. . (a

+ 1), где числа

, ..., a

––

разряды p

ичной записи числа n, а число m =

= ⌈log

n⌉.

19. Докажите, что в первых p

−1 строках треугольника Паскаля

(т. е. среди биномиальных коэффициентов C

, k 6 m 6 p −1) количество

не кратных p чисел равно (p(p + 1)

20. (Люка.) Пусть p

––

простое, k 6 n

––

натуральные. Докажите, что

а)

∗

ord

= ord

и C

−C

кратно p;

б)

∗

−⌊n

p⌋ кратно p. Более того, если ⌊n

p⌋ кратно p

, то и C

тоже;

в)

∗∗

kp+s

np+m

−C

кратно p при неотрицательных n, m, k, s и при m

и s меньших p (биномиальный коэффициент равен нулю, если нижний

индекс меньше верхнего, а коэффициент C

по определению равен 1);

г)

∗∗

−C

... C

кратно p при

n = n

+ ... + n

p + n

, k = k

+ ... + k

p + k

0 6 n

, k

< p, 0 6 i 6 m;

д)

∗∗

−1

− (−1)

(k)

кратно p;

е)

∗∗∗

−C

кратно p

, а при p > 5

––

кратно и p

§ 1.9. Перестановки и подстановки

Множество всех перестановок множества E

= {1, 2, ..., n} обозначим

далее S

Произвольную перестановку π ∈S

можно представить в виде под

становки



1 2 ... n

π(1) π(2) ... π (n)



60 Глава I. Числа и комбинаторика

и изобразить с помощью двудольного графа, например, подстановку

„

123

231

можно изобразить как на рис. 12.









Рис. 12. Граф подстановки













Рис. 13. Умножение подстановок

Слова

перестановка

подстановка

для нас по существу будут

синонимами.

Определение 28. Если π

, π

∈S

––

произвольные перестановки,

то назовем их произведением и обозначим π

◦π

такую перестановку

π ∈S

, что для любого i из E

π(i) = π

(π

(i)).

Пример. Произведением подстановок

„

123

231

„

123

321

является под

становка

„

123

132

. В общем случае для умножения подстановки



1 2 ... n

(1) π

(2) ... π

(n)



на подстановку



1 2 ... n

(1) π

(2) ... π

(n)



нужно для каждого i = 1, ... , n выбрать из массива {π

(1), π

(2), ..., π

(n)}

(начинаем со второй подстановки!) i

й элемент π

[i], равный, напри

мер, j, а потом выбрать из массива {π

(1), π

(2), ..., π

(n)} j

й элемент

[j] = π

[π

[i]] и поместить его на i

е место в массив {π (1), π(2), . ..

..., π (n)}. Всего понадобилось 2n операций выборки элемента из массива

и n операций записи элемента в массив.

При устных вычислениях достаточно все это проделать при i = 1, ...

..., n −1, так как последний элемент результата определяется автомати

чески.

На рис. 13 изображено умножение подстановок

„

123

321

„

123

231



Порядок, в котором перемножаются перестановки, важен: произ

ведение π

◦π

может не совпадать с произведением π

◦π