Гашков С.Б. Современная элементарная алгебра в задачах и решениях

Подождите немного. Документ загружается.

§ 1.6. Комбинаторика отображений 41

a b c d e f g h

Рис. 2.

a b c d e f g h

Рис. 3.

a b c d e f g h

Рис. 4.

Произвольная последовательность обозначается обычно как {a

где a

называется ее n

м членом.

Примером последовательности является последовательность Фибо

наччи.

Определение 14. Для любого множества M, содержащегося в A,

множество {f(a): a ∈M} образов всех элементов M обозначим f(M) и на

зовем образом множества M.

Для первого отображения предыдущего примера f(A) ={a, b, c, . .., h},

а для второго f(A) = {a, c, e, g}.

Определение 15. Отображение f : A →B назовем наложением, ес

ли f(A) = B.

Первое отображение предыдущего примера является наложением,

а второе

––

не является.

Определение 16. Отображение f : A →B назовем вложением, если

разные элементы всегда имеют разные образы.

Первое отображение предыдущего примера является вложением,

а второе

––

нет.

Определение 17. Назовем отображение f : A →B взаимно одно-

значным отображением, если отображение f одновременно является

и вложением, и наложением.

Первое отображение предыдущего примера взаимно однозначно,

а второе

––

нет.

0 1 2

Рис. 5

П р и м е р ы. 1. График Γ

можно изобразить

в виде схемы, называемой двудольным графом,

например, если A = {0, 1, 2, 3}, B = {0, 1, 2}, Γ

= {(0, 0), (1, 0), (2, 1), (3, 2)}, то Γ

изображается

графом с четырьмя вершинами в одной доле и тре

мя

––

в другой (рис. 5).

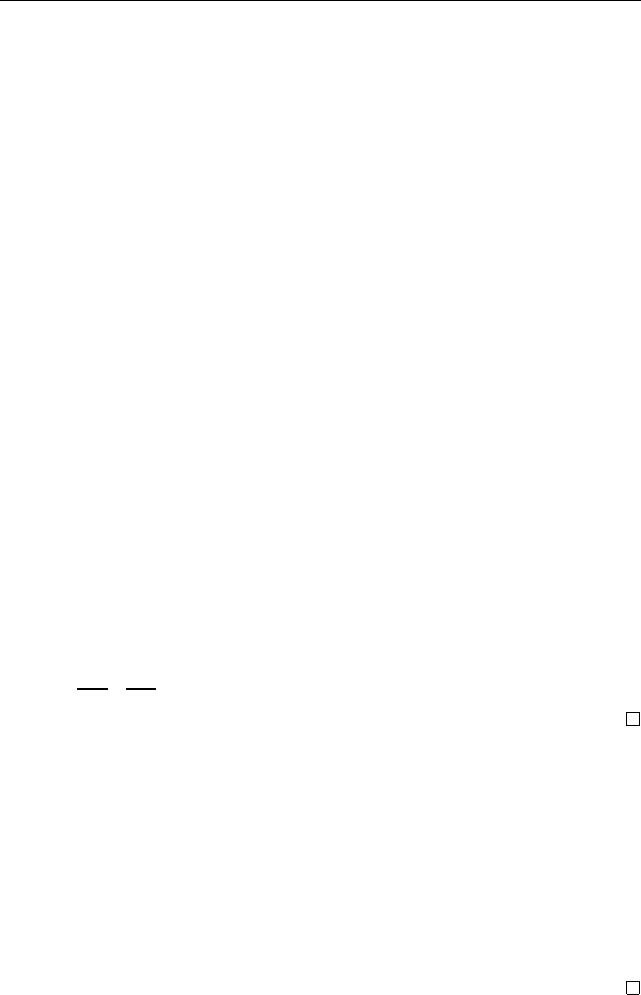
42 Глава I. Числа и комбинаторика

Отображение f является наложением, но не является вложением.

Образом множества {0, 1, 2} является множество {0, 1}.

2. Пример взаимно однозначного отображения

A = {1, 2, 3, 4, 5, 6, 7, 8} →B = {a, b, c, d, e, f, g, h}

представляет любая расстановка 8 ладей, не угрожающих друг другу.

Следующее определение применимо и к бесконечным множествам.

Определение 18. Если для множеств A и B существует взаимно

однозначное отображение f : A →B, то будем говорить, что A и B имеют

одинаковую мощность, и записывать это в виде |A|= |B|.

Большинство задач перечислительной комбинаторики могут быть

сформулированы как задачи о вычислении мощности данного конечного

множества.

На использовании понятия равномощности основан следующий прием

решения таких задач: если непосредственно мощность множества вычис

лить не удается, то пытаются установить взаимно однозначное отобра

жение этого множества с другим множеством, мощность которого уже

известна или может быть непосредственно вычислена. Далее мы будем

неоднократно пользоваться этим приемом.

Обозначим через F(A, B) множество всех отображений из A в B.

Имеет место следующая теорема.

Теорема 10. Для любых конечных множеств A и B справедливо

равенство |F(A, B)|= |B|

|A|

Д о к а з а т е л ь с т в о. Пусть A = {a

, ..., a

|A|

}, B = {b

, .. ., b

|B|

}. Су

ществует взаимно однозначное отображение множества F(A, B) на мно

жество B ×.. . × B

{z }

|A|

= B

|A|

. Из теоремы 8 следует, что

|F(A, B)|= |B

|A|

|= |B|

|A|

Обозначим через P(A) множество всех подмножеств множе-

ства A (включая само множество A и ∅

––

пустое подмножество). Имеет

место следующая

Теорема 11. Для конечного множества A справедливо равенство

|P(A)| = 2

|A|

Д о к а з а т е л ь с т в о. Сопоставим каждому подмножеству M мно

жества A его индикатор I

, т. е. такое отображение I

: A →{0, 1}, что

(a) = 1 тогда и только тогда, когда a принадлежит множеству M. По

лучаем взаимно однозначное отображение I : P(A) →F(A, {0, 1}). Из те

оремы 10 следует, что |P(A)| = 2

|A|

§ 1.6. Комбинаторика отображений 43

Кроме функций одной переменной, часто рассматриваются также

функции нескольких (иногда говорят

––

многих) переменных. Напри

мер, отображение f : A

→B можно рассматривать как функцию

f(x

, ..., x

) от n переменных x

∈A, 1 6 i 6 n. В частности, если

A = B = R, то такую функцию называют функцией n действительных

переменных.

П р и м е р ы. 1. В случае n = 1 график такой функции лежит в множе

стве R ×R = R

––

двумерном арифметическом пространстве (плоскости).

2. В случае n = 2 график такой функции лежит в множестве R

×R =

= R

––

трехмерном арифметическом пространстве (т. е. является поверх

ностью).

Для комбинаторики представляют интерес другие классы функций

многих переменных.

Определение 19. В случае A = B = E

= {0, 1} функция f(x

, ..., x

)

от n переменных, x

∈A, 1 6 i 6 n, называется функцией двузначной

логики, или функцией алгебры логики, а также еще булевой функ-

цией *.

В случае A = B = E

= {0, 1, ..., k −1} функция f(x

, ..., x

) n пере

менных, x

∈A, 1 6 i 6 n, называется функцией k-значной логики.

Задачи и упражнения к § 1.6

1. Сколько элементов (вершин) в n

мерном двоичном кубе?

2. Сколько элементов (вершин) в n

мерном k

ичном кубе?

3. Напишите таблицы всех булевых функций от двух переменных.

4. Сколько существует булевых функций от n переменных?

5. Сколько существует функций k

значной логики от n переменных?

6. Сколько различных n

значных чисел можно записать в десятичной

системе счисления (первая цифра отлична от 0)?

7. Пусть n = p

... p

. Найдите τ (n)

––

число всех натуральных де

лителей n и σ (n)

––

сумму этих делителей. Докажите, что если (m, n) = 1,

то τ (nm) = τ (n) ·τ (m) и σ (nm) = σ (n) ·σ (m).

8. Если p и 2

−1

––

простые, то n = 2

p−1

−1)

––

совершенное

число, т. е. такое, что σ(n) = 2n.

* Дж. Буль (George Boole, 1815

–

1864)

––

английский математик и логик, преподавал

в Ирландии. Отец писательницы Э. Л. Войнич.

44 Глава I. Числа и комбинаторика

Неизвестно, конечно или бесконечно множество четных совершенных

чисел. Самое большое из известных совершенных чисел (и соответствен

но самое большое из простых чисел Мерсенна *), найденное в 2001 г.,

получается при n = 13466917.

Нечетные совершенные числа до сих пор не найдены.

9. Докажите, что число всех пар подмножеств множества {1, 2, . . ., n}

таких, что первое из этих подмножеств содержится во втором, равно 3

10. Пусть p

––

простое число. Сколькими способами можно раскра

сить вершины правильного p

угольника, если разрешается использовать

заданные k цветов (не обязательно все) и две раскраски, переходящие

друг в друга при повороте p

угольника, считаются одинаковыми?

11. Выведите из предыдущей задачи, что p делит k

−k.

12. Произведение 1986 натуральных чисел имеет 1985 различных

простых делителей. Докажите, что произведение нескольких из этих

чисел либо одно из них являются квадратами натурального числа.

13*. Произведение 48 натуральных чисел имеет 10 различных про

стых делителей. Докажите, что произведение четырех из этих чисел яв

ляется квадратом натурального числа.

14*. Произведение 1985 натуральных чисел имеет 9 различных про

стых делителей.

а) Докажите, что можно выбрать 737 непересекающихся пар чисел,

произведения каждых из которых являются квадратами натуральных

чисел.

б) Докажите, что можно выбрать 113 непересекающихся четверок чи

сел так, что произведение каждой четверки будет четвертой степенью

натурального числа.

15*. На плоскости нарисованы n точек, занумерованных от 1 до n,

и некоторые из них соединены отрезками (ребрами) так, что ребра не пе

ресекаются (по внутренним точкам) и из любой точки можно в любую

другую пройти ребрам, причем единственным способом

––

получилось де

рево. Докажите, что ребер в дереве n −1 и число различных деревьев

равно n

n−2

(теорема Кэли **).

У к а з а н и е. Выбрать висячую, т. е. являющуюся концом лишь одно

го ребра, вершину с наименьшим номером, написать номер второго конца

этого ребра, выбросить из дерева это ребро, с оставшимся деревом сде

лать то же самое и т. д., потом показать, что получившаяся в результате

* О программе поиска новых простых чисел Мерсенна совместными усилиями пользо

вателей Интернета см.

** А. Кэли (Arthur Cayley, 1821

–

1895)

––

английский математик. Работая адвокатом в те

чение 14 лет, опубликовал около 250 математических работ. Оставив адвокатскую практику

в 1863 г., стал профессором математики в Кембриджском университете.

§ 1.7. Полиномиальная теорема 45

последовательность длины n −2 чисел из множества {1, . . ., n} однознач

но определяет исходное дерево.

§ 1.7. Полиномиальная теорема

Обозначим через I(A, B) множество всех вложений f : A →B. Други

ми словами, это число размещений элементов множества A по ящикам,

являющимся элементами множества B.

Ясно, что I(A, B) не пусто тогда и только тогда, когда |A|6 |B|.

Определение 20. Число V · (V −1) ·. . . · (V − n + 1) называется

убывающим факториалом числа V длины n и обозначается [V]

Число V · (V + 1) ·... · (V + n −1) называется возрастающим фак-

ториалом числа V длины n и обозначается [V]

Упражнение 15. Докажите, что [−V]

= (−1)

[V]

, [−V]

= (−1)

[V]

Теорема 12 (о числе размещений). Справедливо равенство

|I(A, B)|= |B|· (|B|− 1) · . .. · (|B| −|A|+ 1) = [|B|]

|A|

Д о к а з а т е л ь с т в о. Индукция по |A|. База (|A|= 1) очевидна.

Шаг индукции. Пусть A = {1, 2, .. ., n}, B = {1, 2, ..., m}. Любое отоб

ражение f , принадлежащее множеству I(A, B), однозначно определяется,

если задать значение f(n) = i из B и отображение f

, принадлежащее

множеству I(A

, B

), где A

= {1, 2, ..., n −1} и B

= B \{i}. Таким обра

зом, построено взаимно однозначное отображение из множества I(A, B)

в множество

[

i=1

I(A

, B

) × {i}.

Из предположения индукции и теоремы 9 теперь следует, что

|I(A, B)|= m · (m −1) ·. . . · (m −n + 1).

Определение 21. Факториалом числа V ∈N называется произве

дение V ! = V · (V −1) · (V − 2) · . .. ·2 ·1. Для V = 0 полагаем 0! = 1.

Тогда [V]

= V !

(V −n)! при V > n > 0.

Теорема 13 (о числе перестановок). Справедливо равенство

|I(A, A)|= |A| · (|A| −1) ·... · 1 = |A|!

Д о к а з а т е л ь с т в о. Утверждение является частным случаем тео

ремы 12.

Для краткости вместо I(A, A) пишем S(A).

46 Глава I. Числа и комбинаторика

Определение 22. Элементы множества S(A) называются переста-

новками множества A.

Определение 23. Перестановкой с повторениями называется

любое слово из множества {1, ..., k}

, в котором каждая

буква

встречается n

раз, где n

+ ... + n

= n.

Множество всех таких слов обозначим S(n

, ..., n

Если имеется n букв (k=n), и каждая буква встречается один раз

=1, i=1, ..., n), то S(1, . . ., 1)

––

это просто множество S({1, 2, ..., n}),

элементы которого записаны в виде слова (a

, ..., a

), принадлежащего

множеству {1, ..., n}

Теорема 14 (о перестановках с повторениями). В обозначениях

определения 23 справедливо равенство

|S(n

, ..., n

)|=

! ... n

Д о к а з а т е л ь с т в о. Сопоставим каждому слову w из S(n

, ..., n

)

множество всех перестановок из S

= S({1, 2, ..., n}), которые получа

ются, если все вхождения каждой буквы i заменить произвольным об

разом на различные числа из множества {l

, l

+ 1, ..., l

+ n

−1}, где

= n

+ ... + n

i−1

. Полученное множество обозначим S

n,w

Из теоремы 8 и теоремы 13 вытекает, что |S

n,w

|= n

! ... n

!. Ясно, что

[

w∈S(n

,. . .,n

)

n,w

––

объединение всех множеств S

n,w

, которые попарно не пересекаются,

т. е. не имеют общих элементов. Поэтому согласно теореме 9

n! = |S

|= |S(n

, ..., n

)|, откуда |S(n

, ..., n

)|=

! ... n

Упражнение 16. а) Сколько различных слов можно получить, пере

ставляя буквы в слове МАТЕМАТИКА?

б) Сколько различных слов можно получить, переставляя буквы

в слове АБРАКАДАБРА?

Перестановка букв в слове называется анаграммой.

Упражнение 17. В XVII в. среди ученых существовал обычай объ

являть о своих открытиях, нуждающихся в подтверждении, публикацией

анаграммы. Галилей, увидев в свою подзорную трубу, что Сатурн имеет

по краям какие

то придатки, опубликовал анаграмму

SMAISMRMIELMEPOETALEUMIBUVNEUGTTAVIRAS.

§ 1.7. Полиномиальная теорема 47

Сколько различных перестановок пришлось бы перепробовать Кеплеру,

чтобы разгадать анаграмму Галилея? Напишите точную формулу и оце

ните число десятичных цифр в изображаемом ею числе.

Из теоремы 14 следует

Теорема 15 (полиномиальная). Справедливо тождество

+ ... + x

)

+. . .+n

! ... n

... x

Д о к а з а т е л ь с т в о. Основной алфавит

––

, ..., x

}. Буква x

входит ровно n

раз в каждое слово, дающее одночлен x

... x

Определение 24. Число

! ... n

обозначается

„

, ... , n

и на

зывается полиномиальным коэффициентом.

Если k = 2, то вместо

„

, n

пишут

„

, ибо n

= n −n

, и назы

вают это число биномиальным коэффициентом. Вместо

“

”

исполь

зуют обычно обозначение C

Упражнение 18.

а) Проверьте, что C

= [n]

k!.

б) Проверьте, что справедливо тождество (двойственность биноми

альных коэффициентов)

n(n −1) ... (n −k + 1)

= C

n−k

в) Докажите, что последовательность C

, C

, ..., C

возрастает вплоть

до коэффициента C

, а с коэффициента C

2]+1

убывает.

г) Докажите чисто алгебраически тождество Паскаля

n+1

= C

+ C

k−1

Частным случаем полиномиальной теоремы является

Теорема 16 (биномиальная). Справедливо тождество

(x + y)

k=0

n−k

Д о к а з а т е л ь с т в о. В полиномиальной теореме положим k=2. 

48 Глава I. Числа и комбинаторика

Определение 25. Треугольником Паскаля называется таблица

1 1

1 2 1

1 3 3 1

. . . . . . . . . . . ,

в которой каждая очередная строка на одно число длиннее предыдущей,

начинается и заканчивается единицей и каждое из остальных ее чисел

равно сумме двух чисел предыдущей строки, между которыми оно нахо

дится.

Теорема 17 (о треугольнике Паскаля). В n-й строке треуголь-

ника Паскаля стоят в точности биномиальные коэффициенты

, C

, ..., C

Д о к а з а т е л ь с т в о. Доказательство проводится по индукции. Ба

за индукции (n = 1) очевидна. Согласно предположению индукции n

строка треугольника Паскаля состоит из чисел C

, C

, .. ., C

. Тогда меж

ду числами C

k−1

, C

в (n + 1)

й строке будет стоять согласно тождеству

Паскаля число C

n+1

= C

k−1

+ C

Задачи и упражнения к § 1.7

1. Кеплер нашел такое решение анаграммы Галилея (опустив две

буквы):

SALVE UMBISTINEUM GEMINAUM MARTIA PROLES

(привет вам, близнецы, Марса порожденье). Он думал, что Галилей от

крыл спутники Марса. На самом деле они были открыты спустя два

века. В действительности Галилей зашифровал фразу (тоже выбросив две

буквы)

ALTISSIMUM PLANETAM TERGEMINUM OBSERVAVI

(высочайшую планету тройною наблюдал). Но он ошибся. Вместо при

датков у Сатурна оказалось кольцо, которое открыл позднее Гюйгенс.

Об этом он тоже опубликовал анаграмму

AAAAAAACCCCCDEEEEGHIIIIIIILLLLMMMNNNNNNNNNOO

OOPPQRRSTTTTTUUUU.

§ 1.7. Полиномиальная теорема 49

Сколько различных перестановок пришлось бы перепробовать, чтобы

разгадать анаграмму Гюйгенса? Напишите точную формулу и оцените

число десятичных цифр в изображаемом ею числе.

2. Докажите биномиальную теорему по индукции.

3. Выведите из нее полиномиальную теорему.

4. Если множества A

попарно не пересекаются и

∪... ∪A

|> k

+ ... + k

−n + 1,

то |A

|> k

для некоторого i (принцип Дирихле).

5. Если (n, 10) = 1, то из одних единиц можно составить число 11.. .1,

делящееся на n.

6*. Существует число, делящееся на 2

, десятичная запись которого

состоит только из 1 и 2.

7*. Существует число, делящееся на 5

, десятичная запись которого

состоит только из цифр 1, 2, 3, 4, 5.

8*. Если (n, 5) = 1, то существует число, делящееся на n, десятичная

запись которого состоит только из цифр 1, 2.

9*. Если (n, 2) = 1, то существует число, делящееся на n, десятичная

запись которого состоит только из цифр а) 1, 2, 3, 4, 5; б) 5, 6, 7, 8, 9;

в) только из нечетных цифр.

10*. (С. В. Конягин.) Докажите, что для любого n найдется число, все

цифры которого в десятичной записи равны 0, 1, 8, 9, не превосходящее n

и делящееся на n.

11. Сколькими способами можно расставить n ладей на шахматной

доске n ×n так, чтобы они не били друг друга?

12. Сколькими способами можно разместить n одинаковых шаров

по m урнам так, чтобы в каждой урне оказалось не более одного шара?

13. Докажите тождество

+ . . . +n

„

, ... , n

= k

14. Выведите из полиномиальной теоремы, что при простом p и лю

бом натуральном k число k

−k делится на p (малая теорема Ферма).

15. Если p

––

простое, большее 5, то число 11...1, десятичная запись

которого состоит из p −1 единицы, делится на p.

16. В классе для каждого k = 1, ..., n ровно a

учеников получили

не менее k двоек. Сколько всего двоек в этом классе?

4 Гашков

50 Глава I. Числа и комбинаторика

17. (Лежандр *.) a) Докажите, что простое число p входит в разло

жение n! в степени

+ ... +

, где p

6 n < p

k+1

б) Докажите, что

+ ... +

+ ... =

n −ν

(n)

p −1

где ν

(n)

––

сумма цифр p

ичной позиционной записи числа n.

в) Пусть

= (p

k+1

−1)

(p − 1),

h = p

+ ... + p

+ p

, p

= ⌊h

⌋,

m−1

= h − p

, p

m−1

= ⌊h

m−1

⌋,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

= h

− p

, p

= ⌊h

⌋.

Тогда простое p входит в разложение n! в степени h тогда и только тогда,

когда

n = p

m+1

+ ... + p

+ p

p + p

′

где все p

и p

′

суть целые неотрицательные и меньше p.

18. Может ли n! оканчиваться ровно 2004 нулями в десятичной

записи?

19. При каких n число (n −1)!

––

целое?

20. Докажите, что число (2n)!

(n!)

натуральное и делится на n + 1.

21. Докажите, что

a! b! .. . k!

––

целое, если a + b + .. . + k 6 n.

22. Докажите, что число (2n)!

(n!)

натуральное и делится на n + 1

и на 2

(n)

, но не делится на 2

(n)+1

23. Докажите, что число (2n)!

n! делится на 2

, но не на 2

n+1

24. Докажите, что число n!

––

нецелое. При каком натуральном m

число n!

n−m

будет целым при всех натуральных n?

25**. (Чебышёв **.) Выведите из предыдущей задачи, что число

√

не больше произведения по всем простым делителям p числа n сомножи

телей p

(p−1)

, и выведите отсюда, что простых чисел бесконечно много.

* А. М. Лежандр (Adrien Marie Legendre, 1752

–

1833)

––

известный французский мате

матик.

** Чебышёв Пафнутий Львович (1821

–

1894)

––

выдающийся русский математик, созда

тель петербургской математической школы.