Galdi G.P. An Introduction to the Mathematical Theory of the Navier-Stokes Equations: Steady-State Problems
Подождите немного. Документ загружается.

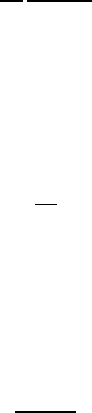
436 VII Steady Oseen Fl ow in Exterior Domains
estimates for E(x −y) as a function of y for fixed x. Considered as a function
of x, all estimates remain true if ϕ is replaced by π − ϕ, see Remark VII.3.1.
Taking x as the origin of coordinates (this produces no loss of generality since
E is a function of x − y only) and noticing that
e
−s
≤ (1 −e
−s
)/s, s > 0, |(y
j
− x
j
)/s| ≤ 2/λ, j = 2, 3 ,
from (VII.3.20) we o bta in
|E(y)| ≤
c
1
|y|
1 − e
−s
s
, (VII.3.23)
where c
1
= c
1
(λ) and
s = λ(|y| −y
1
) = λ|y|(1 −cos ϕ).
The bound (VII.3.23) f urnishes, in particular, the uniform estimate
|E(y)| ≤
c
1
|y|
, (VII.3.24 )
which coincides with tha t given for U in (IV.2.6). However, improved bounds
can b e derived from (VII.3 .23) as a function of ϕ. Specifically, if
(1 − cos ϕ) ≥ |y|
−1+2σ
for some σ ∈ [0, 1/2], (VII.3.25)
then (VII.3.23) implies
|E(y)| ≤
c
2
|y|
1+2σ
, (VII.3.26 )
with c
2
= c
2
(λ). From (VII.3.23)–(VII.3.26) it follows tha t if y belongs to the
region defined by
|y|(1 − cos ϕ) ≤ 1 (VII.3.27)
then (VII.3.24) holds. This region represents a parabo loid with the axis in the
direction of the negative x
1
-axis and can be interpreted as a “wake.”
Remark VI I.3.1 The tensor E(x − y) considered as a function of y thus
exhibits a “wake” region in the direction opposite to what is expected for a
body moving in a liquid with the velocity v
0
directed in the positive x
1
-axis
(as we have assumed at the beginning of the chapter). This is due to the fact
that, as a function of y, E satisfies the adjoint system (VII.3.18). However,
if we consider E as a function of x, then ϕ should be changed in π − ϕ and
the parabolo idal wake region becomes appropriately located with its axis in
the direction of the negative x
1
-axis. This remark is important in the context
of the a symptotic structure of solutions to the Oseen system; see Theorem
VII.6.2 and Remark VII.6.1.

VII.3 The Oseen Fundament al Solution 437
Starting from (VII.3.23) we may also derive the summability properties
of E(y) in the exterior A of a ball of unit (say) radius. In particular, by a
straightforward calculation we show
E(y) ∈ L
q
(A) for all q > 2. (VII.3.28)
This estimate is sharp; a ctual ly, from (VII.3 .20)
1
we have with a = 1/λr
|E
11
(y)| =
1
8πr
|e
−s
[1 + (1 − a) cos ϕ] + a cos ϕ|
Thus, for all r ≥ λ and all ϕ ∈ [0, π/2], we find
|E
11
(y)| ≥
1
8πr
e
−λr(1−cos ϕ)
.
From this relation it follows tha t
kE
11
k
q
q,A
≥ c
Z
∞
λ
r
−q+2
e
−λqr
Z
π/2
0
e
λqr cos ϕ
sin ϕ dϕ
!
dr
= c
Z
∞
λ
r
−q+2
e
−λqr
Z
1
0
e
λqrx
dx
dr
= c
1
Z
∞
λ
r
−q+1
(1 −e
−λqr
) dr .
(VII.3.2 9)
Therefore, setting
R = max
λ, −
1
λq
ln
1
2
,
from (VII.3.29) we o bta in
kE
11
k
q
q,A
≥ c
1
Z
∞
R
r
−q+1
dr,
showing that E
11
does not belong to L
q
(A) fo r all q ∈ [1, 2 ]. A similar con-
clusion can be reached for the other components of E, by means of the same
technique, which allows us to conclude
E(y) 6∈ L
q
(A), for all q ∈ [1, 2]. (VII.3.30)
The summability properties (VII.3.28), (VII. 3.30) should be contrasted with
the analogous properties of the Stokes fundamental tensor U, for which (in
dimension 3) we have that U belongs to L
q
(A) for all and only all q > 3.
Estimates similar to (VI I.3.23) can be derived for first derivatives. Specif-
ically, from (VII.3.20) the following inequalities are directly obtained
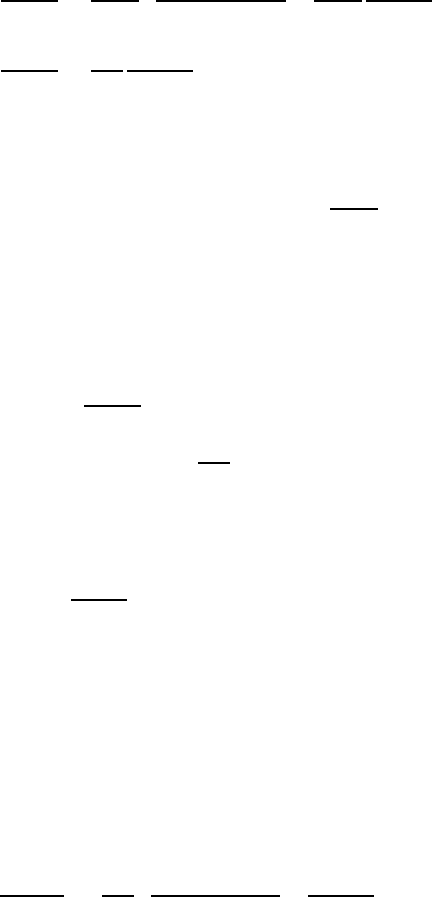
438 VII Steady Oseen Fl ow in Exterior Domains
∂E(y)
∂y
i
≤
c
|y|
3/2
1 − e
−s
− se
−s
s
3/2
+
1
|y|
1/2
1 − e
−s
s
, i = 2, 3
∂E(y)
∂y
1
≤
c
|y|
2
1 − e
−s
s
(VII.3.3 1)
with c = c(λ). These formulas imply, in particular, the uniform bound for |y|
greater than any fixed R
0
> 0:
|∇E(y)| ≤
c
1
|y|
3/2
(VII.3.3 2)
with c
1
= c
1
(λ, R
0
). However, better estimates can be derived outside the
“wake region” (VII. 3.27), in a way completely analog ous to that used previ-
ously, and we leave them to the reader a s an exercise. Concerning the summa-
bility of ∇E in a neighborhood of infinity, we notice that by (VII.3.31) we
have
∂E(y)
∂y
i
∈ L
q
(A), for all q > 4/3, i = 2, 3
∂E
∂y
1
∈ L
q
(A), for all q > 1,
(VII.3.3 3)
where A, as before, denotes the exterior of a uni t ball. Condition (VII.3.33)
1
is sharp in the sense that
∂E(y)
∂y
i
6∈ L
q
(A), for all q ∈ [1, 4/3], i = 2, 3 (VII. 3.34)
as a result o f a calculation similar to that used to show (VII.3.30). It is inter-
esting to observe that, even though the unif orm bo und (VII.3.32) is weaker
than the analogous one for the Stokes fundamental tensor U (see (IV. 2.6)),
the summability properties (VII.3.33) are stronger than those for U , where
(in dimension 3) ∇U ∈ L
q
(A) for a ll and only all q > 3/2.
Further estima tes can be obtained for derivatives of order higher than one.
Here, we shall limit ourselves to presenting some bounds of particula r interest,
leaving their proofs to the reader.
∂
2
E(y)
∂y
i
∂y
j
≤
c
|y|
2
1 − e
−s
−se
−s
4s
2
|y|
+
1 − e
−s
2s
, y ∈ R
3
− {0}
|D
α
E(y)| ≤ c|y|
−1−|α|/2
, |α| ≥ 2 , sufficiently large |y|.
(VII.3.3 5)
Exercise VII.3.1 Show that (in three dimensions) the tensor E satisfies the fol-
lowing estimates for all R > 0:
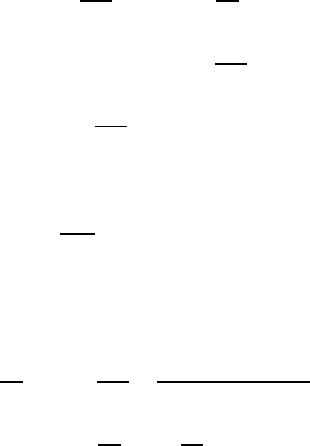
VII.3 The Oseen Fundament al Solution 439
Z
∂B
R
|E(y)|
2
≤ cR
−1
,
Z
∂B
R
|∇E( y)| ≤ cR
−1/2
,
Z
∂B
R
|∇∇E(y)| ≤ cR
−1
.
Hint: Use estimates (VII.3.23), (VII.3.33), and (VII.3.35); see also Solonnikov (1996).
We next derive the form and corresponding estimates for E(x −y) in two
space dimensions. From (VII.3.1) and (VII.3.16) we find
E
11
(x − y) =
∂
∂y
1
Ψ(x −y) −
1
2π
K
0
(λ|x − y|)e
−λ(x
1
−y
1
)
E
12
(x − y) = E
21
(x − y) = −
∂
∂y
2
Ψ(x − y)
E
22
(x − y) = −
∂
∂y
1
Ψ(x − y)
where
Ψ(x − y) =
1
4πλ
log |x − y| + K
0
(λ|x − y|)e
−λ(x
1
−y
1
)
.
From (VII.3.16) and the properties (VI I.3.10) of the f unction K
0
(z) near z =
0, we easily obtain, with r = |x − y|
E
ij
=−
1
4π
δ
ij
log
1
2λr
+
(x
i
− y
i
)(x
j
− y
j
)
r
2
+ o(1)
=U
ij
(x − y) −
1
4π
δ
ij
log
1
2λ
+ o(1), as λr → 0,
(VII.3.3 6)
where U is the Stokes fundamental tensor (IV.2.4). Using (VII.3.36) and
(VII.3.1 7), we then show the validity of (VII.3.22 ) also in two dimensions.
It shoul d be observed that, unlike the three-dimensional case (see (VII.3.21)),
relation (VII.3.36) for arbitrarily fixed x, y becomes singular as λ → 0. This
is to be expected f or, as we are going to show, the tensor E vanishes at l arge
spatial distances, while U grows there logarithmically. Denote by ϕ the angle
made by a ray that starts from x and is directed toward y, with the direction
of the positive x
1
-axis. From (VII.3.1), (VII.3.15) and (VII.3.16) we derive in
the limit λr → ∞

440 VII Steady Oseen Fl ow in Exterior Domains
E
11
(x − y) = −
cos ϕ
4πλr
+
e
−s
4
√
2λπr
1 + cos ϕ −
1 − 3 cos ϕ
8λr
+ R(λr)
E
12
(x − y) = E
21
(x − y) =
sin ϕ
4πλr
−
e
−s
sin ϕ
4
√
2λπr
1 +
3
8λr
+ R(λr)
E
22
(x − y) =
cos ϕ
4πλr
+
e
−s
4
√
2π(λr)
3/2
s −
1 + 3 cos ϕ
8
+ R(λr)
,
(VII.3.3 7)
where
s = λr(1 −cos ϕ)
and the remainder R(t) satisfies
d
k
R
dt
k
= O(t
−2−k
), as t → ∞ , k ≥ 0.
From (VII.3.37 ) it follows that unlike the Stokes fundamental tensor, which
grows logari thmically rapid for r → ∞, the Oseen fundamental tensor van-
ishes at large distances. It is this difference that al lowed Oseen to remove
the discrepancy generating the Stokes paradox. Relations (VII.3.37) produce
some useful estimates. We shall present them as a function of y, fixing the
origin of coordinates at x = 0. Analogous estimates of E as a function of x
remain true if ϕ is replaced by π −ϕ, and the considerations m ade in Remark
VII.3.1 apply here.
From (VII.3.37)
1
it readily follows that E
11
(y) exhibits the same parabolic
“wake” region that was obtained in the three-dimensional case. In fact, if y is
interior to the parabola
2
|y|(1 − cos ϕ) = 1
we deduce the uniform bound
|E
11
(y)| ≤
c
|y|
1/2
, as |y| → ∞, (VII.3.38)
while if
(1 − cos ϕ) ≥ |y|
−1+2σ
for some σ ∈ [0, 1/2] (VII.3.39 )
we have
|E
11
(y)| ≤
c
|y|
1/2+σ
, as |y| → ∞. (VII.3.40)
However, unlike the three-dimensional case, the remaining components of E
do not present such a nonuniform behavior. In fact, observing that
2
Setting θ = π −ϕ, the parabolic region can be approximately described, for large
|y|, by
|θ| ≤ (2)
1/2
|y|
−1/2
.
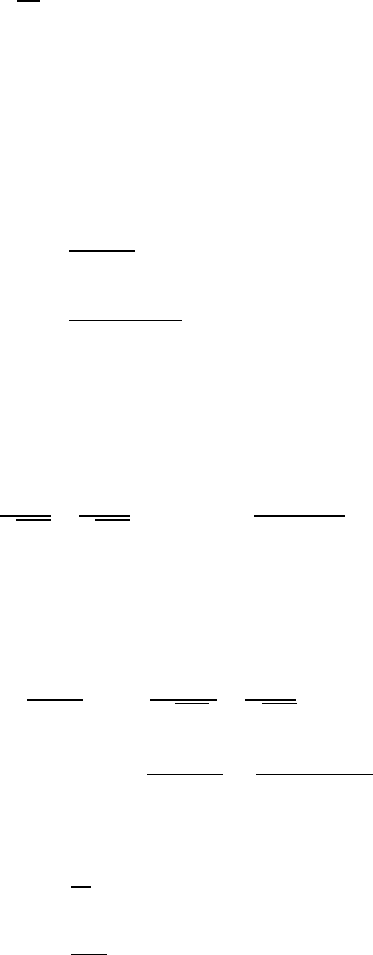
VII.3 The Oseen Fundament al Solution 441
e
−2s
λr sin
2
ϕ = se
−2s
(1 + cos ϕ) ≤ e
−1
from (VII.3.37)
2,3
we recover the uniform estimates
|E
i2
(y)| ≤
c
|y|
, i = 1 , 2, as |y| → ∞. (VII.3.41)
Concerning the summability properties of E, denoting by A the exterior
of a unit circle, from (VII.3.41) we recover at once
E
i2
(y) ∈ L
q
(A), for all q > 2, i = 1, 2. (VII.3.42)
Moreover, setting cos ϕ = ∓(y − λqr)/λqr, where “−” is taken if ϕ ∈ [0, π]
and “+” otherwise, by a direct calculation one shows for any q ≥ 1
Z
2π
0
e
−qs
(1 + cos ϕ)
q
dϕ ≤
2
(4λqr)
q
Z
2λqr
0
e
−y
(2λqr − y)
q−1/2
y
−1/2
dy
≤
2(4λqr)
q−1/2
(2λqr)
q
Z
∞
0
e
−y
y
−1/2
dy = c
1
/r
1/2
,
with c
1
independent of r. As a consequence, from (VII.3.37)
1
we obtain
E
11
(y) ∈ L
q
(A), for all q > 3. (VII.3.43)
Likewise, setting
f(ϕ, r) ≡ −
cos ϕ
√
πλr
+
e
−s
√
2λπ
1 + cos ϕ −
1 − 3 cos ϕ
8λr
one has
Z
2π
0
|f(ϕ, r)|
q
dϕ ≥
Z
π
0
|f(ϕ, r)|
q
dϕ
=
1
(λqr)
q
Z
2λqr
0
y − λqr
√
λπr
+
e
−y/q
√
2λπ
2λqr − y
−
3y −λqr
8λqr
q
y
−1/2
(2λqr −y)
1/2
dy,
and so, for all r sufficiently large
Z
2π
0
|f(ϕ, r)|
q
dϕ ≥
c
1
r
q
Z
1
0
e
−y
(2λqr − y)
q−1/2
y
−1/2
dy
≥
c
2
r
1/2
Z
1
0
e
−y
y
−1/2
dy = c
3
/r
1/2
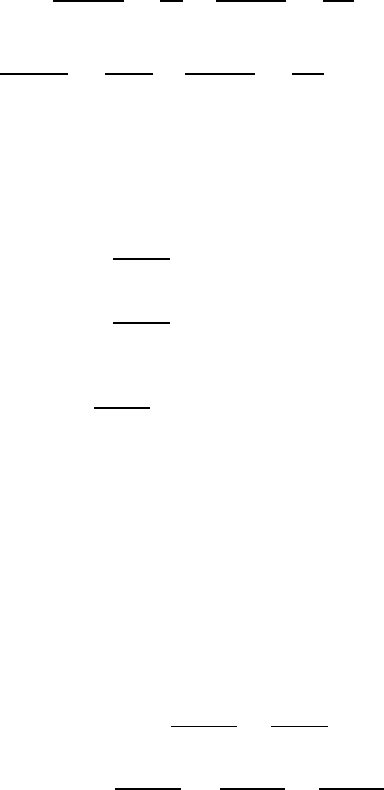
442 VII Steady Oseen Fl ow in Exterior Domains
with c
3
independent of r, and from (VII.3 .37)
1
it follows that
E
11
(y) 6∈ L
q
(A), for all q ∈ [1, 3]. (VII.3.44)
So far as the behavior of the first derivatives of E is concerned, differentiating
(VII.3.3 7) we derive the fo llowing bounds as |y| → ∞
∂E
11
(y)
∂y
2
≤
c
|y|
,
∂E
12
(y)
∂y
1
≤
c
|y|
2
,
∂E
1i
(y)
∂y
i
≤
c
|y|
3/2
,
∂E
22
(y)
∂y
i
≤
c
|y|
2
, i = 1, 2.
(VII.3.4 5)
Sharper estimates can be obtained for the derivatives of E
11
and the deriva-
tive of E
12
with respect to y
2
whenever y is exterior to the “wake” region,
see Exercise VII.3.2. Mo reover, besides the obvious summability properties
obtainable from (VII.3.45) one can show (Exercise VII.3.2)
∂E(y)
∂y
1
∈ L
q
(A) for all q > 1
∂E(y)
∂y
2
∈ L
q
(A) for all q > 3/2
(VII.3.4 6)
while
∂E(y)
∂y
2
6∈ L
q
(A) for all q ∈ [1, 3/2]. (VII.3.47)
Further asymptotic bounds can be analogously derived for derivatives of
order higher than two. For instance, one shows the validity of the fol lowing
properties (see Exercise VII.3. 3):
D
2
E(y) ∈ L
q
(A), for all q > 1,
|D
α
E(y)| ≤ c|y|
−(1+|α|) /2
, |α| ≥ 2, as |x| → ∞.
(VII.3.4 8)
Exercise VII.3.2 Let E be given as in ( VII.3.37). Show that for all σ ∈ [0, 1/2]
and all sufficiently large |y|,
˛
˛
˛
˛
∂E
11
(y)
∂y
2
˛
˛
˛
˛
≤
c
|y|
1+2σ
˛
˛
˛
˛
∂E
11
(y)
∂y
1
˛
˛
˛
˛
,
˛
˛
˛
˛
∂E
12
(y)
∂y
2
˛
˛
˛
˛
≤
c
|y|
3/2+σ
in region (VII.3.39). Furthermore, show the validity of (VII.3.46) and (VII.3.47).
Exercise VII.3.3 Show estimate (VII.3.48).
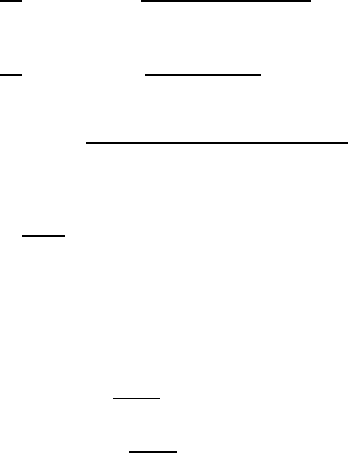
VII.3 The Oseen Fundament al Solution 443
Exercise VII.3.4 Prove that (in two dimensions) the tensor E obeys the following
estimates for all R > 0:
Z
∂B
R
|E(y)|
2
,
Z
∂B
R
|∇E(y)| ≤ cR
−1/2
.
Hint: Use (VII.3.39) and (VII.3.41).
Exercise VII.3.5 Let E(x − y) ≡ E(x − y; 2λ) denote the Oseen tensor corre-
sponding to 2λ. Show the following homogeneity properties
E(x − y; 2λ) = 2λE(2λ(x − y); 1) for n = 3,
E(x − y; 2λ) = E(2λ(x − y); 1) for n = 2.
Remark VI I.3.2 Estimates a nalog ous to those presented for space dimen-
sion n = 2, 3 can be derived for al l n ≥ 4. Actually, from (VII.3.10)
2
and
(VII.3.1 1) it follows that the n-dimensional Oseen fundamental tensor E(x−y)
(defined by (VII. 3.1), (VII.3.4), and (VII.3. 8)) sati sfies (VII.3.21) and, conse-
quently, becomes singular at x = y in such a way that (VII.3.22) is verified.
Furthermore, using the asymptotic expansion for large z:
K
(n−2)/2
=
π
2z
1/2
e
−z
"
ν−1
X
k=0
Γ (n/2 + k −1/2)
k!Γ (n/2 − k −1/2)
(2z)
−k
+ σ
ν
(z)
#
=
π
2z
1/2
e
−z
1 +
4(n −2)
2
− 1
8z
+
[4(n − 2)
2
−1] [4(n − 2)
2
− 3
2
]
2!(8z)
2
+ . . . + σ
ν
(z)
with
d
k
σ
ν
dz
k
= O(z
−k−ν
) as z → ∞, k ≥ 0,
see Watson (1962, p. 202 ), one can obtain estimates at large distances. For
instance, we can show
|D
α
E(y)| ≤ c|y|
−(n−1+|α|)/2
, |y| → ∞, |α| ≥ 0,
E(y) ∈ L
q
(A), q >
n + 1
n − 1
∇E(y) ∈ L
r
(A), r >
n + 1
n
D
2
E(y) ∈ L
s
(A), s > 1.
(VII.3.4 9)

444 VII Steady Oseen Fl ow in Exterior Domains
In analogy with what we did for the Stokes problem, we now introduce
the Oseen volume potentials:
u(x) = 2λ
Z
R
n
E(x − y) · F (y)dy
π(x) = −2λ
Z
R
n
e(x − y) · F (y)dy,
(VII.3.5 0)
where F ∈ C
∞
0
(R
n
). Since
Z
R
n
E(x − y) · F (y)dy =
Z
R
n
E(z) · F (x + z)dz,
one has u ∈ C
∞
(R
n
) and, by the same token, π ∈ C
∞
(R
n
). Moreover, it is
easy to show that u, π satisfy the Oseen system in R
n
. Actually, it is obvious
that ∇· u = 0. Also, using integration by parts and (VII.3.2) we deduce for
all x ∈ R
n
∆u(x) + 2λ
∂u(x)
∂x
1
−∇π = ∆(E ∗ F ) = 2λF (x).
Moreover, it is easy to show that the solution u, π behaves at large distances
exactly as the fundamental solution E, e. This immediately follows by ob-
serving that from (VII.3.49) we have
u(x) = 2λE(x) ·
Z
R
n
F (y)dy + σ(x)
π(x) = −2λe(x) ·
Z
R
n
F (y)dy + η(x)
(VII.3.5 1)
with
σ(x) = 2λ
Z
R
n
(E(x −y) − E(x)) · F (y)dy
π(x) = −2λ
Z
R
n
(e(x −y) − e(x)) · F (y)dy
and that, using the mean-value theorem and the assumption F ∈ C
∞
0
(R
n
),
D
α
σ(x) = O(D
α
∇E(x))
D
α
η(x) = O(D
α
∇e(x))
|α| ≥ 0, |x| → ∞. (VII.3 .52)
Remark VI I.3.3 Starting with (VII.3.50)
1
and using Young’s theorem on
convolution (see Theorem II.11.1) one can prove at once L
q
-estimates for u, π
and their first derivatives. This is due to the circumstance that, unlike the
Stokes tensor U , the Oseen tensor possesses global summability properties in
the whole of R
n
. For instance, from (VII.3.49) and (VII.3.21) we see tha t

VII.4 Existence, Uniqueness, and L
q
-Estimates in the Whole Space 445
E(y) ∈ L
q
(R
n
) f or all q ∈ ((n + 1)/(n − 1), n) if n > 2,
E(y) ∈ L
q
(R
n
) f or all q ∈ (3, ∞) if n = 2.
However, estima tes obtained in such a way would not be sharp and, therefore,
we shall not derive them here. Derivation of sharp estimates for the Oseen
potentials, by different tools, will be the object of the next section.
VII.4 Existence, Uniqueness, and L
q
-Esti mates in the
Whole Space
The objective of this section is to prove existence, uniqueness, and correspond-
ing estimates of solutions v, p to the nonhomogeneous O s een syst em
∆v + R
∂v
∂x
1
−∇p = Rf
∇ · v = g
in R
n
(VII.4.1 )
in homogeneous Sobolev spaces D
m,q
(R
n
). These results, though sharing some
similarity with the analogous ones established for the Stokes system in Chap-
ter IV, wi ll differ from these latter in some crucial f eatures that essentially
mirror the basic differences existing between the two fundamental tensors U
and E.
In establishing estimates for (VII.4.1), it is important to single out the
dependence of the constants entering the estimates on the dimensionless pa-
rameter R. We shall therefore consider the problem
∆v +
∂v
∂x
1
−∇p = f
∇ · v = g
in R
n
(VII.4.2 )
and establish corresponding estimates for i ts solutions. The analogous ones
for solutions to (VII.4.1) will then be obtained if we make the replacements
f → f/R
g → g/R
p → p/R
x
i
→ Rx
i
.
(VII.4.3 )
Unlike the corresponding estimates for the Stokes system, here we cannot
employ the Calder´on–Zygmund theorem because the kernel D
2
ij
E
ks
(x − y)
does not satisfy the assumption (II.11.15) of that theorem, that is,
α
−n
D
2
ij
E
ks
(ξ) 6= D
2
ij
E
ks
(αξ), α > 0.
