Galdi G.P. An Introduction to the Mathematical Theory of the Navier-Stokes Equations: Steady-State Problems
Подождите немного. Документ загружается.

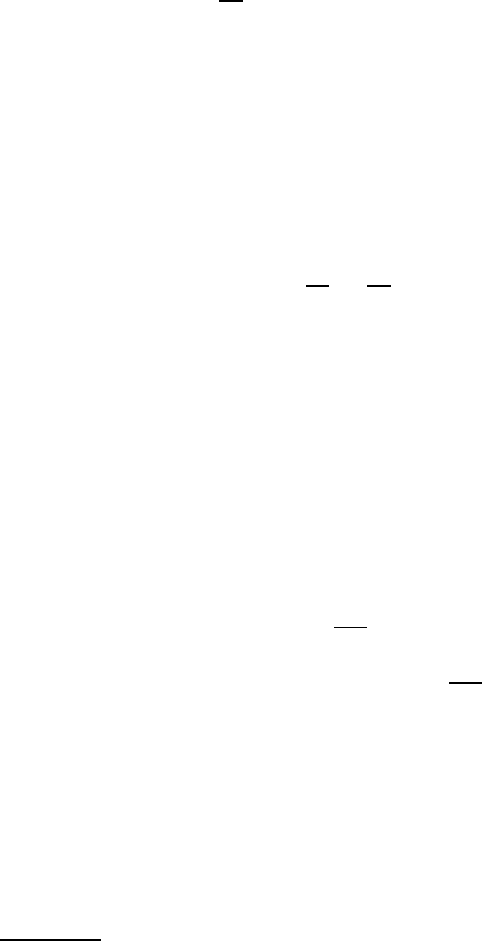
426 VII Steady Oseen Fl ow in Exterior Domains
there exists one and only one generalized solutio n to (VII.0.2), (VII.0.3). This
solution satisfies the estimates
1
kvk
2,Ω
R
+ |v|
1,2
≤ c
1
R|f|
−1,2
+ (1 + R)kv
∗
k
1/2,2(∂Ω)
Z
S
2
|v(x)| = o(1/
p
|x|) as |x| → ∞
kpk
2,Ω
R
/ R
≤ c
2
{R|f|
−1,2
+ (1 + R)|v|
1,2
}
(VII.2.1 )
for all R > δ(Ω
c
). In (VII.2.1) p is the pressure field associated to v by Lemma
VII.1.1, while c
i
= c
i
(R, Ω) (c
i
→ ∞ as R → ∞).
Proof. We look for a solution of the form
v = w + V
1
+ σ, (VII.2.2)
where
σ =
Φ
4π
∇
1
|x|
Φ =
Z
∂Ω
v
∗
· n
(the origin of coordinates has been taken in
˙
Ω
c
). Further, V
1
∈ W
1,2
(Ω)
denotes the solenoidal extension of v
∗
−σ|
∂Ω
, of bounded support in Ω, that
was constructed in the proof of Theorem V.1.1. We have
|V
1
|
1,2
≤ c kv
∗
k
1/2,2(∂Ω)
D
α
σ = O(1 /|x|
2+|α|
) , |α| = 0, 1, as |x| → ∞.
(VII.2.3 )
Finally, w is requested to be a member of D
1,2
0
(Ω) and to satisfy the identity
(∇w, ∇ϕ) −R(
∂w
∂x
1
, ϕ)
= −R[f , ϕ] − (∇V
1
, ∇ϕ) + R(V
1
+ σ,
∂ϕ
∂x
1
),
(VII.2.4 )
for all ϕ ∈ D(Ω). It is clear that, provided we show the existence of such a
function w, the field (VII.2.2) satisfies all requirements of generalized solution
to (VII.0 .2), (VII.0.3) given in Definition VII.1.1. Actually, from (VII.2.3)
2
and the properties of V
1
and w, we have v ∈ D
1,2
(Ω); also, v is divergence-
free and assumes the value v
∗
at the boundary. Finally, in view of (VII.2.3)
2
,
we have, as |x| → ∞,
Z
S
2
|v(x)| ≤
Z
S
2
|w(x)| + O(1/|x|
2
) (VII.2.5)
1
See ( IV.6.1) for the definition of the norm involving p.

VII.2 Existence for Three-Dimensional Flow 427
and by Theorem II.7.6 and Lemma II.6.2 we obtain (VII.2.1)
2
. Thus, to show
the theorem it remains to prove the existence of the field w and the vali dity
of estimates (VII.2.1)
1,3
. To this end, l et {ϕ
k
} be the base of D
1,2
0
(Ω) deter-
mined in Lemma VII.2.1. We shall construct an “approximate solution” w
m
to (VII.2.4) in the following way:
w
m
=
m
X
`=1
ξ
`m
ϕ
`
(∇w
m
, ∇ϕ
k
) − R(w
m
,
∂ϕ
k
∂x
1
)
= −R[f , ϕ
k
] − (∇V
1
, ∇ϕ
k
) − R(V
1
+ σ,
∂ϕ
k
∂x
1
) ≡ F
k
,
k = 1, 2, . . ., m.
(VII.2.6 )
Using (ii) of Lemma VII.2. 1 we obtain
m
X
`=1
(ξ
`m
δ
`k
−Rξ
`m
A
`k
) = F
k
, k = 1, 2, . . ., m (VII.2.7)
where
A
`k
≡ (
∂ϕ
`
∂x
1
, ϕ
k
).
System (VII.2.7) is linear in the unknowns ξ
`m
, ` = 1, . . ., m, and since A
`k
=
−A
k`
it is readily seen that the determinant of the coefficients is non-zero. As
a consequence, f or each m ∈ N, system (VII.2.6) admits a uniquely determined
solution. Let us multi ply (VII.2.6)
2
by ξ
km
and sum over k from 1 to m. We
obtain
|w
m
|
2
1,2
= −R[f , w
m
] − (∇V
1
, ∇w
m
) −R(V
1
+ σ,
∂w
m
∂x
1
). (VII.2.8)
Using (VII.2.3) and recalling that f ∈ D
−1,2
0
(Ω), we easily show
−[f, w
m
] ≤ |f|
−1,2
|w
m
|
1,2
−(∇V
1
, ∇w
m
) ≤ c
1
kv
∗
k
1/2,2(∂Ω)
|w
m
|
1,2
−(V
1
+ σ,
∂w
m
∂x
1
) ≤ c
2
kv
∗
k
1/2,2(∂Ω)
|w
m
|
1,2
and (VII.2.7) furnishes
|w
m
|
1,2
≤ c
R|f|
−1,2
+ (1 + R)kv
∗
k
1/2,2(∂Ω)
. (VII.2.9)
Therefore, the sequence {w
m
} remains uniformly bounded in D
1,2
0
(Ω) and,
by Exercise II.6.2, there exist a subsequence, denoted again by {w
m
}, and a
function w ∈ D
1,2
0
(Ω) such that in the limit m → ∞

428 VII Steady Oseen Fl ow in Exterior Domains
(∇w
m
, ∇ϕ) → (∇w, ∇ϕ), for all ϕ ∈ D
1,2
0
(Ω).
Also, by (VII.2 .9) and Theorem II.2.4 we infer
|w|
1,2
≤ c
R|f|
−1,2
+ (1 + R)kv
∗
k
1/2,2(∂Ω)
(VII.2.1 0)
with c = c(Ω). For fixed k, we then pass to the limit m → ∞ into (VII.2.6)
2
to
deduce wi th no difficulty that v satisfies (VII.1.1) for all ϕ
k
. Since, by Lemma
VII.2.1, every ϕ ∈ D(Ω) can be approximated in the W
1,2
-norm by a linear
combination of ϕ
k
, we establish the validity of (VII.1.1) fo r al l ϕ ∈ D(Ω).
Let us next prove estimates (VII.2.3)
1,3
. We observe that, in view (VII.2.3)
2
,
Theorem II.6.1 and the H¨older inequality, we deduce
kvk
2,Ω
R
≤ |Ω
R
|
1/3
kvk
6,Ω
R
≤ c |Ω
R
|
1/3
|v|
1,2
(VII.2.1 1)
where c = c(Ω), and so, since
|v|
1,2
≤ |w|
1,2
+ |V
1
|
1,2
+ |σ|
1,2
,
inequality (VII.2.1)
1
follows from (VII.2 .10), (VII.2.11), and the properties of
V
1
and σ. Let us finally show (VII.2 .1)
3
. For fixed R > δ(Ω
c
), we add to the
pressure p (defined through L emma VII.1.1) the constant
C(R) = −
1
|Ω
R
|
Z
Ω
R
p
so that
Z
Ω
R
(p + C) = 0.
Successively, we take ψ into (VII.1 .2) as a solution to the problem
∇ψ = p + C in Ω
R
ψ ∈ W
1,2
0
(Ω
R
)
kψk
1,2
≤ c
1
kp + Ck
2,Ω
R
for som e c
1
= c
1
(Ω
R
). This problem is resolvable in virtue of Theorem II.4.1
and so from (VII.1.2) and the Schwarz inequality we have
kp + Ck
2,Ω
R
≤ c
1
(|v|
1,2
+ Rkvk
2,Ω
R
+ R|f |
−1,2
) (VII.2.12)
which, by (VII.2.11), in turn implies (VII.2.1)
3
. The solution v j ust con-
structed is unique in view of Theorem VII.1 .2 a nd therefore the proof of
the theorem is accomplished. ut
Remark VI I.2.1 The methods of Theorem VII.2.1 apply with no change
to show existence of solutions in arbitrary space dimension n ≥ 3 , the only
VII.3 The Oseen Fundament al Solution 429
difference resulting in the asympto tic estimate (VII.2.1)
2
, which has to be
replaced by
Z
S
n
|v(x)| = o(1/|x|
n/2−1
).
If n = 2, by the same technique we can still establish the exi stence of a
vector field v satisfying (i), (ii), (iii), and (v) of Definition VII.1.1, for q = 2;
however, by this technique we are not able to show the validity of condition
(iv) since, as we know, functions in D
1,2
(Ω) for n = 2 need not tend to a
prescribed value at infinity. Nevertheless, unlike the Stokes approximation,
for the problem at hand we can prove existence of generalized solutions by
means of more complicated tools, as will be shown in Theorem VII.5.1.
Remark VI I.2.2 The observations made in Remark V.2.1 apply equally to
the present situation. In particula r, if v
∗
= v
0
+ω×x, for some v
0
, ω ∈ R
3
, the
existence of a generalized solution is proved without regularity assumptions
on Ω.
Exercise VII.2.1 Theorem VII.2.1 can be generalized to the case when ∇·v = g 6≡
0, where g is a suitably prescrib ed function. Specifically, show that for Ω, f and v
∗
satisfying the same assumptions of Theorem VII.2.1 and for all g ∈ L
2
(Ω)∩D
−1,2
0
(Ω)
there exists one and only one generalized solution to the nonhomogeneous Oseen
problem, that is, a field v : Ω → R
n
satisfying (i) (with q = 2), (iii), (iv), and (v)
of Definition VII.1.1 together with ∇ · v = g in the weak sense. Show, in addition,
that, in such a case, estimate (VII.2.1)
1
is modified by adding to its right-hand side
the term
kgk
2
+ R|g|
−1,2
.
VII.3 The Oseen Fundamental Solution and the
Associated Volume Potentials
In order to derive further properties of solutions to the Oseen problem in
exterior domains, we shall introduce a suitabl e singular solution to equations
(VII.0.3)
1,2
in the whole space. Though such a solution can be considered, for
the probl em at hand, the analogue of the Stokes fundamental solution (IV.2.3),
(IV.2.4), it differs from this latter in several respects; the main difference is the
behavior at large distances. Specifically, the Oseen fundamental solution has
a “no nsym metric” structure, presenting a “wake region” which, as we know,
does not appear i n the Stokes approximation.
Following Oseen (1927, §4), we denote by E and e tensor and vector fields,
respectively, defined by
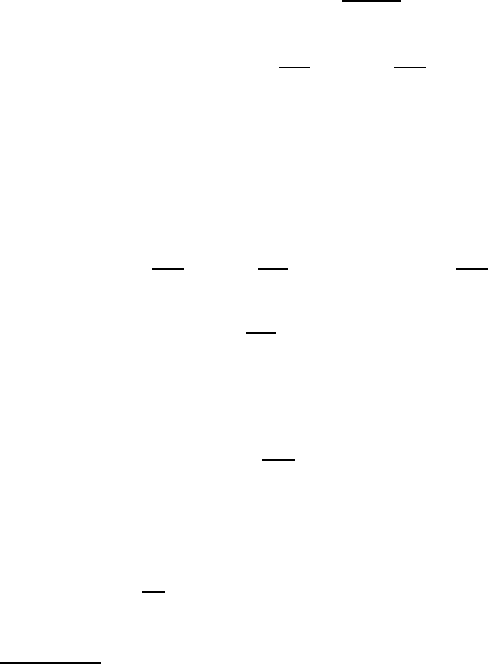
430 VII Steady Oseen Fl ow in Exterior Domains
E
ij
(x, y) =
δ
ij
∆ −
∂
2
∂y
i
∂y
j
Φ(x, y)
e
j
(x, y) = −
∂
∂y
j
∆ − 2λ
∂
∂y
1
Φ(x, y).
(VII.3.1 )
Here i, j = 1, . . . , n, λ = R/2 , while Φ(x, y), with x, y ∈ R
n
, is any real
function that is smooth for x 6= y. Moreover, the Laplace operator acts on the
y-variables. Observe that if λ = 0 , E and e formally coincide with U and q
introduced in (IV.2.1 ). It i s at once checked that fields (VII.3.1) satisfy the
following relations for all x 6= y and all i, j = 1, . . ., n
∆ − 2λ
∂
∂y
1
E
ij
−
∂
∂y
i
e
j
= δ
ij
∆
∆ − 2λ
∂
∂y
1
Φ
∂
∂y
`
E
`j
= 0.
(VII.3.2 )
In order to render (VII.3.1) a singular solution to (VII.0.3)
1,2
, as in the case
of the Stokes system, we choose the function Φ such that
∆
∆ − 2λ
∂
∂x
1
Φ(x, y) = ∆E(|x −y|), (VII.3.3)
where, we recall, E(x) is the fundamental solutio n (II.9.1) to the Laplace
equation.
1
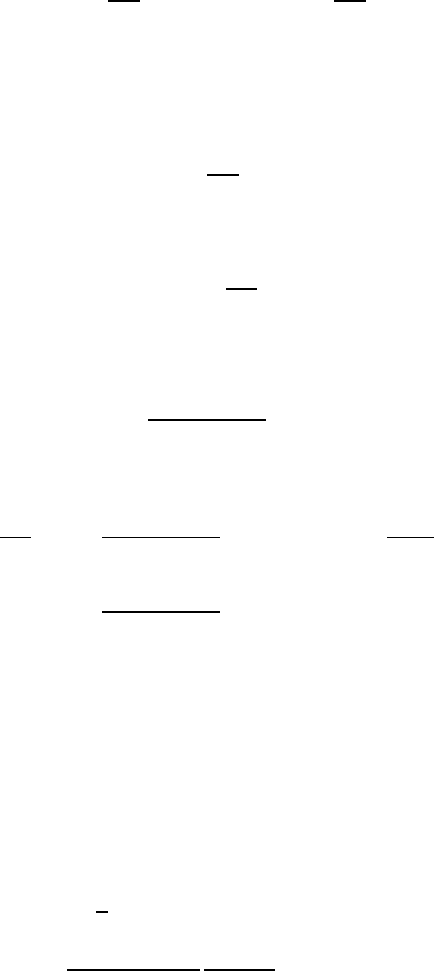
A solution to (VII.3.3) is now sought into the form
Φ(x, y) =
1
2λ
Z
x
1
−y
1
[Φ
2
(τ, x
2
− y
2
, . . . , x
n
− y
n
)
−Φ
1
(τ, x
2
− y
2
, . . ., x
n
− y
n
)]dτ
(VII.3.4 )
1
Let L be a (spatial) differential operator and let h(x, y) be a smooth function of
x, y ∈ R
n
except at x = y. By the notation
Lh(x, y) = ∆E(|x − y|) (∗)
we mean, as customary, Lh(x, y) = 0 for all x 6= y, while, at x = y, h(x, y)
becomes singular in such a way that for any ψ ∈ C
∞
0
(R
n
) it holds that
Z
R
n
h(x, y)L
∗
ψ(y)dy = ψ(x),
where L
∗
denotes the formal adjoint of L. Another usually adopted way of writ ing
(∗) is
Lh(x, y) = δ(x − y),
where δ(x) is the symbolic Dirac function, i.e., a distribution defined by the formal
relation
Z
R
n
δ(x)ψ(x) = ψ(0)
for all ψ ∈ C
∞
0
(R
n
).
VII.3 The Oseen Fundament al Solution 431
with Φ
1
and Φ
2
to be selected appropriately. Replacing formally (VII.3.4) into
(VII.3.3 ) we obtain that Φ
2
− Φ
1
must obey
∆
∆ − 2λ
∂
∂y
1
(Φ
2
−Φ
1
) = −2λ∆(
∂E
∂y
1
). (VII. 3.5)
Choosing
Φ
2
(x, y) = E(|x −y|), (VII.3.6)
for Φ
1
to be a solution to (VII.3.5) it is sufficient to take
∆ − 2λ
∂
∂y
1
Φ
1
= ∆E. (VII.3.7 )
We notice, in passing, that with the above choice o f Φ, from (VII.3.1)
2
we
may take
e
j
(x, y) = −
∂
∂y
j
E(|x − y|), (VII.3.8 )
which shows that the “pressure” e
j
coincides with the “pressure” q
j
of the
fundamental Stokes solution, see (IV.2.3)
2
, (IV.2.4)
2
. Writing
Φ
1
=
e
−λ(x
1
−y
1
)
|x − y|
(n−2)/2
f(λ|x − y|), (VII.3.9 )
by a direct computation we deduce
∆ − 2λ
∂
∂y
1
Φ
1
=
e
−λ(x
1
−y
1
)
|x − y|
(n+2)/2
(
z
2
f
00
+ zf
0
−
"
n − 2
2
2
+ z
2
#
f
)
≡
e
−λ(x
1
−y
1
)
|x − y|
(n+2)/2
L(f),
where z = λ|x − y| and the prime denotes differentiatio n with respect to
z. Now the equation L(f) = 0 is the well-known Bessel’s modified equation
which admits two independent soluti ons,
I
(n−2)/2
(z) and K
(n−2)/2
(z),
called modified Bessel functions of the first and of the second kind, respectively
(MacRobert 1966, §100). However, I
(n−2)/2
(z) is regular for all values of the
argument, while K
(n−2)/2
(z) is singula r at z = 0 in such a way that
K
(n−2)/2
(z) = log
1
z
+ log 2 − γ + σ
1
(z), if n = 2
K
(n−2)/2
(z) =
2
(n−2)/2
Γ (n/2)
n − 2
1
z
(n−2)/2
+ σ
2
(z), if n > 2,
(VII.3.1 0)
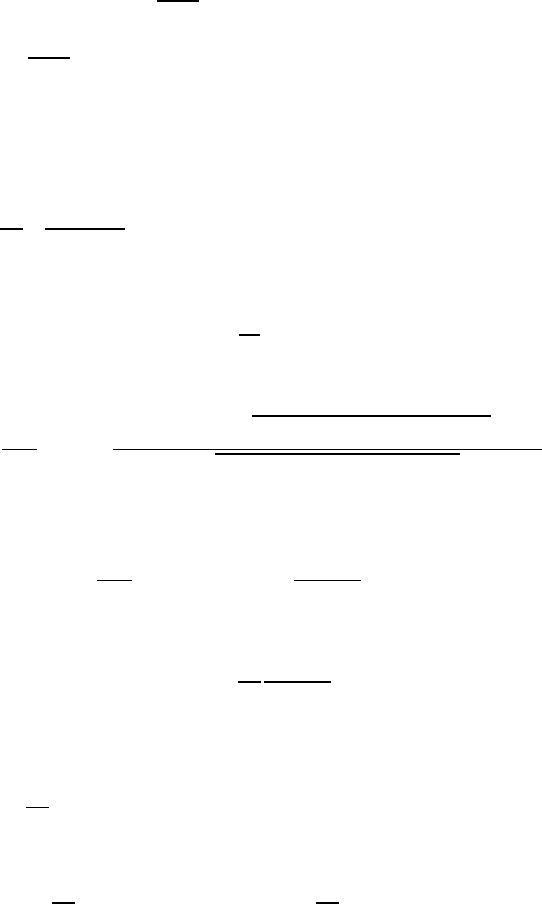
432 VII Steady Oseen Fl ow in Exterior Domains
where γ is the Euler constant, Γ is the gamma function, and the remainders
σ
i
satisfy
σ
1
(z) = o(1),
d
k
σ
1
dz
k
= o(z
−k
), k ≥ 1 as z → 0
d
k
σ
2
dz
k
=o(z
(2−n)/2−k
), k ≥ 0 as z → 0
(Watson 1962, p. 80). Since Φ
1
must satisfy (VII. 3.7) in the neighborhood
of z = 0, it has to behave there like the fundamental solution E. Thus, with
a view to (II.9.1) and taking into account that ω
n
= 2π
n/2
/nΓ (n/2), from
(VII.3.9 ) and (VII.3.10) it follows that we must take
Φ
1
= −
1
2π
λ
2π|x − y|
(n−2)/2
K
(n−2)/2
(λ|x − y|)e
λ(y
1
−x
1
)
. (VII.3.11)
For n = 3, K
1/2
(z) takes the following simple form (Watson 1962, p. 80):
K
1/2
(z) =
π
2z
1/2
e
−z
, (VII.3.12)
and consequently, from (VII.3.4), (VII. 3.6), and (VII.3.11) we obtain
Φ(x −y) =
1
8πλ
Z
x
1
−y
1
1 − exp
n
−λ
h
p
τ
2
+ (x
2
− y
2
)
2
+ (x
3
−y
3
)
2
−τ
io
p
τ
2
+ (x
2
− y
2
)
2
+ (x
3
−y
3
)
2
dτ.
Therefore, fixing the constant up to which Φ is defined by requiring Φ(0) = 0,
it follows that
Φ(x − y) =
1
8πλ
Z
λ(|x−y|+(x
1
−y
1
))
0
1 − e
−τ
τ
dτ. (VII.3.13)
Correspondingly, the pressure field e given in (VII.3.8) takes the form
e
j
(x − y) =
1
4π
x
j
− y
j
|x −y|
3
. (VII.3.14)
Let us now consider the case n = 2. From (VII.3.4), (VII.3.6) and (VII .3.11)
we find
Φ(x − y) =
1
2λ
Z
x
1
−y
1
0
[Φ
2
(τ, x
2
− y
2
) −Φ
1
(τ, x
2
− y
2
)] dτ + Φ
0
(x
2
−y
2
)
where
Φ
2
(x − y) =
1
2π
log |x − y|, Φ
1
(x − y) = −
1
2π
K
0
(λ|x − y|)e
λ(y
1
−x
1
)
and Φ
0
is a function of x
2
− y
2
only, to be fixed appropriately. The function
K
0
(z) cannot be expressed in terms of elementary functions; however, we can
provide an asymptotic expansion f or large z:
VII.3 The Oseen Fundament al Solution 433
K
0
(z) =
π
2z
1/2
e
−z
"
ν−1
X
k=0
Γ (k + 1/2)
k!Γ (1/2 − k)
(2z)
−k
+ σ
ν
(z)
#
=
π
2z
1/2
e
−z
1 −
1
8z
+
9
2!(8z)
2
+ . . . + σ
ν
(z)
,
(VII.3.1 5)
where
d
k
σ
ν
dz
k
= O(z
−k−ν
) as z → ∞, k ≥ 0
(Watson 1962, p. 202). In order to choose Φ
0
, we observe that from (VII.3.6),
(VII.3.7 ) it follows that
∂
2
∂y
2
2
(Φ
2
−Φ
1
) = −
∂
∂y
1
∂
∂y
1
(Φ
2
− Φ
1
) + 2λΦ
1
,
and so
∂
2
Φ
∂y
2
2
= −
1
2λ
∂
∂y
1
(Φ
2
− Φ
1
) + 2λΦ
1
+
1
2λ
∂
∂y
1
(Φ
2
− Φ
1
) + 2λΦ
1
y
1
=x
1
+
∂
2
Φ
0
∂y
2
2
.
Since
∂
∂y
1
log |x −y|
y
1
=x
1
=
∂
∂y
1
K
0
(λ|x − y|)
y
1
=x
1
= 0,
we conclude
∂
2
Φ
∂y
2
2
= −
1
2λ
∂
∂y
1
(Φ
2
−Φ
1
) + 2λΦ
1
+
1
4π
K
0
(λ|x
2
− y
2
|) +
∂
2
Φ
0
∂y
2
2
.
Now, l etting x
2
−y
2
→ 0 in this relation, K
0
(λ|x
2
−y
2
|) diverges logarithmi-
cally fast, while the first three terms on the right-hand side remain bounded.
This would lead, by (VII.3.1), to an unacceptable singularity for E
22
, unless
we choose Φ
0
in such a way that
Φ
00
0
(t) = −
1
4π
K
0
(λ|t|).
If we do this and impose Φ
0
(0) = Φ
0
(0) = 0, we find
Φ
0
(x
2
− y
2
) = −
1
4π
Z
y
2
−x
2
0
(y
2
− x
2
− τ)K
0
(λ|τ|)dτ,
which, in turn, furnishes the following expression for Φ:

434 VII Steady Oseen Fl ow in Exterior Domains
Φ(x − y) =
1
4πλ
Z
x
1
−y
1
0
n
log
p
τ
2
+ (x
2
− y
2
)
2
+K
0
λ
p
τ
2
+ (x
2
−y
2
)
2
e
−λτ
dτ
−
1
4π
Z
y
2
−x
2
0
(y
2
−x
2
− τ)K
0
(λ|τ|)dτ.
(VII.3.1 6)
Correspondingly, the pressure field e (VII.3.8) becomes
e
j
(x − y) =
1
2π
x
j
− y
j
|x −y|
2
. (VII.3.17)
The pair E, e defined by (VII.3.1), (VII.3.13), and (VII.3.14) for n = 3 and by
(VII.3.1 ), (VII.3.16), and (VII.3 .17) for n = 2 is called the Oseen fundamental
solution. In arbitrary dimensions n > 3, the Oseen fundamental solutio n is
defined by (VII.3.1), (VII.3.4), (VII.3.8), and (VII.3.11). In view of (VII.3.2)
and (VII.3.3) this solution satisfies
∆ − 2λ
∂
∂y
1
E
ij
(x − y) =
∂
∂y
i
e
j
(x − y)
∂
∂y
`
E
`j
(x − y) = 0
for x 6= y; (VII.3.18)
this is the system adjoint to (VII.0.3). However, since
∂E
ij
∂x
1
= −
∂E
ij
∂y
1
∂e
j
∂x
1
= −
∂e
j
∂y
1
we also have
∆ + 2λ
∂
∂x
1
E
ij
(x − y) =
∂
∂x
i
e
j
(x − y)
∂
∂x
`
E
`j
(x − y) = 0
for x 6= y (VII.3.19)
with ∆ op erating now on the x-variables.
We wish to investigate the properties of E(x) and e(x) for large |x|. While
those of e are quite obvious, those of E require a little more care. Let us
begin to consider the case where n = 3. Setting r = |x −y|, s = λ(r + x
1
−y
1
)
from (VII.3.1)
1
and (VII.3.13) we derive the following expression for the nine
components o f the tensor E

VII.3 The Oseen Fundament al Solution 435
E
11
(x − y) =
1
4πr
−e
−s
+
1
2λr
x
1
−y
1
r
(1 − e
−s
) + se
−s
E
22
(x − y) = −
e
−s
4πr
+
1
8π
1
r
−
(x
2
− y
2
)
2
r
3
1 − e
−s
s
+ λ
se
−s
−1 + e
−s
s
2
(x
2
− y
2
)
2
r
2
E
33
(x − y) = −
e
−s
4πr
+
1
8π
1
r
−
(x
3
− y
3
)
2
r
3
1 − e
−s
s
+ λ
se
−s
−1 + e
−s
s
2
(x
3
− y
3
)
2
r
2
E
12
(x − y) = E
21
(x − y) =
1
8πr
y
2
− x
2
r
e
−s
−
1 − e
−s
λr
E
13
(x − y) = E
31
(x − y) =
1
8πr
y
3
− x
3
r
e
−s
−
1 − e
−s
λr
E
23
(x − y) = E
32
(x − y) =
1
8π
(x
2
−y
2
)(x
3
− y
3
)
r
3
e
−s
−1
s
+ λr
se
−s
−1 + e
−s
s
2
.
(VII.3.2 0)
From (VII.3.20) it readily follows that in the limit of vanishing λr the tensor
E reduces to the tensor U (IV.2. 3)
1
associated to the Stokes fundamental
solution. Specifically, we have
E
ij
(x − y) = U
ij
(x − y) + o(1), as λr → 0. (VII.3.21)
In view of (VII.3.21) and (VII.3.1 4), from the calculations leading to (IV.8.15)
we can then show that the Oseen fundamental solution E, e becomes si ngular
at x = y in such a way that, for any vector field v continuous at x and all
j = 1, 2, 3, it holds that
lim
ε→0
Z
|x−y|=ε
v · T (w
j
, e
j
) · ndσ
y
= −v
j
(x), (VII.3.22)
where n is the outer normal to ∂B
ε
(x) and
w
j
≡ (E
1j
, E
2j
, E
3j
).
The estima tes of E(x−y) at infinity are, however, completely different from
those of U (x −y). Denote by ϕ the polar angle made by a ray that starts from
x and is directed toward y with the positively directed x
1
-axis. We present the
