Габбасова Ж.Д. Автоматизированные технологические процессы

Подождите немного. Документ загружается.

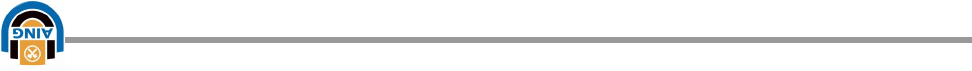
Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

Назначение и состав системы VisSim 4.5. Система VisSim (для

определенности наиболее распространенная версия VisSim 4.5)

предназначена для решения задач математического моделирования,

относящихся к следующим классам:

 линейные системы;

 нелинейные системы;

 непрерывные во времени системы;

 дискретные во времени системы;

 системы с изменяемыми во времени параметрами;

 гибридные системы;

 многоцелевые и многокомпонентные системы;

 одновходовые и одновыходные (одномерные) системы SISO;

 многовходовые и многовыходовые (многомерные) системы

MIMO;

 гибридные системы.

Система VisSim не имеет явной ориентации на какой-то класс

моделирования. Это универсальная система, допускающая достаточно

простое расширение и обеспечивающая легкую адаптацию под решение тех

или иных конкретных задач пользователя. Тем не менее, считать, что

наиболее удобна данная система для решения задач в области

автоматического регулирования и управления, а также при моделировании

различных физических, химических, экономических и прочих явлений и

систем.

VisSim 4.5 может работать в среде операционных систем Windows 95/98

NT 4+. Была проведена работоспособность системы в среде Windows

2000/ХР. Никаких отклонений в работе системы выявлено не было. VisSim

требует весьма скромных аппаратных ресурсов – ПК должен иметь

оперативную память с минимальным объемом 4 Мб и объемом свободного

пространства на жестком диске около 30 Мб. Обязательно наличие

математического сопроцессора, поскольку в ходе моделирования широко

используется 64-битный формат чисел с плавающей точкой,

обеспечивающий очень малые вычислительные погрешности.

Для построения моделей в системе VisSim используются блоки, которые

хранятся в библиотеке блоков и могут браться из нее, переноситься в окно

модели и соединяться друг с другом.

Библиотека блоков, представленная в позиции Blocks (Блоки) меню и

инструментальными панелями, содержит следующие «тома»:

 Animation – блоки создания анимационных клипов;

 Annotation – блоки создания комментариев и определения

переменных;

 Arithmetic – блоки арифметических и близких к ним операций;

 Boolean – блоки задания операций Булевой алгебры;

 DDE – блоки интерфейса;

 Integration – блоки задания операций интегрирования;

51 (107)

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

 Linear Systems – блоки задания параметров пространства

состояний линейных систем и их передаточных функций;

 MATLAB Interface – блоки интеграции с математичкой системой

MATLAB;

 Matrix Operations – блоки задания матричных операций;

 Nonlinear – блоки нелинейных операций и создания нелинейных

систем;

 Optimization – блоки задания операций оптимизации;

 Random Generator – блоки генерации случайных чисел;

 Real Time – блоки для систем реального времени;

 Signal Consumer – блоки регистрации, индикации и построения

графиков сигналов;

 Signal Producer – блоки создания сигналов;

 Time Delay – блоки создания временной задержки;

 Transcendental – блоки задания трансцендентных математические

функций;

 General – функции общего характера.

Литература: 6 осн. [6-10, 14-17, 23-24, 55-58, 85-89], 10 доп. [67-82]. 9

доп. [43-48].

ЛЕКЦИЯ 7. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

7.1. Основные понятия нахождения экстремума функции

Всякая математическая постановка оптимальной задачи часто

равносильна или эквивалентна задаче отыскания экстремума функции одной

или многих независимых переменных. Поэтому для решения таких

оптимальных задач могут быть использованы различные методы поиска

экстремума.

В общем случае задача оптимизации формулируется следующим

образом:

Найти extr функции R(x), где Х



R(x) – называется целевой функцией или функцией или критерием

оптимизации или оптимизируемой функцией

Х – независимая переменная.

Как известно необходимые условиям существования экстремума у

непрерывной функции R(x) могут быть получены из анализа первой

производной

. При этом функция R(x) может иметь экстремальные

значения при таких значениях независимой переменной Х, где первая

производная

равна 0. т.е.

=0. Графически равенство нулю

52 (107)

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

производной означает, что касательная к кривой R(x) в этой точке

параллельна оси абсцисс. (Рис. 6.1)

Рис. 6.1

Равенство производной

=0 есть необходимое условие экстремума.

Однако равенство нулю производной еще не означает, что в этой точке

существует экстремум. Для того, чтобы окончательно убедится, что в этой

точке действительно существует экстремум необходимо провести

дополнительные исследования, которые заключаются в следующих способах:

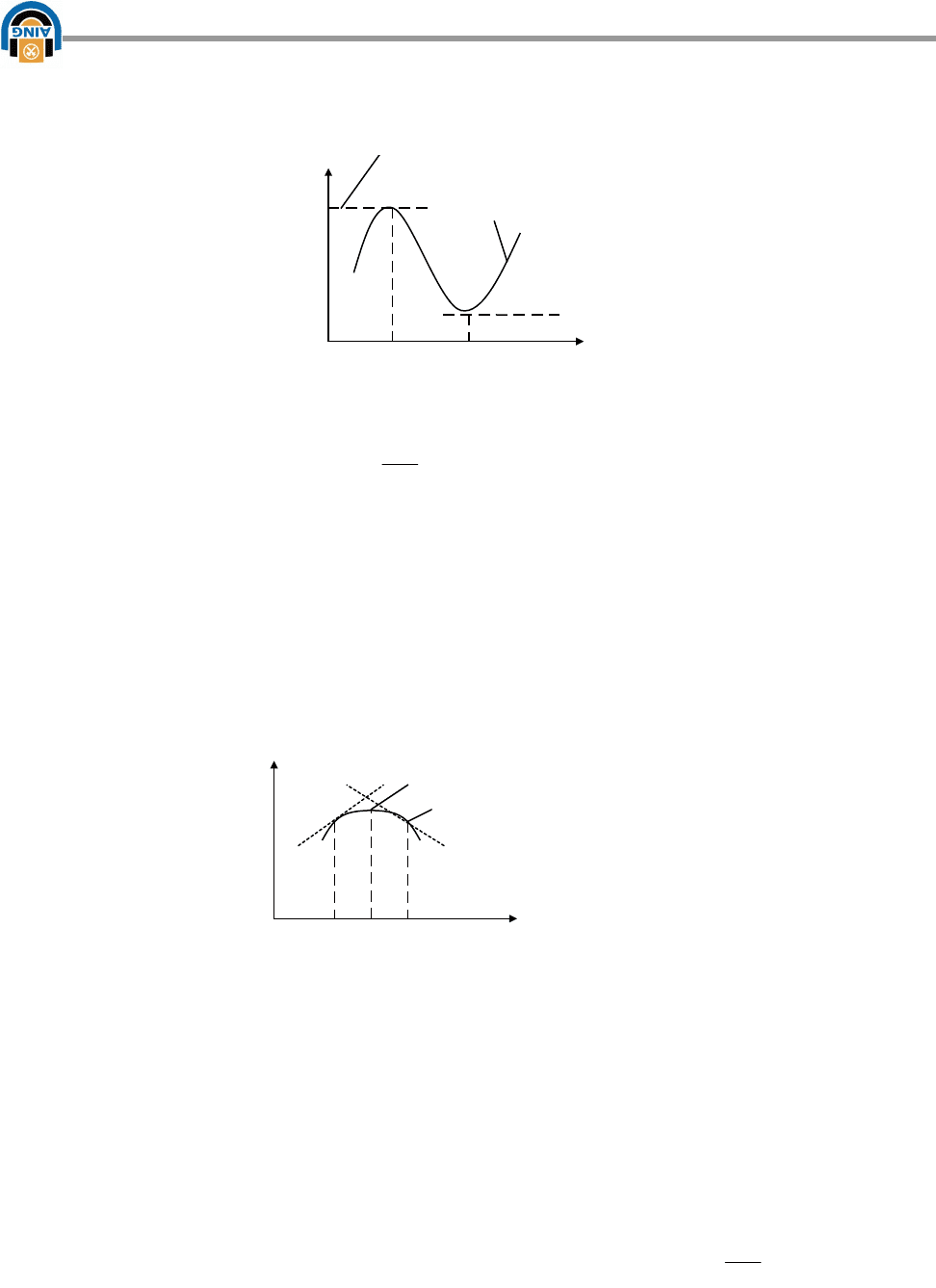
1. Способ сравнения значений функций

Сравнивают значение функции R(x) в «подозреваемой» на экстремум

точке Х

две соседние значения функции R(x) в точках Х

К-ε

и Х

К+ε

, где ε-

малая положительная величина. (Рис. 6.2)

Рис. 6.2

Если оба рассчитанных значения R(Х

К+ε

) и R(Х

К-ε

), окажутся меньше

или больше R(Х

), то в точке Х

существует максимум или минимум

функции R(х).

Если же R(Х

) имеет промежуточное значение между R(Х

К-ε

) и R(Х

К+ε

то функция R(х) не имеет ни максимума ни минимума.

2.Способ сравнения знаков производных

Опять рассмотрим функцию R(Х

) в окрестностях точки Х

, т.е. Х

К+ε

К-ε

. При этом способе рассматривается знак производной

в окрестности

точки Х

. Если знаки производной в точках Х

К-ε

и Х

К+ε

различные, то в точке

существует экстремум. При этом вид экстремума (min или max) может

быть найден по изменению знака производной при переходе от точки Х

К-ε

точке Х

К+ε.

53 (107)

R(x)

К+ε

R(x-ε)

R(x)

К-

R(x+

ε)

R(x)

касательная

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

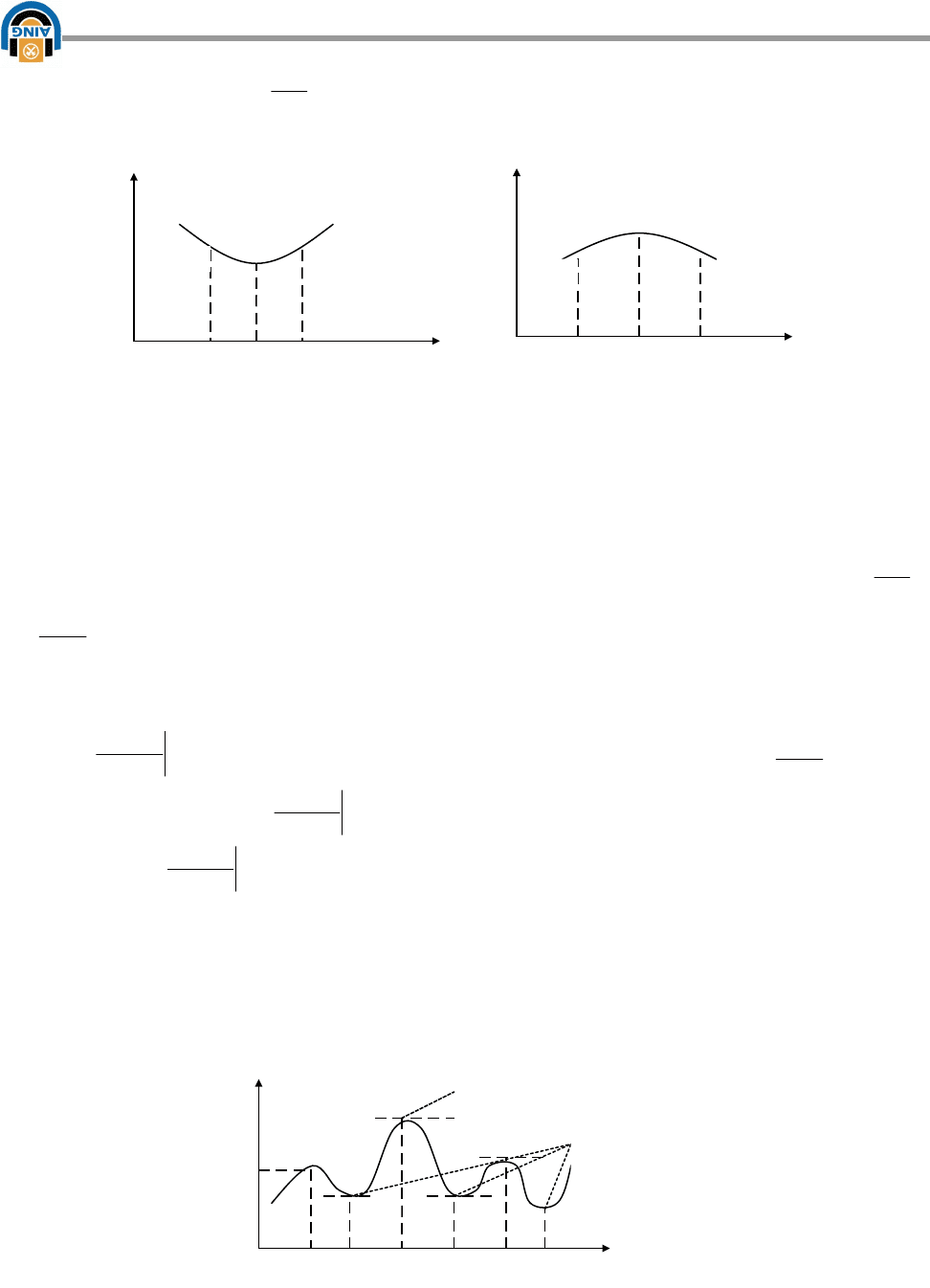
Если знак

меняется с «+» на «-», то в точке Х

– максимум

(рис.6.3б), если наоборот с «-» на «+», то минимум. (Рис. 6.3а)

Рис.6.3

3.Способ исследования знаков высших производных.

Этот способ применяют в тех случаях, когда в точке «подозреваемой»

на экстремум существуют производные высших порядков, т.е. функция R(Х

)

не только сама непрерывна, но имеет также непрерывные производные

Способ сводится к следующему:

В точке Х

«подозреваемой» на экстремум, для которой справедливо

)(



XdR

вычисляется значение второй производной

Если при этом

)(





XdR

, то в точке Х

– максимум,

если

)(





XdR

, то в точке Х

– минимум.

При решении практических задач оптимизации требуется отыскать не

какое-нибудь min или max значение функции R(Х

), а наибольшее или

наименьшее значение этой функции, которое называется глобальным

экстремумом. (Рис.6.4)

Рис.6.4

54 (107)

К+ε

R(x)

К-1

К+ε

R(x)

К-1

а) б)

R(x)

глобальный

экстремум

локальный

экстремум

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

В общем случае задача оптимизации состоит в отыскивании

экстремума функции R(Х), при наличии тех или иных ограничений на

уравнения математической модели.

В том случае, если R(Х) является линейной, а область допустимых

решений задается линейными равенствами и неравенствами, то задача

отыскания экстремумов функции относится к классу задач линейного

программирования.

Часто множество Х определяют как систему функции











0)(

Тогда запись математической постановки задачи линейного

программирования выглядит так:



,0)()( XCXRexstr

0)( XH

В том случае, если или целевая функция R(Х) или какая-либо из

ограничений не является линейной функцией, то задача отыскания

экстремума функции R(Х) относится к классу задач нелинейного

программирования.

В том случае, если на переменные Х не наложено никаких ограничений,

то такая задача называется задачей на безусловный экстремум.

Пример типовой задачи оптимизации

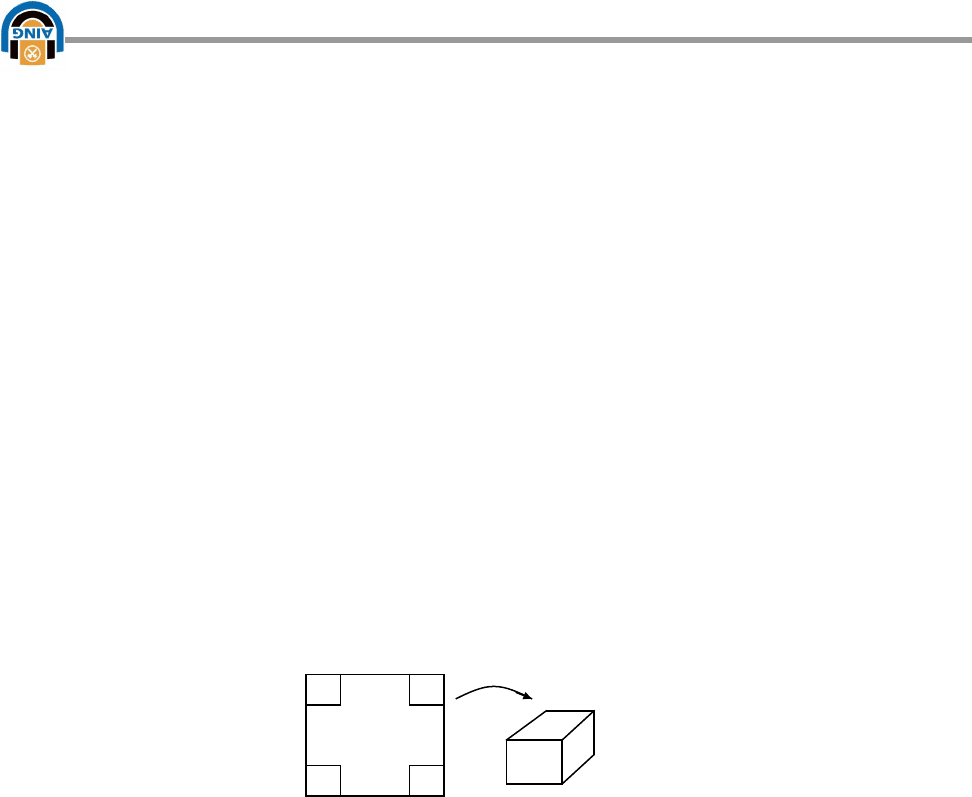
Задача о коробке максимального объема.

Содержательная постановка задачи формируется следующим образом.

Имеется квадратная заготовка из некоторого гибкого материала (картон,

жесть). Размеры этой заготовки фиксированы конкретной ситуации. (Рис.6.5)

Из этой заготовки следует вырезать четыре ровных квадрата по ее

углам, а полученную фигуру (рис.6.5 б) согнуть так, чтобы получилась

коробка без верхней крышки (рис.6.5 в). при этом необходимо так выбрать

размер вырезаемых квадратов, чтобы получилась коробка максимального

объема.

На примере данной задачи можно проиллюстрировать все элементы

постановки задач оптимизации.

а) б) в)

Рис. 6.5. Схема изготовления коробки из прямоугольной заготовки

фиксированного размера

Оценочной функцией в данной задаче служит объем изготовленной

коробки. Проблема заключается в выборе размера вырезаемых квадратов.

Действительно, если размер вырезаемых квадратов слишком мал, то будет

получена широкая коробка малой высоты, а значит и объем окажется

невелик. С другой стороны, если размер вырезаемых квадратов будет

слишком большой, то будет получена узкая коробка большой высоты, а

значит, и ее объем также окажется невелик.

55 (107)

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

В то же время на выбор размера вырезаемых квадратов оказывает

влияние ограничение размера исходной заготовки. Действительно, если

вырезать квадраты со стороной, равной половине стороны исходной

заготовки, то задача теряет смысл. Сторона вырезаемых квадратов также не

может превышать половину сторон исходной заготовки, поскольку это

невозможно из практических соображений. Из этого следует, что в

постановке данной задачи должны присутствовать некоторые ограничения.

Математическая постановка задачи о коробке максимального объема.

Для математической постановки данной задачи необходимо ввести в

рассмотрение некоторые параметры, характеризующие геометрические

размеры коробки. С этой целью дополним содержательную постановку

задачи соответствующими параметрами. С этой целью будем рассматривать

квадратную заготовку из некоторого гибкого материала, которая имеет длину

стороны L (рис.6.6). Из этой заготовки следует вырезать четыре ровных

квадрата со стороной по ее углам, а полученную фигуру согнуть, так чтобы

получилась коробка без верхней крышки. Задача состоит в таком выборе

размера вырезаемых квадратов, чтобы в результате получилась коробка

максимального объема.

Рис. 6.6. Схема изготовления из прямоугольной заготовки с указанием ее

размеров

Для математической постановки данной задачи необходимо определить

переменные соответствующей задачи оптимизации, задать целевую функцию

и специфицировать ограничения. В качестве переменной следует взять длину

стороны вырезаемого квадрата r, которая в общем случае, исходя из

содержательной постановки задачи, принимает непрерывные действительные

значения. Целевой функцией является объем полученной коробки. Поскольку

длина стороны основания коробки равна: L - 2r, а высота коробки равна r, то

ее объем находится по формуле: V(r) = (L-2r)

r . исходя из физических

соображений, значения переменной r не могут быть отрицательными и

превышать величину половины размера исходной заготовки L, т.е. 0,5L.

Примечание

При значениях r = 0 и r = 0,5 L соответствующие решения задачи о

коробке являются выраженными. Действительно, в первом случае заготовка

остается без изменения, а во втором случае она разрезается на 4 одинаковых

части. Поскольку эти решения имеют физическую интерпретацию, задачу о

коробке для удобства ее постановки и анализа можно считать оптимизации с

ограничениями типа нестрогих неравенств.

56 (107)

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

С целью унификации, обозначим переменную через х = r, что не

оказывает влияния на характер решаемой задачи оптимизации. Тогда

математическая постановка задачи о коробке максимального объема может

быть записана в следующем виде:

   

,max2







xLxxf

где

 

LxRx  5.00



(6.1)

Целевая функция данной задачи является нелинейной, поэтому задача о

коробке максимального размера относится к классу задач нелинейного

программирования или нелинейной оптимизации.

7.3 Классификация методов оптимального управления

Оптимизация процесса заключается в нахождении оптимума

рассматриваемой функции или оптимальных условий проведения данного

процесса.

Для оценки оптимума, прежде всего, необходимо выбрать критерий

оптимизации. Обычно, критерий оптимизации выбирает из конкретных

условий. Это могут быть технологический критерий (например, содержание

Сu в отвальном шлаке) или экономический критерий (минимальная

стоимость продукта при заданной производительности труда) и др. На

основании выбранного критерия оптимизации составляется целевая функция,

представляющая собой зависимость критерия оптимизации от параметров

влияющих на его значение. Задача оптимизации сводится к нахождению

экстремума целевой функции. В зависимости от характера рассматриваемых

математических моделей принимаются различные математические методы

оптимизации.

Общая постановка задачи оптимизации заключается в следующем:

1. Выбирается критерий

2. Составляется уравнение модели

3. Накладывается система ограничения

4. Решение

 

maxJ

модель

 

,tXfY



- линейная или нелинейная

Ограничения



В зависимости от структуры модели применяются различные методы

оптимизации. К ним относятся:

1. Аналитические методы оптимизации (аналитический поиск

экстремума, метод множителей Лагранжа, Вариационные методы)

2. Математическое программирование (линейное программирование,

динамическое программирование)

3. Градиентные методы.

4. Статистические методы (Регрессионный анализ)

Линейное программирование. В задачах линейного программирования

критерий оптимальности представляется в виде:





XCR

где

 

njC

...1

- заданные постоянные коэффициенты

57 (107)

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

- переменные задачи

Уравнения модели представляют собой линейные уравнения

(полиномы) вида







jijj

xaaY

на которые накладывается ограничения в

виде равенства или неравенства, т.е.











iiij

ijij

bxa

bxaили

bxa

(6.2)

В задачах линейного программирования обычно предполагается, что все

независимые переменные Х

неотрицательны, т.е.

0

Оптимальным решением задачи линейного программирования является

такая совокупность неотрицательных значений независимых переменных

îïòèì

XX 

nj ,...1

, которая удовлетворяет условия (6.2) и

обеспечивает в зависимости от постановки задачи max или min значение

критерия.

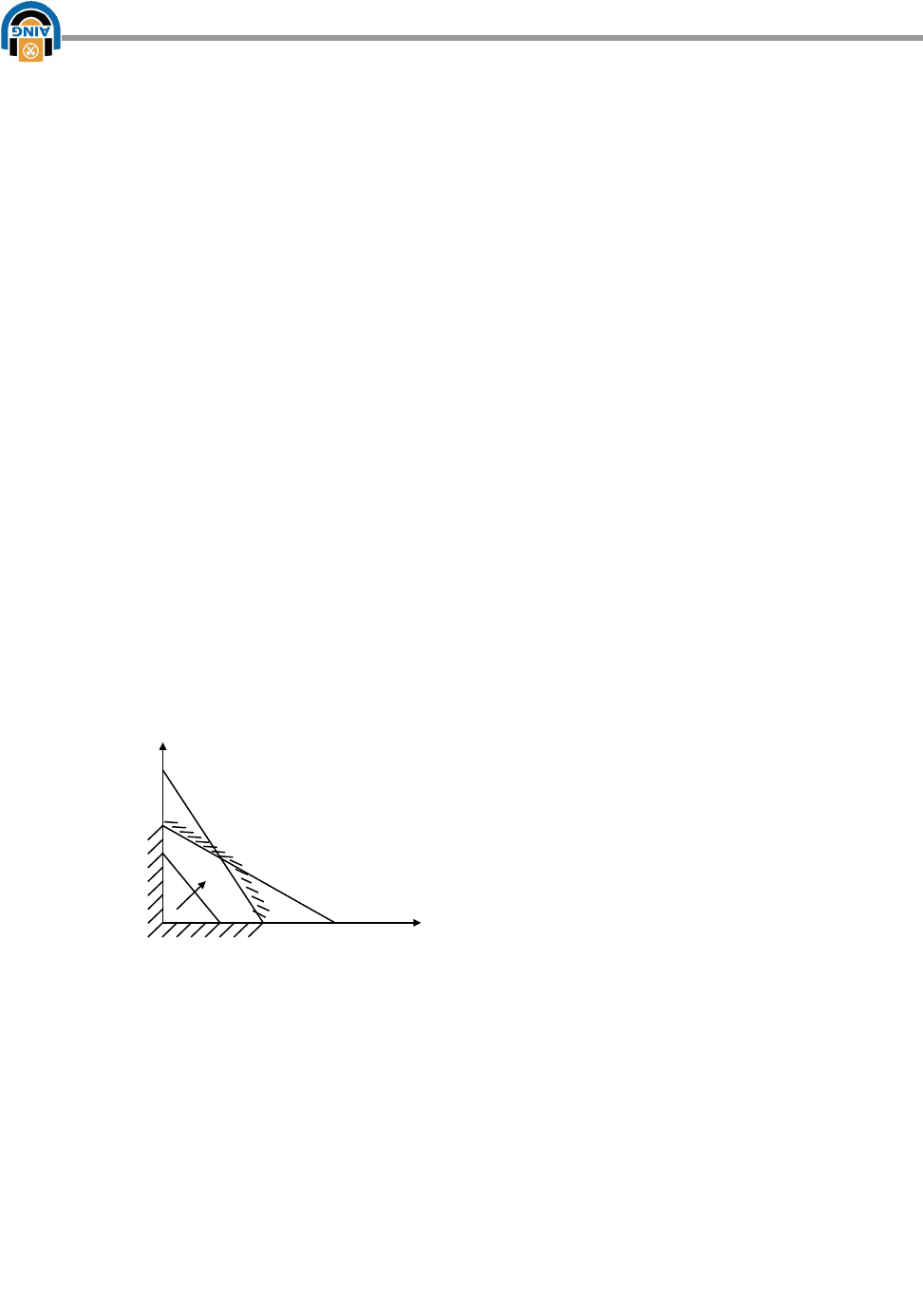
Геометрическая интерпретация (рис.6.7) имеет вид:

max

 XXR

критерий при наличии ограничении на переменных Х

и Х

типа равенств и

неравенств



X

Рис. 6.7

R имеет постоянное значение вдоль линии l. Оптимальное решение

будет в точке S, т.к. в этой точке критерий будет max.Одним из методов

решения задачи оптимизации линейного программирования является

симплекс-метод.

Нелинейное программирование. Математическая постановка задачи

нелинейного программирования заключается в следующем: Найти экстремум

целевой функции

 

xXXRR ,...,



, которая имеет вид нелинейности.

На независимые переменные налагаются различные ограничения типа

равенств или неравенств

 

0,...

0...

321





XXX

XXXX



,...1



в настоящее время для решения задач нелинейного программирования

применяются довольно большое число методов.

58 (107)

•

0 Х

+2X

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

К ним относится: 1) Градиентные методы (метод градиента, метод

наискорейшего спуска, метод образов, метод Розенброка и т.д.)

2) Безградиентные методы (метод Гауса-Зейделя, метод сканирования).

Градиентные методы оптимизации. Эти методы относятся к

численным методам поискового типа. Сущность этих методов

заключается в определении значений независимых переменных, дающих

наибольшее (наименьшее) изменение целевых функции. Обычно это

достигается при движении вдоль градиента, ортогонального к

контурной поверхности в данной точке.

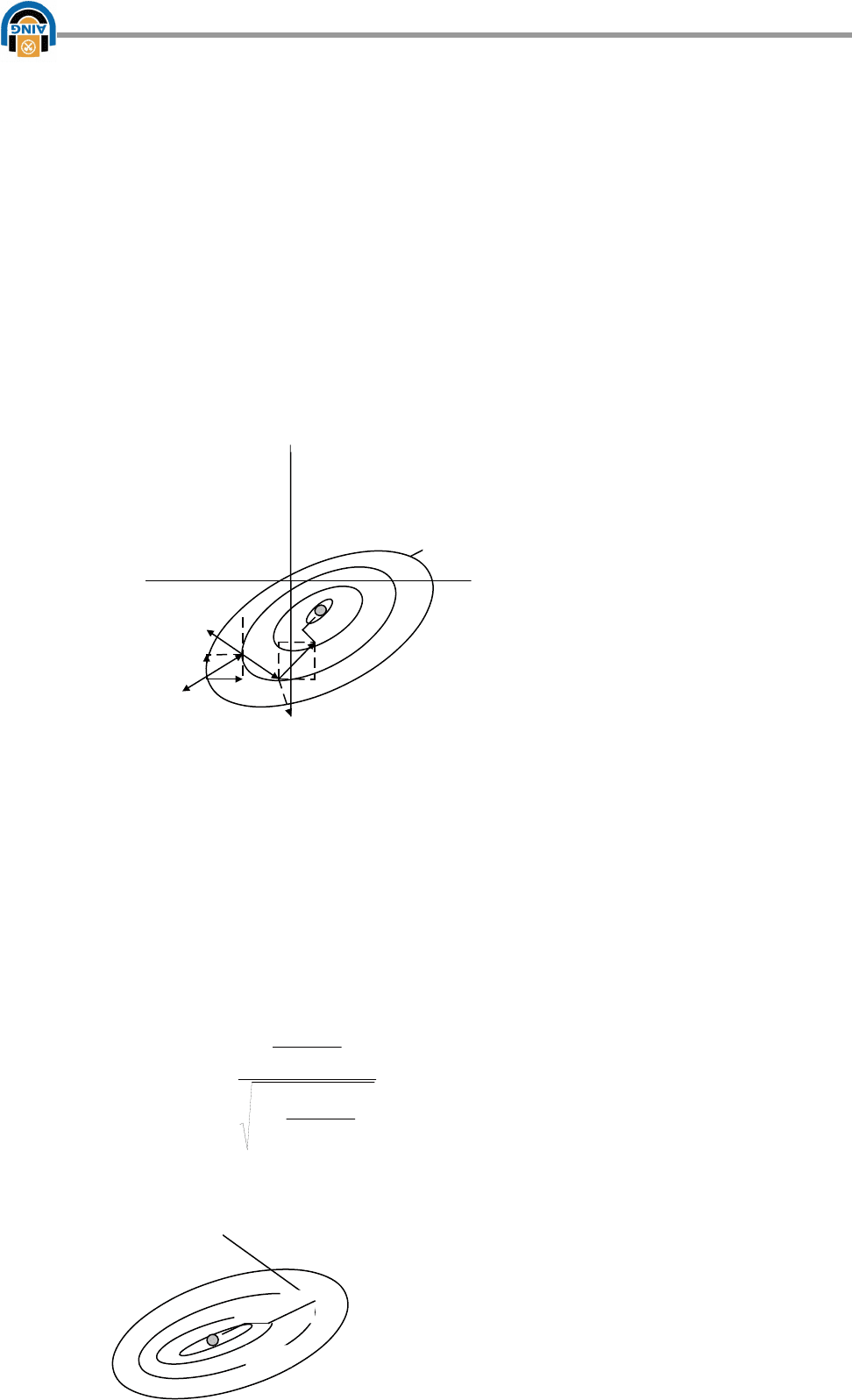
Рассмотрим метод градиента. В этом методе используется градиент

целевой функции. В методе градиента шаги совершаются в направлении

наибыстрейшего уменьшения целевой функции. (Рис. 6.8)

Рис. 6.8 Поиск минимума методом градиента

Поиск оптимума производится в два этапа:

1-этап: - находят значения частных производных по всем независимым

переменным, которые определяют направление градиента в рассматриваемой

точке.

2-этап: - осуществляется шаг в направлении обратном направлению

градиента, т.е. в направлении наибыстрейшего убывания целевой функции.

Алгоритм градиентного метода может быть записан следующим

образом:

     

 























hXX

(6.3)

Характер движения к оптимуму методом наискорейшего спуска

заключается в следующем (рис. 6.9), после того как в начальной точке найден

градиент оптимизируемой функции и тем самым определено направление ее

наибыстрейшего убывания в указанной точке, в данном направлении

делается шаг спуска. Если значение функции в результате этого шага

уменьшилась, то производится очередной шаг в том же направлении, и так до

59 (107)

δx

’

ΔХ

grad

gra

опт

им.

grad

δx

Линия постоянного уровня или

поверхность, если n=3 и >, и

в котором критерий R(Х

)

имеет постоянное значение С

(

•

(В

)

(А

)

(0)

Атырауский институт нефти и газа

УМК. Автоматизация технологических процессов. Издание первое.

тех пор, пока в этом направлении не будет найден минимум, после чего

вычисляется снова градиент и определяется новое направление

наибыстрейшего убывания целевой функции.

Рис. 6.9

Безградиентные методы поиска экстремума. Эти методы, в отличии от

градиентных, используют в процессе поиска информации, получаемую не

при анализе производных, а от сравнительной оценки величины критерия

оптимальности в результате выполнения очередного шага.

К безградиентным методам поиска экстремума относится:

1. метод золотого сечения

2. метод с использованием чисел Фибония

3. метод Гауса-Зейделя (метод получения изменения переменной)

4. метод сканирования и т.д.

Литература: 10 доп. [202-204, 205-210, 225-230]; 11 доп. [14-15, 107-

109]

ЛЕКЦИЯ 8. АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ

УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

8.1 Структура современной АСУТП, ее функции и основные

разновидности

Назначение, цели и функции АСУТП. Назначение современных АСУТП

можно определить, как целенаправленное ведение технологического

процесса и обеспечение смежных и вышестоящих систем управления

необходимой информацией.

Во многих ситуациях назначением АСУТП является достижение

реализуемости и устойчивости технологического процесса при высоких

интенсивных и экономичных режимах использования оборудования.

Создание и функционирование каждой АСУТП должно быть

направлено на получение определенных технико-экономических результатов

(снижение себестоимости продукции, уменьшение потерь, повышение

производительности труда, качества продуктов, улучшение условий труда

персонала и т.д.)

60 (107)

(

•

(В

)

(А

)

(0)