Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing

Подождите немного. Документ загружается.

230 5 Quantum Error Correction

The quality of the error correction can be assessed via the ﬁdelity F D

hψ

jO

out

jψ

i,wherejψ

i represents the input state and O

out

corresponds to

the output state of the error correction circuit [203, 211, 212]. Here, the ﬁdelity is

calculated as

F D



1 C 4

(

∆ Ox

out

)

E

1 C 4

(

∆ Op

out

)

E

, (5.12)

where Ox

out

and Op

out

are quadrature operators of the output ﬁeld. For example, in

the case of an error in channel 1, the output quadrature operators become

out

DOx



(0)

an1

r

out

DOp



(0)

an2

r

, (5.13)

where Ox

, Op

, Ox

(0)

an1

,and Op

(0)

an2

arequadratureoperatorsoftheinputﬁeldandthe

ancilla vacuum modes, and r

are squeezing parameters for ancilla i.Intheideal

case of r

!1, unit ﬁdelity is obtained with output states approaching the input

states. For zero squeezing, Eq. (5.13) yields an excess noise of 1/2 and 1/6 for the x

and p quadratures corresponding to 1.76 and 0.67 dB of output powers, respectively

(see Table 5.2 and all the experimental results are summarized in the table).

Equation (5.12) can be used to translate the measured noise level values from

Table 5.2 into ﬁdelity values. Indeed, for every possible error introduced (in any

of the channels), the ﬁdelity after error correction exceeds the maximum values

achievable for the scheme in the absence of ancilla squeezing. For example, for an

error in mode 1, a ﬁdelity of 0.88 ˙ 0.01 was achieved (exceeding the “classical”

cutoff of 0.86). Similarly, for an error in channel 9, we obtain a ﬁdelity o f 0.86 ˙

0.01, exceeding a cutoff of 0.82 (The lower cutoff takes into consideration that only

two of the four nonzero components are used.). The improvement over quantum-

limited ﬁdelities for errors in any one of the nine channels is the key demonstration

of this experiment, providing indirect evidence of entanglement-enhanced error

correction. By comparison, in compl ete absence of any error correction, that is,

without reversing displacement errors (including the zero-squeezing case; for an

application of such quantum-limited error correction), ﬁdelity values under 0.007˙

0.001 were obtained. Nonetheless, instead of this absolute improvement, it is the

extent to which the classical cutoff is exceeded which quantiﬁes the effectiveness

of the nonclassical resources.

In the experiment of [239], evidence is obtained for an entanglement-enhanced

correction of displacement errors; a further increase of the small enhancement of

that implementation would only require higher squeezing levels of the resource

states. The scheme could be useful for applications where stochastic errors occur

such as free-space communication with ﬂuctuating losses and beam pointing er-

rors [250–253].

5.4 Entanglement Distillation 231

Table 5.2 Output noise power of QEC circuit in dB, relative to the shot noise level. Perfect error

correction therefore corresponds to 0 dB. SQ: squeezing.

Error Quadrature Output power Output power Output power

on of output without SQ without SQ with SQ

mode (theory) (experiment) (experiment)

1 x 1.76 1.84 ˙0.12 1.46 ˙0.13

p 0.67 0.68 ˙ 0.12 0.57 ˙ 0.12

2 x 1.76 1.75 ˙0.12 1.42 ˙0.13

p 0.87 0.97 ˙ 0.12 0.72 ˙ 0.12

3 x 1.76 1.83 ˙0.12 1.41 ˙0.12

p 0.87 0.92 ˙ 0.12 0.70 ˙ 0.12

4 x 2.22 2.26 ˙0.12 1.67 ˙0.12

p 0.67 0.73 ˙ 0.12 0.50 ˙ 0.12

5 x 2.22 2.33 ˙0.12 1.79 ˙0.12

p 0.87 0.88 ˙ 0.12 0.73 ˙ 0.13

6 x 2.22 2.34 ˙0.12 1.77 ˙0.12

p 0.87 0.87 ˙ 0.13 0.73 ˙ 0.13

7 x 2.22 2.30 ˙0.13 1.72 ˙0.12

p 0.67 0.69 ˙ 0.12 0.57 ˙ 0.12

8 x 2.22 2.18 ˙0.13 1.79 ˙0.13

p 0.87 0.84 ˙

0.12 0.65 ˙ 0.12

9 x 2.22 2.18 ˙0.14 1.82 ˙0.13

p 0.87 0.94 ˙ 0.12 0.61 ˙ 0.12

5.4

Entanglement Distillation

Theentanglementofacompositequantumstateisdistillableifasufﬁcientlylarge

number of copies of that state can be converted into a pure maximally entangled

state (or arbitrarily close to it) through local operations and classical communica-

tion. This entanglement distillation is typical ly (but not necessarily) probabilistic.

Although various experiments for distilling pure and even mixed entangled qubit

states have been performed [255–258], the situation for CV entangled states is quite

different. The need for a non-Gaussian element in CV distillation

led to a few

distinct approaches. One such approach is to induce non-Gaussian noise such that

the resulting mixed entangled state is no longer a Gaussian state [250–252, 259,

260], in which case distillation is possible with Gaussian operations. Along these

2) In general, the overall entanglement cannot

be increased deterministically through local

operations and classical communication.

However, this still allows, for instance, to

transform two equally entangled copies into

one more and one less entangled copy in a

deterministic fashion [254].

3) Recall that Gaussian entangled states cannot

be distilled through Gaussian operations

alone (see Chapter 2).

232 5 Quantum Error Correction

lines, channels with random phase ﬂuctuations [252] and random attenuation [251]

have been experimentally demonstrated.

An example of probabilistic entanglement distillation (concentration) of a single

copy of a pure Gaussian two-mode squeezed state (TMSS) into a higher entangled

non-Gaussian (but still inﬁnite-dimensional) state through non-Gaussian opera-

tions, namely, by subtracting photons, was presented in [261]. The original version

of this protocol required photon number resolving (PNR) detectors. Nonetheless,

simple on/off detectors work as well [262]. The entanglement before and after the

distillation can be generally quantiﬁed in a numerical fashion [263] as well as ana-

lytically to some extent [158].

More important and more realistic, however, is the distillation of mixed Gaus-

sian TMSSs because a TMSS will be subject to losses and noise in a channel when

used for communication, and in most experiments, the TMSS is not entirely pure

when the antisqueezing exceeds the squeezing level (see below). An extended theo-

retical analysis of photon-subtraction-based distillation techniques including Gaus-

sian mixed states as resources can be found in [158]. This type of distillation was

recently demonstrated experimentally [264].

In order to understand single-copy distillation through photon subtraction, con-

sider a TMSS in the Fock basis (see Chapter 3),

jΨ iD

nD0

1  λ

jn, ni , (5.14)

giving at the same time the Schmidt decomposition (see Section 1.5) with Schmidt

coefﬁcient

1  λ

. These decrease exponentially with photon number n.Intu-

itively, the photon subtraction can be described by applying the photon annihilation

operator Oa upon the TMSS, corresponding to the asymptotic case of a beam splitter

with transmittance T ! 1. After photon subtraction, ( Oa˝Oa)jn, niDnjn1, n1i,

the renormalized state is

jΨ

nD0

(1  λ

)

3/2

1 C λ

(n C 1)λ

nC1

jn, ni , (5.15)

whose Schmidt coefﬁcients now decrease more slowly with increasing photon

number n. Quantifying the entanglement of the states in Eqs. (5.14) and ( 5.15)

using the logarithmic negativity (see Section 1.5) gives

(jΨ i) D log

1 C λ

1  λ

, (5.16)

(jΨ

i) D log

(1 C λ)

(1  λ)(1 C λ

)

. (5.17)

For any squeezing 0 < λ < 1, the entanglement of the TMSS state can be en-

hanced through a perfect photon annihilation operation. However, this is no longer

so straightforward, though similar conclusions can still be drawn when we replace

the pure TMSS by a mixed state corresponding to the realistic situation in the exper-

iment described below or after a lossy-channel transmission for communication;

5.5 Experiment: Entanglement Distillation 233

or when we use a beam splitter and photon detectors instead of the ideal photon

annihilation operator (see [158] for more details).

5.5

Experiment: Entanglement Distillation

5.5.1

Qubits

Although there are several experimental demonstrations of qubit entanglement

distillation [255, 257, 265], we will explain the experiment of Pan et al. [265] in de-

tail in this section. This is because the error model used in this experiment is rather

general and instructive. The original proposal for this type of entanglement distilla-

tion was made by Bennett et al. [22] and a scheme realizable with linear optics was

proposed by Pan et al. [256]. Based on that scheme, Pan et al. demonstrated qubit

entanglement distillation [265].

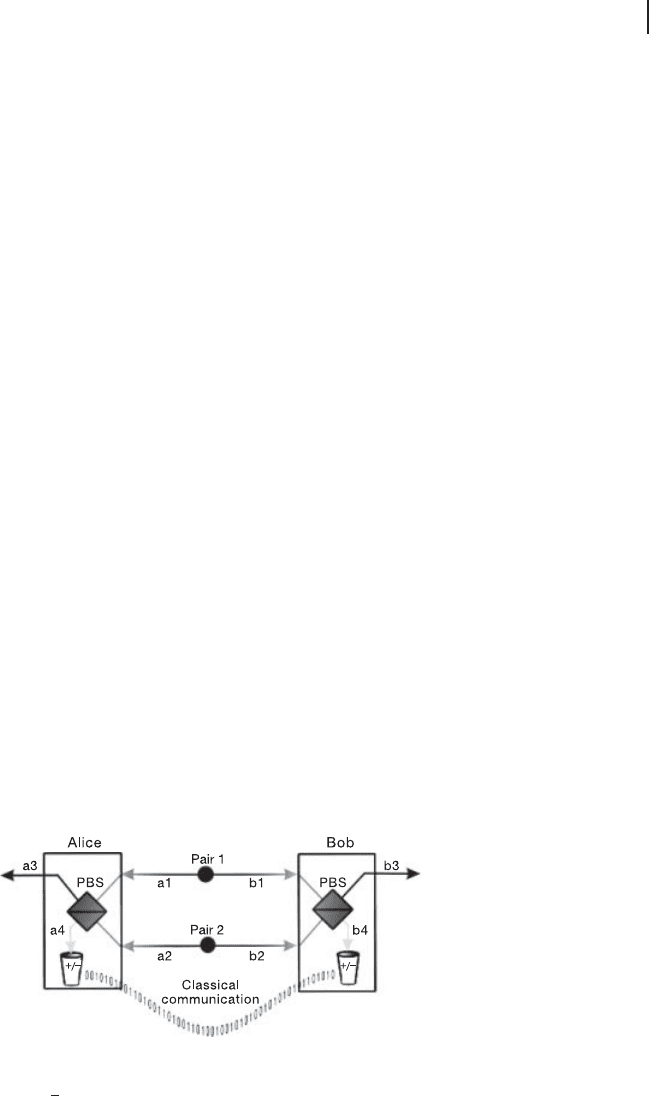
Figure 5.9 shows qubit entanglement distillation as proposed and demonstrated

by Pan et al. [256 , 265]. In this experiment, the polarization entangled state jΦ

(C)

[see Eq. (3.19)] is distilled. First, Alice and Bob share two mixed entangled pairs

a1–b1 and a2–b2 whose density operators are

O

aibi

D F

(C)

aibi

(C)

C (1  F)

()

aibi

()

, (5.18)

where i D 1, 2 denotes pair 1 or 2, jΨ

()

i is deﬁned in Eq. (3.19), and F D

hΦ

(C)

jO

aibi

jΦ

(C)

i is the ﬁdelity to the desired state jΦ

(C)

i. Then, Alice combines

photons a1 and a2 with a polarization beam splitter (PBS) and gets photons a3 and

a4. Similarly, Bob combines photons b1 and b2 with a PBS and gets photons b3

and b4. Here, only the case with photons simultaneously at a3, a4, b3, and b4 is

post-selected.

From the nature of PBS shown in Figure 5.10, photons a3 and a4 and pho-

tons b3 an d b4 have to have the same polarization in the case of photons being

Figure 5.9 Scheme for qubit entanglement distillation proposed and demonstrated by Pan

et al. [256, 265]. Photons a4 and b4 are measured with fjCi, jig basis, where j˙i D (j$i ˙

jli)/

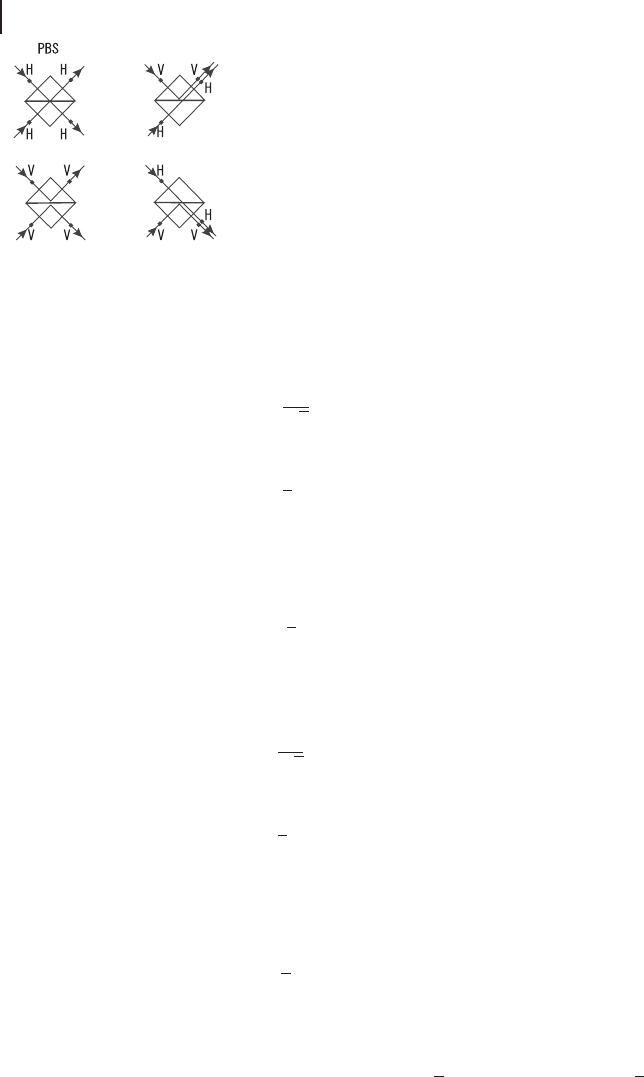
234 5 Quantum Error Correction

(a) (b)

Figure 5.10 Nature of a PBS used in the experiment [256, 265].

Two photons with horizontal (H) or vertical (V) polarization

are combined by a PBS. (a) Two photons have the same polar-

ization and (b) different polarization.

simultaneously present at a3, a4, b3, and b4. From the constraint, only the cases of

jΦ

(C)

a1b1

˝jΦ

(C)

a2b2

and jΨ

()

a1b1

˝jΨ

()

a2b2

can survive with the probability

/2 and (1  F)

/2, respectively. More explicitly,

(C)

a1b1

(C)

a2b2

(

j$i

˝j$i

Cjli

˝jli

)

(

j$i

˝j$i

Cjli

˝jli

)

(

j$i

˝j$i

Cj$i

˝jli

˝j$i

˝jli

Cjli

˝j$i

˝jli

˝j$i

Cjli

˝jli

)

(

j$i

˝j$i

Cjli

˝jli

)

, (5.19)

and

()

a1b1

()

a2b2

(

j$i

˝jli

jli

˝j$i

)

(

j$i

˝jli

jli

˝j$i

)

(

j$i

˝j$i

˝jli

j$i

˝jli

˝j$i

jli

˝j$i

˝jli

Cjli

˝jli

˝j$i

)

(

j$i

˝j$i

˝jli

Cjli

˝jli

˝j$i

)

. (5.20)

As a ﬁnal step, Alice and Bob make a polarization measurement with fjCi, jig

basis for photons a4 and b4 where jCi D (j$iCjli)/

2andji D (j$ijli)/

Then, Alice and Bob make a classical communication to compare the measurement

5.5 Experiment: Entanglement Distillation 235

results and ﬁnish the distillation. Here, they use the following relations:

j$i

˝j$i

Dj$i

jCi

Cji

˝j$i

jCi

Cji

j$i

˝j$i

˝jli

Dj$i

jCi

Cji

˝jli

jCi

ji

jli

˝jli

˝j$i

Djli

jCi

ji

˝j$i

jCi

Cji

jli

˝jli

Djli

jCi

ji

˝jli

jCi

ji

. (5.21)

For example, if both Alice and Bob get C and make it sure with classical commu-

nication, the state of photons a3 and a4 becomes the mixed state of jΦ

(C)

a3b3

and

jΨ

(C)

a3b3

with the density operator

O

a3b4

D F

(C)

aibi

(C)



1  F



(C)

aibi

(C)

, (5.22)

where F

D F

/(F

C (1  F )

). In the case of F > 0.5, which means the ﬁdelity

to jΦ

(C)

i is not bad at the very beginning, F

> F and the distillation is accom-

plished.

For the case of the other measurement results like , C,andC,Aliceand

Bob can make a distillation in principle, but they have to make a feedforward like

teleportation and quantum error correction [22, 256]. In the experiment of Pan

et al., they just post-selected the case of CC for eliminating feedforward [265].

Figure 5.11 shows the experimental setup for qubit entanglement distillation

demonstrated by Pan et al. [265]. By using the method explained in Section 3.1.3.1,

they created two pairs of polarization entangled photons a1–b1 and a2–b2 in the

state jΦ

(C)

i. Both pairs suffer from decoherence or error which is imposed with

halfwaveplatesshowninFigure5.11.

Figure 5.12 shows the experimental results. In the cases of Figure 5.12a,b, the

half-wave-plate axis was oriented at 14

which corresponds to the initial ﬁdelity

F D 0.75, and the results were consistent with the theory explained above. Here,

we can check it with the following relations:

(C)

(

j$i

˝j$i

Cjli

˝jli

)

(

jCi

˝jCi

Cji

˝ji

)

, (5.23)

()

(

j$i

˝jli

jli

˝j$i

)

(

jCi

˝ji

ji

˝jCi

)

. (5.24)

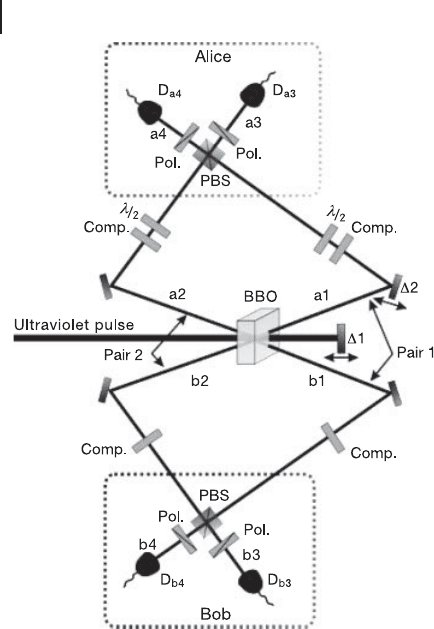
236 5 Quantum Error Correction

Figure 5.11 Experimental setup for qubit entanglement distillation demonstrated by Pan

et al. [265]. λ/2: half wave plate for imposing an error.

Figure 5.12c,d shows the results of entanglement distillation (integration time

was about 0.5 h). We can check the success of distillation with Eqs. (5.23) and (5.24)

again.

5.5.2

Qumodes

Although there are several experimental demonstrations of CV entanglement

distillation [250–252, 259], we will explain the experiment performed by Hage

et al. [252] in detail. This is because this CV experiment is very similar to qubit

entanglement distillation explained in Section 5.5.1.

As shown in Section 3.2.3.1, a CV (two-party) entangled state can be created with

two squeezed vacua and a half beam splitter. More precisely, one can create a CV

entangled state with only one squeezed vacuum and a half beam splitter which can

be regarded as an asymmetric state with squeezing parameters with r

> 0and

D 0. In the experiment of Hage et al., this type of entangled state is distilled

when phase noise is present in each beam.

5.5 Experiment: Entanglement Distillation 237

(a)

(d)

(c)

(b)

Figure 5.12 Experimental results for qubit

entanglement distillation demonstrated by

Pan et al. [265]. H: $,V:l. (a, b) before dis-

tillation (a) fj$i, jlig basis measurement,

(b) fjCi, jig basis measurement. (c, d) after

distillation (c) fj$i, jlig basis measurement,

(d) fjCi, jig basis measurement.

Figure 5.13 shows the experimental setup for CV entanglement distillation

demonstrated by Hage et al. [252]. Two optical parametric ampliﬁers (subthreshold

optical parametric oscillators) create two independent squeezed light beams. These

two beams are divided into two beams by half beam splitters BS

E,1

and BS

E,2

,re-

spectively, and two pairs of entangled light beams are created. The two pairs of

entangled light beams are shared by Alice and Bob. Phase noises are imposed on

the entangled light beams as decoherence.

For distillation, ﬁrst, Alice and Bob locally combine their parts of entangled pairs

with half beam splitters BS

D,A

and BS

D,B

. Then, they make local measurements on

amplitude quadratures X

T,A

and X

T,B

respectively for one of the output of the beam

splitters with balanced homodyne detectors BHD

T,A

and BHD

T,B

.AliceandBob

make a classical communication to chose trigger condition for distillation which

satisﬁes

T,A

C X

T,B

j < Q , (5.25)

where Q is a certain threshold selected in the experiment. Here, we should recall

that a sufﬁcient condition for entanglement is



∆



COx





∆



Op



< 1 . (5.26)

This condition would be satisﬁed with a certain value of Q in Eq. (5.25) [266]. Note

that this procedure is very similar to the qubit distillation protocol explained in

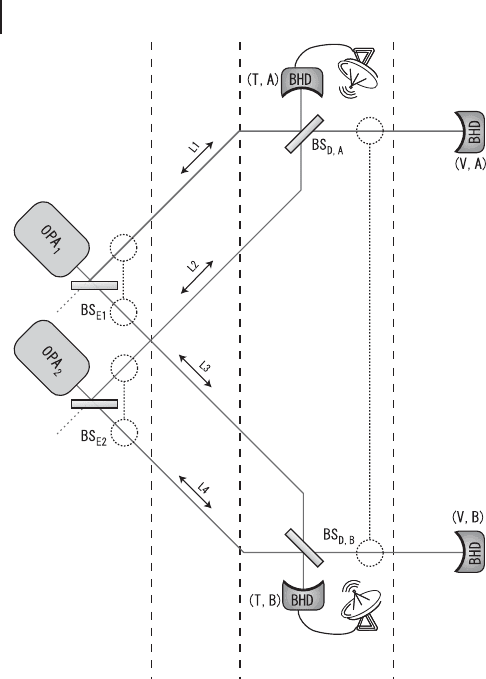
238 5 Quantum Error Correction

Entangled-

state

preparation

Noisy

trans-

mission

Verification/

downstream

application

Distillation/

purification

Figure 5.13 Experimental setup for CV entanglement distillation demonstrated by Hage

et al. [252]. δ

: ﬂuctuation of path length, BHD: balanced homodyne detector, OPA: optical

parametric oscillator (squeezer), BS: half beam splitter.

Section 5.5.1 where Alice and Bob make local measurement and classical commu-

nication.

As a ﬁnal step of distillation, Alice and Bob select those times when Eq. (5.25)

is satisﬁed and so the other outputs of the half beam splitters BS

D,A

and BS

D,B

be-

come a distilled pair. The outputs are measured with balanced homodyne detectors

BHD

V,A

and BHD

V,B

to verify distillation.

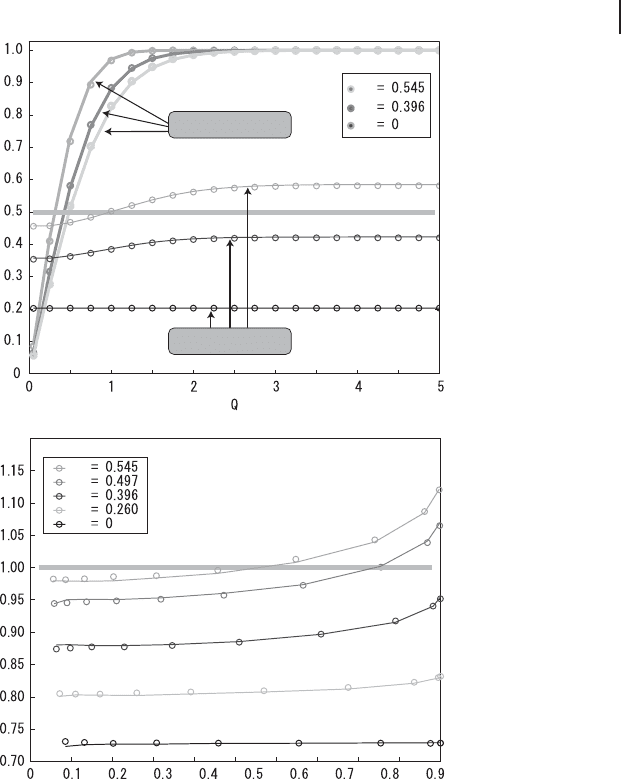
Figure 5.14 shows the results of distillation [252]. The results show the success

of entanglement distillation with a certain threshold value Q when the phase ﬂuc-

tuation is up to σ D 0.545. Here, total variance of (X

V,A

C X

V,B

)and(P

V,A

 P

V,B

)

below unity means the existence of entanglement according to the inequality in

Eq. (5.26).

In the remainder of this section, we will describe another example of a CV en-

tanglement distillation experiment which was performed by Takahashi et al. [264].

In this experiment, Gaussian entangled states are distilled through non-Gaussian

5.5 Experiment: Entanglement Distillation 239

(a)

(b)

Variance

Success rate

Success rateVarianceTotal variance/degree of separability

Figure 5.14 Experimental results for CV en-

tanglement distillation demonstrated by Hage

et al. [252]. (a) Variance of (X

V,A

C X

V,B

)and

corresponding success rates versus thresh-

old value Q for different strengths of the

phase ﬂuctuation σ. (b) The total variance of

V,A

C X

V,B

)and(P

V,A

 P

V,B

) plotted against

the success rate. The total variance below one

means the existence of entanglement.

operations. Therefore, we h ave the converse situation compared with Hage’s ex-

periment described above, where non-Gaussian entangled states were distilled by

means of Gaussian operations.

In order to apply an appropriate non-Gaussian measurement such as photon

counting upon a Gaussian state, we need to be able to perform the whole experi-

ment in the time domain. This is different from the more traditional CV experi-

ments which were mainly conducted in the frequency domain; recall our discus-