Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing

Подождите немного. Документ загружается.

200 4 Quantum Teleportation

In the real experiment, however, the OPO output modes suffer from inevitable

losses and hence deviate from the ideal case. In particular, the mixedness of the

states renders the experimental procedure more complicated than for the above

discussion based on pure states. Now, the states are no longer minimum uncer-

tainty states, having the uncertainty product h(∆ Ox

i,ii

)

ih(∆ Op

i,ii

)

i > 1/16. This

gives rise to the asymmetry between squeezing and antisqueezing and leads us

to optimize two parameters of squeezing and antisqueezing for minimization of

the additional noise. This is again in contrast to quantum teleportation: in princi-

ple, the antisqueezing terms are canceled out and the asymmetry never affects the

performance of teleportation.

To evaluate the performance of telecloning, we use a ﬁdelity which is deﬁned

as F Dhψ

jO

out

jψ

i [210, 211]. The classical limit for the case of coherent state

inputs is derived by averaging the ﬁdelity for a randomly chosen coherent input;

the classical limit of the averaged ﬁdelity F

is 1/2 [210, 212]. In a real experiment,

it is impossible to take an average over the entire phase space. However, if the

gains of the classical channels that are deﬁned as g

x1, x 2

DhOx

1,2

i/hOx

i and g

p1,p 2

hOp

1,2

i/hOp

i are unity g

x1, x 2

D g

p1,p 2

D 1, the averaged ﬁdelity is identical to the

ﬁdelity for a particular coherent state input (F

D F). This is because the ﬁdelity

with unity gains can be determined by only the variances of the t elecloned states,

which is independent of the amplitude of the coherent state input. Experimental

adjustments of g

D g

D 1 is performed in the manner of [204]. The ﬁdelity for a

coherent state i nput and g

D g

D 1 can be written as [203]

F D 2

1 C 4

(

∆ Ox

1,2

)

Eih

1 C 4

(

∆ Op

1,2

)

. (4.23)

From the above discussion, if we measure h(∆ Ox

1,2

)

i and h(∆ Op

1,2

)

i of the outputs

for a coherent state input and get F > 1/2, then we can declare the success of

telecloning of coherent state inputs. Note that the ﬁdelity of the optimal telecloning

of coherent state inputs is 2/3 [221], which can be calculated from the parameters

of the ideal case mentioned above.

By using Eq. (4.23) and experimental results of squeezing/antisqueezing, we can

calculate the expected ﬁdelities of the telecloning experiments. Figure 4.17a shows

the typical pump power dependence of squeezing and antisqueezing of the out-

put of the OPOs. Here, the OPO cavities contain potassium niobate crystals inside

as nonlinear mediums and are pumped with frequency doubled outputs of con-

tinuous wave Ti:sapphire laser at 860 nm. In order to minimize the asymmetry

of squeezing without sacriﬁcing the level of squeezing, Koike et al. selected mir -

rors with a reﬂectivity of 12% for the output coupl ers of the OPOs [220]. With

Eqs. (4.21)–(4.23) and these experimental results, the expected ﬁdelities of the tele-

cloning experiments were calculated and are plotted in Figure 4.17b. From these

calculations, Koike et al. set the pump power at 60 mW, at which they expected the

best ﬁdelity to be around 0.6.

Figure 4.18 shows the results of quantum telecloning from Alice to Bob and

Claire. The experiments for two types of input states were performed. One is a vac-

uum and the other is a coherent state that is created by applying electro-optic mod-

4.2 Qumode Quantum Teleportation 201

-6

-4

-2

(a)

(b)

0.02 0.04 0.06 0.08 0.1 0.12 0.14

Squeezing(dB)

Pump Power(W)

0.02 0.04 0.06 0.08 0.1 0.12 0.14

Pump Power(W)

0.5

0.55

0.6

0.65

Fidelity

Figure 4.17 (a) Pump power dependence of

squeezing and antisqueezing of the output of

OPO

[220]. The squeezing and antisqueez-

ing are measured at 1 MHz. Visibility at a half

beam splitter for homodyne measurement

is about 0.95 and quantum efﬁciency of the

detector is more than 99%. (b) Calculated

ﬁdelities from the squeezing and antisqueez-

ing [220].

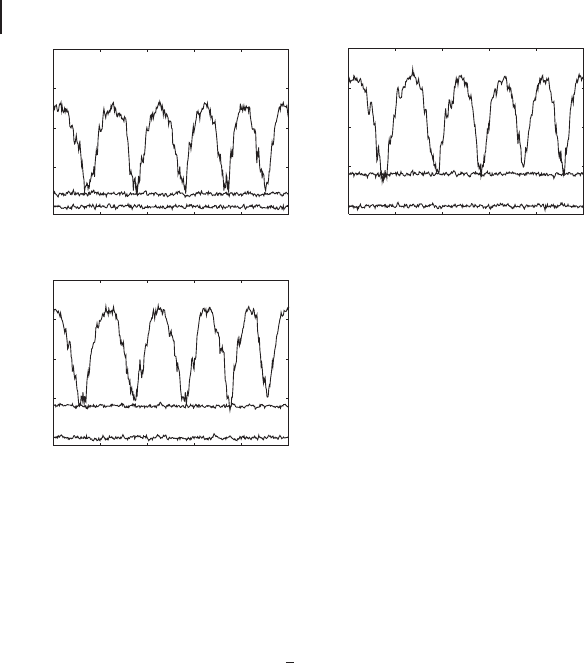
ulation to a very weak carrier beam. In Figure 4.18a, trace ii shows the result of Al-

ice’s p-quadrature measurement for a vacuum input which corresponds to h( Op

)

where Op

D ( Op

(0)

COp

2. Note that hOp

(0)

iDhOp

iD0; thus h( Op

)

iDh(∆ Op

)

and the variance of a coherent state input h(∆ Op

)

i is equivalent to h( Op

)

i because

a vacuum state is a coherent state with zero amplitude. The noise level is 2.1 dB

higher compared to the vacuum noise level h(∆ Op

(0)

)

iD1/4. This additional noise

comes from “entangled noise” Op

. The noise will be canceled to some extent with

the entanglement between Alice and Bob, and between Alice and Claire. Trace iii

in Figure 4.18a shows the case for a coherent state input with the phase scanned.

The bottom of the trace shows the same level as that of trace ii within the experi-

mental accuracy. This fact is consistent with the above discussion on the variance

of a coherent state input. The top of trace iii corresponds to the amplitude of the

measured state and is 3 dB lower than that of the input state because of the input

half beam splitter. Figure 4.18b,c shows the measurement results of the telecloned

202 4 Quantum Teleportation

(i)

(ii)

(iii)

(i)

(ii)

(iii)

(a)

(c)

(b)

0.02 0.04 0.06 0.08 0.1

(dB)

Time (s)

0 0.02 0.04 0.06 0.08 0.1

(dB)

Time (s)

0.02 0.04 0.06 0.08 0.1

Time (s)

(i)

(ii)

(iii)

Figure 4.18 Quantum telecloning from Al-

ice to Bob and Claire [220]. All traces are

normalized to the corresponding vacuum

noise levels. (a) Alice’s measurement re-

sults for p quadrature (x quadrature is not

shown). Trace i, the corresponding vacu-

um noise level h(∆ Op

(0)

)

iD1/4. Trace

ii, the measurement result of a vacuum in-

put h( Op

)

i where Op

D ( Op

(0)

COp

Trace iii, the measurement result of a co-

herent state input h( Op

)

i with the phase

scanned. (b, c) The measurement results of

the telecloned states at Bob (b) and Claire (c)

for p quadratures (x quadratures are not

shown). Trace i, the corresponding vacuum

noise levels. Trace ii, the telecloned states

for a vacuum input h(∆ Op

1,2

)

i. Trace iii, the

telecloned states for a coherent state input.

The measurement frequency is centered at

1 MHz, and the resolution and video band-

widths are 30 kHz and 300 Hz, respectively. All

traces except for trace iii are averaged twenty

times.

states. Traces ii in the ﬁgures show the results for a vacuum input which corre-

spond to h(∆ Op

1,2

)

i. The noise level for Clone 1 is 4.06 ˙0.17 dB and that for Clone

2is4.03˙ 0.15 dB. The x quadratures were also measured, which correspond to

h(∆ Ox

1,2

)

i and were 3.74 ˙ 0.15 dB for Clone 1 and 3.79 ˙0.15 dB for Clone 2 (not

shown in the ﬁgures). Note that the telecloned states have the same mean ampli-

tude as that of the input inferred from Alice’s measurement, which is consistent

with the unity gains of classical channels.

By using the measurement results of h(∆ Ox

1,2

)

i and h(∆ Op

1,2

)

i,theﬁdelityof

Eq. (4.23) was calculated. Both of the values were 0.58 ˙ 0.01 and greater than the

classical limit of 0.5. Thus, one can declare the success of 1 ! 2 telecloning of

coherent states. Moreover, these results are operational evidences of the existence

of the tripartite entanglement. The slight discrepancies from the expected ﬁdelities

are attributed to the ﬂuctuation of phase locking of the system.

4.2 Qumode Quantum Teleportation 203

4.2.3

Experiment: Qumode Teleportation Network

Quantum teleportation [17] is one of the remarkable manifestations of quantum

physics as mentioned before. In the scheme of quantum teleportation, one can

transport an unknown quantum state from one location to another without send-

ing the quantum state itself. So far, several experiments of quantum teleportation

have been demonstrated [177, 194, 203, 204, 215, 223–225]. Quantum teleportation

is, of course, a bipartite quantum protocol, but the scheme of quantum teleporta-

tion is extendable to a multipartite quantum protocol which is called a quantum

teleportation network [161]. In the quantum teleportation network, more than two

parties are connected on the network, and a member in the network can transport a

quantum state to the other members. Multipartite quantum protocols l ike this will

be fundamental components for larger-scale quantum communication and quan-

tum computation.

In this section, we will illustrate an experiment of a tripartite quantum teleporta-

tion network for continuous variables demonstrated by Yonezawa et al. [222]. Quan-

tum entanglement shared by three parties enables teleportation between any two

of the three parties with the help of the other. In the experiment, Yonezawa et al.

demonstrated teleportation of a coherent state between three different pairs in the

tripartite network.

A quantum teleportation network is a quantum communication network linked

by quantum teleportation. For example, in a tripartite network, three parties (we

call Alice, Bob and Claire) are connected on the network in which they are spa-

tially separated and previously share GHZ-type tripartite entanglement. They can

only use local operations and classical channels to communicate with each other.

In principle, they need not even know where the others are as long as they can

communicate through the classical channels. On these conditions, they exchange

a quantum state. Here, the quantum state to be teleported is that of an electromag-

netic ﬁeld mode. We use the Heisenberg picture to describe an evolution of the

quantum state in this section as well.

In some respects, a quantum teleportation network is similar to bipartite quan-

tum teleportation. In both schemes, the parties share quantum entanglement, and

send a quantum state using local operations and the classical channels. However,

the properties of tripartite entanglement make it different from the bipartite tele-

portation in other respects.

If Alice sends a quantum state to Bob, what role does Claire play? Recall that the

three parties are in the tripartite entangled state. The third party Claire also has a

quantum correlation with the other parties. Thus, Alice and Bob need Claire’s infor-

mation to succeed in teleportation. In other words, Claire can control the transfer of

the quantum state from Alice to Bob by restricting their access to her information.

This is a clear manifestation of GHZ-type tripartite entanglement.

GHZ-type tripartite entangl ement for continuous variables can be generated

by using three squeezed vacuum states and two beam splitters as shown in Sec-

tion 3.2.3.3 [161, 188]. In the limit of inﬁnite squeezing, the state is the CV ana-

204 4 Quantum Teleportation

logue [161, 188] of G reenberger–Horne–Z eilinger (GHZ) state [140]. The CV GHZ

state is a maximal ly entangled state and a simultaneous eigenstate of zero total mo-

mentum (p

D 0) and zero relative positions (x

x

D 0 i, j D 1, 2, 3).

The entanglement properties of the GHZ state are very fragile under partial losses

of a state. For example, if one of the three subsystems is traced out, the remain-

ing state ( O

, O

) is completely unentangled [141]. Thus, without Claire’s

information, the quantum entanglement between Alice and Bob vanishes, and

quantum teleportation is no longer possible.

In a real experiment, a maximally entangled state is not available because of

ﬁnite squeezing and inevitable losses. We can still obtain, however, a fully insepa-

rable tripartite entangled state (a state none of whose subsystems can be separated)

as shown in Section 3.2.3.3 [188]. An entangled state generated by three highly-

squeezed vacuum states still behaves like the GHZ state. The properties of the

state are fragile under partial losses of the state. In this case, Claire can completely

determine success or failure of quantum teleportation between Alice and Bob.

In contrast, even if three weakly-squeezed vacuum states are used, the state is a

fully inseparable tripartite entangled state, but the remaining bipartite state after

tracing out one of the three subsystems is still entangled [165], which is similar to

the case of telecloning in the previous section. In this case, after tracing out one

subsystem (e.g., mode 3), the variance h[∆( Ox

Ox

)]

iCh[∆( Op

COp

)]

iis still below

unity [165] and shows the presence of bipartite entanglement between modes 1

and 2. If we use such a state, we will succeed in teleportation even without Claire’s

information, although teleportation ﬁdelity is lower than the case with her infor-

mation which is again similar to the case of telecloning. In order to control success

or failure of teleportation, we need to use three highly-squeezed vacuum states.

There is another important point to be made when we develop bipartite quantum

teleportation into a tripartite quantum teleportation network. Only if we use a fully

inseparable tripartite entangled state, can we succeed in teleportation between an

arbitrary pair in the network. Namely, each party can play any of the three roles: a

sender, a receiver and a controller. Note that if we use a partially entangled state,

we may succeed in teleportation for a particular combination of the sender, the re-

ceiver and the controller, but may fail for other combinations. From this point of

view, a truly tripartite quantum protocol is deﬁned as a protocol that succeeds only

if a fully inseparable (GHZ-type) tripartite entanglement is used. In order to verify

success of a truly tripartite quantum protocol, we need to succeed in teleportation

for at least two different combinations [165, 188]. For example, the experiment by

Jing et al. [226], a controlled dense coding for a particular combination, only shows

partial success and is not sufﬁcient for the demonstration of a truly tripartite quan-

tum protocol. I n the experiment presented here, quantum teleportation for three

different combinations are demonstrated.

Here, we illustrate the procedure of our quantum teleportation network experi-

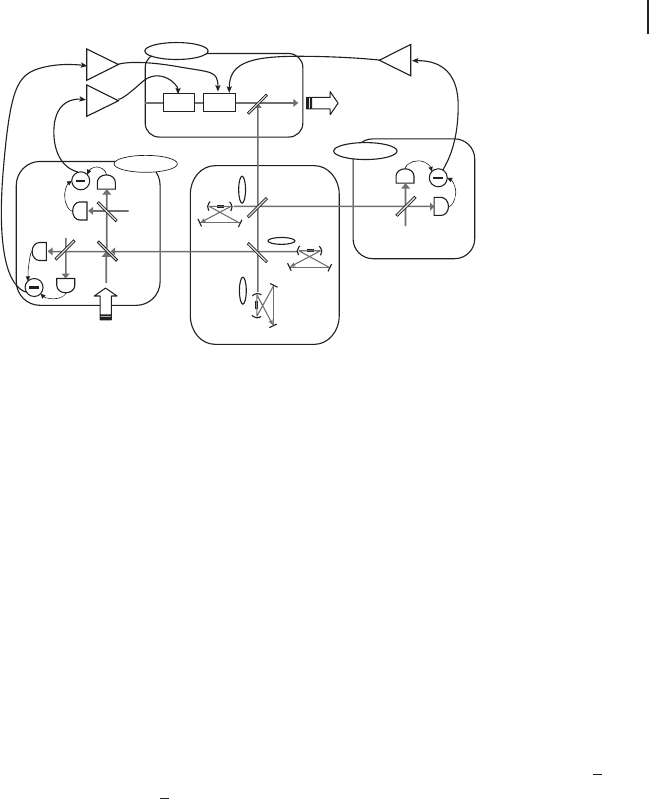
ment. Figure 4.19 shows the schematic of the experimental setup. Tripartite entan-

gled states [188] are distributed to Alice, Bob and Claire. We represent the operators

for each mode as ( Ox

, Op

)(i D A, B, C) in the Heisenberg representation. We ﬁrst

4.2 Qumode Quantum Teleportation 205

OPO1

OPO2

OPO3

Tripartite entanglement

source

Claire

Bob

Output

Alice

Input

coherent state

1:2BS

1:1BS

(x , p )

1:99 BS

1:1BS

Figure 4.19 The experimental setup for the

quantum teleportation from Alice to Bob un-

der the control of Claire [222]. In order to gen-

erate quadrature squeezed vacuum states, we

use subthreshold optical parametric oscilla-

tors (OPOs) with a potassium niobate crystal.

An output of CW Ti:sapphire laser at 860 nm

is frequency doubled in an external cavity. The

output beam at 430 nm is divided into three

beams to pump three OPOs. The pump pow-

ers are about 50 mW. Three squeezed vacuum

states are combined at two beam splitters

with relative phases locked. Three outputs of

the two beam splitters are in a tripartite entan-

gled state and sent to three parties, Alice, Bob

and Claire. The input state is a coherent state

and an optical sideband at 1 MHz.

consider the teleportation with the combination of sender Alice, receiver Bob, and

controller Claire.

First, Alice performs a joint measurement or so-called “Bell measurement” on

her entangled mode ( Ox

, Op

) and an unknown input mode ( Ox

, Op

). In the exper-

iment, the input state is a coherent state and an optical sideband of CW 860 nm

carrier light. The Bell measurement instrument consists of a half beam splitter

and two optical homodyne detectors, which is the same as the case of teleporta-

tion. Two outputs of the half beam splitter are labeled as Ox

D ( Ox

Ox

2and

D ( Op

COp

2 for relevant quadratures. The output powers of homodyne

detectors are measured with a spectrum analyzer.

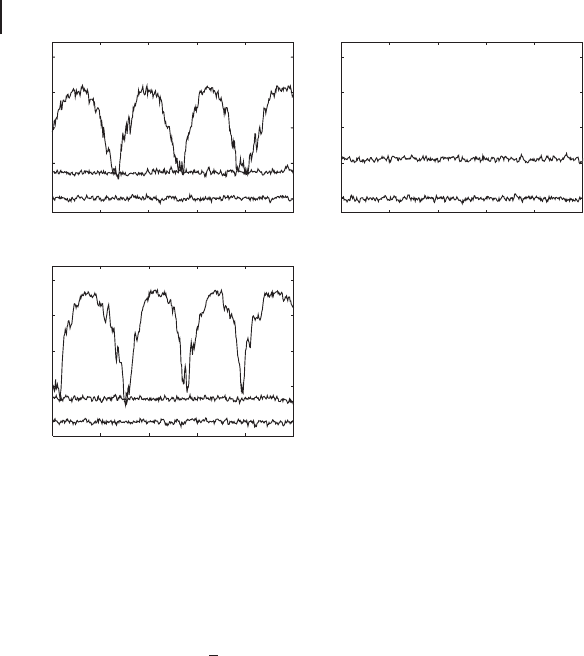
Figure 4.20a shows the measurement result of

( Op

)

at Alice (

( Ox

)

is not

shown). The visibility between the input modes and the local oscillators of Alice’s

homodyne detectors are both 0.99. The visibilities between the other modes are

about 0.97. The quantum efﬁciency of the photodiode is 0.998 at 860 nm. In Fig-

ure 4.20a, the noise level of a vacuum input

(∆ Op

)

(the variance of Op

)is3.7dB

compared to the corresponding vacuum noise level

(∆ Op

(0)

)

while the noise lev-

el for x quadrature is 2.1 dB (not shown). The measured noise levels for x and

p quadratures are asymmetric. This is because tripartite entanglement is gener-

ated by two x and one p quadrature squeezed vacuum states. For example, the

variances of the mode A are described

(∆ Ox

)

D (2e

2r

C e

)/12,

(∆ Op

)

2r

C 2e

)/12, respectively [188] (here, r is a squeezing parameter for the same

206 4 Quantum Teleportation

(dB)

(i)

(ii)

(dB)

(i)

(ii)

(iii)

(dB)

(i)

(ii)

(iii)

(a)

(c)

(b)

0.02 0.04 0.06 0.08 0.1

Time (s)

0.02 0.04 0.06 0.08 0.1

Time (s)

0.02 0.04 0.06 0.08 0.1

Time (s)

Figure 4.20 Quantum teleportation from Alice

to Bob under the control of Claire [222]. All

traces are normalized t o the corresponding

vacuum noise levels. (a) Alice’s measure-

ment results for p quadrature (x quadrature

is not shown). (i) The corresponding vacuum

noise level

(∆ Op

(0)

)

D 1/4. (ii) The mea-

surement result of a vacuum input

( Op

)

where Op

D ( Op

(0)

COp

2. Note that

(0)

DhOp

iD0thus

( Op

)

(∆ Op

)

and the variance of a coherent state input

(∆ Op

)

is equivalent to

(∆ Op

)

because

a vacuum state is a coherent state with ze-

ro amplitude. The noise level is 3.7 d B, while

the noise level for x quadrature is 2.1 dB (not

shown). (iii) The measurement result of a

coherent state input

( Op

)

with the phase

scanned. The measured amplitude of the in-

putbeamisabout15dBwhichis3dBlower

than the actual input because of the input half

beam splitter. (b) Claire’s measurement re-

sults for p quadrature. (i) The corresponding

vacuum noise level. (ii) The measurement re-

sult of

( Op

)

(∆ Op

)

. The noise level

is 5.7 dB. (c) The measurement results of the

teleported states for p quadrature (x quadra-

ture is not shown). (i) The corresponding

vacuum noise level. (ii) The teleported state

for a vacuum input

(∆ Op

tel

)

. Note t hat the

variance of the teleported state for a vacuum

input corresponds to that for a coherent state

input. The noise level is 3.3 dB for p quadra-

ture, while the noise level for x quadrature is

3.5 dB (not shown). (iii) The teleported state

for a coherent state input. The measured am-

plitude of the teleported state is about 18 dB

which is 3 dB higher than that of the input at

Alice. It assures that the classical channel’s

gains are almost unity. The measurement fre-

quency is centered at 1 MHz, the resolution

and video bandwidths are 30 kHz, 300 Hz, re-

spectively. All traces except for trace (iii) are

averaged ten times.

degree of three squeezing r D r

D r

). Thus, the measured noise levels at

Alice (

(∆ Op

)

and

(∆ Ox

)

)areasymmetric.

The measured values x

and p

for Ox

and Op

are sent through the classical chan-

nels with gain g

and g

, respectively. The third party Claire measures Op

of her

entangled mode. Note that Claire does not measure the x quadrature. Figure 4.20b

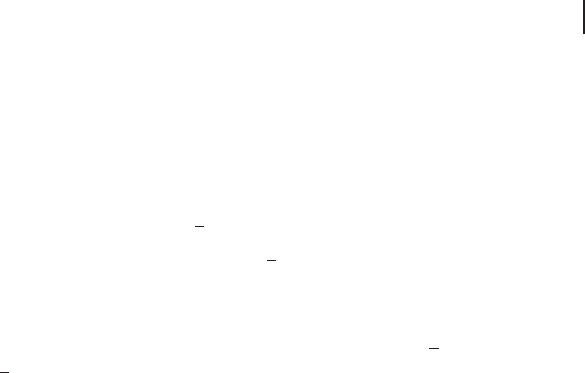
4.2 Qumode Quantum Teleportation 207

shows her measurement result

(∆ Op

)

. Claire also observes a noise and sends it

to Bob through the classical channel with gain g

The classical channel’s gains are adjusted as in the manner of [204]. The nor-

malized gains of Alice’s classical channels g

DhOx

out

i/hOx

i, g

DhOp

out

i/hOp

i are

adjusted to g

D 0.99 ˙ 0.04 and g

D 1.00 ˙ 0.03, respectively. For simplicity,

these gains are ﬁxed through the experiment and treated as unity.

Let us write Bob’s initial mode before the measurement of Alice and Claire as

DOx

 ( Ox

Ox

) 

2 Ox

DOp

C ( Op

COp

C g

) 

2 Op

 g

. (4.24)

Note that in this step, Bob’s mode remains unchanged. After measuring Ox

, Op

and

, these operators collapse and reduce to certain values. Receiving these measure-

ment results, Bob displaces his mode as Ox

!Ox

tel

DOx

, Op

!Op

tel

C g

and accomplishes the teleportation. In our experiment, dis-

placement is performed by applying electro-optical modulations. Bob modulates

a beam by using amplitude and phase modulators (AM and PM in Figure 4.19).

The amplitude and phase modulations correspond to the displacement of p and

x quadratures, respectively. The modulated beam is combined with Bob’s mode

( Ox

, Op

) at a 1/99 beam splitter, which is also the same procedure as in the telepor-

tation experiment.

The teleported mode becomes

tel

DOx

 ( Ox

Ox

tel

DOp

C ( Op

COp

C g

) . (4.25)

In the i deal case, total momentum Op

COp

and relative position Ox

Ox

have zero-eigenvalues p

C p

D 0andx

 x

D 0simultaneously,and

the teleported state is identical to the input state (g

D 1). In a real experiment,

however, the teleported state has additional ﬂuctuations. Without entanglement,

at least two units of a vacuum ﬂuctuation are added (g

D 0). These additional

vacuum ﬂuctuations are called two quduties [163] which must be paid for crossing

the boundary between classical and quantum domains, as mentioned before.

Figure 4.20c shows the measurement result of the teleported mode for p quadra-

ture with the gain g

D 1.02 ˙ 0.03.

The noise level of a vacuum input h(∆ Op

tel

)

i is 3.3 dB compared to the corre-

sponding vacuum noise level for p quadrature, while the noise level for x quadra-

ture is 3.5 dB (not shown). In the classical limit, the teleported state has three units

of a vacuum ﬂuctuation (one unit for the input state, the other two for quduties),

and the variances of the teleported state become 4.77 dB compared to the corre-

sponding vacuum noise level. The observed noise reduction from the classical limit

shows success of teleportation.

To evaluate the performance of teleportation, we use a ﬁdelity which is deﬁned

as F Dhψ

j

out

jψ

i [210, 211]. Although the classical limit of teleportation is

derived for the case of two parties in [212] and previous sections, it can be ap-

plied to the case of three parties [161]. In a classical case, three parties have no

208 4 Quantum Teleportation

quantum correlation with each other. Thus, the third party can not improve the

performance of teleportation beyond the classical limit. The classical limit of tele-

portation is derived by averaging the ﬁdelity for randomly chosen coherent state

input [212]. The classical limit of the averaged ﬁdelity F

is 1/2. In a real exper-

iment, however, it is impossible to take an average upon the entire phase space.

However, if the gains of the classical channels are unity g

D g

D 1 (not included

), the averaged ﬁdelity is identical to the ﬁdelity for a particular coherent state

input (F

D F) as shown in the previous section. The ﬁdelity for a coherent state

input can be written as F D 2/

1 C 4σ

where σ

Dh(∆ Ox

tel

)

i and

Dh(∆ Op

tel

)

i [161]. Note that a coherent state is a minimum uncertain state

whose variances are h(∆ Ox

(0)

)

iDh(∆ Op

(0)

)

iD1/4. In the experiment presented

here, the gains were set as g

D g

D 1, and the teleportation apparatus was

examined for a particular coherent state input.

Although the gains were set as g

D g

D 1 to estimate ﬁdelity, the third party’s

gain g

was changed. The best ﬁdelity should be obtained at the optimum gain g

is determined by the degree of the squeezing [161]. Here, the ﬁdelity is measured,

and the gain g

dependence of the ﬁdelity is examined.

The ﬁdelity calculated from the variances of the teleported state is plotted as a

function of g

in Figure 4.21a.

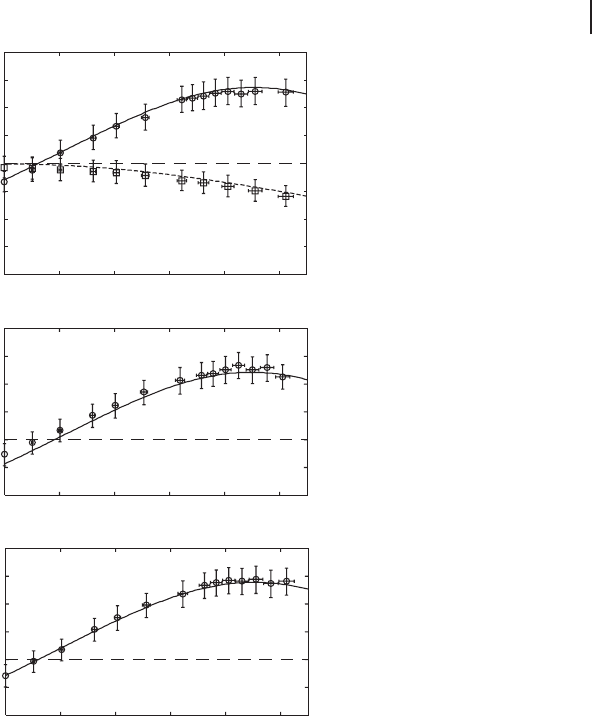
Without entanglement, the ﬁdelity is lower than 1/2. Quantum teleportation fails

and optimum g

is zero because Claire has no correlation with the other parties.

With tripartite entanglement, F D 0.63 ˙ 0.02 (g

' 0.9) is obtained, which clear-

ly shows success of quantum teleportation between Alice and Bob. At g

D 0,

however, quantum teleportation fails. This is because the tripartite entanglement

used in this experiment behaves like the GHZ state. To succeed in teleportation,

Alice and Bob need Claire’s information. If Claire does not send her information to

them, the ﬁdelity becomes even lower than that without entanglement. This clearly

shows that Claire controls success or failure of the teleportation.

Thus far, we have illustrated the experiment for the particular combination,

sender Alice, receiver Bob, and controller Claire. Note that again, one needs to

perform experiments for at least two different combinations to verify success of a

truly tripartite quantum protocol. Teleportation experiments were performed for

the other two combinations. The one combination is sender Alice, receiver Claire,

and controller Bob. The other is sender Claire, receiver Bob, and controller Alice.

The conﬁguration of the experimental setup was changed only locally while th e

global conﬁguration remains unchanged. Namely, the paths distributing the tripar-

tite entangled states remain unchanged throughout the experiment. On the other

hand, each party changes his or her setup locally according to their roles.

The gain dependence of the teleportation ﬁdelity from Alice to Claire and from

Claire to Bob are shown in Figure 4.21b and c, respectively. Both ﬁgure parts show

almost the same dependence as Figure 4.21a. This ensures that the tripartite en-

tanglement source have the same capabil ity to perform teleportation for different

combinations. The best ﬁdelities are 0.63 ˙ 0.02 and 0.64 ˙ 0.02 (g

' g

' 0.9),

respectively, which are greater than the classical limit F D 1/2 and show success

of teleportation for these two combinations. In total, three different combinations

4.2 Qumode Quantum Teleportation 209

Classical Limit

0.4

0.45

0.5

0.55

0.6

0.65

0.7

Fidelity

Classical Limit

0 0.2 0.4 0.6 0.8 1

Gain g

0 0.2 0.4 0.6 0.8 1

Gain g

0 0.2 0.4 0.6 0.8 1

Gain g

0.4

0.45

0.5

0.55

0.6

0.65

0.7

Fidelity

0.3

(a)

(b)

(c)

0.35

0.4

0.45

0.5

0.55

0.6

0.65

0.7

Fidelity

(i)

(ii)

Figure 4.21 The controller’s gain depen-

dences of the ﬁdelities [222]. (a) The ﬁdelity

of the teleportation from Alice to Bob under

the control of Claire. (i) The teleportation

without entanglement. (ii) The teleportation

with tripartite entanglement. The best ﬁdelity

0.63 ˙ 0.02 is obtained at g

' 0.9 and the

ﬁdelity is better than 1/2 in the broad range

of g

. The solid lines represent the theoreti-

cal curves calculated from the experimental

conditions. (b) The ﬁdelity of the teleportation

from Alice to Claire under the control of Bob.

The best ﬁdelity 0.63 ˙ 0.02 is obtained at

' 0.9. (c) The ﬁdelity of the teleportation

from Claire to Bob under the control of Alice.

The best ﬁdelity 0.64 ˙ 0.02 is obtained at

' 0.9. In Figure 2, each trace contains 401

measurement points, and the measurement

series are repeated 3 times. The error bars are

derived by the 1 sigma which are calculated by

401 measurement points and averaged over

three times measurements.

were demonstrated. These results show success of a quantum teleportation net-

work, that is, a truly tripartite quantum protocol.