Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing

Подождите немного. Документ загружается.

180 4 Quantum Teleportation

4.1

Qubit Quantum Teleportation

As we explained in Section 1.6, through DV quantum teleportation, an arbitrary,

unknown qubit state can be transferred using shared entanglement and classical

communication. If instead, without using shared entanglement, Alice and Bob at-

tempted to transfer the qubit state, A lice would have to measure the state in order

to gain as much information as possible and to convey this classical information

to Bob who would eventually prepare a quantum state according to that informa-

tion. This classical teleportation of an unknown qubit state achieves a ﬁdelity of

F D 2/3 at most. This value represents the boundary between classical and quan-

tum teleportation when unknown qubit states are to be transmitted [193]. Let us

now discuss various qubit teleportation experiments.

4.1.1

Experiment: Qubit Quantum Teleportation

One of the most famous experiments of qubit teleportation was performed by

Bouwmeester et al. [194]. In this section, we shall explain it in detail.

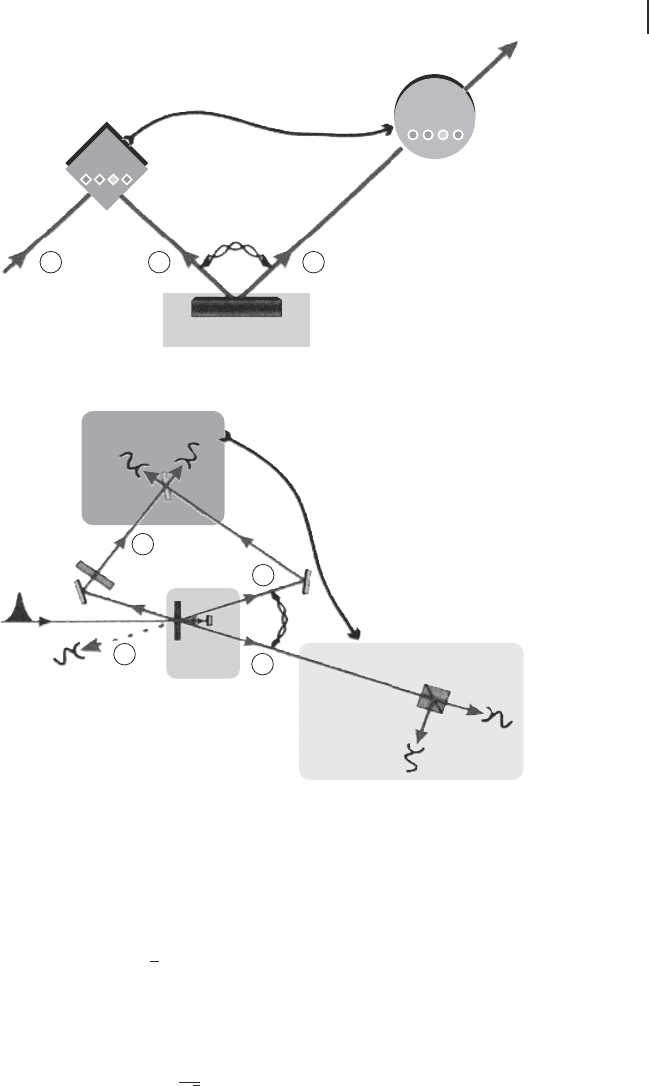
Figure 4.1 shows the scheme of qubit teleportation as done by Bouwmeester

et al. [194]. First, Alice and Bob share a polarization entangled photon pair,

jΨ

()

(

j$i

˝jli

jli

˝j$i

)

, (4.1)

which can be created by the method shown in Section 3.1.3.1.

Alice now performs a Bell measurement on the input c

j$i

C c

jli

and her

entangled photon. This Bell measurement can be understood from the following

decomposition (recall Section 1.6),

(

j$i

C c

jli

)

()

inA

(

c

 c

)

(C)

inA

(

c

C c

)

()

inA

(

C c

)

(C)

inA

(

 c

)

, (4.2)

where jΨ

(˙)

i and jΦ

(˙)

i are the Bell states deﬁned in Eq. (3.19).

In the experiment of Bouwmeester et al.,onlythecaseofjΨ

()

inA

can be detect-

ed. This is because their scheme of Bell measurement corresponds to simultaneous

detection of photons at detectors f1 and f2 as follows.

Simultaneous detection of photons at detectors f1 and f2 may be represented by

h0jOa

[195], where j, k D$, l and,



COa



, Oa



Oa



. (4.3)

4.1 Qubit Quantum Teleportation 181

BSM

EPR-

source

Teleported state

Teleported

state

ALICE

Initial

state

Initial

state

UV-pulse

Classical

information

Classical

information

“coincidence”

Entangled pair

EPR-source

BOB

Analysis

PBS

(a)

(b)

Figure 4.1 Scheme of qubit quantum teleportation demonstrated by Bouwmeester et al. [194].

(a) the concept, (b) the experimental setup.

Here, the relations of Eq. (4.3) come from a hal f beam splitter at A lice. Therefore,

h0jOa

becomes

h0jOa

h0j



COa

Oa



. (4.4)

If we neglect the probability of two photons in the input and Alice’s mode, we can

omit Oa

and Oa

in Eq. (4.4). Thus, the ﬁnal expression of h0jOa

becomes

(

inA

()

j ¤ k

0 j D k .

(4.5)

182 4 Quantum Teleportation

From this consideration, simultaneous detection of photons at detectors f1 and f2

is physically equivalent to projection onto jΨ

()

inA

With the scheme of Bell measurement, one can detect the case of jΨ

()

inA

Eq. (4.2). So when detectors f1 and f2 have simultaneous “clicks”, the overall state

of the input and an entangled photon pair of Alice and Bob in Eq. (4.2) shrinks into

jΨ

()

inA

(

c

j$i

 c

jli

)

DjΨ

()

inA

(

j$i

C c

jli

)

. (4.6)

Since we can neglect overall phase, Bob can recover the input state at his place

(mode).

Note that this scheme depends on post-selection and only the case of jΨ

()

inA

can be determined from the four Bell states jΨ

(˙)

inA

and jΦ

(˙)

inA

.Thismeans

that 3/4 of events are discarded and so the success probability is 1/4.

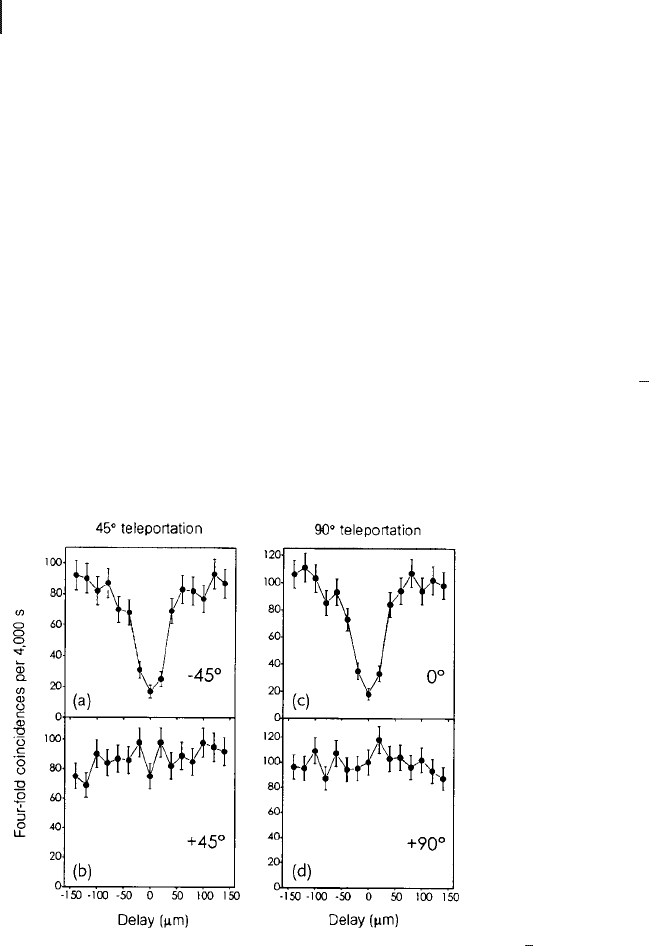
Figure 4.2 shows the experimental results for teleportation of (j$i

Cjli

and jli

demonstrated by Bouwmeester et al. [194]. It was checked with four-fold

coincidence of detection of photons at detector p, f1, f2, and d1 (d2), where “click”

at detector p shows the existence of input photon, simultaneous “clicks” at detec-

tors f1 and f2 correspond to projection onto jΨ

()

inA

, and “click” at detector d1

Figure 4.2 Experimental results of qubit

quantum teleportation demonstrated by

Bouwmeester et al. [194]. They checked four-

fold coincidence of detection of photons at de-

tector p, f1, f2, and d1 (d2). (a) and (b) reﬂect

thecaseof45

input ((1/

2)(j$i

Cjli

)),

input

(jli

). (a) and (c) are the reference experi-

ments.

1) Which is only half as big as the maximal success probability of 1/2 for a Bell measurement using

linear optics without ancilla photons and feedforward [196] (see Chapter 2).

4.1 Qubit Quantum Teleportation 183

(d2) shows the proper output. Thus, four-fold coincidences around zero delay in

Figure 4.2 mean the success of teleportation (Figure 4.2a and c are references).

Braunstein and Kimble pointed out the disadvantage of this scheme [197]. It

comes from the indistinguishability between a single photon and two photons in

the input using an on-off detector without resolving photon numbers. In the case

of two photons in the input, simultaneous detection of photons at detectors p, f1

and f2 occurs as the case of success of teleportation without entangled photons of

Alice and Bob. It is because we cannot neglect Oa

in Eq. (4.4) and then simulta-

neous detection of photons at detectors f1 and f2 no longer means projection onto

jΨ

()

inA

. Therefore, one must detect a photon at the output (detector d1 or d2) to

verify the success of teleportation. In other words, four-fold coincidence is a neces-

sary condition here for the success of teleportation. However, in the teleportation

scheme described here, a survival and a potentially further expl oitation of the tele-

ported state by avoiding post-selection is possible when photon-number resolving

detectors are used.

4.1.2

Experiment: Qubit Telecloning

Telecloning is a generalized version of teleportation where n senders send the

same quantum information to m receivers ( n-to-m telecloning) [198]. Since the no-

cloning theorem [14, 15] prohibits the receivers to have perfect clones of the input

state, the clones are approximate ones which have higher ﬁdelities to the original

than the classical limit [25]. Although complete telecloning for qubits is not re-

alized so far, “partial” telecloning is proposed by Filip [199] and demonstrated by

Zhao et al. [200]. In this section, we will explain the experiment in detail. Again,

this is also a post-selection experiment with polarization qubits (single photons).

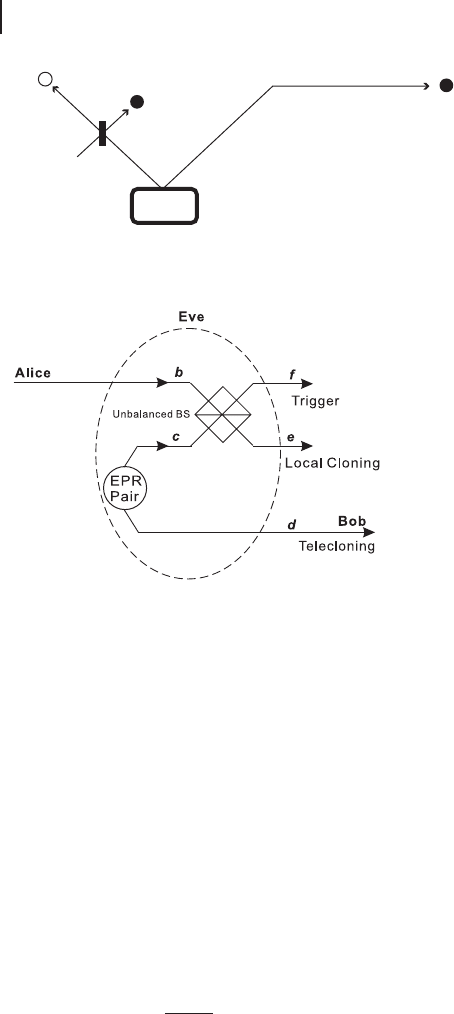
Figure 4.3 shows the proposed scheme of “partial” telecloning by Filip [199]

which was actually proposed as “partial teleportation”. Zhao et al. used an anti-

clone in Figure 4.3 as a trigger, and demonstrated the “partial” telecloning with the

scheme shown in Figure 4.4 [200]. In these schemes, an input is cloned to two,

one is a local clone and the other is distant one (teleclone). In any case, the scheme

is very similar to the one for qubit teleportation explained in the previous section.

The only difference is that a half beam splitter for Alice’s Bell measurement in

Figure 4.1 is replaced by an asymmetrical (unbalanced) beam splitter as shown in

Figures 4.3 and 4.4.

Figure 4.5 shows the experimental setup of “partial” telecloning demonstrated

by Zhao et al. [200]. In Figure 4.5, an asymmetric beam splitter is realized by a

Mach–Zehnder interferometer [201].

The asymmetric beam splitter transforms modes b and c to modes e and f as

follows,

b ! t  e Cir  f , c ! ir  e C t  f , (4.7)

2) Here, we drop the hats on annihilation operators and use “mode” and “mode operator”

synonymously.

184 4 Quantum Teleportation

ALICE

BOB

clone

distant clone

anti-clone

–

S’

Figure 4.3 Proposed scheme of “partial” telecloning as partial teleportation by Filip [199]. S, S

are clones, I is an anti-clone. R: reﬂectivity of beam splitter.

Figure 4.4 Experimental scheme of “partial” telecloning demonstrated by Zhao et al. [200].

where R D r

,1R D t

,andR is the reﬂectivity of the asymmetric beam splitter.

If an input to the cloner is in the state jψiDαjli C βj$i and the outputs from

the asymmetric beam are single photons in modes e and f, the overall state jΨ i

all

can be written as follows [199],

jΨ i

all

D α(1  2R)jli

jli

j$i

 β(1 2R)j$i

j$i

jli

 α(1  R) jli

j$i

jli

C αRj$i

jli

C β(1  R)j$i

jli

j$i

 βRjli

j$i

, (4.8)

where modes c and d are originally in the entangled state jΨ

()

deﬁned in

Eq. (3.19).

When detectors D

and D

detect photons as j$i

jli

,thestateofmodee be-

comes α(1R) jli

Cβ(12R)j$i

, whose ﬁdelity to the input jψiDαjliCβj$i

is [199],

local clone

2P(R)



(1  2R)

C (1  R)



, (4.9)

where P(R) D 13R C3R

. Similarly, when detectors D

and D

detect photons as

jli

j$i

,thestateofmodee (local clone) becomes α(1 2R)jli

Cβ(1R)j$i

whose ﬁdelity is the same as Eq. (4.9).

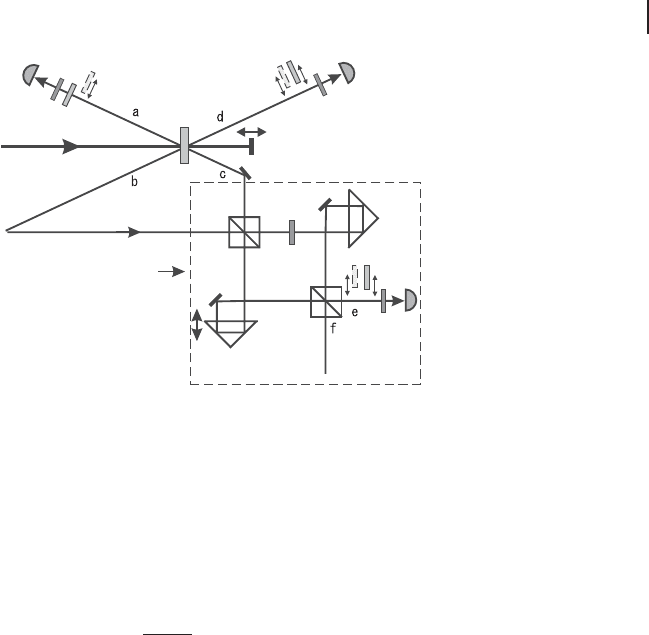
4.1 Qubit Quantum Teleportation 185

Mach-Zehnder

Interferometer

BBO

λ/4 λ/4

λ/4

Figure 4.5 Experimental setup of “partial”

telecloning demonstrated by Zhao et al. [200].

P: pola rizer, F: bandpath ﬁlter, DL: delay line,

BBO: second-order nonlinear crystal (beta-

barium borate), BS: beam splitter, D: photon

detector, λ/4: quarter wave plate. The Mach–

Zehnder interferometer acts as a variable

beam splitter. C is compensator to equalize

the path length of orthogonal polarizations.

When detectors D

and D

detect photons as jli

j$i

,thestateofmoded (dis-

tant clone or teleclone) becomes α(1R)jli

β Rj$i

, whose ﬁdelity to the input

jψiDαjli C βj$i is [199]

teleclone

2P(R)



C (1  R)



. (4.10)

Similarly , when detectors D

and D

detect photons as j$i

jli

,thestateofmode

d (distant clone or teleclone) becomes α Rjli

C β(1  R)j$i

,whoseﬁdelityis

the same as in Eq. (4.10).

Here, classical limit of the ﬁdelity for one-to-two cloning is 2/3. From Eqs. (4.9)

and (4.10), one can obtain the ﬁdelity of 5/6 for both clones with R D 1/3, which is

higher than the classical limit and thus shows the success of “partial” telecloning.

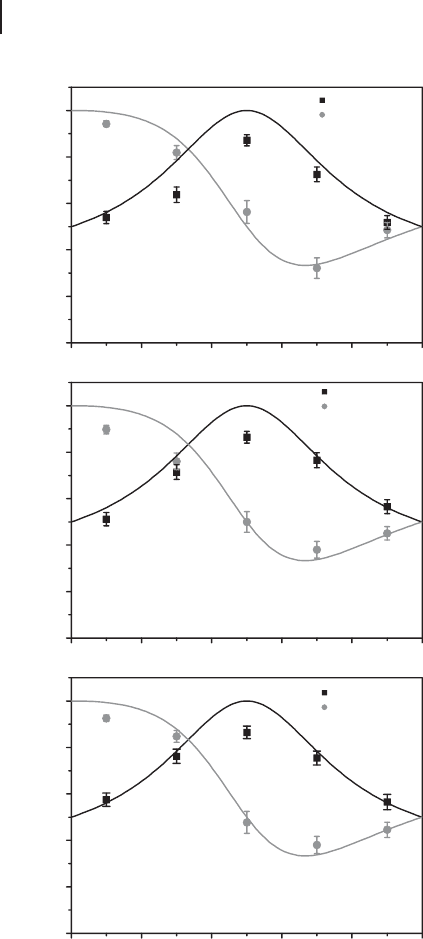
Zhao et al. checked the ﬁdelities as a function of reﬂectivity R of the asymmetric

beam splitter as shown in Figure 4.6. Theoretical curves are calculated by Eqs. (4.9)

and (4.10). The experimental results agree well with the theoretical prediction and

show the higher ﬁdelities than the classical limit of 2/3 with R D 1/3. Thus “par-

tial” telecloning is successfully demonstrated.

4.1.3

Experiment: Qubit Entanglement Swapping

With post-selection illustrated in the previous sections, entanglement swapping –

teleportation of entanglement – can be performed for polarization qubits. P an et al.

implemented this for the ﬁrst time [202]. Here, we will explain their experiment in

detail.

186 4 Quantum Teleportation

Telecloning

Local-cloning

1.0

0.8

Fidelity

0.6

0.4

0.2

0.0

1.0

0.8

Fidelity

0.6

0.4

0.2

0.0

1.0

0.8

Fidelity

0.6

0.4

0.2

0.0

0.0 0.2 0.4 0.6

Reflectivity

0.8 1.0

Telecloning

Local-cloning

Telecloning

Local-cloning

(a)

(b)

(c)

Figure 4.6 Experimental ﬁdelities of local and

telecloning as a function of the reﬂectivity R

of the asymmetric beam splitter [200]. Polar-

ization angle of polarizers P

,andP

are

(a), C45

(b), and circularly polarized with

a quarter wave plate (c). Theoretical curves

are calculated by Eqs. (4.9) and (4.10).

4.1 Qubit Quantum Teleportation 187

Bell State

Measurement

EPR-source II

EPR-source I

12 34

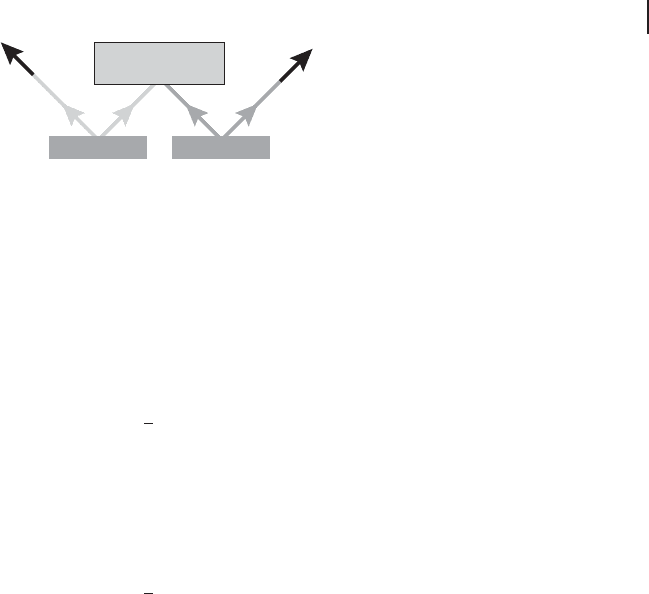
Figure 4.7 Principle of entanglement swap-

ping [202]. Two EPR sources produce two

pairs of entangled photons, pair 1–2 and pair

3–4. One photon from each pair (photons 2

and 3) is subjected to a Bell measurement.

This results in projecting the other two outgo-

ing photons 1 and 4 onto an entangled state.

Figure 4.7 shows the principle of entanglement swapping [202]. First, two EPR

sources each simultaneously emit a pair of entangled photons, pair 1–2 and pair

3–4. The overall state of photons 1–4 jΨ i

1234

is represented as follows:

jΨ i

1234

()

(

j$i

jli

jli

j$i

)

(

j$i

jli

jli

j$i

)

, (4.11)

with jΨ

()

i from Eq. (3.19). Next, a Bell measurement is performed on photons

2 and 3. After the Bell measurement, photons 2 and 3 are projected onto one of

the four Bell states jΨ

(˙)

i and jΦ

(˙)

i described in Eq. (3.19), and the overall state

jΨ i

1234

gets “rearranged” to

jΨ i

1234



(C)

()

(C)

()



. (4.12)

When we know the result of Bell measurement, the overall state shrinks to one of

the four cases as shown in Eq. (4.12). For example, in the case of jΨ

()

obtained

in the Bell measurement, the overall state shrinks to jΨ

()

jΨ

()

. In this state,

photons 1 and 4 are entangled and photons 2 and 3 are entangled. The situation is

similar for the other results of the Bell measurement, that means photons 1 and 4

are entangled and photons 2 and 3 are entangled in all cases. Thus, entanglements

in 1–2 and 3–4 are swapped, and 1–4 and 2–3 become entangled.

Figure 4.8 shows the experimental setup of entanglement swapping demonstrat-

ed by Pan et al. [202], which is very similar to the one shown in Figure 4.1 [194].

EPR sources are the same ones illustrated in Section 3.1.3.1. The trick for the Bell

measurement is the same as the one in teleportation, which is explained in Sec-

tion 4.1.1. With this trick, one can detect only jΨ

()

with simultaneous detec-

tion of photons at detectors D

and D

. Moreover, as the case of the teleportation

experiment by Bouwmeester et al. [194], simultaneous detection of four photons

at detectors D

–D

is the necessary condition for success of the experiment. To

check the entanglement between photons 1 and 4, correlation measurement was

performed by changing the polarizer angle Θ before detector D

in Figure 4.1.

Figure 4.9 shows the experimental results. Counting rates of four-fold coinci-

dence are shown as a function of polarizer angle Θ before detector D

.Sincethe

188 4 Quantum Teleportation

Figure 4.8 Experimental setup of entanglement swapping demonstrated by Pan et al. [202].

The half wave plate (λ/2) just before a polarization beam splitter was set at 22.5

.Thepolarizer

angle before detector D

was scanned.

Figure 4.9 Results of the correlation measurement to check the entanglement between photons

1and4[202].

angle of the half wave plate before the polarization beam splitter was set at 22.5

detector D

detects a C45

-polarized photon and detector D



detects a 45

polarized photon. From Figure 4.9, we can clearly see the correlation between

detectors D

and D

and between detectors D



and D

, which are the proof of

jΨ

()

i-type entanglement between photons 1 and 4. Since four-fold coincidence al-

so guarantees jΨ

()

, we can conclude that th e overall state is jΨ

()

jΨ

()

meaning success of entanglement swapping.

4.2

Qumode Qua ntum Teleporta tion

By using an optical ﬁeld, qumode quantum teleportation has been experimental-

ly realized for G aussian input states – a coherent state [177, 203–205], a squeezed

state [206], and an EPR state, for so-called entanglement swapping [205, 207]. All

4.2 Qumode Quantum Teleportation 189

these experiments are based on the well-developed techniques of optical Gaussian

operations consisting of beam splitter, phase shifting, and squeezing transforma-

tions as well as phase-space displacements and homodyne detection. Those CV

quantum protocols implemented so far operated only with Gaussian states and op-

erations. However, non-Gaussian states or non-Gaussian operations are needed to

potentially achieve universal CV quantum information processing (see Chapters 6

and 7). Quantum teleportation of a non-Gaussian state would become the next im-

portant challenge (see Chapter 8).

In Section 1.6, we presented an idealized version of CV quantum teleportation

using unphysical, inﬁnitely squeezed states. In the following reports on experimen-

tal implementations of CV quantum teleportation, of course, a realistic, physical

description must be employed. For this purpose, it is most convenient to use the

Heisenberg representation for the quadrature operators. Alternative formal isms

for CV quantum teleportation include using the Wigner [163] and the Fock repre-

sentations [208, 209]. These are also both useful to describe quantum teleportation

of non-Gaussian states (see Chapter 8).

Note that unlike the discussion in Section 1.6 on idealized CV quantum telepor-

tation, Alice does gain partial information about the input state through her Bell

measurement on the input state and one half of the ﬁnitely squeezed EPR state, and

as a consequence, perfect state transfer is no longer achievable. Criteria in order to

assess the nonclassicality of CV quantum teleportation were derived in [210–212].

4.2.1

Experiment: Qumode Quantum Teleportation

In this section, we ﬁrst explain the CV teleportation experiment demonstrated by

Furusawa et al. [203] in detail.

Figure 4.10 shows the experimental setup of CV teleportation demonstrated by

Furusawa et al. [203]. First, Alice and Bob share the EPR beams that are created

with the technique explained in Section 3.2.3.1 where two squeezed vacua with

squeezing parameter r are combined at a half beam splitter. The state of the elec-

tromagnetic ﬁeld to be teleported ( Ox

, Op

) is created by Victor, which for the exper-

iment here, is more precisely a particular set of modulation sidebands (coherent

state). The beam to be teleported is combined with Alice’s EPR beam ( Ox

, Op

)by

using a half beam splitter. This process creates states described by the quadrature

amplitudes ( Ox

, Op

)and(Ox

, Op

)where



, Op



, Op

. (4.13)

Alice measures both quadratures Ox

and Op

using two homodyne detectors and

obtains the classical results x

and p

. This measurement corresponds to a CV

3) Compared to Eq. (3.38), the number subscripts for the two EPR modes are replaced by “A” and

“B”, indicating that those beams are in Alice’s and Bob’s possession, respectively.