Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing

Подождите немного. Документ загружается.

160 3 Entanglement

A conceptually different method for creating CV graph states is based upon a

single, quadratic OPO interaction [172]. This very compact approach is a multi-

mode extension of the method for creating a two-mode squeezed state from a sin-

gle NOPO instead of using two single-mode squeezed states from two OPOs. The

sufﬁcient degree of nondegeneracy in order to obtain many qumodes for the de-

sired graph state can be achieved within a so-called frequency comb. Finally, there

are two more, very recent proposals for making arbitrarily large CV cluster states.

The ﬁrst one would employ just a single squeezer and a single C

gate which is

achieved through a temporal encoding where the OPO-squeezer and the C

gate

can be reused after each measurement step [173]. A drawback of this scheme is that

the C

gate again requires online squeezing and the need for sufﬁcient delay lines.

The former complication, however, was eliminated very recently in a variation that

uses only four ofﬂine squeezers and six beam splitters [174].

3.2.3

Experiment: Entangled Photonic Qumodes

3.2.3.1 Frequency-Domain EPR-Type State

Nonclassical, so-called Einstein–Podolsky–Rosen (EPR) correlations were origi-

nally associated with two canonically conjugate, continuous quantum variables

such as particle position and momentum, as described in the seminal paper from

1935 [23]. Ou et al. were the ﬁrst to realize these EPR correlations experimentally

in the optical setting by employing a two-mode squeezed state [156, 157]. Here, the

two-mode squeezed state can be built from two squeezed vacua using a half beam

splitter, as mentioned before. It is equivalent to the state obtainable from type-II

phase matching of a second order nonli near crystal (χ

(2)

)fortwoorthogonally

polarized (signal and idler) modes, as shown in Figure 3.17. Figure 3.18 shows the

results of the experiment in Figure 3.17.

Note that frequency sidebands at ˙Ω were used for the quadrature ﬁeld ampli-

tudes in this experiment. More precisely, in accordance to the discussion on broad-

band qumodes in Section 2.2.9, the relevant state corresponds to the electromagnet-

ic ﬁeld at frequency offset ˙Ω ˙2π f within a ﬁnite bandwidth ∆Ω  2π∆ f

about the carrier ω

(laser frequency); in other words, we have AM and FM side-

bands (recall the discussion in Section 2.1 and see Figure 2.10a).

In Figure 3.18, we have ∆

inf

X h(

 g

)

i and ∆

inf

Y h(

 g

)

with

A  A hAi, and these values were obtained from the measurement of

the photocurrent difference Φ in Figure 3.17 [156]. Here, X and Y represent the

amplitude and phase quadratures.

In Figure 3.18, the noise in Φ is plotted in

dB, and so Ψ

corresponds to unity noise (with 1 D ∆

∆

). Then, the

results show that ∆

inf

X ∆

inf

Y < 1, which is a sufﬁcient condition for entangle-

ment.

5) More precisely, these are rescaled position and momentum variables, X 

2 Ox and Y 

2 Op,

using our convention as introduced in Section 1.2.

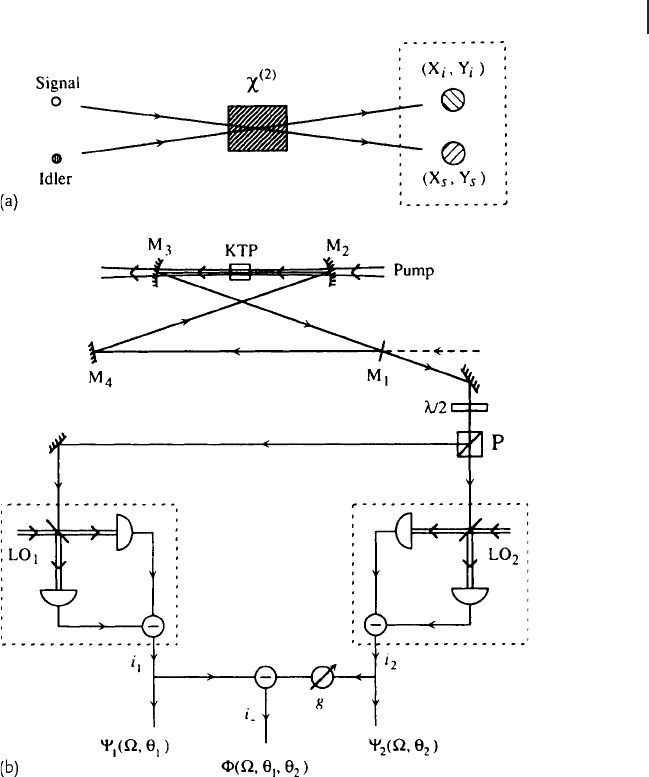
3.2 Qumode Entanglement 161

Figure 3.17 Scheme for creating an EPR-type

entangled state [156]. (a) Parametric cou-

pling through a second order nonlinear crystal

(χ

(2)

) between two orthogonally polarized

modes (Signal and Idler), (b) the experimental

setup. KTP: KTiOPO

, LO: local oscillator for

homodyne detection, i: photocurrent, g:gain,

Ψ and Φ : variances of photocurrents.

Since this signiﬁcant milestone, there have been further experimental demon-

strations of this type of EPR correlations [175–181].

3.2.3.2 Time-Domain EPR-Type State

Complementary to those experiments demonstrating EPR correlations in the fre-

quency domain, a more recent approach considers this type of CV entanglement

in the time domain. In order to incorporate those DV encodings and techniques

inherited from single-photon-based quantum protocols into a CV scheme and to

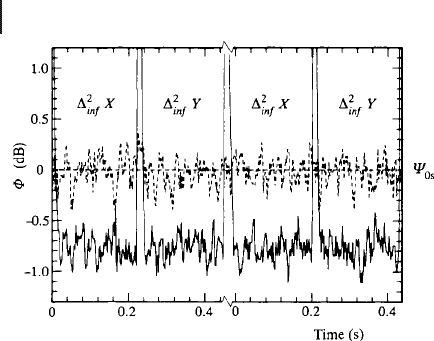
162 3 Entanglement

Figure 3.18 Results of the experiment in Figure 3.17 [156]; ∆

inf

X h(

 g

)

i and

∆

inf

Y h(

 g

)

i with

A  A hAi.Subscriptss and i denote Signal and Idler. Ψ

0 s

corresponds to the variance without quantum correlations (entanglement).

obtain those hybrid protocols discussed in detail later, it will actually be necessary

to switch from the frequency to the time domain.

As a result, quantum correlations will no longer become manifest only in sta-

tistical form. Instead, the entanglement will be resolved, in principle, down to the

level of single shots. This corresponds to a new generation of experiments that

come along with a paradigm shift from frequency to time and from statistics to single

shots. For example, as a crucial step towards CV quantum teleportation of non-

Gaussian states such as a superposition of coherent states, a time-domain two-

mode squeezed vacuum state must be employed. The shift from frequency to time

therefore starts with the entanglement resources. These will then correspond to a

kind of “fast entanglement” as opposed to the “slow entanglement” in the frequen-

cy domain and would, in principle, allow for detecting true causal EPR correlations.

In this section, the generation and characterization of a two-mode squeezed vacu-

um state in the time domain will be explained in detail according to the experiment

of Takei et al. [182]. The EPR resource is created using two squeezed vacuum states

of continuous-wave (CW) light beams from two independent subthreshold optical

parametric oscillators (OPOs). Hence, the resource state to start with is the same as

before for the creation of frequency-domain entanglement. The two squeezed vac-

uum states have well-deﬁned frequency and spatial modes, and almost the whole

frequency bandwidth of the OPO cavities is used in order to deﬁne a quantum state

in a temporal mode. So this time, using the broad bandwidth allows one to make

time-resolved measurements such as photon counting, as described below.

The time-domain experiment is rather different from the schemes in the fre-

quency domain [156, 175–180], including the experiment of Ou et al. which we had

discussed in the preceding section [156]. As those frequency-domain experiments

only deal with frequency sidebands a few MHz apart from the optical carrier fre-

quency, they are simply not compatible with photon counting measurements.

3.2 Qumode Entanglement 163

The two-mode squeezed vacuum generated by subthreshold OPOs has EPR cor-

relations within the variance spectra S

(Ω ), S

(Ω ), as usually measured in the

frequency-domain experiments.

In this case, Ω is a sideband frequency around

the fundamental wavelength (laser frequency). Now, for measuring the CW beams

through time-gated detection, we need to specify two temporal modes for which

the entangled quantum state is deﬁned. Because of the broadband correlations of

the CW beams, there is a large degree of freedom for choosing these modes. For

instance, in a teleportation experiment, the temporal modes should be chosen such

that they match the temporal mode of the input state.

A simple choice of temporal mode is a square ﬁlter of duration T.Letusdeﬁne

the ﬁltered quadrature operators,

Ox(t)dt , (3.82)

and similarly for Op

, still satisfying the usual commutation relation, [ Ox

, Op

] D

i/2. The EPR variances for two such wavepackets corresponding to two temporal

modes will be given by [183],



∆



Ox

i



2π

1

(Ω )

sin



Ω T





Ω T



dΩ , (3.83)



∆



COp

i



2π

1

(Ω )

sin



Ω T





Ω T



dΩ . (3.84)

The variances are thus ﬁltered by a sinc function, and by adjusting the integration

time T, the frequency range that contributes to the integrated correlations can be

selected. The square temporal ﬁlter is simple, but not necessarily the most suitable

choice for a given application of time-domain entanglement. Theoretical investi-

gations concerning the shape of the ﬁlter combined with photon counting experi-

ments can be found in [183, 184].

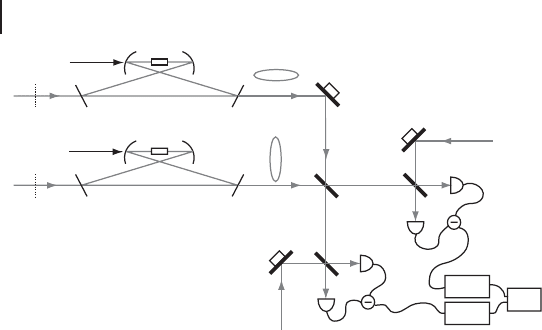
A schematic diagram of the experiment is shown in Figure 3.19 [182]. The pri-

mary source of the experiment is a CW Ti:sapphire laser at 860 nm. About 90%

of this laser light is frequency doubled in an external cavity. The output beam at

430 nm is divided into two beams in order to pump two OPOs.

A two-mode squeezed vacuum is produced by combining two squeezed vacua at

a half beam splitter (HBS). Each squeezed vacuum is generated from a subthresh-

old OPO with a 10 mm long KNbO

crystal. The crystal is temperature-tuned for

type-I noncritical phase matching. Each OPO cavity is a bow-tie-type ring cavity

consisting of two spherical mirrors (radius of curvature 50 mm) and two ﬂat mir-

rors. The round trip length is about 500 mm and the waist size in the crystal is

20 µm. An output coupler has transmissivity of 12.7%, while the other mirrors

6) S

(Ω)andS

(Ω) correspond to ∆

inf

X and ∆

inf

Y of Ou et al. [156], respectively.

164 3 Entanglement

OPO2

OPO1

ALICE

BOB

HBS

PZT

shutter

pump

ADC

Figure 3.19 Setup of the time-domain EPR

experiment [182]. OPOs: sub-threshold optical

parametric oscillators, HBS: a half beam-

splitter, PZTs: piezo-electric transducers, LOs:

local oscillators, ADC: an analogue-to-digital

converter. The ADC is an ingredient speciﬁc to

the time-domain experiment and would not be

used in a frequency-domain experiment. The

measured quantities here are amplitudes and

no more intensities, as they would be mea-

sured in a spectrum analyzer of a frequency-

domain experiment.

have a coating with extremely high reﬂectivity at 860 nm. They also have a high

transmittivity for 430 nm so that the pump beam passes the crystal only once. The

pump power is about 70 mW for each OPO. The total intracavity losses are around

2%, giving a cavity bandwidth of 7 MHz HWHM. The resonant frequency of the

OPO is locked via the FM sideband locking method [185] by introducing a l ock

beam which counterpropagates against the squeezed vacuum beam in order to

avoid any interference between the two beams.

The two output beams A and B from the HBS are measured using homodyne de-

tectorswithabandwidthof8.4MHz.TherelativephasesbetweentheEPRbeams

and the local oscillators (LOs), that is, the x and p quadratures are locked in the

following way. First, weak coherent beams that propagate along the same paths as

the squeezed states are injected into the OPOs from one of the ﬂat mirrors. These

are then used for the conventional dither and lock method. The relative phases

between the weak coherent beams and the squeezed vacua at the HBS are actively

controlled by applying feedback voltages to piezo-actuators (PZTs). The quadratures

to be detected by the homodyne detectors are al so adjusted by locking the phases

between the LOs and the injected coherent beams. However, the weak beams and

the modulation on them will contaminate the EPR correlations in some frequen-

cy ranges. Therefore, eventually we need to remove these beams and achieve the

phase locking without them.

For this purpose, an electronic circuit is introduced that holds the feedback volt-

age and keeps the phase relation for some time. Within 2 ms, the beams are blocked

using mechanical shutters before the OPOs and the EPR beams are measured

by the homodyne detectors. Each output from the detectors is sampled with an

analogue-to-digital converter (ADC) at a rate of 5  10

samples per second and

3.2 Qumode Entanglement 165

is then ﬁltered on a computer to yield a certain number of measured quadrature

values.

Before observing the EPR correlations through time-gated measurements, the

frequency bandwidth of the OPOs was estimated i n order to determine the effective

time interval of a temporal mode. Figure 3.20 shows the frequency spectra S

(Ω )

and S

(Ω ) for the measured EPR beams calculated by digital Fourier analysis on

the 50 M-sampled raw data. The EPR correlations are o bserved over the full band-

width of the OPOs. In particular, they are present at frequencies as low as 5 kHz

(a high pass ﬁlter with a cut-off of 5 kHz is used to eliminate noise at frequen-

cies close to DC). Such correlations at sufﬁciently low frequencies are essential

for the non-Gaussian photon subtraction experiments discussed later.

From these

results, one can determine a quantum state within the time interval that corre-

sponds to the inverse of the cavity bandwidth (7 MHz). Since the EPR correlations

degrade at higher frequencies, the temporal ﬁlter of Eq. (3.82) with an integration

time of T D 0.2 µs was used, yielding 10 000 points in every measurement round.

It follows from the frequency ﬁlters expressed by the sinc functions in Eqs. (3.83)

and (3.84) that we mainly select a frequency range below 5 MHz.

Now, one can explicitly compare the time-resolved quadrature values measured

for the beams A and B in every 0.2 µs time interval instead of measuring the

variances h[∆( Ox

Ox

)]

i and h[∆( Op

COp

)]

i, as done in the frequency-domain

experiments [156, 175–177]. This approach also differs from the pulsed scheme

-4

-3

-2

-1

Variances (dB)Variances (dB)

-4

-3

-2

-1

0246810

frequency (MHz)

0246810

frequency (MHz)

(a)

(b)

Figure 3.20 Fourier analysis of the 50M-sampled raw data without averaging. (a) S

(Ω )for

h[∆(Ox

Ox

)]

i.(b)S

(Ω )forh[∆( Op

COp

)]

i. Each trace is normalized to the corresponding

vacuum level.

7) In principle, it would be better to have access to even lower frequencies near zero Hz. In practice,

however, those very low frequency components below 5 kHz are often neglected, for instance, in

non-Gaussian state creation through photon subtraction [186]. Therefore, for practical purposes,

very low frequency components are not required in the EPR source, for example, when teleporting

such non-Gaussian states.

166 3 Entanglement

of [181] where the EPR beams are recombined at a beam splitter, yielding two

unentangled squeezed vacua of which one is measured by homodyne detec-

tion.

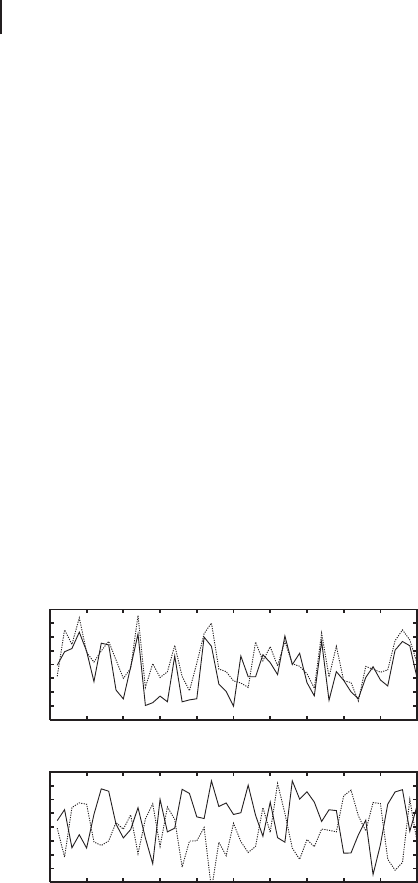
Figure 3.21 shows a typical example for the measured quadrature values with-

in a time interval of T D 0.2 µs. In this example, only 50 points are picked up.

As mentioned above, the measured values behave in such a way that the x and p

quadratures are correlated (x

' x

) and anticorrelated (p

'p

), respectively.

Hence, EPR-type correlations are veriﬁed in the time domain.

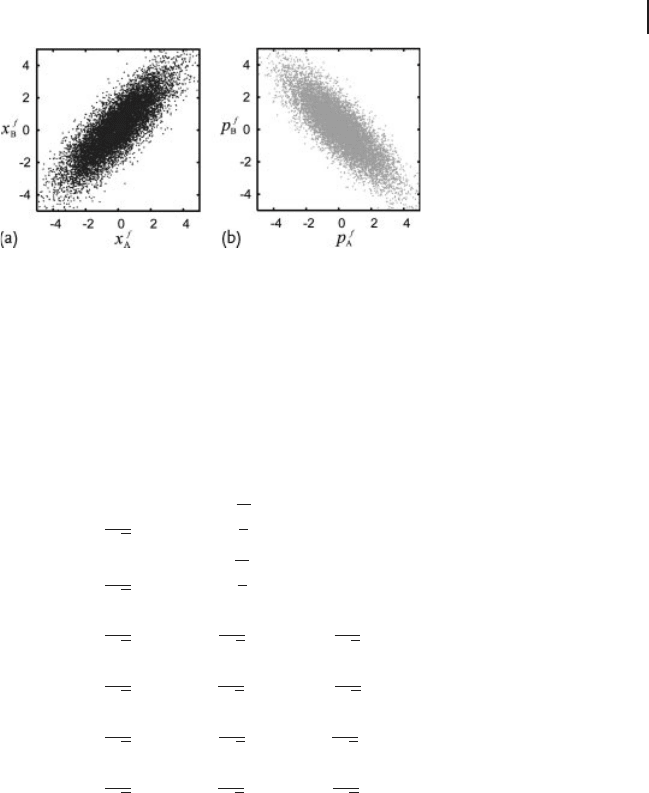
The quality of the EPR correlations can be estimated by using correlation di-

agrams like those with 10 000 points shown in Figure 3.22. When repeating the

same measurement ten times, correlations, compared to the vacuum level, corre-

sponding to h[∆( Ox

Ox

)]

iD3.30 ˙ 0.28 dB and h[∆( Op

COp

)]

iD3.74 ˙

0.32 dB are obtained. Accordingly, the sufﬁcient entanglement criteria of Duan

et al. are satisﬁed: h[∆( Ox

Ox

)]

iCh[∆( Op

COp

)]

iD0.45 ˙ 0.02 < 1.

As a result, the generated state is entangled for two temporal modes deﬁned over

the time interval T D 0.2 µs. While it is, in principle, possible to further reduce

the integration time T for faster data acquisition and hence potentially faster (quan-

tum) information processing, the EPR correlations would degrade in this case due

to the contribution of higher frequencies. Alternatively, it is also possible to obtain

correlations over a broader bandwidth by using OPOs of smaller size correspond-

ing to shorter round-trip length, or by employing waveguide crystals, for example,

periodically poled lithium niobate waveguides [187].

-4

-3

-2

-1

012345678910

Time (µs)

012345678910

Time (µs)

-4

-3

-2

-1

(i)

(ii)

(a)

(b)

Figure 3.21 Typical measured correlations.

Only 50 points are used to generate this plot.

(a) and (b) are measured quadrature values

within a time interval of T D 0.2 µsforthex

and p quadratures, respectively. In each ﬁgure,

trace (i) is for beam A, while (ii) is for beam

B. In the frequency-domain experiments, none

of these single-shot points would be actually

recorded; in order to reveal the frequency EPR

correlations, the Fourier-transformed power

spectrum is directly detected. In contrast, here

the EPR correlations are much “faster” and

can be resolved by recording a small number

of points. In principle, true causal EPR corre-

lations would even be present for every single

shot.

3.2 Qumode Entanglement 167

Figure 3.22 Correlation diagrams of 10 000 measured values for (a) x and (b) p quadratures.

3.2.3.3 GHZ-Type State

We shall describe the experiment of Aoki et al. [188] in detail. In the real experi-

ment, only ﬁnite squeezing is available. Thus, the output state is no longer the ideal

CV GHZ state – it is rather GHZ-type. Accordingly, total momentum and relative

positions have ﬁnite variances: h[∆( Op

COp

)]

i > 0andh[∆( Ox

Ox

)]

i > 0.

This becomes clear when we express the operators for the output mode i in the

H eisenberg picture [161]:

(0)

r

(0)

r

(0)



r

(0)

r

(0)

r

(0)



(0)



r

(0)



r

(0)

r

(0)



(0)



(0)

. (3.85)

Here, a superscript (0) denotes initial vacuum modes, and r

, r

,andr

are the

squeezing parameters. In addition to the ﬁnite squeezing, the inevitable losses in

the experiment further degrade the entanglement. It is important to stabilize the

relative phase of the three input modes in order to properly adjust the squeezing

directions. The phase ﬂuctuations in this stabilization lead to an extra degradation

of the entanglement. As a result, the output state does not necessarily exhibit gen-

uine tripartite entanglement: it may be fully or partially separable. Therefore, we

need to experimentally verify the full inseparability of the state.

168 3 Entanglement

Afeasibleschemeforthispurposeistocheckthefollowingsetofinequali-

ties [165] (see Section 3.2.1.2):



∆( Ox

Ox

)





∆( Op

COp

C g

)



 1,

II.



∆( Ox

Ox

)





∆(g

COp

)



 1,

III.



∆( Ox

Ox

)





∆( Op

C g

COp

)



 1 . (3.86)

Here, the g

are arbitrary real parameters. Note that the variances of the vacuum

state are h(∆ Ox

(0)

)

iDh(∆ Op

(0)

)

iD1/4.

The violation of inequality I. is a sufﬁcient condition for the inseparability of

modes 1 and 2, and is a criterion for the success of a quantum protocol between

parties 1 and 2. Note that inequality I. alone does not impose any restriction on the

separability of mode 3 from the others. In other words, the success of a quantum

protocol between parties 1 and 2 with the help of party 3 (by conveying classical

information about a measurement of Op

[161]) does not prove the inseparability of

the third party from the rest. Thus, we need to check the violation of at least two

of the three inequalities Eq. (3.86) to verify the ful l inseparability of the tripartite

entangled state.

From Eq. (3.85), we ﬁnd that the optimum gain g

opt

to minimize the l.h.s. of the

inequalities in Eq. (3.86) depends on the squeezing parameters, namely,

opt

C2r

 e

2r

C2r

2r

, (3.87)

where r

D r

(which makes the three-mode state totally symmetric and hence g

opt

independent of i). In the case of inﬁnite squeezing (CV GHZ state), the optimum

gain g

opt

is one, while it is less than one for ﬁnite squeezing. Although the smallest

values of the l.h.s. of the inequalities in Eq. (3.86) are observed when we experi-

mentally adjust g

opt

,Aokiet al. employed g

D 1foralli [188]. This makes the

experimental veriﬁcation simpler. Moreover, the measured variances then directly

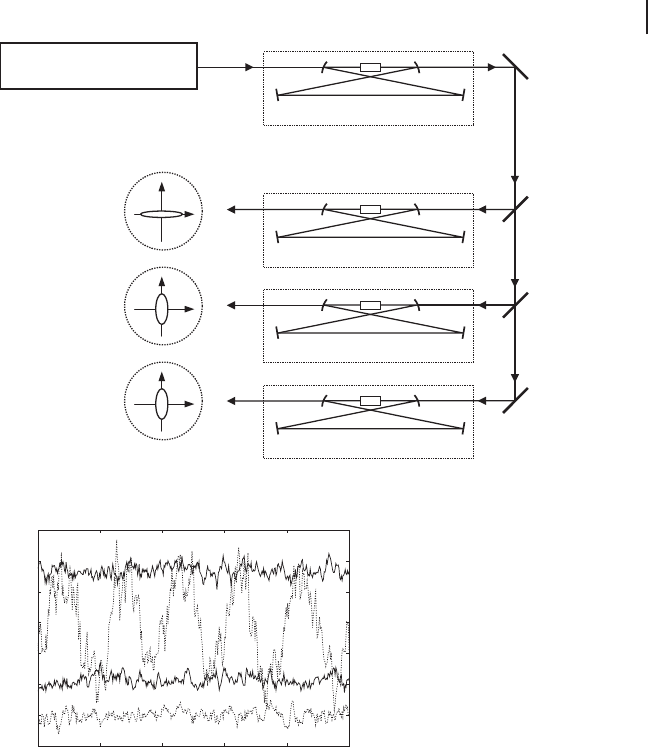
correspond to those of the eigenvalues of the ideal CV GHZ state. Figure 3.23

shows the schematic of the experimental setup to generate three independent

squeezed vacuum states [188].

Figure 3.24 shows the noise-power measurement results on output mode 1 as an

example of noise-power measurements on each output mode. The minimum noise

of 1.14 ˙ 0.25 dB compared to the corresponding vacuum noise level is observed

for the x quadrature, while the maximum noise of 4.69 ˙ 0.26 dB is observed for

the p quadrature. Similarly, the minimum noise of 0.75 ˙ 0.27 and 1.21 ˙ 0.29 dB

for the x quadrature and the maximum noise of 4.12 ˙0.27 and 4.69 ˙0.21 dB for

p are observed for output modes 2 and 3, respectively.

The variances of the relative positions and the total momentum are measured

to check the inequalities in Eq. (3.86). Figure 3.25a shows the schematic of the

3.2 Qumode Entanglement 169

Ti:Sapphire

Doubler

OPO1

OPO3

OPO2

Figure 3.23 Schematic of the generation of three independent squeezed vacuum states [188].

0 0.01 0.02 0.03 0.04 0.05

Time (s)

(i)

(ii)

(iii)

(iv)

-1

Noise Power (dB)

Figure 3.24 Noise measurement results

on output mode 1 alone [188]. (i) repre-

sents the corresponding vacuum noise

h(∆ Ox

(0)

)

iD1/4; (ii) the noise of the x

quadrature h(∆ Ox

)

i; (iii) the noise of the p

quadrature h(∆ Op

)

i; (iv) the noise of the

scanned phase. The measurement frequency

is centered at 900 kHz, resolution bandwidth

is 30 kHz, video bandwidth is 300 Hz. Except

for (iv) traces are averaged ten times.

measurement of the variances h[∆( Ox

Ox

)]

i and h[∆( Ox

Ox

)]

i.Theoutputs

of the homodyne detection are electronically subtracted, and the noise power is

measured by spectrum analyzers. The variance h[∆( Ox

Ox

)]

i is measured in a

similar manner. In the case of the variance h[∆( Op

COp

)]

i,thenoisepower

of the electronical sum of the homodyne detection outputs is measured as shown

in Figure 3.25b.