Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing

Подождите немного. Документ загружается.

240 5 Quantum Error Correction

e + f

e – f

Alice

Bob

State preparation

State verification

Distillation

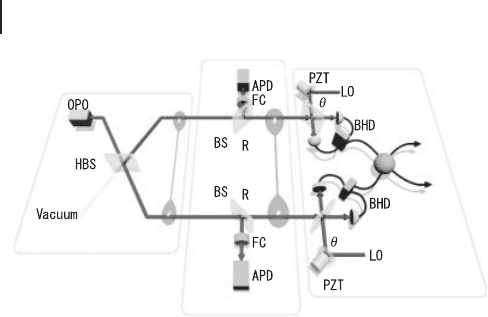
Figure 5.15 Experimental setup for for CV

entanglement distillation demonstrated by

Taka hash i et al. [264]. OPO: optical parametric

oscillator for creation of squeezed vacuum,

HBS: half beam splitter, BS: beam splitter, R:

Reﬂectivity of beam splitter, BHD: balanced

homodyne detector, LO: local oscillator, θ:

local oscillator phase, FC: ﬁltering cavity, APD:

avalanche photodiode, PZT: piezo electric

transducer.

sion on the necessary paradigm shift from frequency to time in Section 3.2.3. The

DV-type photon-subtraction-based distillation of CV entanglement represents an

important example of a protocol whose realization relies upon such a new genera-

tion of experiments. According to our deﬁnition, it is an example of a hybrid pro-

tocol, ex ploiting at the same time unconditionally producible, Gaussian resource

states and DV measurements. In this sense, the experiment described below could

as well be listed among those hybrid schemes that we shall discuss in Chapter 8.

Figure 5.15 shows the experimental setup for CV entanglement distillation

demonstrated by Takahashi et al. [264]. The scheme itself was proposed by Opatrný

for improvement of CV teleportation ﬁdelities [261]. In this scheme, two-mode

EPR-like state created by two squeezed vacua and a beam splitter is distilled

by using “photon subtraction” technique which is also used for creation of a

“Schrödinger kitten” and will be explained in more detail in Section 8.2.

In Figure 5.15, ﬁrst, two entangled light beams are created with a squeezed vac-

uum and a half beam splitter. Then, a single photon is subtracted from one of

the beams, or singl e photons are subtracted from both beams with avalanche pho-

todiodes (APDs). More precisely, the outputs of the balanced homodyne detectors

(BHDs) are recorded by a digital oscilloscope triggered by either logical OR or AND

of the click signals from the two APDs. Here, ﬁltering cavities (FCs) before the

APDs correspond to frequency-mode ﬁlters which only select the same frequency-

mode as local oscillators (LOs) for BHDs. For the state veriﬁcation, a set of the

homodyne outcomes are numerically converted into the “C/” basis which corre-

spond to two outputs from a virtual half beam splitter. If the experiment succeeds,

the outputs from the virtual half beam splitter should be an “odd” Schrödinger kit-

ten (jαijαi, jαj1) and a vacuum for single photon subtraction from one

of the beams or OR case of the click signals from APDs, and should be an “even”

Schrödinger kitten (jαiCjαi, jαj1) and a vacuum for single photon subtrac-

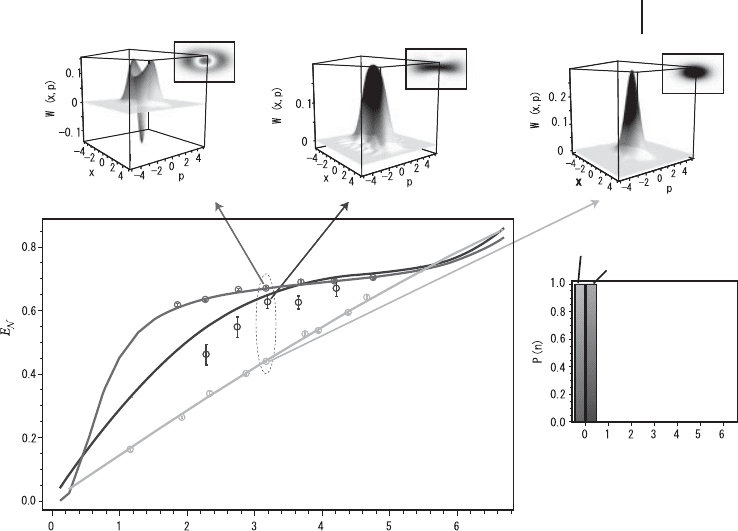
5.5 Experiment: Entanglement Distillation 241

(a)

(d)

(b) (c)

(e)

Initial squeezing (dB)

Photon number

Undistilled

Two-photon

Single-photon

Two-photon

Single-photon

Log negativity,

Figure 5.16 Experimental results for for

CV entanglement distillation demonstrat-

ed by Takahashi et al. [264]. Experimentally

reconstructed Wigner functions and con-

tour plots of the “” mode states for the

distilled state via single photon subtraction

with R D 5% (a), distilled state via two-

photon subtraction with R D 10% (b), and

the undistilled initial state (squeezed vacuum

with R D 0%) (c), all with initial squeez-

ing of 3.2 dB. (d) Experimental logarithmic

negativities as functions of the initial squeez-

ing. Single-photon: single-photon subtracted

states, Two-photon: two-photon subtracted

state. (e) Photon number distributions of

the experimentally reconstructed “C”mode

states corresponding to (a) and (b).

tion from both beams or AND case of the click signals from APDs. Here, the “odd”

Schrödinger kitten will be explained in Section 8.2 and the “even” Schrödinger kit-

ten is just the extension of single photon subtraction for “odd” kitten creation to

two photon subtraction [267].

Figure 5.16 shows the experimental results for the CV entanglement distillation

demonstrated by Takahashi et al. [264]. From Figure 5.16, we can see the Wigner

function of an “odd” Schrödinger kitten for single photon subtraction and the one

of an “even” Schrödinger kitten for single photon subtraction from both beams

or two photon subtraction. It is clear from the results that the distillation is suc-

cessfully performed for both single photon subtraction from one of the beams and

single photon subtractions from both beams. Moreover, the values of the logarith-

mic negativity show that the entanglement increases through distillation.

Part Three Measurement-Based and Hybrid Approaches

245

Quantum Teleportation of Gates

In Section 1.6, we introduced quantum teleportation as a protocol to reliably trans-

fer arbitrary, “unknown” quantum states using shared entanglement and classical

communication. In the ideal case, an unknown qubit state can be perfectly restored

at the receiving station while the ideal scenario for a perfect transfer of an inﬁnite-

dimensional qumode state is unphysical and corresponds to the limiting case of

quantum teleportation using two-mode squeezed states (see Section 3.2) with in-

ﬁnite squeezing and energy. Real experiments in which optical qubit or qumode

states were teleported using physical resources, such as polarization-entangled

photon pairs or ﬁnitely squeezed two-mode squeezed states, were discussed in

Chapter 4.

In this chapter, we shall now explain various experiments in which the true

power of quantum teleportation was revealed, namely, as a primitive for quan-

tum information processing and computing. The initial quantum states in such

teleportation-based approaches are to be manipulated and processed through tele-

portation, and not simply transferred from a sender to a receiver – entanglement-

assisted communication becomes entanglement-assisted computation. This gener-

alization of quantum teleportation may be referred to as gate teleportation extend-

ing the original notion of state teleportation.

This gate teleportation [84] is the simplest manifestation of measurement-based

quantum information processing: as opposed to standard quantum teleportation,

a suitably modiﬁed entangled-state resource is employed with the corresponding

gate applied upon that resource state ofﬂine prior to the actual computation. The

computation itsel f is then conducted in the same manner as in state teleportation

by performing a Bell measurement jointly on the input state for the desired gate and

one half of the entangled resource state. This joint measurement contains an en-

tangling element as it projects onto an entangled-state basis. For a different gate,

the entangled resource state has an accordingly different gate applied on it and

hence must vary depending on the algorithm to be computed. In contrast, in an

ultimate manifestation of measurement-based quantum information processing,

the ofﬂine resource state would always remain ﬁxed during the entire computation

and the measurements on it would be local single-party projections whose orthog-

onal measurement bases can be adjusted depending on the individual gates of the

algorithm to be computed. All entangling gates would be performed ofﬂine in this

Quantum Teleportation and Entanglement. Akira Furusawa, Peter van Loock

ISBN: 978-3-527-40930-3

246 6 Quantum Teleportation of Gates

case. This so-called cluster-state computation (recall also Section 1.8) and the cor-

responding experiments will be discussed in Chapter 7.

It turned out that the ofﬂine-resource-based and measurement-based approaches

offer a distinct advantage over those schemes with every single gate performed di-

rectly and unitarily online: the ofﬂine gates may be implemented in a probabilistic

fashion until they succeed; only for these successful events are the ofﬂine states de-

livered for consumption during the online computation. This feature is particularly

useful for DV qubit processing with single photons where entangling gates (or the

essential elements of it) cannot be achieved with near-unit, but with a reasonable,

nonzero success probability. In this approach, the measurement itself is used to in-

duce the required nonlinearity to achieve the universal gate (see Section 1.8). The

seminal theoretical work by Knill, Laﬂamme, and Milburn (“KLM”) [242], which

initiated linear-optics measurement-based quantum information processing, and

experiments related with this proposal will be discussed in Sections 6.1.1 and 6.1.2,

respectively.

In the CV qumode case, experimentally inefﬁcient interactions such as non-

Gaussian operations can be implemented ofﬂine. Moreover, even Gaussian squeez-

ing gates, otherwise hard to apply upon arbitrary quantum optical states, that is,

states other than the vacuum, can be enacted in an ofﬂine fashion. Experiments

along these lines will be described in Section 6.2.1, including a universal squeez-

er (Section 6.2.1.1) and a Quantum Non-Demolition (QND) gate (Section 6.2.1.2).

Finally, in Section 6.2.2, we brieﬂy discuss alternate protocols for realizing univer-

sal quantum gates including a kind of CV version of KLM, namely, the CV gate

teleporter by Bartlett and Munro [268].

6.1

Teleporting Qubit Gates

6.1.1

KLM

In Section 2.8, we explained that, besides a direct implementation of universal

gates through nonlinear optical interactions (which are hard to obtain efﬁcient-

ly), one may use the so-called multiple-rail encoding for which arbitrary quantum

gates are realizable through linear optics alone [134]. However, this very ﬁrst linear-

optics quantum computer proposal is not scalable. A breakthrough towards an in-

principle efﬁcient, scalable quantum computer based upon linear optics came with

the KLM proposal [242].

The KLM scheme is a fully DV-based protocol, demonstrating that, in princi-

ple, passive linear optics and DV photonic auxiliary states are sufﬁcient for (the-

oretically) efﬁcient, universal DV quantum computation. Inducing nonlinearity

through photon counting measurements renders the KLM scheme nondetermin-

istic. However, the probabilistic quantum gates can be made asymptotically near-

deterministic by adding to the toolbox feedforward and complicated, multi-photon

6.1 Teleporting Qubit Gates 247

NSS

CSIGN

BSBS

NSS

CSIGNCSIGN

Figure 6.1 Implementing a probabilistic controlled sign gate (CSIGN  C

)ontwosingle-rail

qubits using two nondeterministic NSS gates. The resulting two-qubit gate works in a similar

way to the deterministic implementation described in Figure 2.15 using Kerr nonlinearities.

entangled auxiliary states with sufﬁciently high photon numbers, and by employ-

ing quantum teleportation [84]. KLM is “in-principle efﬁcient”, as the number of

the ancillary photons grows only polynomially with the success rate. Fidelities are

always, in principle, perfect in the KLM approach.

The essential ingredient for the nondeterministic realization of a two-photon

two-qubit entangling gate (in dual-rail encoding) is the one-mode nonlinear sign

shift (NSS) gate. It acts on the qutrit subspace fj0i, j1i, j2ig of the optical Fock space

as jki!(1)

k(k1)/2

jki. Placing two such NSS gates in the middle between two

beam splitters will then act as a controlled sign gate, jki˝jli!(1)

jki˝jli,

on two single-rail as well as two dual-rail qubits. In fact, we may replace the de-

terministic Kerr-based circuit of Figure 2.15 by the equivalent circuit depicted in

Figure 6.1. The latter, however, becomes nondeterministic with NSS gates operat-

ing only probabilistically.

In the original KLM proposal, the NSS gate can be realized with 1/4 success

probability, corresponding to a success probability of 1/16 for the full controlled

sign gate as shown in Figure 6.1. In subsequent works, this efﬁciency was slightly

improved [269]. There are also various, more general treatments of these nondeter-

ministic linear-optics gates deriving bounds on their efﬁciencies [270–272].

Probabilistic quantum gates cannot be used directly for quantum computation.

The essence of KLM (see Figure 6.2) is that near-unit success probabilities are at-

tainable by combining nondeterministic gates on ofﬂine entangled states with the

concept of quantum gate teleportation [84]. As the necessary Bell measurements

for quantum teleportation succeed at most with 1/2 probability, if onl y ﬁxed arrays

βα+

U(k)

βα+

U(k)

βα+

Figure 6.2 Making nondeterministic gates

near-deterministic through single-rail quan-

tum teleportation. The Bell measurement is

performed by means of the linear-optics cir-

cuit U plus photon counting. For an entangled

two-mode state jΦ i/j10iCj01i with one

ancilla photon, teleportation only succeeds in

one half of the cases. For larger ancillae with

sufﬁciently many photons, teleportation can

be made almost perfect. In order to teleport

a gate near-deterministically onto an input

state, the corresponding gate must be ﬁrst

applied ofﬂine and probabilistically to the

multi-photon entangled ancilla state.

248 6 Quantum Teleportation of Gates

of beam splitters are used [196], entangled ancilla states and feedforward must be

added to boost efﬁciencies beyond 1/2 to near 1.

To sum up, the efﬁciency of KLM comes from mainly two facts: (1) they use

dual-rail encoding (instead of multiple-rail encoding which scales exponentially)

using only one photon per qubit; (2) they achieve near-unit gate efﬁciencies (near-

deterministic gate operations) with auxili ary photons scaling only polynomial ly

with any desired efﬁciency.

Even though KLM is “in-principle efﬁcient”, it is still highly impractical as near-

deterministic operations would require ancilla states too complicated to engineer

with current experimental capabilities. It is therefore extremely important to fur-

ther enhance the efﬁciencies of linear-optics quantum computation with regard to

the resource scaling. Steps into this direction have been made already by merging

the teleportation-based KLM approach with the fairly recent concept of one-way

(cluster) computation [1] (see Chapter 7).

6.1.2

Experiment: Qubit Gates

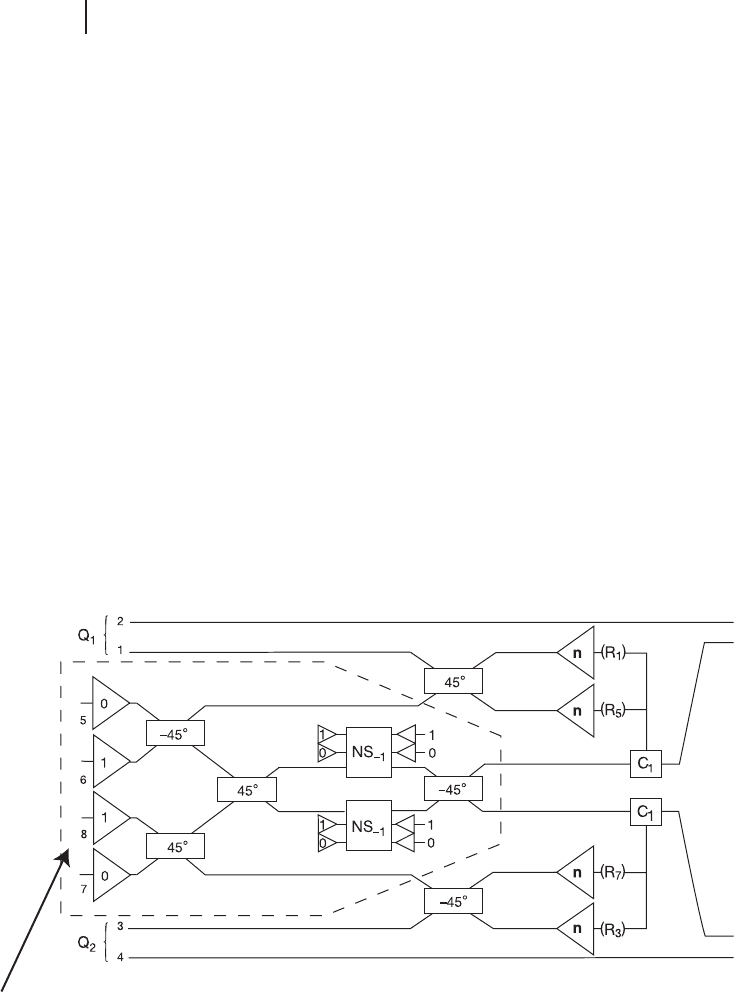
As shown in the previous section and in Figure 6.3, the essence of the KLM scheme

is that the CPhase gate is reduced to state preparation and teleportation. Although

there is no report of full implementation of the KLM scheme at the moment,

there is some reports for conditional CPhase or CNOT gate for the state prepa-

State preparation

Teleportation

Figure 6.3 Conditional CPhase gate with success probability 1/4 proposed by Knill et al. [242].

The essence of this protocol is that the CPhase gate is reduced t o state preparation and telepor-

tation.

6.1 Teleporting Qubit Gates 249

Figure 6.4 A schematic of the CNOT gate re-

alized by O’Brien et al. [273]. The theoretical

success probability is 1/9. (a) A conceptual

description of the gate. (b) A polarization en-

coded photonic qubit can be converted into

a spatially encoded qubit suitable for the gate

shownin(a)usingapolarizationbeamsplit-

ter (PBS) and a half wave plate (HWP) set to

rotate the polarization of one of the outputs

by 90

. The reverse process converts the spa-

tial encoding back to polarization encoding.

gate.

ration [273]. In this section, we will explain the experiment performed by O’Brien

et al. [273]indetailasatypicalexample.

Figure 6.4 shows a schematic of conditional CNOT gate with linear optics

and post-selection demonstrated by O’Brien et al. [273]. This conditional CNOT

gate can be used for the state preparation for the KLM scheme as mentioned

above.

The main trick is shown in Figure 6.4a. This trick was proposed by Ralph

et al. [274], which is illustrated in Figure 6.5. We ﬁrst use the Heisenberg picture

and will derivate the operator input–output relation of the beam splitter network

showninFigure6.5.

A beam splitter input–output relation is (see Chapter 2)

1out

η Oa

1in

1  η Oa

2in

2out

1  η Oa

1in



η Oa

2in

, (6.1)

where η is the reﬂectivity of the beam splitter. By using this beam-splitter relation,

we can get the input–output relation of the beam splitter network in Figure 6.5 as