Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing
Подождите немного. Документ загружается.

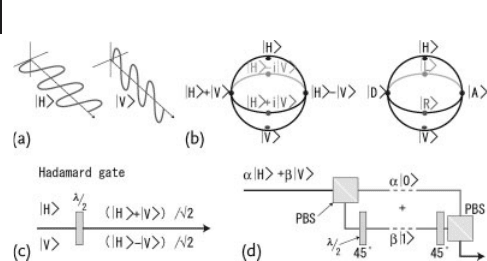
100 2 Introduction to Optical Quantum Information Processing
Figure 2.8 Representing and manipulating a
polarization qubit encoded in a single photon
wavepacket [115]. (a) H and V denote hori-
zontal and vertical polarization, respectively.
(b) An arbitrary qubit state can be represented
on the Bloch sphere (known as the Poincaré
sphere in optics). Examples of diagonal (D),
anti-diagonal (A), right circular (R), and left
circular (L) polarization states are shown.
(c) A half-waveplate (λ/2) can be used to
perform a Hadamard transformation. (d) A
polarization qubit can be converted into a
spatial (path-encoded) qubit by means of a
polarization beam splitter (PBS).
encoded) qubit αj0, 1iCβj1, 0i (jupper photon number, lower photon numberi)
through a polarization beam splitter (PBS) (Figure 2.8d).
Typically, in the language of quantum information, H and V are chosen as the
computational basis, corresponding to the ˙1 eigenstates of the Pauli Z operator.
In this case, the other two bases on the equatorial circle which are superposition
states of H and V correspond to the ˙1 eigenstates of the Pauli X and Y opera-
tors. These are the one-qubit stabilizer states ( Section 1.2) in polarization encod-
ing.
2.2.8
Photonic Qumodes
Apart from discrete photon numbers, an optical state may be described by its am-
plitude and phase. The corresponding quantum phase-space variables could be
considered the quantum analogues of classical, analog encoding. Such qumode
encoding, that is, CV quantum information encoded into optical modes, leads to
states which are rather sensitive to noise, but can be processed in an unconditional
fashion; even entangling gates can be accomplished through deterministic, linear
optics (see Chapter 3).
In the linear, CV Gaussian regime, the optical encoding into qumodes is achieved
either through approximate x/p-eigenstates (l argely squeezed states), for which
projection measurements are well approximated by homodyne detections (see Sec-
tion 2.6); alternatively, the overcomplete and non-orthogonal set of coherent states
may serve as a basis for qumodes. Perfectly projecting onto this basis is only possi-
ble for sufficiently large amplitudes jαj, for which the coherent states become near-
orthogonal. Nonetheless, two coherent states can also be unambiguously discrimi-
nated in the regime of small amplitudes using a beam splitter, an ancilla coherent

2.2 Quantum Optical States and Encodings 101
α=A
α±
α2
α2−
0
0
""+
""−
α=A
α±
α2
α2−
0
0
""+
""−
=
±
−
+
−
Figure 2.9 Optimal unambiguous state discrimination of
equally occurring, binary coherent states fj˙αig using a beam
splitter, an ancilla coherent state, and on/off detectors. The
inconclusive event here corresponds to the detection of the
two-mode vacuum e
α
2
j00i for the two output modes with
probability e
2α
2
(α 2 R). Another discussion related with this
measurement is presented in Section 2.5.2.
state, and on/off detectors (see Figure 2.9 and Section 2.5.2). This unambiguous
state discrimination (USD) is probabilistic, but, in principle, error free.
In the following two sections, we shall start establishing a connection between
properly normalized qumode stabilizer states, that is, the physical CV analogues of
the DV stabilizer states, and CV Gaussian pure states.
2.2.8.1 Stabilizer States
Consider a single qumode. In Section 1.2, we found that the stabilizers
7)
in
Eq. (1.50) represent an infinite set of rotated quadrature eigenstates obtained
by phase-rotating an unphysical momentum eigenstate,
O
R(θ )jpi.Now,wewishto
generalize the CV qumode stabilizer states to properly normalized, physical states.
It will turn out that the G aussian pure states play this role, and hence for a sin-
gle qumode, the stabilizer must uniquely represent a displaced squeezed vacuum
state, jα, ζ iD
O
D(α)
O
S(ζ)j0i.
8)
Let us start by introducing the stabilizer operator of the vacuum state of a single
qumode with mode operator Oa.Weobtain
exp(α Oa)j0iDexp[α( Ox C i Op)]j0iDj0i . (2.80)
Note that, although the mode operator Oa is non-Hermitian and exp(α Oa)non-
unitary, the exponentiated Oa operator does behave like a stabilizer, uniquely rep-
resenting the vacuum state as the only eigenstate with +1 eigenvalue. From this,
we get the stabilizer for a single-mode squeezed vacuum state, with squeezing
parameter r > 0foranx-squeezing operation
O
S(r) D exp[ir( Ox Op COp Ox)], through
inverse Heisenberg evolution,
O
S(r)exp[α( Ox C i Op)]
O
S
†
(r) D exp
h
α(e
Cr
Ox C ie
r
Op)
i
. (2.81)
In the case of momentum squeezing, with
O
S(r), we have
O
S(r)exp[α( Ox Ci Op )]
O
S
†
(r) D exp
h
α(e
r
Ox Cie
Cr
Op)
i
. (2.82)
Let us rewrite this as
9)
exp
α
2
/4
X(αe
Cr
/2)Z[αe
r
/(2i)]. (2.83)
7) For a definition and a discussion of stabilizers, see Section 1.9.
8) The standard formalism to describe Gaussian states will be introduced in the following section.
9) All of these expressions are convention-dependent; recall that our convention is „D1/2.

102 2 Introduction to Optical Quantum Information Processing
Now , we define α 2e
r
s such that the momentum-squeezed stabilizer be-
comes
exp
e
2r
s
2
X(s)Z
ie
2r
s
. (2.84)
In the limit of infinite p-squeezing r !1, this operator approaches X(s), which
stabilizes the zero-eigenstate jp D 0i, X(s)jp D 0iDjp D 0i, 8s 2 R,asexpected.
In order to represent not only squeezed states like
O
S(r)j0i, but also the rotated
states
O
S(ζ )j0i, we use the rotated momentum-squeezed-vacuum stabilizer,
e
e
2r
s
2
O
R(θ )X(s)
O
R
†
(θ )
O
R(θ )Z
ie
2r
s
O
R
†
(θ )
D e
e
2r
s
2
(1ie
2r
cos θ sin θ )
g
(θ )
p D0
(s)Z
ie
2r
s cos θ
X
ie
2r
s sin θ
g
(θ )
p D0
(s, r) , (2.85)
which becomes the rotated-zero-momentum stabilizer in the limit r !1,with
g
(θ )
p
(s) from Eq. (1.50) and Eq. (1.71). Finally, we only have to express a complex
phase-space displacement affected by
O
D(α) through stabilizers (which we implicit-
ly did already for defining the unphysical qumode stabilizer x and p eigenstates in
Section 1.2). While the stabilizer for a displaced vacuum state,
O
D(α)j0i,issimply
O
D(α)e
s
2
X(s)Z(is)
O
D
†
(α) D e
s
2
e
2sα
X(s)Z(is) , (2.86)
using Eq. (2.84) with r D 0, we obtain the following general stabilizer for a single-
qumode Gaussian pure state,
O
D(α)g
(θ )
p D0
(s, r)
O
D
†
(α)
D e
C2s cos θ
(
e
2r
x
α
Cip
α
)
2is sin θ
(
x
α
Cie
2r
p
α
)
g
(θ )
p D0
(s, r) , (2.87)
using Eq. (2.85). This is the stabilizer for an arbitrary displaced squeezed vacuum
state,
O
D(α)
O
S(ζ)j0i, depending on four real parameters, x
α
, p
α
, r,andθ ,withα D
x
α
C ip
α
. In Section 3.2, we shall utilize stabilizers for Gaussian multi-mode pure
states in order to define and represent multipartite entangled qumode cluster and
graph states.
2.2.8.2 Gaussian States
Consider the Wigner function of a displaced position-squeezed vacuum state for a
single qumode in Eq. (2.59). It may be rewritten in the following way,
W(x, p ) D
2
π
exp
1
2
(
x x
α
, p p
α
)
4e
C2r
0
04e
2r
x x
α
p p
α
,
(2.88)
or, using a more compact notation,
W(ξ ) D
1
(2π)
N
p
det V
(N)
exp
1
2
(ξ ξ
0
)
V
(N)
1
(ξ ξ
0
)
T
, (2.89)

2.2 Quantum Optical States and Encodings 103
with N D 1, the 2-dimensional vectors ξ D (x, p ), ξ
0
D (x
α
, p
α
), and the 2 2
matrix
V
(1)
D
1
4
e
2r
0
0e
C2r
. (2.90)
This matrix contains the (co-)variances of the displaced position-squeezed vacuum
state, namely, h(∆ Ox)
2
iDhOx
2
ix
2
α
D e
2r
/4, h(∆ Op)
2
iDhOp
2
ip
2
α
D e
C2r
/4,
using Eq. (1.40), and h( Ox Op COp Ox)i/2 x
α
p
α
D 0.
More generally, Eq. (2.89) for N D 1, with a real, symmetric 2 2covariance
matrix V
(1)
, represents an arbitrary displaced squeezed thermal state and therefore
an arbitrary single-qumode Gaussian state. Such a state is determined through
five parameters; three for the displaced position-squeezed state, x
α
, p
α
,andr;an
extra phase rotation θ and a thermal excitation number (see below). Compared to
the stabilizer states presented in the preceding section, here, a general Gaussian
state for a single qumode can be pure or mixed.
10)
The Wigner function for a
general multi-mode Gaussian state is also expressed by Eq. (2.89), in this general
case with a 2N -dimensional vector ξ having the quadrature pairs of all N modes as
its components,
ξ D (x
1
, p
1
, x
2
, p
2
,...,x
N
, p
N
),
O
ξ D ( Ox
1
, Op
1
, Ox
2
, Op
2
,..., Ox
N
, Op
N
) , (2.91)
and similarly for the first moments, ξ
0
D (hOx
1
i, hOp
1
i, hOx
2
i, hOp
2
i,...,hOx
N
i, hOp
N
i). In
general, the covariance matrix is then given by V
(N)
ij
Dh(
O
ξ
i
O
ξ
j
C
O
ξ
j
O
ξ
i
)/2ih
O
ξ
i
ih
O
ξ
j
i.
However, many important properties in the multi-mode case, such as entangle-
ment, are independent of the first moments, as these can always be locally adjusted
through phase-space displacements. We may therefore assume zero first moments
and define the 2N 2N correlation matrix V
(N)
, having as its elements the second
moments symmetrized according to the Weyl correspondence in E q. (2.71),
Tr
h
O
∆
O
ξ
i
∆
O
ξ
j
C ∆
O
ξ
j
∆
O
ξ
i
/2
i
D
D
O
ξ
i
O
ξ
j
C
O
ξ
j
O
ξ
i
/2
E
D
Z
W(ξ )ξ
i
ξ
j
d
2N
ξ V
(N)
ij
, (2.92)
where ∆
O
ξ
i
D
O
ξ
i
h
O
ξ
i
iD
O
ξ
i
for zero first moments. F or (zero-mean) Gaussian
states of the form in Eq. (2.89), the Wigner function is completely determined
by the second-moment correlation matrix. In order to represent a physical state
(Gaussian or non-Gaussian), the correlation matrix must be real, symmetric, and
positive; in addition, it must be consistent with the commutation relation from
Eq. (1.39) [116, 117],
[
O
ξ
k
,
O
ξ
l
] D
i
2
Λ
kl
, k, l D 1,2,3,...,2N . (2.93)
10) As discussed in Section 1.9, stabilizer states can be generalized in terms of stabilizer codes, which
gives an interesting recipe for extending the qumode stabilizer formalism from Gaussian pure to
Gaussian mixed states.
104 2 Introduction to Optical Quantum Information Processing
Here, the 2N 2N “symplectic matrix” Λ is block diagonal and contains the 2 2
matrix J as the diagonal entries for each quadrature pair,
Λ D
N
M
kD1
J , J D
01
10
. (2.94)
A direct consequence of this commutation relation and the non-negativity of the
density operator O is then the following N-mode uncertainty relation,
V
(N)
C
i
4
Λ 0 . (2.95)
This matrix equation means that the matrix sum on the left-hand side only has non-
negative eigenvalues. The N-mode uncertainty relation is a necessary condition on
any physical state. For Gaussian states, however, it is also a sufficient condition that
guarantees the positivity of O [117]. In the simplest case of a single qumode, N D 1,
Eq. (2.95) is reduced to the statement hOx
2
ih Op
2
i1/4hOx Op COp Oxi
2
D det V
(1)
1/16,
which is a stronger version of the Heisenberg uncertainty relation in Eq. (1.43).
11)
For any N, (2.95) becomes exactly the Heisenberg uncertainty relation of Eq. (1.43)
for each individual mode, if V
(N)
is diagonal.
Gaussian states
one qumode: pure state is displaced squeezed vacuum state:
O
D(α)
O
S(ζ)j0i (2 parameters α, ζ 2 C 4 parameters x
α
, p
α
, r, θ 2 R)
pure state is stabilized by e
C2s cos θ (e
2r
x
α
Cip
α
)2i s sin θ (x
α
Cie
2r
p
α
)
g
(θ )
p D0
(s, r)
mixed state is displaced squeezed thermal state:
1
1 CNn
O
D(α)
O
S(ζ)
Nn
1 CNn
Oa
†
Oa
O
S
†
(ζ )
O
D
†
(α) (5 parameters x
α
, p
α
, r, θ , Nn)
Nqumodes: zero-mean Gaussian-state Wigner function:
W(ξ ) D
1
(2π)
N
p
det V
(N)
exp
1
2
ξ
V
(N)
1
ξ
T
real, symmetric, positive correlation matrix:
V
(N)
ij
D
D
O
ξ
i
O
ξ
j
C
O
ξ
j
O
ξ
i
ı
2
E
D
Z
W(ξ )ξ
i
ξ
j
d
2N
ξ , V
(N)
C
i
4
Λ 0
Λ D
N
M
kD1
J , J D
01
10
,
h
O
ξ
k
,
O
ξ
l
i
D
i
2
Λ
kl
, k, l D 1,2,3,...,2N
11) That is, det V
(1)
1/16 implies hOx
2
ih Op
2
i1/16, but the converse is not generally true.

2.2 Quantum Optical States and Encodings 105
N real, positive, symplectic eigenvalues:
ˇ
ˇ
eigenvalues of iΛV
(N)
ˇ
ˇ
uncertainty relation:
ν
k
1
4
, 8k D 1,2,...,N , V
(N)
C
i
4
Λ 0
pure states:
ν
k
D
1
4
, 8k D 1,2,...,N
mixed states:
9k 2f1,2,...,Ng such that ν
k
>
1
4
We should also mention here that there is an equivalent representation of the
uncertainty relation in Eq. (2.95) using the so-called symplectic eigenvalues.There
are N real, positive, symplectic eigenvalues and these are obtained for any N-mode
Gaussian state through Williamson diagonalization [118] of its correlation matrix
into normal modes,
V
(N)
D S
T
N
V
(N)
S , (2.96)
where the matrix S 2 Sp(2N, R) describes a global symplectic transformation.
12)
The resulting diagonal matrix
N
V
(N)
contains the N symplectic eigenvalues ν
k
,
N
V
(N)
D
N
M
kD1
ν
k
0
0 ν
k
. (2.97)
The uncertainty relation in Eq. (2.95) can then be recast as (S
1
)
T
V
(N)
S
1
C
i/4( S
1
)
T
ΛS
1
D
N
V
(N)
C i/4Λ 0, which corresponds to
ν
k
1
4
, 8k D 1,2,...,N . (2.98)
The effect of the Williamson diagonalization is that any correlations between the
quadratures and between the modes are eliminated such that the resulting corre-
lation matrix represents an N-mode product state with every qumode in a thermal
state,
N
V
(N)
D
N
M
kD1
V
(1)
k
, V
(1)
k
D
1
4
1 C 2 Nn
k
0
01C 2 Nn
k
. (2.99)
12) The linear, symplectic transformations S on the 2N-dimensional phase space form the symplectic
group Sp(2N, R), where S
T
ΛS D Λ and hence det S D 1, 8S 2 Sp(2N, R). The symplectic
transformations correspond to the Gaussian unitaries up to displacements (see Section 2.4).

106 2 Introduction to Optical Quantum Information Processing
The parameters Nn
k
D (4ν
k
1)/2 are the mean thermal excitation numbers for
every one of the N qumodes after diagonalization. The corresponding density op-
erator is a tensor product state of thermal states for qumode k,
13)
O
k
D
2
4ν
k
C 1
1
X
nD0
4ν
k
1
4ν
k
C 1
n
jnihnjD
1
1 CNn
k
1
X
nD0
Nn
k
1 CNn
k
n
jnihnj.
(2.100)
As a result, the symplectic eigenvalues contain the entire information about the
physicality, purity, and mixedness of the N-mode Gaussian state. Any physical state
must satisfy Eq. (2.98). The structure and the size of the thermal noise that makes
the state a mixed state is determined by the number of symplectic eigenvalues with
ν
k
> 1/4 and by the extent to which the minimum-uncertainty vacuum bound
ν
k
D 1/4 is exceeded, respectively.
14)
C ompared to the position-squeezed vacuum state in Eq. (2.90), the position-
squeezed thermal state for a single qumode has the following correlation matrix,
V
(1)
D
1
4
e
2r
(1 C 2 Nn)0
0e
C2r
(1 C 2 Nn)
. (2.101)
Compared with the mean photon number as given in Eq. (2.60), we obtain for the
displaced squeezed thermal state,
hOniDhOx
2
iChOp
2
i
1
2
Djαj
2
C sinh
2
r CNn cosh 2r , (2.102)
using Eq. (2.37). This is the mean photon number for an arbitrary single-qumode
G aussian state. It depends on three parameters: the size of the coherent amplitude
jαj, the amount of squeezing r, and the mean thermal number Nn. This photon
number is independent of the phases in α and ζ for a general displaced squeezed
thermal state. Further, the purity for an N-mode Gaussian state depends on
15)
Tr O
2
D
1/4
N
p
det V
(N)
D
1/4
N
Q
N
kD1
ν
k
, (2.103)
13) Where the mean excitation numbers can be
associated with a temperature according to
Nn D 1/(e
β
1) with the usual parameter
β D
„ω
k
B
T
.Notethat,whiletheuncertainty
relation bound and the symplectic
eigenvalues are convention-dependent (in
our case with „D1/2), the mean thermal
number, of course, is not.
14) One may define the number of symplectic
eigenvalues different from 1/4, i.e., the
number of non-vacuum normal modes as
the symplectic rank [119], in analogy to the
standard rank R of a finite-dimensional
density operator corresponding to the
number of its nonzero eigenvalues.
For example, a d-dimensional state has
R D 1whenitispureandR D d
when it corresponds to an incoherent
mixture with d terms. However, a full rank
R D d-state, though having a complex
noise structure, may still have low noise
with most eigenvalues almost vanishing.
In the Gaussian case, a pure state has zero
symplectic rank, whereas a mixed state
has a noise structure given by a symplectic
rank between one and N,andasizeofthe
noises given by the respective values of the
symplectic eigenvalues between 1/4 and
infinity.
15) Which can be derived using Tr O
2
D
π
N
R
d
2N
ξ W
2
(ξ) for Gaussian Wigner
functions W(ξ ) from Eq. (2.89).

2.2 Quantum Optical States and Encodings 107
according to Eq. (1.21). A pure state has det V
(N)
D 1/16
N
,forinstance,detV
(1)
D
1/16 for one qumode, which is the minimal bound of the one-mode uncertainty
relation, as mentioned before.
Finally, let us mention that there is an easy way to compute the symplectic eigen-
values directly from the correlation matrix. First, one has to calculate the ordinary
eigenvalues of the Hermitian matrix iΛV
(N)
.Themodulusofeachoftheresulting
2N real eigenvalues then gives the N real and positive values ν
k
, k D 1,2,...,N.
In this section, we defined multi-mode Gaussian states using Wigner functions
and correlation matrices. A general Gaussian state of a single qumode is a displaced
squeezed thermal state; a Gaussian pure state of a single qumode is a displaced
squeezed vacuum state as well as a physical, properly normalized qumode stabiliz-
er state. Physical stabilizer states for many qumodes, corresponding to (entangled)
multi-mode Gaussian pure states, will be discussed in Section 3.2.
2.2.9
Experiment: Broadband Qumodes
In quantum optical CV experiments, we have to define the qumodes as some physi-
cal modes of light, for example, temporal, frequency, spatial, or polarization modes.
In any case, they will represent wavepackets of the electromagnetic field with vari-
ous time duration. One extreme is infinite time duration as shown in Figure 2.10a –
a continuous wave or a frequency single mode. Usually, a frequency single mode is
realized as a sideband of the fundamental carrier light. In this case, each sideband
corresponds to a qumode. Two sidebands i, j have no overlap in frequency domain
and satisfy the commutators [ Oa
i
, Oa
†
j
] D δ
ij
and [ Oa
i
, Oa
j
] D 0. Another extreme is
very short time duration as shown in Figure 2.10b – pulsed light. In this case, each
pulse corresponds to a qumode. Two pulses i, j do not have any overlap and would
then also satisfy the commutators [ Oa
i
, Oa
†
j
] D δ
ij
and [ Oa
i
, Oa
j
] D 0.
However, the mode operators for pulsed light represent temporal modes at times
t
i
of which each mode contains a finite bandwidth of frequency modes, Oa
t
i
D
R
dωg(ω) Oa
ω
, with some spectral function g(ω)thatisalmostflatinthislimit.The
other limit of a frequency single mode is then approached for g(ω) ! δ(ω
i
). In
the experiment, the realistic situation will be between these two extremes.
As mentioned above, a frequency sideband of a carrier light beam is often used
for a frequency single mode. The bandwidth ∆ f is usually very narrow compared
to the sideband frequency f (∆ f f ). So the wavepacket of the qumode has
time duration of 1/∆ f which is extremely long, and thus the spatial size of the
wavepacket is very long (c/∆ f , c: speed of light). From this point of view, the
wavepacket exhibits wave nature. For example, in the case of f D 1MHz and
∆ f D 1 kHz, the time duration is 1 ms and the spatial length is 300 km! This
is a very long wave! However, this frequency mode may even contain only a single

108 2 Introduction to Optical Quantum Information Processing
Time
edutilpmA
edut
ilpmA
Time
Frequency
Frequency
rewoP
rewoP
(a)
(b)
Figure 2.10 Two extremes of wavepackets, (a) a frequency single mode and (b) pulsed light.
Time
edutilpmA
t
1
t
2
t
3
Figure 2.11 Atemporalmodei with the temporal function of exp(γjt t
i
j) can be extracted
from broadband continuous-wave light and defined as a qumode when the continuous light is
very weak.
photon – usually associated with a particle – which then corresponds to a 300 km
long single photon.
16)
Nonetheless, pulsed light shows particle nature of the wavepacket which is intu-
itively understandable. However, in the real situation, this is not always the case.
Pulsed light or, more precisely, a pulsed qumode can be defined even in terms of
broadband (frequency-multimode) continuous-wave light. For example, a temporal
mode i with the temporal function of exp(γjt t
i
j) can be extracted from broad-
band continuous-wave light and defined as a qumode, as shown in Figure 2.11,
when the continuous light is very weak (see Section 8.2).
16) Recall the discussion at the beginning of this chapter, where the occupation number of a qumode,
i.e., its photon number, and hence the photons themselves are a mathematical construct (to
represent the energy levels of a qumode) rather than a physical entity.
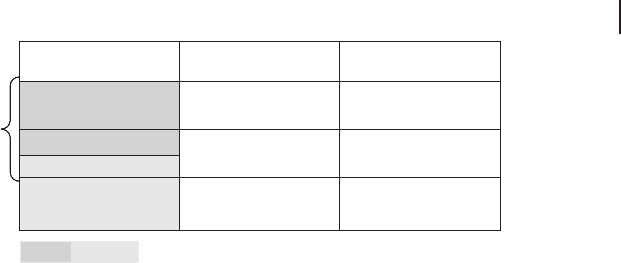
2.3 Quantum Optical Unitaries 109
cubic or higher
interaction
(Hamiltonian)
input-output relation
of mode operators
unitary transformation
displacement
in phase space
linear “scalar”
beam splitter
quadratic
linear
non-Gaussian
(cubic phase gate,
Kerr effect)
nonlinear
squeezing
tical interactions
Gaussian
linear, nonlinear op
Figure 2.12 Optical interactions and transformations in terms of the annihilation and creation
operators representing a discrete set of qumodes for the optical field.
2.3
Quantum Optical Unitaries
We shall now turn to unitary, linear and nonlinear optical manipulations of quan-
tum optical states. The discussion in this section is a continuation of the more ab-
stract introduction to unitaries and quantum computation in Sections 1.3 and 1.8,
though here, it is applied to optical systems.
In Figure 2.12, a table is shown summarizing possible optical interactions and
transformations for state preparation and man ipulation. The most accessible and
practical interactions are those described by linear and quadratic Hamiltonians,
where as before, quadratic refers to the order of a polynomial of the qumode oper-
ators Oa
k
.
In Section 2.2.8.2, we learned that an arbitrary single-qumode Gaussian pure
state is a displaced squeezed vacuum state,
O
D(α)
O
S(ζ)j0i. Similarly, an arbitrary
single-qumode Gaussian unitary that transforms a Gaussian state into a Gaussian
state is given by Eq. (1.126), supplemented by a complex phase-space displacement
O
D(α). When Eq. (1.126) is applied upon a single-mode vacuum state, the first phase
rotation
O
R(φ
0
) has no effect. The remaining position-squeezing
O
S(r)canbecom-
bined with the second phase rotation
O
R(φ) into the general, complex squeezing
operation
O
S(ζ). Therefore, an arbitrary, single-qumode Gaussian pure state is ob-
tained through an arbitrary single-qumode Gaussian unitary acting on the vacuum
state. However, a single-qumode Gaussian unitary may as well act upon an arbi-
trary single-qumode state. In this case, the exact decomposition from Eq. (1.126)
should be used, including the first phase rotation
O
R(φ
0
), together with
O
D(α).
We will shortly see that the decomposition of Eq. (1.126) corresponds to the
single-qumode case of a more general decomposition for any multi-qumode Gaus-
sian unitary. These unitary multi-mode transformations are linear and generated
from quadratic Hamiltonians. An arbitrary quadratic Hamiltonian then transforms
the optical mode operators as
Oa
0
k
D
X
l
A
kl
Oa
l
C B
kl
Oa
†
l
C γ
k
. (2.104)
