Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing

Подождите немного. Документ загружается.

110 2 Introduction to Optical Quantum Information Processing

Here, the matrices A and B satisfy the conditions AB

D (AB

)

and AA

†

C 1 according to the bosonic commutation relations. This transformation is

also referred to as the linear unitary Bogoliubov (LUBO) transformation [120]. It

combines passive (photon-number preserving) and active elements, that is, beam

splitters and squeezers, respectively; the γ

’s in Eq. (2.104) describe the phase-space

displacements.

As an example, for a single-mode position squeezer, we have Oa

DOa cosh r 

†

sinh r such that the x-quadrature would become Ox

D e

r

Ox,andthep-

quadrature Op

D e

Op, similar to Eqs. (2.53) and (2.56).

By comparing the LUBO transformation to a purely passive, linear transforma-

tion,

, (2.105)

with an arbitrary unitary matrix U, we observe that there is no mixing between

the annihilation and creation operators in the passive transformation. Despite this

difference, also the active, more general LUBO transformation is only linear in

the mode operators. Therefore, general linear optical transformations are referred

to here as LUBO transformations, including squeezers. As squeezing, however,

typically involves a nonlinear optical interaction (see Section 2.2.4), it may as well be

excluded from the “ linear-optics” toolbox (see Figure 2.12). Our more mathematical

than physical deﬁnition of linear optical transformations is motivated by the special

character of the Clifford and symplectic transformations (see Section 1.8 and next

section) with regard to quantum information processing.

As an example for Eq. (2.105), consider a general two-mode beam splitter trans-

formation in the Heisenberg picture,

( Oa

)

D U(2)( Oa

)

, (2.106)

with a unitary matrix

U(2) D



i(φCδ)

sin θ e

iδ

cos θ

i(φCδ

)

cos θ e

iδ

sin θ



. (2.107)

An ideal phase-free beam splitter operation is then simply given by the linear trans-

formation







sin θ cos θ

cos θ sin θ





, (2.108)

with the transmittance and reﬂectivity parameters sin θ and cos θ .Thus,thegen-

eral unitary matrix U(2) corresponds to two phase shifts and one phase-free beam

splitter,

U(2) D



iδ



sin θ cos θ

cos θ sin θ



iφ



. (2.109)

2.3 Quantum Optical Unitaries 111

The link between elementary quantum optical devices such as phase shifters, beam

splitters, and single-mode squeezers on one side and an arbitrary LUBO transfor-

mation as in Eq. (2.104) on the other side is provided through two important re-

sults:

 any active, multi-mode LUBO transformation as in Eq. (2.104) can be decom-

posed into a three-step circuit consisting of a passive, linear optical multi-mode

transformation as in Eq. (2.105), single-mode squeezers, and another passive,

linear optical multi-mode transformation [89], and

 any passive, linear optical multi-mode transformation described by an arbitrary

unitary matrix as in Eq. (2.105) can be realized through a sequence of two-mode

beam splitters and single-mode phase shifters [121].

The former result is on the so-called Bloch–Messiah reduction.Itcanbederived

through singular value decomposition with A D UA

†

and B D UB

unitary matrix U that simultan eously diagonalizes the two commuting Hermitian

operators AA

†

and BB

†

such that U

†

(AA

†

)U D A

and U

†

(BB

†

)U D B

unitary matrix V that simultaneously diagonalizes the two commuting Hermitian

operators A

†

A and (B

†

such that V

†

A)V D A

and V

†

V D B

and non-negative, real, diagonal matrices A

and B

, A

D B

C 1 [89]. Then,

Eq. (2.104) becomes (γ

 0)

C B

†

l, j

)

†

)

C U

)

†

)

C (B

)

†

. (2.110)

Here,

†

)

are the mode operators after the ﬁrst passive transforma-

tion according to Eq. (2.105) and Oc

D (A

)

C (B

)

†

are the squeezed

mode operators after the N single-mode squeezing transformations on every out-

put mode j of the ﬁrst circuit. The ﬁnal step is another passive transformation, this

time with matrix U.

The above two results together imply that any multi-mode LUBO transformation,

that is, any linear multi-mode transformation as in Eq. (2.104), can be implemented

with single-mode phase shifters, single-mode squeezers, and two-mode beam split-

ters. The displacements in Eq. (2.104) (the γ

’s) can be also realized using highly

reﬂective beam splitters. An example for a three-mode LUBO transformation is

showninFigure2.13.

The decomposability of the passive parts in the LUBO transformation follows

fromthefactthatanyN  N unitary matrix may be expressed as [121],

U(N) D (B

N1N

N2N

B

 B

N2N1

N3N1

B

1

. (2.111)

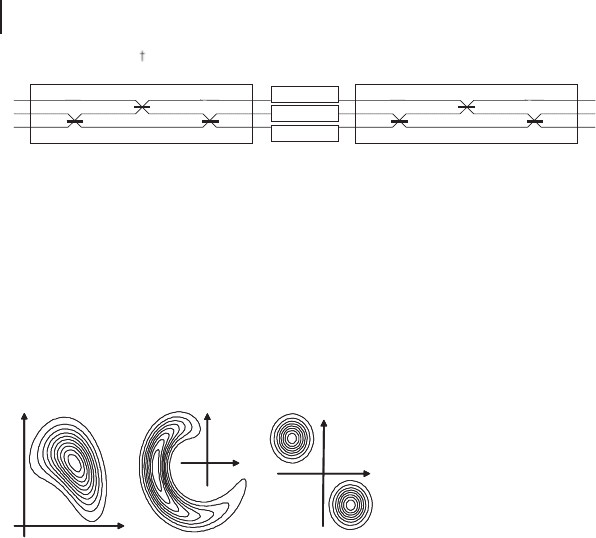
112 2 Introduction to Optical Quantum Information Processing

)3(V

passive linear optics

single-mode

squeezers

)3(U

Figure 2.13 Bloch–Messiah reduction and

“tree structure” for a general three-mode

LUBO transformation (without phase-space

displacements). Bloch–Messiah leads to a de-

composition into three blocks: a middle-block

with three single-mode squeezers (parame-

terized by three real squeezing parameters

, r

g) and two passive linear-optics

blocks, one at the beginning and one at the

end of the circuit. The tree structure for each

passive block consists of three beam splitters

with one reﬂectivity parameter and one phase

per beam splitter. Three extra phases in each

passive block (omitted in the ﬁgure) give nine

parameters for each passive circuit and, to-

gether with the three squeezers, a total of 21

parameters for the entire LUBO circuit. Note

that this decomposition is independent of the

input state.

Figure 2.14 Examples of single-mode states generated through highly nonlinear interactions.

Shown is the Q function Q(x, p ) for a Gaussian coherent state evolving into various non-

Gaussian states subject to a quartic self-Kerr interaction with

H /Oa

†

Oa( Oa

†

Oa  1).

Here, the N(N  1)/2 beam splitter operations each depend on two parameters,

the reﬂectivity/transmittance parameter and one phase, B

 B

(θ

, φ

). The

do not represent matrix elements, but N-dimensional identity matrices with

the entries I

, I

,andI

replaced by

iφ

sin θ

iφ

cos θ

,cosθ

,and sin θ

, (2.112)

respectively. Extra phase shifts are included through the diagonal matrix D with

elements e

iδ

,...,e

iδ

. For example, the unitary 2  2 matrix in Eq. (2.107)

corresponds to U(2) D (B

1

,withφ  φ

, θ  θ

, δ  δ

,andδ

 δ

A general LUBO transformation on N qumodes is then parameterized by 2N

real parameters for the two passive networks and N real squeezing parameters,

apart from the phase-space displacements. When acting upon an N-mode vacuum

state, the ﬁrst passive network has no effect, and hence N

CN parameters sufﬁce

to represent any (zero-mean) N-mode Gaussian pure state.

As shown in Figure 2.12, going beyond the regime of linear resources and oper-

ations means to include cubic or higher-order interactions leading to nonlinear trans-

formations. Such a nonlinear interaction would normally map a Gaussian state on-

to a non-Gaussian state described by non-Gaussian Q and Wigner functions, see

Figure 2.14. These interactions are typically very weak; an example would be the

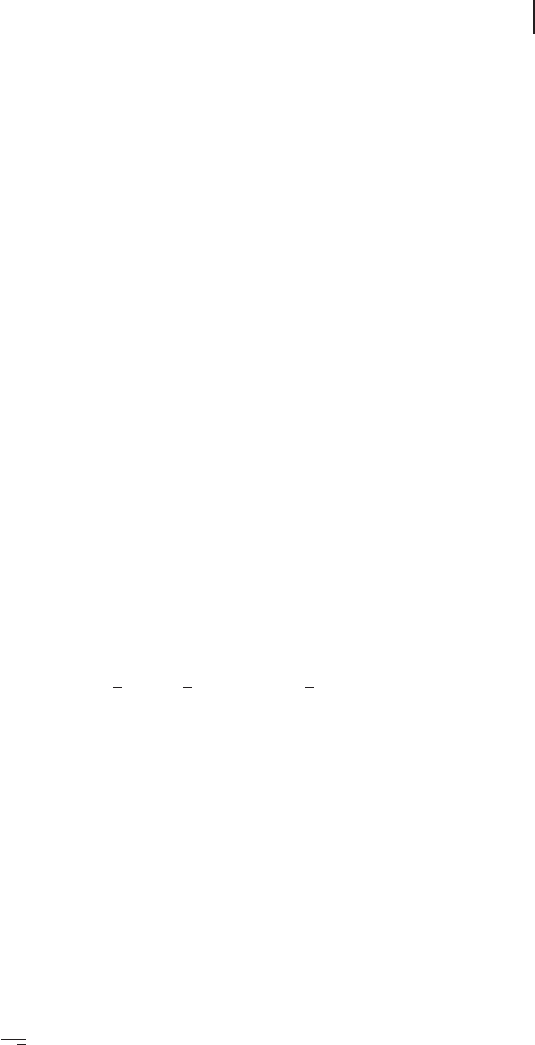
2.4 Gaussian Unitaries 113

extremely weak Kerr effect in an optical ﬁber. Therefore, for sufﬁciently long in-

teraction times, unwanted photon losses will normally dominate over the desired

nonlinear transformation.

In the following section on Gaussian unitaries in form of phase-space displace-

ments and symplectic transformations, we shall see that the transformation rules

for the Wigner function are particularl y simple for Gaussian unitaries.

2.4

Gaussian Unitaries

In the preceding section, we showed that a multi-qumode LUBO transformation

is a linear transformation of the mode operators, as described by Eq. (2.104), de-

composable into phase-shift, beam-splitter, and squeezing transformations supple-

mented by phase-space displacements. Such Gaussian unitaries, omitting the local

shifts of the ﬁrst quadrature moments, can be most conveniently expressed on

the level of the correlation matrices. In this case, they correspond to the symplectic

transformations,

(N)

! V

(N)

D SV

(N)

, (2.113)

with the 2N2N real matrices S 2 Sp(2N, R ). For unitarity and in order to preserve

the commutators, we have the condition S ΛS

D Λ,as

i, j



S Λ S



, (2.114)

using the linear transformation of the phase-space operators,

D S

with

ξ from Eq. (2.91). Similar to the LUBO transformations, the symplectic transfor-

mations depend on 2N

C N real parameters. Those transformations which are

both symplectic, O ΛO

D Λ, and orthogonal, OO

D 1,belongtotheclassof

passive transformations,

17)

as described by Eq. (2.105) in terms of the evolution

of the mode operator. Recall that these transformations, realizable through beam

splitters and phase shifters alone, are photon-number preserving, leaving TrV

(N)

invariant.

Important examples of symplectic transformations are the passive 50/50 two-

qumode beam splitter,

10 1 0

01 0 1

1010

01 0 1

, (2.115)

17) They form a compact subgroup of Sp(2N, R)withelementsO 2 Sp(2N, R) \ O(2N ).

114 2 Introduction to Optical Quantum Information Processing

and the active single-qumode x and p squeezers,

XSQ



r



, S

PSQ



r



, (2.116)

respectively. Similar to the Bloch–Messiah reduction of arbitrary LUBO transfor-

mations, as derived in Eq. (2.110), an arbitrary S 2 Sp(2N, R)canbedecomposed

S D O

kD1



r



, (2.117)

with orthogonal N-mode transformations O, O

and single-mode position squeez-

ing r

for every qumode. This is sometimes referred to as Euler decomposi-

tion of symplectic transformations. Next, we shall now turn to quantum optical

non-unitaries, that is, channels and measurements in the quantum optical set-

ting.

2.5

Quantum Optical Non-unitaries

We are now in a position to apply the general irreversible quantum operations as

introduced in Section 1.4 to quantum optical systems. We shall ﬁrst consider CPTP

maps, that is, quantum optical channels, and then quantum optical measurements

(CPTD maps). Finally, we will discuss the important Gaussian channels and mea-

surements.

2.5.1

Channels

C onsider again the scenario illustrated in Figure 1.5. The signal and ancilla systems

are now supposed to be represented by some quantum optical states, and the global

unitary

will be a certain optical interaction generated by some Hamiltonian

polynomial of the qumode operators. The trace over the ancilla then gives the signal

state subject to the corresponding reduced dynamics.

For example, a one-photon signal state j1i

DOa

†

j0i

would partially leak into

a vacuum ancilla mode ( O

Dj0i

h0j) through a beam splitter unitary, Oa

†

j0i

ηj10i

1  ηj01i

, using the deﬁnitions cos

θ  η and sin

θ 

1  η, similar to Eq. (2.108). Tracing over the ancilla mode leads to the ﬁnal signal

state ηj1i

h1jC(1η)j0i

h0j. This simple model describes, for instance, the trans-

mission of a single photon through a lossy channel with transmission parameter

η D exp(L/L

att

) and the channel attenuation length L

att

A general photonic single-rail qubit together with a vacuum ancilla, (α C

β Oa

†

)j0i

˝j0i

, is transformed into αj00i

C β

ηj10i

C β

1  ηj01i

2.5 Quantum Optical Non-unitaries 115

This can be recast in terms of Kraus operators as

O

!O

kD0

O

†



jαj

αβ



β jβj



†



jαj

αβ



β jβj



†



jαj

1  γαβ



1  γα



β (1  γ)jβj





γjβj





αj0i

C β

ηj1i





h0jCβ



h1j



Cjβj

(1  η)j0i

h0j , (2.118)

with



1  γ







, (2.119)

using



hkj

j0i

in the Fock basis, γ  sin

θ D 1  η,andthebeam

splitter unitary

D e

θ (Oa

†

Oa

†

)

. The amplitude of the one-photon component

is always attenuated and as the photon can be absorbed by the ancilla, we obtain

for the signal output state an incoherent mixture of the attenuated input state and

a vacuum noise term.

Consider now for the signal system a single qumode in an initial coherent state

jαi

. Importantly, as the only optical state, the coherent state remains a pure

coherent state after the action of the generalized amplitude damping channel,

kD0

O

†

, with Kraus operators

nDk

nk

(1  η)

jn  kihnj , (2.120)

for which we obtain

jαi

1  η

(1η)jαj

ηαi

, (2.121)

using Eq. (2.43). Eventually, we have

kD0

jαi

hαj

†

ηαi

ηαj . (2.122)

This is the expected result according to the beam splitter transformation jαi

j0i

ηαi

˝j

1  ηαi

, corresponding to the signal map jαi

ηαi

Although the coherent state remains pure, its amplitude gets attenuated exponen-

tially with η D exp(L/L

att

) in the case of a channel transmission.

The lossy beam splitter channel discussed so far, describing the effect of photon

losses in a very simple way, is certainly the most important imperfection in optical

116 2 Introduction to Optical Quantum Information Processing

quantum information processing. As it corresponds to a quadratic interaction (the

beam splitter) together with a Gaussian ancilla state (the vacuum, or, more general-

ly, any Gaussian ancilla state), it will always map Gaussian signal states to Gaussian

signal states – it is a Gaussian channel (see Section 2.6).

In the Heisenberg picture, the reduced dynamics may be calculated using the

dual, CPUP map, as introduced in Section 1.4.1 in Eq. (1.76), with the Kraus op-

erators depending on the global unitary and the initial ancilla state. For the above

example of the beam splitter model, we obtain



( Oa

) D

†

h0j

†

jki

hkj

j0i

h0j

†

j0i

h0j



η Oa

1  η Oa



j0i

η Oa

, (2.123)

using Oa

j0i

D 0. Note that now [E



( Oa

), E



( Oa

†

)] D η, indicating the non-unitarity

of the evolution. The reduced dynamics here, corresponding to a Gaussian chan-

nel, map the generators Ox and Op, and linear combinations of them such as Oa,into

another linear combination of Ox and Op. In Section 2.6, we will see how to recast

this using the covariance formalism. Channels with global unitaries generated by

Hamiltonians with an order h igher than quadratic or those with non-Gaussian an-

cilla states will, in general, lead to nonlinear evolution equations.

2.5.2

Measurements

Now, for the case of CPTD maps in form of photon measurements on optical states,

we shall again ﬁrst consider a photonic qubit (qudit) and later a photonic qumode.

The photon measurements will either project onto the Fock basis jnihnj (using

photon-number resolving detectors) or, more realistically, they will only discrim-

inate between the vacuum and the non-vacuum state which is described by the

binary POVM

Dj0ih0j and

D 1 j0ih0j.

Let us consider the very general case of all those POVMs where the signal states

only contain one photon. In this case, any unitary operation (gate) can be accom-

plished with linear optics [121]. This statement applies to arbitrary qudit states

where each basis vector of the qudit is described by one photon occupying one

of d modes, Oa

†

j0i, i D 1...d (so-called “multiple-rail encoding ”). It can be under-

stood by looking at the corresponding Naimark extension of the POVM introduced

in Section 1.4.2. The POVM is then described by a von Neumann measurement

onto the orthogonal set

iDju

iCjN

i , (2.124)

in a Hilbert space larger than the original signal space.

2.6 Gaussian Non-unitaries 117

In the multiple-rail encoding, this leads to an orthogonal set of vectors

j D1

µ j

†

j0i , (2.125)

with a unitary N  N matrix U having elements U

µ j

. The application of a linear-

optics transformation V to this set (in order to project onto it) can be written as

i!jw

j,kD1

µ j



†

j0iD

kD1

µk

†

j0iDOa

†

j0i , (2.126)

choosing V  U. As a result, when detecting the outgoing state, for every one-

photon click in mode µ, one can unambiguously identify the input state jw

As an example, the linear-optics implementation of the POVM for the optimal

USD of the non-orthogonal states in Eq. (1.87), using one-photon signal states and

multiple-rail encoding, j

0ij100i, j

1ij010i, j

2ij001i,canbedirectlyob-

tained. In this case, the output states after the linear-optics circuit, j100i, j010i,and

j001i, uniquely refer to one of the three orthogonal states jw

i, and hence identify

the signal states jχ

i and jχ



i with the best possible probability.

For states other than one-photon states, it is generally not obvious whether a

given POVM can be implemented with linear optics. There are important examples

for which the exact POVM cannot be implemented by linear optics such as the Bell

measurement on two dual-rail encoded photonic qubits [122].

Now, considering a single qumode, remarkably, there is also a very simple linear

optical scheme for the USD of two arbitrary coherent states such as fj˙αig(see Fig-

ure 2.9 at the beginning of Section 2.2.8) that achieves the quantum mechanically

optimal USD for two pure non-orthogonal states fjψ

i, jψ

ig [123]. In this case, the

success probability for a conclusive result equals 1 jhψ

jψ

ij D 1 jhαjαij D

1  exp(2α

) (assuming α real) [30–32]. The detectors only have to discriminate

between the vacuum and non-vacuum components at the output ports of the beam

splitter, where the two possible states are either j

2α,0ior j0, 

2αi,andonlythe

term j0, 0i is ambiguous. This scheme can also be formulated using the Naimark

extension, however, in this case, the signal and Naimark vectors must be expressed

in terms of more complicated superpositions of coherent states (see Chapter 8).

2.6

Gaussian Non-unitaries

Gaussian channels (Gaussian CPTP maps) may be most conveniently expressed

in terms of covariance (correlation) matrices. One can show that a general multi-

qumode Gaussian channel acts on the level of the covarian ce matrices as [124]

(N)

D FV

(N)

C G , (2.127)

118 2 Introduction to Optical Quantum Information Processing

whereforthechanneltobephysical,the2N  2N matrices F and G must satisfy

the condition

16 det G  (det F  1)

. (2.128)

The special case of reversible, unitary, symplectic transformations is again obtain ed

when G D 0 (the zero matrix) and F D S 2 Sp(2N, R)withdetS D 1.

Let us again consider the effect of a lossy channel, as described by the beam split-

ter model in Section 2.5.1. Since the signal mode operator transforms as Oa

η Oa

1  η Oa

through the beam splitter and, similarly, Ox

η Ox

1  η Ox

and Op

η Op

1  η Op

,weobtain

(1)

! V

(1)

D ηV

(1)

C (1  η)



η 0



(1)



η 0



C (1  η)

1 , (2.129)

assuming that the ancilla mode started in the vacuum state. Note that, in gener-

al, the excess noise matrix G depends on the initial ancilla state. We can read off

the F and G matrices and obtain det G D (1  η)

/16 and det F D η,suchthat

16 det G D (1  η)

D (det F  1)

. We ﬁnally note that in the covariance formal-

ism, the reduced dynamics are expressed simply by the corresponding signal sub-

matrix of the globally transformed signal-ancill a covariance matrix after discarding

the ancilla submatrix. The signal submatrix is a valid covariance matrix since the

global transformation such as, for instance, Ox

η Ox

1  η Ox

,isunitary

and hence preserves the commutators. This is different from the non-unitary, dual

map Ox

! E



( Ox

) D

η Ox

Let us now brieﬂy discuss the important linear, Gaussian measurements which

are well approximated by means of so-called homodyne detectors.Inthiscase,in-

stead of the discrete photon numbers, the rotated quadrature observables are mea-

sured. A photodetector measuring an electromagnetic mode converts the photons

into electrons and hence into an electric current called the “photocurrent”

i.We

may then assume

i /On DOa

†

Oa or

i D q Oa

†

Oa with q a constant. In order to detect

a quadrature of the mode Oa, the mode must be combined with an intense “local

oscillator” at a 50/50 beam splitter. The local oscillator is assumed to be in a co-

herent state with large photon number, jα

i. I t is therefore reasonable to describe

this oscillator by a classical complex amplitude α

rather than by an annihila-

tion operator Oa

. The two output modes of the beam splitter, ( Oa

COa)/

2and

( Oa

Oa)/

2, may then be approximated by

D (α

COa)/

2, Oa

D (α

Oa)/

2 . (2.130)

This yields the photocurrents

D q Oa

†

D q





COa

†



(α

COa)/2 ,

D q Oa

†

D q





Oa

†



(α

Oa)/2 . (2.131)

2.6 Gaussian Non-unitaries 119

The actual quantity to be measured is the difference photocurrent

i 



D q





Oa C α

†



. (2.132)

By introducing the phase Θ of the local oscillator, α

Djα

jexp(iΘ), we can see

that any quadrature Ox

(Θ)

from Eq. (2.35) can be measured when the local oscilla-

tor’s phase Θ 2 [0, π] is adjusted accordingly. A possible way to realize quantum

tomography [113] by reconstructing the Wigner function relies on this measure-

ment.

Gaussian operations

Gaussian channels:

(N)

D FV

(N)

C G ,16detG  (det F  1)

Gaussian unitaries:

LUBO transformation: Oa

C B

†

(Cγ

)

Bloch–Messiah reduction:

A D UA

†

, B D UB

, U

†

U D 1 , V

†

V D 1

l, j

)

†

)

C U

)

†

(Cγ

)

passive linear transformation:

A ! U , U

†

U D 1 , B ! 0 W

symplectic transformation:

F ! S , G ! 0 W

(N)

D SV

(N)

, S ΛS

D Λ ,detS D 1, 8S 2 Sp(2N, R)

Euler decomposition:

S D O

kD1

XSQ

passive, orthogonal, symplectic transformation:

O ΛO

D Λ , OO

D 1