Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing

Подождите немного. Документ загружается.

120 2 Introduction to Optical Quantum Information Processing

2.7

Linear Optics: Possibilities and Impossibilities

CV Gaussian resources can be unconditionally prepared in the laboratory and

Gaussian operations are deterministic and experimentally efﬁcient. Nonetheless,

there are various, highly advanced tasks in quantum information which would

require a non-Gaussian element:

 quantum error detection and correction for qumodes are impossible i n the

Gaussian regime [93, 125–127],

 universal quantum computation on qumodes and quantum computational

speed-up through it are impossible in the Gaussian regime [86, 90].

The former of these two important results can be understood by realizing that

Gaussian channels (e.g., the lossy channel described in the preceding sections)

typically lack the stochastic nature of those channels for which the standard quan-

tum error correction codes are designed (recall Section 1.9). Amplitude damping

is an error that will occur in every optical transmission line of an encoded state. In

this case, although for photonic qubits, stabilizer codes help, for photonic qumodes

encoded into Gaussian states, the CV stabilizer codes have no effect.

18)

The latter

result above is related with the Gottesmann–Knill theorem for CV qumode sys-

tems. It fully applies to physical, Gaussian stabilizer states (see Sections 1.8, 2.2.8.1,

and 3.2.2) and their manipulation through Gaussian operations.

The necessary non-Gaussian element may be provided in form of a DV measure-

ment such as photon counting. There are also a few simpler tasks which can be

performed better with some non-Gaussian element compared to a fully Gaussian

approach, for instance, quantum teleportation [128] or optimal cloning [129, 130]

of coherent states.

Similarly, in the DV regime, (efﬁcient) universal quantum computation on pho-

tonic qubits would depend on some nonlinear element, either directly implement-

ed through nonlinear optics or induced by photon measurements (see next section

and Chapters 7 and 8). In addition, there are even supposedly simpler tasks which

are impossible, using only quadratic interactions (linear transformations) and stan-

dard DV measurements such as photon counting. The prime example for this is

a complete photonic Bell measurement (see Sections 1.5 and 1.6) on two photonic

dual-rail qubits [122, 131].

In contrast, in the CV regime, a photonic Bell measurement onto the CV Bell

basisoftwoqumodesasgivenbyEq.(1.95)isverysimple:measuringthetwo

stabilizer eigenvalues u DOx

Ox

and v DOp

COp

only requires a 50/50 beam

splitter and two homodyne detectors. N ow, recall that any POVM is effectively a von

Neumann, projection measurement in a higher-dimensional Hilbert space (com-

pared to the signal space, see Section 1.4.2). The CV Bell measurement turns out

18) Nonetheless, in Chapter 5, an experiment will be described in which a nine-qumode stabilizer

code was realized; this code can still be useful for protecting a qumode against non-Gaussian

error channels different from the Gaussian amplitude-damping photon-loss channel.

2.8 Optical Quantum Computation 121

to be a two-qumode projection measurement that corresponds to a single-qumode

POVM, namely,

D (1/π)jαihαj with α D u Civ. This is also the POVM for the

optimal coherent-state estimation, equivalent to a so-called Arthurs–Kelly measure-

ment [132]. An Arthurs–Kelly measurement is effectively an attempt to simultane-

ously detect position and momentum; and optically this can be realized by splitting

the mode of interest at a 50/50 beam splitter and detecting the position at one out-

put and the momentum at the other output. The input mode of the “unused port”

of the beam splitter, playing the role of an ancilla, would (ideally) start in a vacu-

um state. The signal POVM

is then equivalent to the signal-ancilla projectors

jΨ (u, v)ihΨ (u, v)j with the CV Bell states o f Eq. (1.95) [133].

It is worth pointing out that the above restrictions and no-go results apply even

when linear elements and photon detectors are available that operate with 100%

efﬁciency (i.e., every photon is counted) and 100% reliability (i.e., every photon is

counted correctly). In other words, the imposed constraints are of fundamental

nature and cannot be circumvented by improving the experimental performance

of the linear elements, for example, by further increasing the squeezing levels.

2.8

Optical Quantum Computation

A necessary criterion for a quantum computer to give a true advantage over classi-

cal computers is that its realization does not require exponential resources. In oth-

er words, the exponential “speed-up” quantum computation it is usually associated

with must not be at the expense of an exponential increase of physical resources

(see Section 1.8). The exponentially large dimension of the Hilbert space of N logi-

cal qubits, 2

, should be exploited with a number of physical resources scaling as

 N (or a polynomial of N) rather than  2

Both for qubit and qumode computations, there is always at least one universal

gate of those gates discussed in Section 1.8 which is not realizable through linear

transformations alone. In single-photon single-rail encoding, even a single-qubit

Hadamard gate, tran sforming a Gaussian vacuum state into a non-Gaussian su-

perposition of vacuum and one-photon Fock state would be highly nonlinear. The

hardest part of universally processing dual-rail encoded qubits would be the en-

tangling gate which has to act upon at least two photons. Ultimately, the universal

processing of even a single qumode requires some form of nonlinearity.

The most obvious approach now to optically implement an entire set of universal

quantum gates would be d irectly through nonlinear interactions. The two-qubit C

gate from Section 1.8 is accomplished by applying a quartic cross-Kerr interaction

on two photonic occupation number qubits,

exp



iπ Oa

†

˝Oa

†



jki˝jliD(1)

jki˝jli . (2.133)

The same interaction leads to a C

gate for two photonic dual-rail qubits, with the

cross-Kerr interaction acting on the second rail (mode) of each qubit such that only

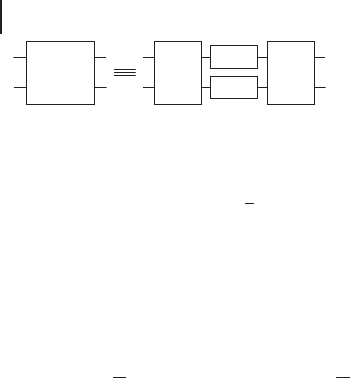
122 2 Introduction to Optical Quantum Information Processing

BSBS

CKCK

Figure 2.15 Implementing a controlled sign

gate (C

) on two single-rail qubits using

cross-Kerr (CK) or self-Kerr (SK) nonlineari-

ties. The ﬁrst beam splitter (BS) transforms

the term j11i into (j20ij02i)/

2, while

the other terms stay in the vacuum and one-

photon space. As the SK interactions affect

sign ﬂips only for the two-photon compo-

nents, only the term j11i acquires a sign ﬂip.

the term j01i˝j01i acquires a sign ﬂip. This is the conceptually simplest and,

in theory, most efﬁcient method to complete the set of universal gates in dual-rail

encoding. In the low-photon number subspace here, we may even decompose the

cross-Kerr two-mode unitary into a beam splitter, two self-Kerr one-mode unitaries,

exp

†



†

 1

i

˝ exp

†



†

 1

i

, (2.134)

and another beam splitter (see Figure 2.15). Thus, a sufﬁciently strong one-mode

self-Kerr interaction would be enough to fulﬁll the criteria for DV universality

on the ﬁnite-dimensional multi-qubit subspace of the inﬁnite-dimensional, multi-

mode optical Fock space. At the same time, the quartic one-mode self-Kerr in-

teraction together with Gaussian, linear transformations (LUBO transformations)

would also be sufﬁcient for the strong notion of full (asymptotically arbitrarily pre-

cise) CV universality, as expressed by Eq. (1.119).

The problem of this approach, however, is that an effective coupling strength of

 π for the self/cross-Kerr interactions is totally infeasible on the level of single

photons. Therefore, it is worth examining carefully if there is a way to implement

universal quantum gates through linear optical elements, ideally just using beam

splitters and phase shifters. A very early proposal for linear-optics-based quantum

computation indeed does work with only linear elements [134]. It is based upon

multiple-rail encoding, as introduced earlier in the context of optical POVMs. The

multiple-rail scheme encodes a d-level system into a single photon and d optical

modes, with the basis states Oa

†

j00 0i, k D 1,2,...,d. Any unitary operator can

be realized in the space spanned by this basis as we only need

U Oa

†

j00 0iD

lD1

†

j00 0i , 8k D 1,2,...,d . (2.135)

This linear transformation, as in Eq. (2.105), is easily achieved through a sequence

of beam splitters and phase shifters [121]. The realizability of any POVM is then

an obvious consequence of the implementability of any unitary operator on one-

photon states.

As a result, universal quantum computation is, in principle, possible using a

single photon and linear optics. This kind of realization would be clearly efﬁcient

from an experimental point of view. In fact, implementing a universal two-qubit

gate in a d D 2

D 4-dimensional Hilbert space would only require the modest

set of resources of an optical “ququart”, in “quad-rail ” encoding corresponding to

2.8 Optical Quantum Computation 123

a single photon and four optical modes. In fact, for small quantum applications,

by adding to the polarization of the photons (their spin angular momenta) extra

degrees of freedom such as orbital angular momenta, this kind of approach can be

useful [135].

Nonetheless, the drawback of the multiple-rail-based linear-optics quantum com-

puter [134] is its bad scaling. Even in theory, this type of quantum computer is

inefﬁcient. Scaling it up to computations involving N qubits, we need 2

basis

states and hence 2

optical modes. All these modes have to be controlled and pro-

cessed in a linear optical circuit with an exponentially increasing number of optical

elements. For example, a 10-qubit circuit would only require 10 photons and 20

modes in dual-rail encoding, while it consumes 2

D 1024 modes (for just a sin-

gle photon), and at least as many optical elements in multiple-rail encoding.

More recently, there are now conceptually very different approaches to obtain the

necessary nonlinear elements. One such approach uses measurement-induced

nonlinearities and can be incorporated into quantum information protocols

through gate teleportation (see Chapter 6) or, ultimately, in the form of one-way

cluster computations (see Chapter 7). Another important and promising concept is

that of using weak nonlinear interactions which are experimentally accessible and

still, in principle, sufﬁcient for universal quantum information processing (see

Chapter 8).

Part Two Fundamental Resources and Protocols

127

Entanglement

Entanglement is an essential resource for quantum information processing. In

quantum optics, typically, nonlinear optical interactions such as parametric down

conversion (PDC) are employed to create photonic entangled states. In the para-

metric approximation, the signal-idler twin beam generation is described by a

quadratic Hamiltonian, which, according to our deﬁnition, corresponds to a linear

transformation.

Hence, linear transformations, though insufﬁcient for universal quantum infor-

mation processing on qubits or qumodes, are enough to prepare entangled states of

light. Then, typically, the creation of photonic qubit entanglement relies upon some

heralding mechanism, that is, the entangled states can be prepared only condition-

ally. In contrast, the Gaussian entangled states of optical qumodes can emerge un-

conditionally from linear optical transformations. In this case, the PDC interaction

can be used to directly obtain entangled two-mode squeezed states. Alternatively,

individually squeezed qumodes may be entangled through beam splitter transfor-

mations.

From a theoretical point of view, it turns out that there is a link between the sta-

bilizers (Section 1.9) that uniquely determine an entangled state and the witnesses

(Section 1.5) that may be used to unambiguously verify the presence of entangle-

ment in that state. This link can be established both for qubits and qumodes.

In this chapter, we shall ﬁrst focus on qubit entanglement (Section 3.1), includ-

ing an overview of various types of entanglement such as bipartite and multipar-

tite entanglement, and some explicit entanglement witnesses for qubit entangled

states (Section 3.1.1). Further, we will deﬁne qubit cluster states and qubit graph

states as a rather general notion of multi-party entanglement (Section 3.1.2). In

Section 3.1.3, we will then describe a selection of experiments in which qubit EPR,

GHZ, and cluster states were realized.

The CV qumode counterparts of the qubit entangled states will be discussed in

Section 3.2, including a few distinct features of graph states in the CV regime;

in particular, the connection between complex-valued stabilizers/nulliﬁers for

qumodes, complex-weighted qumode graph states, and mul ti-mode Gaussian pure

states (Section 3.2.2). A selection of experiments is presented in Section 3.2.3.

Quantum Teleportation and Entanglement. Akira Furusawa, Peter van Loock

ISBN: 978-3-527-40930-3

128 3 Entanglement

3.1

Qubit Entanglement

3.1.1

Characterization and Witnesses

In a realistic experiment, the entangled states will be always imperfect, correspond-

ing to noisy, mixed entangled states. In this case, it is useful to measure entangle-

ment witnesses which may still be able to detect entanglement for not too noisy

states. There are various references, for instance, [136–138], which provide good

reviews on general entanglement theory, including the bipartite (two-party) and

multipartite (N-party with N > 2) cases, and covering important notions such as

inseparability, witnesses, and distillability, with a focus on ﬁnite-dimensional DV

systems and qubit states.

3.1.1.1 Two Parties

In Section 1.5, we introduced the maximally entangled Bell basis for two qubits as

well as for two qumodes, general pure and mixed entangled states, inseparability

criteria, entanglement witnesses, and some examples of entanglement measures.

The discussion there was restricted to the bipartite case of two entangled subsys-

tems.

Let us now continue the discussion on entanglement witnesses for two-qubit

density operators. Recall that the partial transpose criterion (Section 1.5) is neces-

sary and sufﬁcient for detecting the entanglement of two-qubit states. Therefore,

any inseparable state O

of two qubits A and B has at least one negative eigenvalue



such that Tr( O

jφihφj) D λ



< 0, where the superscript T

denotes partial

transposition on qubit B and jφi is the corresponding eigenvector with eigenvalue



. Then, since for any pair of matrices C and D,Tr(C

D) D Tr( CD

), we also

have Tr( O

jφihφj

) D λ



< 0. Thus, by deﬁning

W jφihφj

, (3.1)

we immediately obtain a valid entanglement witness W that detects the insepa-

rability of O

,Tr(O

W ) D λ



< 0 and correctly gives Tr(

W )  0forany

separable state

since

must have positive partial transposition and hence

Tr(

W ) Dhφj

jφi0. The witness W detects every entangled state of two

qubits as partial transposition is necessary and sufﬁcient in this case.

An example for the witness in Eq. (3.1) is given by

W D

0001

0100

0010

100 0

, W

00 00

0110

0 110

00 00

, (3.2)

where jφiD(j10ij01i)/

2 is the eigenvector for the partially transposed Bell

state jΦ

i from Eq. (1.93) with Tr(jΦ

ihΦ

jφihφj) Dhφj(jΦ

ihΦ

)jφi

3.1 Qubit Entanglement 129

D1/2 < 0 and hence also Tr(jΦ

ihΦ

jjφihφj

) D1/2 < 0. This witness

clearly detects the entanglement of the Bell state jΦ

i. An alternative way to write

the witness W in Eq. (3.2) is W D 1/2 jΦ

ihΦ

j, from which one can see that

W also detects the presence of entanglement for states that deviate from jΦ

isuch

as O D (1  p)jΦ

ihΦ

jCp 1/4. The term 1/2 in W comes from the maximal

squared overlap between jΦ

i and all pure separable states.

For our discussion here, it is useful to understand the connection of the entan-

glement witnesses with the stabilizers of an entangled state. Now, the projector of

any N-qubit stabilizer state jψi can be written as [5 ]

jψihψjD

g2S

g D

kD1

(1 C g

)/2 , (3.3)

where the sum goes over all the 2

elements of the state’s stabilizer group S,while

the product only goes over all of its N generators. Thus, for N D 2, the witness

W D 1/2 jΦ

ihΦ

j can be expressed in terms of local Pauli operators, that is,

the stabilizers of jΦ

i, S DhXX, ZZi (see Section 1.5). For N D 2, this is ﬁne,

but for larger N (see next section), the number of terms in the sum in Eq. (3.3)

grows exponentially; and the product may also be an unnecessarily complicated

function of the stabilizer generators.

However, there are simpler ways to write an entanglement witness in terms of

stabilizers [139]. For instance, the following witness,

W D 1  X ˝ X  Z ˝ Z , (3.4)

detects entangled states in the vicinity of jΦ

i because we have

(

XXC ZZ

)

D 2,

(3.5)

such that Tr(jΦ

ihΦ

jW ) D1. This is the simplest linear witness, and nonlin-

ear reﬁnements (i.e., additional nonlinear correction terms) may lead to even better

witnesses [40] (see Figure 1.6). Note that the stabilizers that uniquely deﬁne the en-

tangled Bell state can also be used to detect its entanglement as their expectation

values indicate the quantum correlations for two non-commuting Pauli operators

inherent in that state. Next, we shall now consider multipartite entangled states of

more than two qubits.

3.1.1.2 Three or More Parties

First, we must consider pure states. In general, there is no Schmidt decomposi-

tion for the case of more than two parties directly obtainable as for the two-party

case. Nonetheless, there is one important representative of multipartite entangle-

ment which is reminiscent of a Schmidt decomposition, namely, the Greenberger–

Horne–Zeilinger (GHZ) state [140]

jGHZiD

(

j000iCj111i

)

, (3.6)