Фотиади Э.Э. (ред.) Геология и математика
Подождите немного. Документ загружается.


50
Гл.
11.
J{ЛДССUФUl>ац
ult
.....
'"
~
"1
________
",,_
м
I.t:)
~
.....
-----
.....
~
лы
е»};
и
4
«(изменение
по
разрезу»)
-
=
{«сквозные»,
<<Погребенные
»,
<<Наве
шенные»,
«дисгармоничные»,
«смешан
ные»}
14).
В
данном
частном
случае
представ
ление
[А
:
и]
ст
рочками
показано
в
табл.'2
.
3
.1.
В
табличном
виде
такая[А:
:U]выглядит
таК,как
показано
в
табл.
2.3.2.
Дерево
или
граф
[А
:
u]
в
этом
,
частном
случае
дается
рис.
2.3.1.
Перейдем
к
представленИI()
[А
:
и]
в
функциональном
виде.
Не
зависимые
двоичные
переменные,
при
нимающие
значени
е
О
и
1,
будем
обо
значать
через
Xi .
ДЛЯ
Х
;
И
его
отри-
цания
введем
обозначение
xi
i
,
где
0",
может
принимать
значение
О
или
1,
причем
считается,
что
X~
=
Xi,
Х
}
=
Xi-
Й
'
О
'
о'
Выра
жение
Xi,"&
Xi."
& ...
&Х;
'/',
г
де
&-
• r
знак
логического
умножения,
будем
'
называть
элементарной
конъюнкцией~
а
число
r
назовем
ее
рангом.
Набору
признаков
U
i
= (
ui,
и~,
...
• • • ,
U~
(i)
I
приведем
в
соответствии
дво
ичные
переменные
X j" X j"
•••
,
Xjpi'
где
Р
;
= log2
fi
(i),
а
;i
(i) > n (i)
являет
ся
ближайшим
числом
к
n (i),
рав
ным
числу
2
в
ц
елой
положительной
степени.
Из
X j
,'
Xj"
•••
, X j
pi
образуем
2
Pi
различных
элемен
тарных
конъ
юнкций
ранга
р
и),
которые
обозна
чим
через
p~,
k = 1, 2, ... , 2
Pi
•
"Уста
новим
взаимно
однозначное
соответ-
ствие
между
признаками
и:"
Е
и
;
и
P
t.
Будем
считать
,
что
эти
опера
ции
проделаны
дл
я
i . 1,2, ... , l.
14
)
Так
как
~крупнейmие
платформен
ные
складчатые
структ
уры»
в
соответствиИ/
с
[60]
не
М0ГУТ
быть
«ПогребеннымИ»,
«на
ве
шенными»,
~дисгармоничнымИ»,
в
дальней-
шем
считается,
:что
И
4
=
{и~,
и~}.

§ 3.
Способы
nр
едс
т
авлений
lfлассифUl;ациЙ-nере.шсл
е
llllit
5·1
Каждому
классу
A
s
поставим
в
соответствие
элементарную
конъюнкцию
Р
•
= P
J
, &
Pj
, &
'"
& P
}l'
где
Р
;'"
-
элеме
нтар
ная
конъюнкция,
поставленная
во
взаимно
одно
знаqное
соот
в
е
тствие
тому
признаку
uI
;,
Е
И
" ,
которы
й
принима
е
т
значение
1
на
а
Е
A
s
•
Таким
образом,
классу
A
s
будет
поставл
е
на
в
соо
т-
2
----1f--------~--------~--------~----
Ри
с.
2
.3
.
1.
ветствие
булева
функц
ия
Г
=
x~'
& x"i & ... &
x~P
,
где
Р
=
1
=
2}
Pi'
Набор
таких
характеристических
функц
ий
/,
',
которые
i= 1
попарно
ортогональны,
fi & f j =
О,
i
=1=
j,
и
будем
пр
ед
став-
лять
[А
:
И]
в
функционал
ьном
вид
е
.
В
рассматриваемом
ча
стном
случае
Р1
= 1, pz = 1,
Р
з
= 2,
Р
4
= 1.
Имея
в
виду
Иl,
поставим
ему
в
соотв
е
тствие
Х
1
,
и~
будет
отвечать
X
1
,
а
и~
-
Х
1;
И2
пос
тавим
в
соотв
е
тстви
е
Х2,
и~
будет
отвечать
Х2,
и:
-
Х
2;
ИЗ
по
ставим
в
соответствие
Ха,
3
б
&
З
&
-:-
3 - & . И
4
Х
4,
U
1
удет
отвечать
Хз 'Х4,
и
2
-
Хз
Х4,
и
з
-
Хз
'Х4,
поставим
в
соответстви
е
Х
6
,
и~
будет
отвечать
Х5,
и:
-
ХО.
Например,
для
Аз
получим
j3
= X
1
&
Х2&ХЗ
&
Х4&
Х
о
'
Ниж
е
при
водится
явный
вид
jS, S = 1,2, ... , 24.
Зн
а
к
логического
умно
жения
&
для
сокращения
записи
опущен.
/1
=
ХI
Х
2
Х
З
Х
4
Х
S;
/2 =
ХI
Х
2
Х
З
Х
4
Х
6;
/3
=
ХI
Х
2
Х
З
Х
4
Х
S;
/4
=
ХI
Х
2
Х
З
Х
4
Х
S
;
/6
=
ХI
Х
2
Х
З
Х
4
Х
S;
/6 =
ХIХ2
Х
З
Х
4
Х
S;
Г
=
ХI
Х
2
Х
З
Х
4
Х
S;
/8
=
Хl
'Х
2
Х
З
Х
4
Х
S;
/9
=
ХI
Х
2
Х
З
Х
4
Х
S;
/10
=
ХI
Х
2
Х
З
Х
4
Х
б
;
/11
=
ХI
Х
2
Х
З
Х4
Х
S
;
/12
=
ХI
Х
2
Х
ЗХ4
Х
S;
рз
=
Х
IХ2ХЗХ~Х5;
/14
=
Х
IХ
2ХЗХ4ХS
;
ро
=
Х
IХ2
Х
З
Х
4
Х
S;
Гл.
11.
КлаССUфUl>ацuu
116 =
Х
1Х2ХЗ
Х
4
Х
5;
р9
=
Хt
Х
2
Х
З
Х
4
Х
5;
122 =
Х
1
Х
2
Х
З
Х
4
Х
5;
117 =
Х
1Х ZХ
ЗХ4Х5;
120
=
Х1Х2ХЗХ4Х5;
f2З
=
Х
1
Х
2
Х
З
Х
4
Х
5'
118 =
Х
1Х2
Х
ЗХ4
Х
6;
р1
=
Х
1Х2ХЗ
Х
4Х5;
р4
=
Х
1
Х
2
Х
З
Х
4
Х
5;
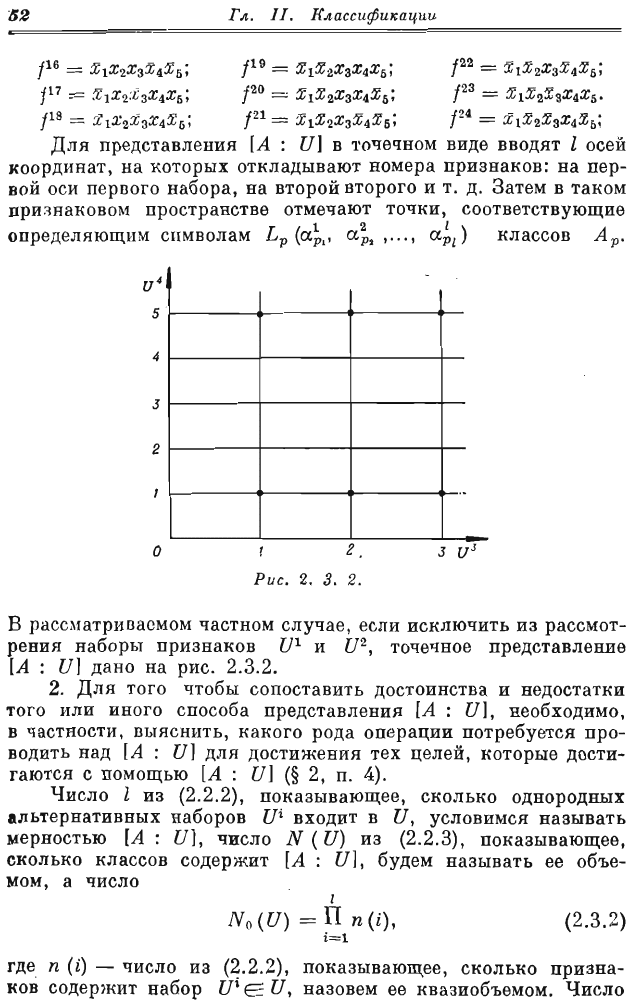
ДЛЯ
представления
[А
:
и)
в
'l'очечном
виде
вводят
l
осей
J(оор
динат,
на
которых
откладывают
номера
признаков:
на
пер
вой
оси
первого
набора,
на второй
второго
и
т.
д.
3!lTeM
в
таком
при
з
наковом
пространстве
отмечают
точки,
соответствующие
опр
еделяющим
символам
L
p
(a~"
а;,
, ... ,
a~l)
классов
Ар.
5
I----+----+----+_
4!-----f-----+----г--
Jf------+----t-----t-
2
1----+----+----;--
о
z
Рис.
2.
3.
2.
в
рассматриваемом
частном
случае,
если
исключить
из рассмот
рения
наборы
признаков
Ul
и
и2,
точечное
представление
[А
:
и)
дано
на
рис.
2.3.2.
2.
Для
того
чтобы
сопоставить
достоинства
и
недостатки
того
или
иного
способа
представления
[
А
:
и),
необходимо,
в
частности,
выяснить,
какого
рода
операции
потребуется
про
водить
над
[А
:
и)
для
достиж
е
ния
тех целей,
которые
дости
гаются
с
помощью
[А
:
и)
(§
2,
п.
4).
Число
l
из
(2.2.2),
показывающее,
сколько
однородных
альт
ернативных
наборов
Ui
входит
в
и,
условимся
называть
мерностью
[А:
и),
число
N
(И)
из
(2.2.3),
показывающее,
сколько
классов
содержит
[А
:
и),
будем
называть
ее
объе-
мом,
а
число
1
N o(U) =
П
n(i),
i=1
(2.3.2)
где
n (i) -
число
из
(2.2.2),
показывающее,
сколько
призна
ков
содержит
набор
и
;
Е
и,
назовем
ее
кваэиобъемом.
Число

§ 3.
Способы
nредсmав.ленuя
1>JtассuфuкацuЙ-nеречuсл.енuЙ
53
N°
(И)
показ~вает,
сколько
классов
содержала
бы
[А:
И],
если
бы
все
U'
Е
И
были
независимы
между
собой
на
множе
стве
А,
ИiоиilА
(§
1,
п.
6).
Выражение
6
(И/А)
= N
o
1
(U)
[N
o
(И)
- N
(И)]
(2.3.3)
назовем
показателем
связности
системы
при
знаков
И
на
мно
жестве А.
Так
как
2
-<
N
(И)
-<
N
n
(И),
то
0
-<
()
(И/А)
<
-<
(1
-
2/
No
(И)).
Очевидно,
что
чем
больше
6,
тем
больше
свя-
зей
существу
.
ет
между
признаками
И~
Е
И
i
И
между
наборами
признаков
И'
Е
И15
)
.
Установим
логические
отношения
следования
и
эквивалент
ности
на
[А
:
И].
Будем
говорить,
что
[
А:
И
i
]
следует
за
[А
:
И
j
J,
заnИ
4
сывая
[А:
И
j
]
=ф
[А
:
И
i
],
если
из
а'
(И
j
)а"
вытекает,
что
а'
(
И;)
а"
для
всех
а',
а"
Е
А.
Иначе
говоря,
если
любые
два
объекта
а'
и
а"
множества
А
неразличимы
по
системе
призна
ков
И
j
,
то
они
должны
быть
неразличимы
и по
системе
призна
ков
И
i
(§
2,
п.
2).
Отметим
два
частных
случая,
когда
имеет
место
такое
сле
дование:
1)
если
И
i
С
И
j
И
2)
если
для
каждого
набора
И
:
Е
И
j
найдется
такой
набор
И~
Е
И
j
,
что И~
=ф
Щ
(§
1,
п.
6)
.
Будем
говорить,
что
[А:
И
i
]
и
[А:
И
j
]
эквивалентны,
записывая
[А:
И
i
]
--
[А
:
И
j
],
если
[А:
И
;
]
=Ф
[А
:
ИjJ
и
[А
:
ИjJ
=ф
[А
:
И;!.
Можно
убедиться,
что
если
[А
:
И
j
)
=ф
[А
:
ИiJ,
то
раз
биение
(2.2.3)
для
И
=
И
j
детерминированно
диагнозирует
разбиение
(2.2.3)
для
И
=
И
i
(§
2,
п.
3).
Если
[
А
:
ИjJ
.......
~
[А
:
ИiJ,
1'0
они
детерминированно
эквивалентны
(§
2,
п.
3);
(2.2.3)
для
И
=
И
j
детерминированно
диагнозирует
(2.2.3):
для
И
=
И
;
,
и
наоборот:
(2.2.3)
для
И
=
И
i
дете
рминирован
но
диагнозирует
(2.2.3)
для
И
= И
j
•
Отсюда
вытекает,
что
[А
:
И
j
]
и
[А
:
И
i
],
в
таком
случае,
дают
одно
и
то
же
раз
биение
(2.2.3).
Необходи
мое,
но
недостаточное
условие
для
того,
чтобы
имело
место
[А
:
И
j
]
=ф
[А:
U
i
],
можно
записать
так:
N (
И
j
);>
;>
N
(И
i
),
а
достаточное
условие
можно
записать
в
виде
N
(И)
= N
(И
j
),
где
И
=
И
j
U
И
i
•
Будем
называть
И
i
сужением
И
по
наборам,
если
И
i
мо
жет
быть
получена
из
И
исключением
некоторых
ИВ
Е
И.
15)
Для
(2.3.1)
имеем
1
==
4, N
(И)
= 24, N
o
(И)
= 60, {j = 0,6 .

Гл.
/
/.
КлассuфU1.ацuu
НаЗ0вем
И
j
сужением
И
по
признакам,
если
И
j
может
быть
получена
и
'
3
И
исключением
И3
некоторых
наборов
и/
Е
И
некоторых
ПРИ3НaI{ОВ
ui,
Е
И/,
без
нарушения
альтернатив
ности
И/.
Естественно,
что
можно
говорить
и
о
И/О
которая
является
сужением
И
и
по
наборам
и
по
признакам
16
) •
При
переходе
от
[А
:
И]
к
[А
:
И
i
],
[А:
И
j
]
и
[А
:
И
k
)
условимся
говорить
о
сужении
[А
:
ИI
соответственно
по
мер
ности,
масштабам
и
размерам.
m
Представим
И
в
виде
И
= U
И
j
,
условимся
называть
И
j
З=1
компонентами
И.
При
переходе
от
[А:
И)
к
[А:
И
j ),
j =
= 1,2, ... ,
т,
будем
говорить
о
разложении
[А
:
И) на
состав
ляющие
[А
:
И
j
).
/
В
частном
слуtIaе,
если
И
= U
И
i
,
будем
говорить
о
раз
i=
1
ложении
[А
:
И] на
простейши
е
[А
:
И
i
).
В
случае,
если
Ир
О
И
q
I
А,
р,
q = 1,2, ... ,
т,
будем
гово
рить
о
разложении
[А:
И] на
неаависимые
составляющие
[А
:
ИJ
17
) .
Условимся
U
С
и
называть
собственной
подсистемой
И
на
множестве
А,
если
[А
:
И]
---
[А
:
'й]
.
Будем
называть
U
МИНИII
'
lальной,
обозначая
ее
через
и,
если
для
любой
И
j
с
и,
И
j
=F
tJ,
полученноп
И3
И
аналогично
тому,
как
и
была
по-
лучена
И3 И,
имеет
место
[А
:
И
j
]
1==)
[А
:
й].
Будем
различать
uщ,
которая
получается
И3
И
только
за
счет
сужения
по
мер
ности
,
(j(2
),
которая
получается
за
счет
сужения
И
только
по
масштабу,
и
U
(
~),
l{оторая
получается
И3
И
сужением
по
раз
мерам.
Переход
от
[А
:
И]
I~
[А
:
И(lI)]
,
h = 1,2,3,
будем
назы
вать
IIlинимиза
цией
[А:
И).
Система
признаков
И
может
иметь,
вообще
говоря,
не
скол
ько
различных
минимальных
собственных
подсистем
TJ~
'I
).
Если
И3
Ul'I),
i = 1,2, ... ,
k,
на
основе
неноторых
критериев
]6)
Оты
ет
им,
что
И,
опр
едел
яемая
(2.3.1),
является
сужением
СИl}темы
призпаков,
используем
о
й
в
статье
[60],
по
паб9рам.
, .
17)
Оч
е
видно,
что
Up O
Uq
I A'
если
U'
O
U'
I
A
,
U'ЕИ
р
'
И'ЕU
q
(§
1,
п.
6)
.
При
разлож
е
нии
[
А
:
И
]
на
пезависимые
составляющие
.l
l
:
И
i
m
имеет
м
ес
то
N
(И)
=
П
N
(
И
j
).
З
=
1

§
3.
Способы
nре
дсmае.л,еnuJt
КАассuфu,,ацuй-nеречuсдеnuй
55
lВыбрана
какая-либо
одна
Й~),
то
при
переходе
от
[А
ИJ
к
[А
:
И~}
J
будем
говорить
об
эффектизации
[А
:
ИJ.
"Усло
вимся
иногда
обозначать
[А
:
И(
h
)]
через
[А
:
ИJ
м
,
а
[А
:
U
~)
]
через
[А
:
UJ
э
.
Переход
от
[А
:
И]
к
{[А:
ИJ}
(§
2,
п.
3)
впредь
усло
,
вимся
называть
обобщением
[А:
UJ.
Очевидно,
что
вс
егда
имеет
место
[А:
ИJ =Ф
{
[А:
ИJ}.
Будем
называть
U(l1)
С
И
собств
енн ой
условной
18)
подсистемой
И,
если
выполнено
- (h) -
[А:
И
J
=Ф
{[А
:
ИJ}.
Назовем
И
(h)
минимальной,
обозначая
ее
через
И,
если
для
любой
И
i
С
U
(
М,
U
i
=F
U (
II)
имеет
ме
сто
[А:
ИiJ
=1=>
[А
:
UJ.
Поскольку
И
может
иметь,
вообще
говоря,
несколько
минимальных
условных
собственных
подсистем
(j
(l')
, j = 1,2,
...
...
, r,
то
можно
на
основе
некоторых
крит
ерие
в
выбрать
из
них
.эффективную
поде
ист
ему
U~).
Пусть
л
-
некоторый
автомат
[1
J,
обладающий
способно
стью
превращать
{
[А:
ИJ}*,
которое
подается
на
его
вход,
11
{[А
:
UJ}**,
которое
выдается
им
на
выходе
.
Алгоритм
11л(А),
который
позволяет
совершить
такой
же
переход
от
{[А
:
:
UJ}*
к
{[А
:
ИJ}**,
назовем
алгоритмом
подражания
авто
мату
л
на
множестве
А.
Если
им
ее т
место
{[А
:
ИJ}
*
=Ф
{[А
:
И
Н*
*,
то
f.tл(А)
и
л.
будут
называться
тривиальными.
Если
{[А:
ИJ}**
=Ф
ОА
:
:
UJ
} *,
то
f.t
л
(А)
и
л
будут
называться
нетривиальными.
Пусть
f.t
~
(А)
ест
ь
нетривиальный
алгоритм
подражания
.автомату
л
на
множестве
А.
f.t~
(А)
({[А
:
U]}~
=Ф
([А
:
U
J}~
·
).
(2.3.4)
'Очеви
дно
,
'Что
если
известна
[А
: UJ,
то
всякий
f.t
~
(А)
можно
представить
через
два
тривиальных
алгоритма
подражания
.автомату
л
на
множестве
А:
f.tl
(А)(IА
:
ИJ)
=Ф
{[А:
UJ}
~
,
f.t
~
(
А
)
([А:
И])
=Ф
([А
:
U]}~
·
.
(2.3.5)
3.
Обсудим
достоинства
и
недостатки
различных
способов
представления
[А
: UJ.
Ясно,
что
табличный,
графический
и
точечны
й
способы
обладают
наглядностью.
В
этом
их
преиму-
18)
Условной
в
том
смысле,
что
она
выбирается
для
такого
разбиен и
я
А,
о
котором
известно,
что
оно
получено
обобщ
ением
[
А
:
И].

56
ГАава
//.
КАассuфuкацuu
щество
перед
функциональным
представл
е
нием и
представле
н
ием
строчками.
Однако
точечный
способ
т
е
ряет
наглядность
·
при
l
:>
4,
а
табличный
и
графический
способы
оказываются
крайне
громоздкими
при
N
o
(
И)
:>
500.
Если
учесть
необхо
димос
т
ь
проведения
различных
операций
над
[А
:
ИJ,
о
кото
рых
речь
шла
выше,
то
можно
считать,
что
табличный,
графи
ческий
и
точечный
способы
оказываются
непри
е
млемыми
длл
l
:>
4, N
o
(
И)
:>
100.
3а
крайне
редким
и
сключ
е
ни
е
м
,
в
гео
логии приходится
иметь
дело
именно
с
такими
[А:
ИJ.
дЛЯ
которых
l
:>
4
и
N
o
:>
100.
По
этой
причин
е
для
г
е
оло
гии
подходящими
способами
представления
[А
:
И]
явля
ю
тся,
вообщ
е
говоря,
только
функциональный
и
строчечный
.
Дли
кодировки
эксперим
е
нтального
материала
пр
е
имущ
е
ство
имеют
строчки
19
),
а в
остальных
отношениях
-
бул
е
вы
функции
[61, 81].
4.
Дадим
предварительную
2О
)
формул
и
ровку
трех
основ
ных
задач
детерминированной
теории
геологич
е
ск
и
х
классифи
каций
.
Пусть
задана
[А:
ИJ
-
а-классификация-пер
е
числе-
ние
множества
А
по
системе
при
знаков
И.
Явный
вид
[А
:
ИI
дается
(2.2.3),
а
явный
вид
И
дается
(2.2.2).
(1)
В
случае
б
(И/А)
>
О,
где
б
(И
/
А}
-
пок
а
затеЛJ~
связности
V
на
А,
определя
е
мый
(2.3.3),
требу
е
тся
указать
алгоритм
для
выделения
независимых
компонент
И
j
сИ.
(2)
В
том
же
случае
б
(И
/
А)
>
о
требуется
указать
а
л
го
ритм для
перечисления
всех
U
}h
) -
минимальных
собств
е
нных
подсистем
И.
(3)
Положим,
что
задано
I
[А
: UJj -
производное
п
е
ре
числение
от
[А
:
ИJ.
Требуется
указать
.
алгоритм
для
пер
е
чис-
ления
вс
е
х
fj
~
h
)
-
минимальных
условных
собственных
под
систем
И.
Отметим
такж
е
задачу:
(4)
Определить
необходимые
и
достаточные
условия
при
надл
е
жности
а
Е
А
к
н
е
которому
наперед
заданному
классу
I[A:
ИJ}.
5.
Дадим
кратк
ие
содержательные
г е
ологич
е
ские
поя
с
не
ния
к
операциям
над
[А
:
И] и
основным
зад
ачам,
сформули
рованным
в
п.
4.
19)
Строчки
для
удобства
можно
записывать
н
а
специальных
перфо
картах.
20
)
Предварительную
в
том
смыс
л
е
,
что
эта
формулировка
нужд
а
ется
в
уточнении
с
точки
зрения
существования
и
е
динственности
решения
этих
задач.

§ 3.
Способы
nредсm
а
меnuя
1I:л
а
ССUфU1l:ацuй-nеречuсмnuй
57
Операции
сужения
(а
также
расширения)
[А
:
и]
по
м
е
р
ности,
масштабам
и
размерам
необходимы
для
сопоставления
между
собой
[А:
U
j
],
постро
е
нных
различными
авторами,
а
Тaltже
получения
таких
[А
:
и]
,
которые
могут
быть
обрабо
таны
с
учетом
имеющегося
экспериментального
материала
и
возможностей
существующих
ЭВМ.
Операции
разложения
(а
также
сложения)
[А:
И]
на
составляющие
необходимы
для
экспериментальной
и
формаль
ной
проверки
громоздких
[А
:
и]
по
частям
и
в
целом.
В
частности,
разло
ж
ение
[А
:
И]
на
независимые
со
с
тав
ляющие
позволяет
представить
в
наглядном
виде
(табличном,
графическом
или
точечном)
такие
[А
:
и],
для
которых
l
;;>
4,
N
o
(И)
> 100.
Следует
отметить
особую важность
операции
обобщ
е
ния
[А
:
и],
понятия
о
{[А
:
и]
J.
Получение
таких
разбиений
А
связано
с
получением
обобщенных
представлений
об
А.
Можно
показать,
что
понятие
о
I
[А
:
И]}
включает
в
себя
все
пред
ставления
о
«видах», «родах»,
«сем
е
йствах»
и
т.
д.,
ROTopbl
e
нам
угодно
ввести
[101, 102, 35, 57,
58]21).
в
частном
случае
[А
:-
:
U]~.
дает
то
представление
о
(<палеонтологическом
виде»,
RO-
торое
требуется
нам
из
содержательных
геологичеСRИХ
сообра
жений
(глава
IV,
§.
1,
п.
5).
Введение
понятия
об
!1л
-
алгоритме
подражания
автома
ту
л
потребовалось
для
того,
чтобы
попытаться
наметить
более
.
общий
подход
R
алгоритмам
распознавания
[70]
применит
е
ль
но
R
нуждам
геологии
(§
6,
пп
.
9, 10).
Задача
(1)
обеспечивает
ЭRОНОМНЫЙ
подход
R
анализу
св
я
зе
й
м
е
жду
наборами
признаRОВ
U
i
с:
И
И
между
признаками
u~c:
U
i
.
Этот
анализ
сводится
R
анализу
связей
внутри
неза
висимых
Rомпонентов,
Rоторые,
RaR
правило,
связаны
с
Rачест
венно
различными
СОВОRУПНОСТЯМИ
свойств.
Например,
в
с
лу
чае
зал
е
жей
нефти
и
газа
таRи
е
Rомпоненты
могут
быть
связаны
с
фИЗИRо-химичеСRИМ
составом
угл
е
водородов,
геометри
е
й
за
лежи
и
литологией
ПОRрывающих
толщ
.
Задача
(2)
обеспечивает
получение
таRОЙ
[А
:
И],
Rоторая
оптимальным
образом
удовлетворяет
поставленным
сод
е
ржа
тельным
требованиям,
например
наиболее
распростран
е
нным
меТОДИRам
ЭRспериментов
и
наличию
наиболее
полных
и
т о ч
ных
данных,
минимуму
затрат
для
определения
прина
д
леж
ности
а
R A
i
и
др.
11)
К
сожалению,
все
существующие
сейчас
«систематизации»
опира
ются
на
н
е
формализованвые
пр
е
д
с
тавле
н
ия
о
«видах»
[57, 58, 101)
как
подразделениях,
существующих
н
е за
висимо
от
наших
целевых
установок.

.
58
r
Aal1-Q,
11
,
RАассuфu"ацuu
Задача
(3)
тесно
связана
с
построением
диагностических
,
Rлассификаций
(§
6),
в
частности так
называемых
генетических
Rлас
.
сификациЙ
22
)
,
когда
морфологически
различным
объектам
·
а
Е
А
приписывается
один
и
тот
же
механизм
образования.
:
Эта
задача
вместе
с
задачей
(4)
имеет
непосредственное
отно
:
шение,
например
.
,
к
определению
«границ
видов»,
необходимых
и
достаточных
условий
принадл
ежности
а
Е
А
к
(<виду»
А;.
§ 4.
К
ре
шению
основных
задач
цетеrМИНИfованной
теории
геологических
классификаций
1.
Рассмотрим
логическую
задачу,
решение
которой,
с
учетом
известных
результатов
[94, 95 1,
позволяет,
как
будет
показано
·
в
дальнейшем,
построить
алгоритмы
для
решения
·
задач,
сформулированных
в
§ 3,
п.
4.
2.
В
качестве
полной
системы
функций
алгебры
логики
[
33,
46,
84
1
выберем
конъюнкцию
&,
дизъюнкцию
V
и
отрица
ние
- .
Как
обычно,
в
записи
булевых
выражений
знак
конъюнк
,
ции
в
дальнейшем
будем
опускать
там,
где
это
не
вызовет
не
.
доразумениЙ.
Независимую
переменную
будем
обозначать
че
рез
Х,
через
т
-
количество
независимых
переменных
рас-
,
сматриваемой
булевой
функции.
Для
аргумента
Xj , i = 1,2, ... ,
т,
и
его
отрицания
аналогично
предыдущему
(§
3,
п.
1.)
вве-
дем
обозначение
xi
i
•
В
ai
&
сч,
& &
О·
ыражение
.
вида
Xi
I
Xi
, .
...
Х
.
t,.,
r <,
т,
где
Xi"
Xi,
,
..
. ,
Xi
l
1,
. r
попарно
различимы,
будем
называть
элементарной
конъюнк
.
циеЙ,
а
число
r -
рангом
элементарной
конъюнкции.
Со
ответ-
0"
О
'
а'
ственно
выражение
вида
Xi,"
у
'
Xi
,
"V
...
VX.'r,
r <,
т,
будем
на-
1
J
•
22)
До
сих
пор
.
не
имеется
ч
е
ткого
определения
«генетическию)
клас
СИфJlкационных
постро
е
ний.
Формально
[А
:
И] можно
сч~тать
«генети
!lеской
»
,
во-первых,
когда
хотя
бы
один
набор
признаков
И'
Е
U
связан
с
«ген
ез
исом
»
(условия,
обстанqвки,
способы
образования),
во"вторых,
~oгдa
все
наборы
признаков
·
И'
Е
U
оказываются
связанными
с
«гене
зи
сом»,
в-третьих,
когда
ни
один
набор
признаков
И'
Е
U
не
связан
'
с
«генезисом»,
но
[А
:
.
И]
=ф
[А
:
·
и*
]
,
где
И*
-
система
признаков,
свя
занная
с
«генезисом
»
.
В
первом
случае
«генезис
»
выступает
как
одно
из
средств
различения
объ
ек
тов
множеств
а
А
в
каких-то
содержательных
целях.
Во
втором
случае
«генезис»
выступает
как
цель,
проводит
с
я
пере
IШсл
е
ни
е
объектов
множ
е
ства
А
с
точки
зрения
их
«генезиса
»
.
В
тр
е
тьем
·
случ
ае
«генезис»
выступа
е
т
т
а
к
же,
как
цель,
но
такая,
которая
ДОС1игаетс
я
с
помощью
диагноза.
Напомним,
что
необходимым
условием
дет('рмини
ров
анного
диагноза
является
N
(И)
> N
(и
*).
Поэтому
всякий
детерми
.
вир
ованныЙ
гене'tический
по
дход
явля
етс
я
более
грубым,
чем
морфологи
'
.е
СКlIЙ.

§
4.
в:
решению
основных
задач
59
.зывать
элементарной
дизъюнкцией,
а
число
г-рангом
элемен
~арной
дизъюнкции.
Выражение
вида
P
1
V
P2
V
..
·.
V
Р
Н
,
где
Р
l'
Р2,
...
,
РR-эле
.ментарные
конъюнкции,
будем
называть
дизъюнктивной
нор
мальной
формой (ДНФ).
:Конъ~нкции
P
i
наЗ0вем
членами
ДНФ.
Соответственно
выражение
вида
С
1 &
С2
& ... &
С
н
,
где
·
С
1
,
С2,
... ,
С
Н
-
элементарные
дизъюнкции,
будем
называть
:RОНЪЮНКТИВНОЙ
нормальной
формой (КНФ).
Дизъюнкции
C
i
:наЗ0вем
членами
КНФ.
ДНФ
(КНФ)
наЗ0вем
совершенной
(СДНФ,
СКНФ),
если
:ранг
каждого
И3
ее
членов
будет
равен
т
-
числу
независи
мых
переменных.
ДНФ
(соответственно
КНФ),
содержащая
,
наименьшее
число
букв
X?i
по
сравнению
со
всеми
другими
ДНФ
(соответственно
КНФ),
эквивалентными
данной
Функ
.ции
[33, 46, 84],
будет
называться
минимальной
ДНФ
(соот
ветственно
:КНФ)
(МДНФ,
МКНФ).
Будем
говорить,
что
элементарная
конъюнкция
Р
1
ранга
Г
1
(Г
1
-<
т)
поглощает
элементарную
конъюнкцию
Р2
ранга
Г2
(Г2
;>
г
1
),
если
Р
1
&
Р2
=
Р2.
Аналогично
булева
функция
/1
(Х
1
,
Х
2
,
•.•
,
Х
т
)
поглощает
булеву
функцию
/2
(Х
1
,
Х2,
..•
,
Х
т
),
,
если
р
&
/2
=
/2.
Напомним,
что
элементарные
конъюнкции
Р;
.
и
P
j
назы
ваются
ортогональными,
если
Р
;
& P
j
=
о.
Для
того
чтобы
две
элементарные
конъюнкции
были
ортогональны,
необходимо
и
достаточно,
чтобы
каждая
из
них
содержала,
по
крайней
мере,
один
общий
аргумент
xi
i
,
при
этом
В
одной
И3
конъюнкций
,
Oi
=
о,
а в
другой
0i
= 1.
Аналогично
функции
р
и
j2
назы
,
ваются
ортогональными,
если
11
&
J2
=
о.
Для
того
чтобы
две
функции,
заданные
в
виде
ДНФ,
11
=
Р
1
V
Р
2
V
...
V P
kt
,
j2
=
P~
V
Р;
V
...
V
P~,
-были
ортогональны,
необходимо
и
достаточно,
чтобы
были
ор
~огональны
всевозможные
пары
конъюнкций
Р
;
иР;,
i = 1,
2,
...
, k
1
,
j = 1,2,
...
, k
2
•
Функцию
/
(Х
1
Х2,
•
.•
,
Х
т
)
называют
монотонной,
если
/
(Х
1
,
Х2,
.
•.
,
Х
m
)
-<
/
(X
1
,
Х
2
,
.
•.
,
Х'т)
,
где
Х
1
-<
Х
1
,
Х2
-<
Х2
,
..•
,
Х
т
-<
.
-<
x
,
~
,
.
Заметим,
что
всякая
формула,
записанная
через
конъюнк
.
цию
И
дизъюнкцию
(без
отрицания),
задает
некоторую
моно
тонную
функцию.
3.
Будем
обозначать
символом
F (f)
формулу,
задающую
<
булеву
функцию
1
(Х
1
,
Х2
,
.
..
,
Х
т
)·
