Fishwick P.A. (editor) Handbook of Dynamic System Modeling
Подождите немного. Документ загружается.

23-14 Handbook of Dynamic System Modeling
The initial value of Q is assumed to be zero and the initial value of R is the number of parallel servers.
Of course, there are several equivalent ERGs for this system (in fact, special cases of this system can be
simulated with only one “Finish” event vertex).
We will first “read” the ERG in Figure 23.15. As discussed earlier, ERGs are read by substituting for
A, B, (i), and t and paraphrasing the arc definition in Figure 23.4. An accurate and concise description of
the system dynamics can typically be given with only one sentence for each arc in the graph. The four arcs
of the ERG in Figure 23.15 give a four sentence full description of the system dynamics (event names are
in italics).
Jobs arrive every t
a
time units. Jobs that arrive to find an idle resource and complete a full batch
will immediately start service. A resource will finish processing a batch of jobs t
s
time units after it
starts processing. When a resource finishes a batch, if a full batch of jobs is waiting, the resource can
immediately start on the next batch.
Again, for networks of queues, the ERG represents a generic element of an array of ERGs by using event
parameters k and j in the basic arc definition.
We will start by specifying the trajectory (say, waiting times or queue sizes) of n jobs processed in
a G/G/1 FIFO queue as the solution to a linear program. The G/G/1 queue has general random time
between job arrivals, general service times, and a single server. The ERG for a G/G/1 queue is Figure 23.15
with a batch size of B =1 and the number of idle resources R initially equal to 1. For this system, the
linear program that specifies the dynamic system trajectory is almost obvious. The nonnegative decision
variables in our linear program will be the event times. Here
A
i
= the time of the ith Arrival event
S
i
= the time of the ith Start event
F
i
= the time of the ith Finish event.
The objective or the optimization will be to execute each event as soon as possible subject to the constraints
imposed by the ERG,
Min Z = (A
i
+S
i
+F
i
)
Other objective functions will work for this model. In fact, we do not need to include the job arrival times
in our objective function since they are not scheduled by conditional arcs. Also, if we knew that the N jobs
occurred in the same busy period, then the simple objective of minimizing the length of the busy period,
F
N
, would suffice.
Each of the arcs of the ERG imposes a constraint on how events can be executed. For a given input
process of arrival times and service times (t
A
(i), t
S
(i): i =1, 2, ...n). Simple linear constraints are enforced
by each arc in the ERG.
A
i+1
−A
i
= t
A
(i) (Arrival-Arrival arc)
F
i
−S
i
= t
S
(i) (Start-Finish arc)
A
i
≤ S
i
(Arrival-Start arc)
F
i
≤ S
i+1
(Finish-Start arc)
A
i
, S
i
, and F
i
≥ 0
The analytic solution to this model is the dynamic system trajectory. If, for example, we can compute
the sequence of customer waiting times as, W
i
=S
i
−A
i
either after the model is solved or by adding
it as a constraint. The queue length process Q(t) =C
A
(t) −C
S
(t) can also easily be computed from the
trajectory.
We now illustrate the details with the simulation of multiple parallel resources and batch process-
ing in Figure 23.15. A general algorithm for expressing ERGs as linear programs is given in Chan and
Modeling Causality with Event Relationship Graphs 23-15
Schruben (2005). We will use the well-known relationship between an event and its counting point process
(Nelson, 1995),
E
i
≤ t ⇔ C
E
(t) ≥ i
This relationship simply enforces the forward progression of time: if E occurs i times at or before time t
then it will have occurred at least that many times by time t.
The number of jobs in line at time t, Q(t), is equal to the number of Arrival events (incrementing Q
by 1) that have occurred minus B times the number of Start events (each decrementing Q by B) that have
occurred, or,
Q(t) = C
A
(t) −B ∗ C
S
(t)
At any time in the simulation Q(t) must be greater than zero. Consider the instant, t =S
i
, at which the ith
batch service starts, then C
S
(S
i
) =i.
Therefore,
0 ≤ Q(S
i
) = C
A
(S
i
) −B ∗C
S
(S
i
)
⇒ C
A
(S
i
) ≥ B ∗C
S
(S
i
)
⇒ C
A
(S
i
) ≥ B ∗i
⇒ A
B∗i
≤ S
i
This constraint, A
B∗i
≤S
i
simply says that, since jobs are processed B at a time, then B times as many jobs
must arrive as have started service.
Consider again any instant, t, at which the ith service can start. For service to start, there must be at
least one idle resource at time t. The number of idle resources at any time is equal to a count of the initial
number of idle resources, R, less than the count of the number of Start events (decrementing resources)
plus the count of the number of Finish events (incrementing resources). Therefore, at the time of the ith
Start event, S
I
, there must be a positive number of idle resources,
R +C
F
(S
i
) −C
S
(S
i
) ≥ 1
⇒C
F
(S
i
) ≥ C
S
(S
i
) +1 −R
⇒C
F
(S
i
) ≥ i + 1 −R
⇒F
i+1−R
≤ S
i
This constraint, F
i+1−R
≤S
i
simply says that, since there are only R resources, the number of Start events
cannot exceed the number of Finish events by more than R+1. This constraint is enforced in the simulation
by the arc from the Finish event to the Start event in the ERG of Figure 23.15.
In general, the number of occurrences of events that decrement the availability of a limited resource
can never exceed the number of events that increment that resource by the more than the number of such
resources. Sets of vertices in the resource-driven simulation that relate to limited resources will have such
constraints even if they do not share an arc in the ERG.
To summarize the ERG in Figure 23.15 translates into the following linear program:
(Events occur as soon as feasible)
Min (A
i
+S
i
+F
i
)
The two unconditional timed arcs provide the constraints
A
i+1
= A
i
+t
A
(i) and
F
k
= S
i
+t
S
(i)

23-16 Handbook of Dynamic System Modeling
While the two conditional zero-delay arcs provide the constraints
S
i
≥ A
B∗i
and S
i
≥ F
i+1−R
The subscripts on the last constraints reflect the bounds on the number of resources, R, in our system and
the Batch size.
Applications of modeling ERG trajectories as the solutions to linear programs include developing
optimal resource scheduling models, using the duals of the linear programs for sensitivity analysis, using
properties of the linear programs to prove system properties such as tandem queue reversibility, and
determining stochastic orderings of systems (Chan, 2005).
23.5 Simulation of Event Relationship Graphs
ERG models can be developed graphically and simulated easily with the software package SIGMA
(Schruben and Schruben, 2005), This software provides a simple but powerful and practical method
for ERG simulation modeling. SIGMA, the Simulation Graphical Modeling and Analysis system, is an
integrated, interactive approach to building, testing, animating, and experimenting with discrete-event
simulations. SIGMA supports the full simulation ERG model life cycle from model building and testing
to output analysis, animation, documentation, and report writing.
For speed and portability, SIGMA can automatically translate a model (with a mouse click) into a fast C
code. Not only does this code allow models to run thousands of times faster, but also the compiled models
can be run from a spreadsheet interface using preprogrammed Excel Visual Basic Templates (Schruben
and Schruben, 2005) with multiple experimental runs batched together. SIGMA also can write a verbal
description of a model in English to aid in debugging and model verification.
SIGMA graphically models the events taking place within a system and the cause and effect relationships
among these events. One of SIGMA’s more useful features is that simulation models can be created,
enriched, and edited while they are running. Events can be added, altered, executed, canceled, or deleted
during a simulation run. Logic can be changed and errors corrected without stopping a run to change
code and recompile, so the modeler can interactively “replay” interesting events.
Animation support is fundamentally different in SIGMA from most other simulation modeling envi-
ronments. Animations are not created from simulation models using separate add-on software. In SIGMA,
the animation and the simulation code is identical. In addition to graphical modeling, analysis, and anima-
tion, SIGMA also includes graphical data tracking tools and allows pictures, graphs, plots, and data to be
pasted into spreadsheets and word processors.
Multiple SIGMA sessions can be run concurrently. Objects can be copied and pasted from one modeling
session to another. In fact, models can be developed in one SIGMA session and then graphically integrated
into another simulation model while that model is executing.
23.6 Event Relationship Graph Analysis
There is a rich literature on the analysis of ERGs. This includes mappings of GSMPs and Petri nets into
ERGs as mentioned earlier allowing the rich analytical methodologies of Petri nets and GSMPs to be
applied to ERGs. There are also ERG-specific analytical tools such as in Som and Sargent (1990), where
rules for elimination and consolidation of events for more efficient simulation are given. They also identify
events that“interact” and might cause logical errors when they occur at the same time and are executed in
different orders.
Earlier it was shown that how the set of all possible sample paths from an ERG as the solutions
to optimization programs (Schruben, 2000; Chan and Schruben, 2005). This is done by algorithmic
mapping of the ERG models into linear and mixed integer programs. These programs are often simple

Modeling Causality with Event Relationship Graphs 23-17
linear programs which have duals that can be used for sensitivity analysis. For example, the dual of a
G/G/s queueing system is what is known in operations research as the production lot sizing problem.
These optimization model representations for ERGs also provide optimal resource scheduling models and
alternative simple proofs of complicated system properties, such as the reversibility of tandem queues
(Chan and Schruben, 2003a, 2003b; Chan, 2005). This mapping allows the rich algorithms and theory of
optimization to be applied to ERGs.
23.7 Experimenting with ERGs
Parametric ERGs can be used for running experiments where simultaneous replications of the same or
competing systems are done in a single run. An event parameter is used to designate to which system each
event execution belongs.
It is also possible to use different timescales for the systems corresponding to different design points. In
this manner, the run can focus on factor settings or systems that are likely to be optimal and feasible rather
than spend time simulating systems that are not contenders. This idea can be generalized as illustrated
in Hyden (2000) where a large-scale experiment to optimize a production system was solved orders of
magnitude faster than the commercial simulation optimization software available at that time.
In Schruben (1997) an example is presented using a penalty function to dilate event times to find the
cycle-time constrained capacity of a queue. The cycle-time constrained capacity of a queueing system is
defined as the maximum job arrival rate to the system so that the average job delay time is below some target.
Determining the cycle-time constrained capacity of a queueing system is straightforward when the
cycle-time function is known from queueing theory. However, small errors in approximating this function
can cause large errors in capacity estimation. This is particularly true for the short cycle-times found in
highly competitive industries; the trade-off curve in this region is flat. Standard simulation experiments are
almost useless in estimating the asymptotic upper bound on queueing system capacity. At high arrival rates,
observed cycle-times are highly correlated and run initialization bias is a serious concern. These factors
combine to give simulation estimators of heavy-traffic cycle-times both high bias and high variance. For
example, simulation of millions of wafer flows are needed to estimate semiconductor factory capacities.
An experimental strategy for simulation optimization is to assign parameters to the “arrival”from a grid
of interesting arrival rates. A range of arrival rates can then be simultaneously simulated during a single
run. This grid can be refined during the run if the initial grid is found to be too coarse.
As the simulation progresses, we want to spend more and more time running events that are near
the solution. To do this we will penalize rates that are not performing well or appear to be infeasible.
The “penalty function” takes the form of time dilation for events associated with arrival rates that are
unlikely to be near the capacity. When their relative timescales are increased, events will naturally tend to
be scheduled near the end of the pending events list. If the events list is very large, these penalized events
become essentially irrelevant and have no detrimental effect on execution speed. The number of event
executions devoted to a particular design point reflects the likelihood that the design point is optimal.
Hence, the simulation run is concentrated on those experimental points where success is most likely. This
has the positive effect of minimizing the estimator variance at exactly the right place. Events corresponding
to uninteresting parameter values will occur occasionally as in simulated annealing. This is necessary if
there is to be any theoretical hope of global optimization.
For illustration, this experimental technique was tested with a simulated single queue like that in
Figure 23.5. The simultaneous replication strategy and time dilation techniques in Schruben (1992) were
used. For this test system, exponential interarrival times and service times were used so the true cycle-time
constrained capacity rate is known. To put this problem in perspective, conventional replication methods
would require hundreds of thousands of simulated jobs to get a reasonably good estimate of the cycle-time
constrained capacity of this simple system.
Without using any of the information about the system (or even the fact that cycle-times increase
with arrival rate), we chose a grid of 40 arrival rates from 0.03125 to 1.25 is run. Therefore, there were
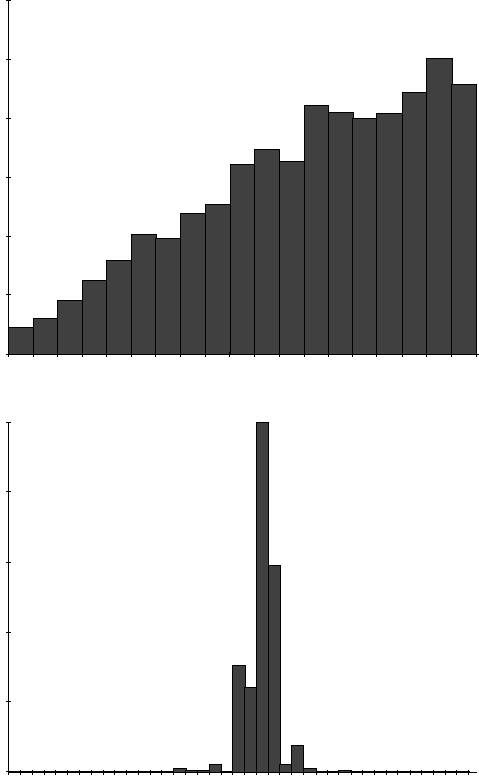
23-18 Handbook of Dynamic System Modeling
Event frequency (soln = 24, max = 30)
I
0
329
658
987
1316
1645
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Count
Event frequency without time dilation
I
0(a)
(b)
169
338
676
845
1014
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
507
Count
FIGURE 23.16 Event execution frequency. (a) Without time dilation and (b) with dilation.
40 different possible parameter values for each executed event, depending on which arrival rate spawned
the event. We will set the average processing time at 1 so systems with arrival rates over 1 are unstable. We
did not use this information so some of the systems included in our run are unstable.
Let W
i
denote the current average job delay corresponding to the ith arrival rate being used. We will
estimate the W
i
< 4 capacity of this system with one simulation run. For time dilation, the timescale for
the arrival event at rate i was multiplied by (W
i
−4)
2
.TheW
i
< 4 capacity corresponds to event parameter
i =24. All event indices over 30 correspond to unstable arrival rates.
After an initialization period of 5,000 jobs, the relative frequency that events corresponding to the
different arrival rates appear in Figure 23.16(a).
For the next 5,000 jobs, a quadratic time dilation penalty was then invoked (Figure 23.16[b]). After
a total of 10,000 simulated jobs shared across all 40 systems, the event index at the correct solution of
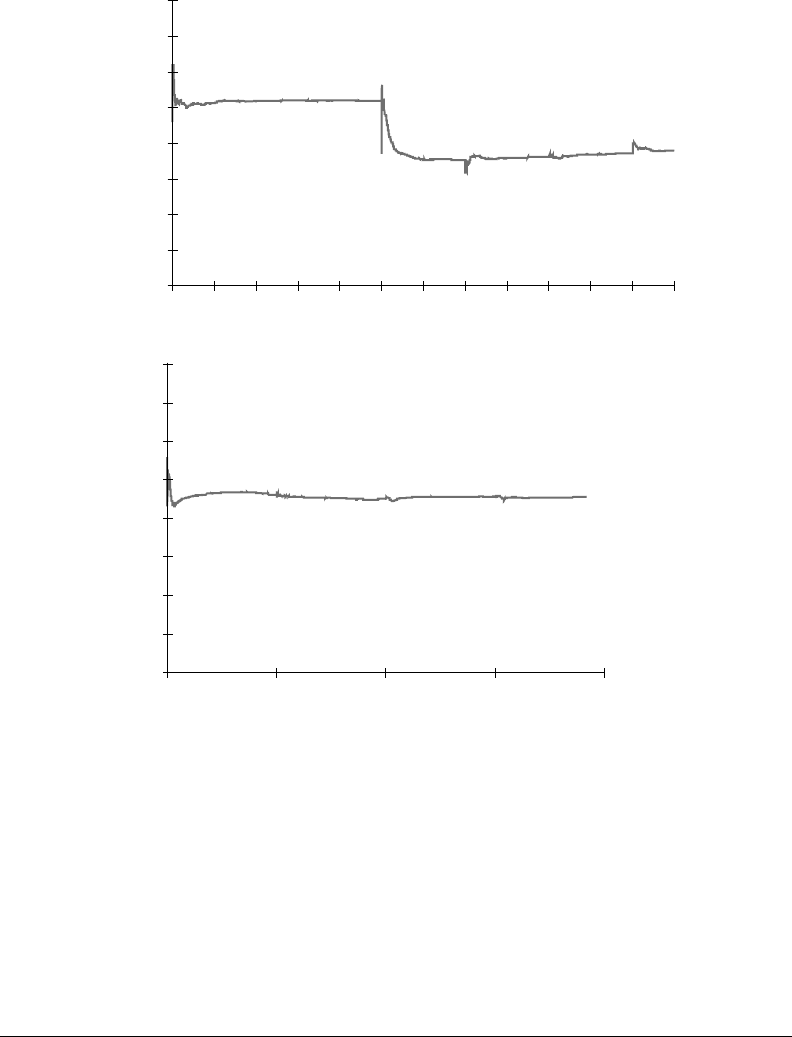
Modeling Causality with Event Relationship Graphs 23-19
Average event index (opt. = 20, max. = 30)
TOTAL
0
5
10
15
20
25
30
35
40
0
(a)
(b)
1000 2000 3000 4000 5000 6000 7000 8000 9000 1000011000 12000
AVI
0
5
10
15
20
25
30
35
40
10000 15000 20000 25000 30000
AVI
TOTAL
Average event index (soln. = 24, max = 30)
FIGURE 23.17 Average event indices for (a) W
i
< 2 and (b) W
i
< 4 capacity experiments.
24 is clearly indicated. Events with unstable arrival rates received early penalties, effectively excluding them
from the experiment.
In Figure 23.17(a) and Figure 23.17(b), average event indices are plotted for both the W
i
< 2 and W
i
< 4
capacities. Periodically, these averages are reset causing a jump in the figures. These averages quickly
converged to the correct indices for ERGs having the optimal arrival rates as their event parameters.
Summary
This chapter introduces ERGs and illustrates some of their applications and properties. ERGs are a mini-
malist approach to modeling discrete-event system dynamics that are completely general (having the full
powerof Turing machines). ERGs express the logical and temporal relationships between changes in system
state, analogous to systems of differential equations for modeling continuous state system dynamics. Para-
metric ERGs can model huge and complex systems using very small finite graphs. Specification of the initial
and terminating states for an ERG completely and unambiguously (perhaps using arc priorities) determine

23-20 Handbook of Dynamic System Modeling
the state trajectory for a discrete-event model. Such models can be easily and efficiently simulated using
software such as SIGMA.
Some analytical properties of ERGs are also presented, most notably their representation as linear pro-
gramming or mixed integer optimization models. These linear program (LP) representations allow the
rich set of analytical and algorithmic methodologies from optimization to be applied to the study of
discrete-event dynamic systems as well as define explicit dual for discrete-event systems.
Acknowledgments
The author appreciates the support of the National Science Foundation through grant DMI0323765 to the
University of California, Berkeley. He is also grateful for the contributions of his students and colleagues,
in particular, those of former students W. K. Chan, P. Hyden, M. Oman, D. Pederson, V. Peterson, and
T. Roeder.
References
Askin, R. G. and C. R. Standridge (1993). Modeling and Analysis of Manufacturing Systems,Newyork:
Wiley.
Buss, A. H. and P. J. Sanchez (2002). Modeling very large scale systems: Building complex models
with LEGOs (listener event graph objects). Proceedings of the 2002 Winter Simulation Conference,
pp. 732–737.
Chan, W. K. (2005). Mathematical programming models for discrete event systems dynamics PhD thesis,
Department of Industrial Engineering and Operations Research, University of California, Berkeley.
Chan, W. K. and L. W. Schruben (2003a). Properties of discrete event systems from their mathematical
programming representations. Proceedings of the 2003 Winter Simulation Conference, pp. 496–502.
Chan, W. K. and L. W. Schruben (2003b). Reversibility of tandem queueing networks from their
mathematical programming representations. Technical Report, University of California-Berkeley,
Berkeley, CA.
Chan, W. K. and L. W. Schruben (2004). Generating scheduling constraints for discrete event dynamic
systems. Proceedings of the 2004 Winter Simulation Conference Proceedings, pp. 568–574.
Chan, W. K. and L. W. Schruben (2005). Optimization representations of discrete-event system dynamics,
unpublished manuscript (submitted for publication).
Ding, S. and J. Yi (2004). An event relationship graph based simulation and analysis of multi-cluster tools.
Proceedings of the 2004 Winter Simulation Conference Proceedings, pp. 1915–1920.
Fishwick, P. (1995) Simulation Model Design and Execution: Building Digital Worlds, Englewood Cliffs, NJ:
Prentice-Hall.
Freimer, M. and L. W. Schruben (2001). Graphical representation of IPA estimation. Proceedings of the
2001 Winter Simulation Conference, pp. 422–427.
Hoover, S. and R. Perry (1990). Simulation: A Problem Solving Approach, Reading, MA: Addison-Wesley.
Hyden, P. (2000). Designing simultaneous simulation experiments, PhD thesis, Department of Operations
Research and Industrial Engineering, Cornell University.
Hyden, P., L. W. Schruben and T. K. Roeder (2001). Resource graphs for modeling large-scale, highly
congested systems. Proceeding of the 2001 Winter Simulation Conference, pp. 523–529.
Ingalls, R. G., D. J. Morrice, and A. B. Whinston (2000). The implementation of temporal intervals in
qualitative simulation graphs. ACM Transactions on Modeling and Computer Simulation (TOMACS)
10(3), pp. 215–240.
Law, A. and W. D. Kelton (2000). Simulation Modeling and Analysis (3rd ed.), New York: McGraw-Hill.
Nehme, D. A. and N. G. Pierce (1994). Evaluating the throughput of cluster tools using event-graph
simulations. IEEE/SEMI 1994 Advanced Semiconductor Manufacturing Conference and Workshop.
Theme—Manufacturing Excellence: A Global Challenge. ASMC’94 Proceedings, pp.189–192
Modeling Causality with Event Relationship Graphs 23-21
Nelson, B. (1995). Simulation and Stochastic Processes, New York: Wiley.
Pederson, D. and C. Trout (2002) Demonstrated benefits of cluster tool simulation. Proceedings of the 2002
International Conference on Modeling and Analysis of Semiconductor Manufacturing, pp. 84–89.
Pegden, C. D. (1986). Introduction to SIMAN (2nd ed.), State College, PA: Systems Modeling Corp.
Perkinson, T. L., P. K. McLarty, R. S. Gyurcsik, and R. K. Cavin III (1994). Single-wafer cluster tool
performance: An analysis of throughput. IEEE Transactions on Semiconductor Manufacturing 7(3),
pp. 369–373.
Sargent, R. G. (1988). Event graph modeling for simulation with an application to flexible manufacturing
systems. Management Science 24(10), pp. 1231–1351.
Savage, E. L., L. W. Schruben and E. Yucesan (2005). On the generality of event relationship graph models.
INFORMS Journal on Computing 17(1), pp. 3–9.
Schruben, L. (1983). Simulation modeling with event graphs. Communications of the Association of
Computing Machinery 26(11), pp. 957–963.
Schruben, L. and E. Savage (1996). Visualizing generalized semi-Markov processes. Proceedings of the 1996
Winter Simulation Conference, Orlando, FL, December 11–14, 1994, pp. 560–565.
Schruben, L. W. (1997). Simulation optimization using simultaneous replications and event time dilation.
Proceedings of the 1997 Winter Simulation Conference, pp. 177–180.
Schruben, L. W. (2000). Mathematical programming models of discrete event system dynamics. 2000
Winter Simulation Conference Proceedings, vol. 1, pp. 381–385.
Schruben, L. W. and T. M. Roeder (2003). Fast simulations of large-scale highly-congested systems.
Simulation: Transactions of the Society for Modeling and Simulation International 79(3), pp. 1–11.
Schruben, D. and L. W. Schruben (2005). Graphical Simulation Modeling Using SIGMA, Custom
Simulations, www.customsimulations.com.
Schruben, L. W. and E. Yucesan (1994). Transforming Petri nets into event graph models. Proceedings of
the 1994 Winter Simulation Conference, Orlando, FL, December 11–14, 1994, pp. 560–565.
Seila, A. F., V. Ceric, and P. Tadikamalla (2003). Applied Simulation Modeling, Belmont, CA: Thomson.
Som, T. K. and R. G. Sargent (1990). A formal development of event relationship graphs as an aid to
structured and efficient simulation programs. ORSA Journal on Computing 1(2), pp. 107–125.
Wu, J.-H. and C.-N. Chung (1991). Timed finite automata as the theoretical foundation for simulation
modeling with event relationship graphs. Technical Report, Department of Dec. Sci. and Inf. Sys.,
University of Kentucky, Lexington, KY.
Yucesan, E. and L. W. Schruben (1992). Structural and behavioral equivalence of simulation models. ACM
Transactions on Modeling and Computer Simulation 2(1), pp. 82–103.

24
Petri Nets for Dynamic
Event-Driven System
Modeling
Jiacun Wang
Monmouth University
24.1 Introduction ................................................................ 24-1
24.2 Petri Net Definition .................................................... 24-1
24.3 Transition Firing ......................................................... 24-3
24.4 Modeling Power .......................................................... 24-4
24.5 Petri Net Properties ..................................................... 24-5
Reachability
•
Safeness
•
Liveness
24.6 Analysis of Petri Nets .................................................. 24-7
Reachability Analysis
•
Incidence Matrix and State
Equation
•
Invariant Analysis
•
Simulation
24.7 Colored Petri Nets ....................................................... 24-10
24.8 Timed Petri Nets ......................................................... 24-12
Deterministic Timed Petri Nets
•
Stochastic
Timed Petri Nets
24.9 Concluding Remark .................................................... 24-16
24.1 Introduction
Petri nets were introduced in 1962 by Dr. Carl Adam Petri (Petri, 1962). Petri nets are a powerful modeling
formalism in computer science, system engineering, and many other disciplines. Petri nets combine a
well-defined mathematical theory with a graphical representation of the dynamic behavior of systems.
The theoretical aspect of Petri nets allows precise modeling and analysis of system behavior, while the
graphical representation of Petri nets enables visualization of the modeled system state changes. This
combination is the main reason for the great success of Petri nets. Consequently, Petri nets have been used
to model various kinds of dynamic event-drivensystems such as computer networks (Ajmone Marsan et al.,
1986), communication systems (Merlin and Farber, 1976), manufacturing plants (Venkatesh et al., 1994;
Zhou and DiCesare, 1989; Desrochers and Ai-Jaar, 1995), command and control systems (Andreadakis
and Levis, 1988; Wang et al., 2000), real-time computing systems (Mandrioli et al., 1996; Tsai et al.,
1995), logistic networks (van Landeghem and Bobeanu, 2002), and workflows (van der Aalst and van Hee,
2000; Lin et al., 2002) to mention only a few important examples. This wide spectrum of applications is
accompanied by wide spectrum different aspects, which have been considered in the research on Petri nets.
24.2 Petri Net Definition
A Petri net is a particular kind of bipartite directed graphs populated by four types of objects. These objects
are places, transitions, directed arcs, and tokens. Directed arcs connect places to transitions or transitions to
places. In its simplest form, a Petri net can be represented by a transition together with an input place and
24-1
