Fishwick P.A. (editor) Handbook of Dynamic System Modeling
Подождите немного. Документ загружается.

23-4 Handbook of Dynamic System Modeling
Cancel events
Execute event
Remove event
from list
State
Event list
Change state
Schedule events
Summary statistics
Stop Yes
No
Initialize
Advance clock to
time of next event
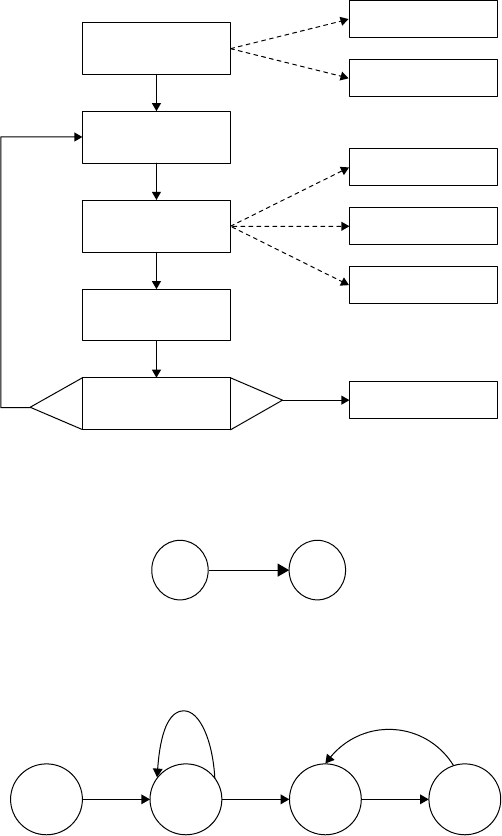
FIGURE 23.1 Main discrete-event execution algorithm.
AB
FIGURE 23.2 Event relationship: Event A might cause event B to occur, perhaps in the future.
ENTER LEAVESTART
{Idle⫹1, Busy⫽0,
Server⫽Idle}
{Queue⫽Queue⫹1} {Server⫽Busy,
Queue⫽Queue⫺1}
{Server⫽Idle}
RUN
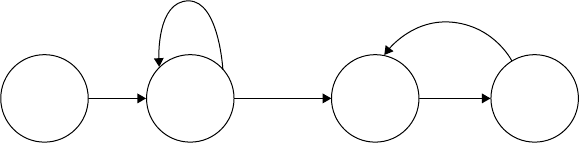
FIGURE 23.3 Event relationship graph for a single server queue.
modeling the scheduling and canceling causal relationships between pairs of events that may change the
state of a system entity. Limiting the interpretation of ERGs to flow processes can lead to errors or model
inefficiencies. ERGs are related to state machines or state transition diagrams much like a derivative is
related to a function. In a state machine or transition diagram, each node represents the value of a state;
in an ERG, each node represents a change in state.
Using this notation, we can build a model that simulates a simple waiting line with one server (e.g.,
a ticket booth at a theater and the drive-in window at a fast-food restaurant). An ERG for this system is
represented in Figure 23.3.
We will begin our examination of this graph by discussing each node. The RUN node models the
initialization of the simulation, the ENTER node models the event when a new job enters the system, the
Modeling Causality with Event Relationship Graphs 23-5
START node models the start of service event, and the LEAVE node models the end of service when a job
will leave the system. The state variables chosen to describe this system are
SERVER = the status of the server (busy, idle), initially set idle
QUEUE = the number of jobs waiting in line, initially set equal to zero
To make our model more readable, we also define the constants IDLE=1 and BUSY=0.
Next, we will focus on the changes in the state variables shown in braces. The simulation RUN is started
by making the server available for use {IDLE=1, BUSY=0, SERVER=IDLE}. (Instead of using an initial
event, the initially scheduled events are indicated by a broken arrows in the ERGs in Law and Kelton [2000].)
Each time a job ENTERs the line, the length of the waiting line is incremented {QUEUE=QUEUE+1}.
When service STARTs, the server is made busy {SERVER=BUSY} and the length of the line is decremented
{QUEUE=QUEUE−1}. Whenever a job has been finished and LEAVEs the system, and the server is again
made available {SERVER=IDLE} to serve other jobs.
The dynamics of an ERG model are captured in the arcs of the graph. We read an ERG simply by
describing the arcs exiting each node (out-arcs). In-arcs take care of themselves. Continuing with our
example, we look at each arc in Figure 23.3 (event names are in italics).
The simulation run is started by having the first job enter the system (arc from run to enter). If the
entering job finds the server idle, service will start immediately (arc from enter to start). Each time a
job enters the system, the next job will be scheduled to enter sometime in the future (arc from enter
to enter). The start service event will always schedule a job to LEAVE after that job has been served
(arc from start to leave). Finally, if there are jobs waiting in line when a job leaves, the server will start
servicing the next job right away (arc from leave to start).
The self-scheduling arc (the loop) on the ENTER event is the conventional way of perpetuating successive
customer arrivals to the system. There will typically be some random time delay between customer arrivals.
The state changes for an event node for a queueing system are typically very simple. Most of the action
occurs on the arcs of the graph. The conditions and delays associated with the arcs of the ERG are very
important; it is on the graph arcs that the logical flow and dynamic behavior of the model are defined. For
each arc in the graph we will need to define under what conditions and after how long one event might
schedule another event to occur.
To make the event relationships explicit, we label each arc with the conditions that must be true for an
event to be scheduled. Also associated with each arc will be a label that is the delay time equal to the inter-
val until the scheduled event occurs. Time will be measured in minutes for our examples. In Figure 23.4,
the basic ERG is enriched to include arc conditions and arc delay times using the notation of Askin and
Standridge (1993).
This arc is interpreted as follows: if and only if condition (i) is true right after event A occurs, then event B
will be scheduled to occur t minutes later. If the condition is not true, nothing will happen, and the arc can be
ignored until the next time event A occurs. Arcs are stochastic: an arc does not exist unless its condition is
true. If the condition for an arc is always true, the condition label is left off the graph. We will call arcs with
conditionsthat are alwaystrue unconditional arcs. Zerotime delaysfor arcs are also not labeled on the graph.
Our queueing system model with arc conditions and delay times is shown in Figure 23.5.
The state variables SERVER and QUEUE are now denoted by R and Q, respectively, and the status of S
is indicated by 1 or 0 (1 if the server is idle and 0 if busy ). In addition, the time between successive job
arrivals (often random) is denoted by t
a
and the service time required to process a job is denoted by t
s
.
BA
t
/
(i)
FIGURE 23.4 Event relationship arc with condition (i) and delay t.
23-6 Handbook of Dynamic System Modeling
{R⫽R⫺1, Q⫽Q⫺1}{R⫽1} {Q⫽Q⫹1} {R⫽R⫹1}
(R⬎0)
t
a
/
(Q ⬎0)
/
ENTER LEAVESTART
RUN
(Q)
FIGURE 23.5 Event relationship graph for a single server queue.
t
a
t
s
/
/
Customers
ENTER
system
Initialize
the RUN
(Is server
idle?)
Customer
STARTs
service
Customer
LEAVEs
system
(Are customers waiting?)
FIGURE 23.6 Verbal event relationship graph for a single server queue.
When values of t
a
are actually needed, they might be obtained from a data file or generated by random
variable generation algorithms. The graph in Figure 23.5 represents a well-defined dynamic model. To
simulate this model, only the starting and ending boundary conditions for the run need to be specified.
23.2.4 Verbal Event Graphs
Before designing a simulation model, it is important to first develop a verbal description of the system
dynamics. This can be done using a verbal ERG. This description would include state changes associated
with each node along with a verbal description of each arc condition and delay time on the graph. A verbal
ERG for a generic single server queueing system is shown in Figure 23.6.
Developing a verbal description of a system is a reasonable first step toward building a realistic and
accurate simulation model. It will help to conceptualize the major components in the system, determine
the key events and their interrelationships, and identify the state variables, arc conditions, and time delays
necessary for the model. It is easy to determine if a variable is required to define the state of a system: the
state variables needed for an ERG are those that permit testing all arc conditions in a verbal ERG. Once a
detailed verbal description has been developed, an ERG model is easier to build.
The visual modeling power of ERGs is most appreciated after one recognizes the complicated details
involved in a discrete-event simulation. The fundamental concept in ERG modeling is to use a directed
graph as a picture of the relationships among the elements in sets of expressions characterizing the dynamics
of the system. Each node of the graph is identified with a set of expressions for the state changes that
result when the corresponding event occurs. Each arc in the graph identifies sets of logical and temporal
relationships between a pair of events.
23.2.5 Reading Event Relationship Graphs
A concise description of the dynamics of an ERG model can be obtained by paraphrasing the arc definitions
given for Figure 23.4. The description will have roughly one sentence per arc. As you read the following
description, identify a single arc in Figure 23.5 with each sentence, again event names are in italics.
At the start of the simulation run, the first job will enter the system. Successive jobs enter the system
every t
a
minutes. If entering jobs find that the server is available (S>0), they can start service. Once
jobs start service, t
s
minutes later they can leave. Whenever a job leaves, if the queue is not empty
(Q>0), the server will start with the next job.

Modeling Causality with Event Relationship Graphs 23-7
Now reread the above paragraph without looking at Figure 23.5. You will see that it is a concise
description of the dynamic behavior of this queueing system. A verbal system description can be read
easily from the arcs of very complicated ERGs. Simply define each arc in the graph in a sentence—the
graph itself will connect these sentences into a complete description of the system’s dynamics. This is
an excellent way to communicate the essential features of a simulation model and a good step in model
validation. With experience in reading ERGs, it becomes easier to detect modeling errors.
23.3 Enrichments to Event Relations Graphs
23.3.1 Parametric Event Relationship Graphs
One of the most powerful enrichments of ERGs is parameters for the event nodes. Using event parameters,
a basic ERG can become an element in a multiple-dimensional array of ERGs without increasing the size
or complexity of the graph. For modeling large-scale systems, such as huge networks of queues, the ERG
represents a generic element in an array of ERGs for each component of the system. The events in the ERG
are parameterized (subscripted) with the particular station in the queueing network to which it applies by
using event parameters. For this, the basic definition of an ERG is expanded to allow the values of a string
of expressions computed after an event is executed to be passed to a string of state variables when an event
is scheduled. The values of expressions are included in boxes on the arcs.
To be explicit: define a string of state variables for each event, these are actually arguments for the
state change method for an event object. The values of these parameters are computed by a string of arc
expressions called arc attributes. The definition of a parametric arc in a simulation ERG is in Figure 23.7.
This arc is read as follows: Immediately after executing the state change for Event A, the elements of an
array of expressions, k, are evaluated. Before B is executed, the array of state variables, j, are assigned the
values previously computed for k. The arc condition and delay time, if any, are defined as before. This uses
a “pass-by-value” argument passing convention like in the C and Java programming languages.
Treating event parameters as subscripts, the graph becomes an element in an array of ERGs that model
a network composed of a large number of similar systems (Chan and Schruben, 2005). For example,
Figure 23.8 is an ERG for m parallel server queues in tandem. (The state changes are omitted in Figure 23.8
since these merely increment and decrement state variables Q(k) and R(k) for station k in the obvious
fashions.) The only change to the graph structure to obtain Figure 23.8 from Figure 23.5 is an additional
arc from the Finish(k) event for station k to the Arrival(k) event for the next station, k+1 (and the arc
attributes).
The ERG in Figure 23.8 can be easily extended to model more general queueing network systems. For
example, a generic queueing network can be modeled by adding a parameter, j, to the objects in the graph
that indicates job type. The attribute, k+1, on arc from Finish(k, j) toArrival(k, j) in the resulting ERG can
be replaced by a general routing function. Transportation resources and move times could be added using
conditions and delays on this arc. The ERG then becomes an element of a two-dimensional array (kth
station by jth job type) of ERGs. See Schruben and Schruben (2005) where a general queueing network of
arbitrary size is modeled with an ERG having only two nodes.
We conclude this section with an example of an ERG for a more complex system. This is a model of a tool
commonlyfound in semiconductor manufacturing called a cluster tool (a configuration of isolated process-
ing chambers served by one or more dedicated robots). In recent years, the use of cluster tools in semicon-
ductor manufacturing has increased rapidly, causing the performance of cluster tools to become more and
more important (see Perkinson et al., 1994; Chan and Schruben, 2004; Ding and Yi, 2004). The ERG for this
system is given by Figure 23.9, which is an element in an array of ERGs each of which defines the relation-
ships among events that simulate wafer j as it is processed or moved between chambers m and n byarobot.
Chamber 0 is a load lock for loading or removing wafers from the cluster tool. In Figure 23.9, f is the
next wafer on the robot’s move schedule; x(j) the current location of wafer j, y(j) its next destination,
and z the current location of the robot. The time for the robot to move from chamber n to chamber m is
denoted as t
n,m
and the time for chamber n to process wafer j is p
j,n.
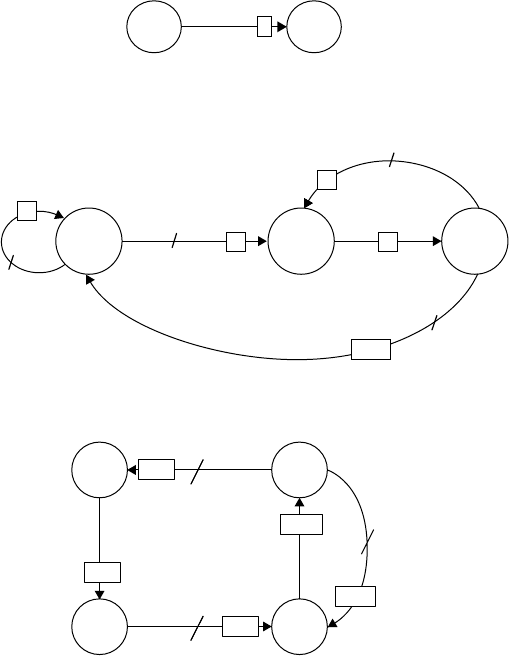
23-8 Handbook of Dynamic System Modeling
A
B
(j)
k
FIGURE 23.7 Parametric event relationship graph arc.
a
k
s
k
k⫹1
(k⫽⫽1)
(k⬍m)
(R⬎1 & Q⬎1)
(R⬎1 & Q⬎1)
Arrive
(k)
Start
(k)
Finish
(k)
kk
k
1
FIGURE 23.8 Asystemofm multiple-server tandem queues.
Start
(j, n)
PUT
(j, n)
(ii)
End
(j, n)
GET
(j, m)
t
z,n
(iii)
t
m,n
p
j,n
t
n,x(f)
(i)
j, n
j, y(j)
f, x(f)
j, n
j, n
FIGURE 23.9 An ERG model for a semiconductor cluster tool.
In the ERG of Figure 23.9, wafers move from chamber to chamber around the center rectangle in the
graph and the robot cycles between the GET and the PUT events. The events are defined as follows:
Start (j, n) =Start processing wafer j in module n; End(j, n) =End processing wafer j in module n;Get
(j, n) =Robot gets wafer j from module n and Put (j, n) =Robot loads wafer j into module n.The
relationships between these events are defined by their delay times and their arc conditions. Condition (i)
is true if there is a wafer (f ) waiting to be picked up at chamber x(f ) and the destination chamber, y(f ),
has been reserved. Condition (ii) is true when the requirements to start processing job j in chamber n are
satisfied (these might include conditions such as having a full batch for a batch process). Condition (iii)
is true if the robot is idle and has no backlog of wafers waiting to be moved. Many ERG simulations of
cluster tools have been developed (Pederson and Trout, 2002). Two of the more elegant ERGs for a generic
cluster tool, both modeled with only three events, are in Nehme and Pierce (1994) and Ding and Yi (2004).
23.3.2 Building Large and Complex Models
There is an important distinction between complicated ERG models and ERG models that are simply large.
Very large systems can merely be a large number of simple components. The ERG for such a large model
of similar components is the same as that for one of its components, but with parameter values indicating
to which components a particular event applies. Complex models, however, have different types of ERG
components, each of which might be quite complicated.
In this section, a moderately complex component is used to illustrate how ERGs can be developed and
enriched into a large system of such components. We start off using the graph in Figure 23.5 to model a
Modeling Causality with Event Relationship Graphs 23-9
RUN
(C, b, B, S)
t
a
{R⫽R⫺1;
Q⫽Q⫺max(Q;B);}
{R⫽R⫹1;}
LEAVESTART
(Q⫽b)
t
s
ENTER
{Q⫽Q⫹(Q⬍C);}
(R⬎0&&Q⫽b)
/
/
{R⫽S;}
/
FIGURE 23.10 ERG for queue with s servers, capacity c, and batch size between b and b.
system with S identical servers, a queue capacity of C, and a flexible batch size between b and B. A batch of
at least b jobs is required and at most B jobs can be processed together in a batch. The ERG for this system
is given in Figure 23.10. Boolean variables (conditional expressions that equal 1 if true and 0 if false) are
used. For example, the state change Q=Q+(Q<C) will increment Q by 1 if and only if the expression
(Q<C) is true, modeling a queue with capacity C.
Reading the arcs of this graph as before (the event node names are in italics).
A simulation run starts by setting the number of idle servers equal to S and the first job enters the
system. Jobs enter at the system every t
a
time units, but join the queue only if the Q size is less than
the capacity C. When new jobs enter, if they find an idle server and the minimum batch size of jobs
is waiting, then a batch of at most B jobs will start service. After a service time of t
b
the batch of jobs
will leave the system. When a batch of jobs leaves, if a minimum batch of b jobs is now waiting, the
server will start on the next batch of jobs.
The arc from ENTER to START is tested every time a new job enters the system regardless of whether there
is room in the queue for it to join or not. This does not cause any logical problems since the conditions
for the START event must still be satisfied.
The ERG model in Figure 23.10 can be used as the fundamental element in an array of ERGs to model
an arbitrarily large network of queues with different job types, each with a different routing among many
different server types. This is done by attaching four parameters to each event and arc in Figure 23.10 that
indicate the job type involved in an event, the step in that job’s route, the server type, and the batch size
being processed. The only structural change in the graph is a single additional arc from LEAVE to ENTER
so batches of jobs can go from one server type on their routes to the next. This arc will cause a LEAVE (job,
step, server, batch) event to schedule an ENTER (job, step, server, batch) node with attribute values given
by the expressions: job, route (job, step+1), step+1, batch. Here route(job, step) is a function that specifies
the server type for the next step on the route of a job. Complicated batching rules (jobs processed only in
batches with certain other types of jobs) can be modeled with the same graph structure; the state changes
and arc conditions can become as complex as necessary. Modeling resource failures or assembly operations
also does not require the graph structure to change (see Schruben and Schruben, 2005 for examples).
23.3.3 Variations of Event Relationship Graphs
Specializations of ERGs include resource cycle graphs (RCG) for simulating queueing networks (Hyden
et al., 2001). In an RCG, the state variables are all integer arrays and the resource state changes associ-
ated with every event are expressed as one or more integer difference equations. Simulating these models
involves increasing and decreasing the values of elements in the state arrays when specific events occur
(e.g., the number of idle servers of a particular class would decrease whenever a start_service event occurs
for this class). ERG modeling of such systems has certain advantages in terms of simplicity and efficiency in
simulation (Schruben and Schruben, 2005). For example, a simulated RCG for an actually semiconductor
factory ran orders of magnitude faster than the most popular commercial simulator (Schruben and
Roeder, 2003).

23-10 Handbook of Dynamic System Modeling
Object-oriented ERGs (called listening event graph objects, LEGOs) have been developed by Buss and
Sanchez (2002). LEGO is a public domain collection of powerful Java applets for modeling general system
objects.
Qualitative ERGs have been developed for the analysis of qualitative decisions (Ingalls, et al., 2000).
These ERGs capture the relationships between various qualitative variables, modeling uncertainty using
ranges rather than distributions and get sensitivities to various aspects of a problem. Qualitative ERGs
have been applied to project management simulations where there are many unknowns that cannot easily
be quantified.
23.4 Relationships to Other Discrete-Event System Modeling
Methods
23.4.1 Stochastic Timed Petri Nets
In Schruben and Yucesan (1994), a method for representing a general stochastic timed Petri net (STPN)
model as an ERG is presented. Basically, the nodes in a Petri net become arcs in an ERG. It has been
shown that ERGs have equivalent representations using only zero-delay conditional arcs and nonzero
delay unconditional arcs (Yucesan and Schruben, 1992; Schruben and Yucesan, 1994). These two classes of
arcs are referred to here simply as conditional and timed arcs. Timed stochastic Petri nets can be mapped
directly into ERGs by representing the transition nodes in a Petri net as timed arcs in an ERG and the place
nodes in a Petri net as conditional arcs in an ERG.
Using the method for eliminating redundant events in Som and Sargent (1990), the resulting ERG
can determine the smallest number of essential events that captures the Petri net dynamics for efficient
simulation and analysis. ERGs are more general than Petri nets, so the reverse mapping of ERGs into
STPNs is not possible without additional restrictions.
A Petri net is a directed graph with two classes of vertices, places (balls), and transitions (bars). The
graph is bipartite, meaning that no two vertices in the same class are adjacent, places are connected only
to transitions and transitions are connected only to places. The state of the system is represented by a
marking of tokens in each place. The number of tokens at a place typically represents the value of some
associated state variable.
The dynamics of the STPN are modeled by a transition firing rule. For convenience in coding a simula-
tion, we separate state transitions into two sequential operations. A transition first becomes enabled when
all of its input places are marked with at least a single token. Enabling a transition involves removing a
single token from each of its input places. Next, after a delay associated with the transition, the transition
fires, depositing a token in each of its output places. There is no restriction on the conservation of the total
number of tokens. Note that we remove tokens from input places when a transition is enabled and then
we deposit tokens when the transition fires as done in Fishwick (1995) rather than removing tokens when
a transition is fired as is more common. Removing tokens when transitions are enabled often results in a
simpler dynamic model. One can think of a token as residing in a transition while it is active. If the STPN
is simulated, the number of tokens in a transition is the number of firing “events” for this transition that
are currently scheduled to occur on the pending events list.
An STPN model for the multiple server queue is given in Figure 23.11.
In Figure 23.11, the number of idle servers is the number of tokens in place, R, and the number of jobs
in queue is the marking of the place, Q. The marking shown is the initial marking for a system with three
identical servers. The time between job arrivals is t
a
and the time for service of a job is t
s
.
Next we consider a situation where jobs are processed in a batch of size, B; this model is in Figure 23.12.
Numerous enrichments of Petri net have been suggested for modeling dynamic systems. One we will use
in Figure 23.12 is a token count which is a number placed on an arc with the number of tokens that are to
be removed on enabling a transition or deposited on firing (if different from one).
A slight modification of the system in Figure 23.12, where there is a minimum batch size, b, and
maximum batch size, B, probably cannot be represented as a general STPN where the STPN remains the
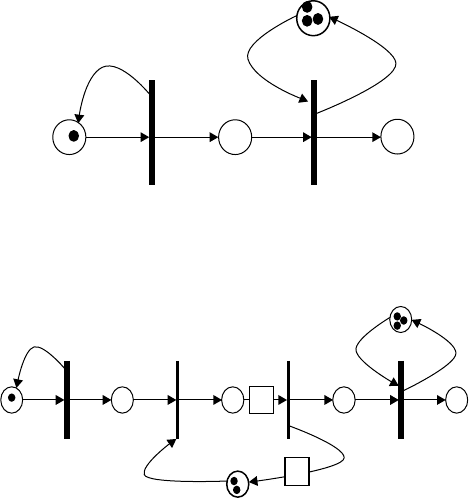
Modeling Causality with Event Relationship Graphs 23-11
t
s
t
a
R
Q
FIGURE 23.11 A multiple server queue with stochastic service times, t
s
, and job arrival times, t
a
.
t
a
t
s
R
Q
B
2
2
FIGURE 23.12 Initial marking for an STPN for a 3-server queue with batch size of 2.
same for all ranges of batch sizes with only the initial markings to differentiate the different batch size
limits. A flexible batch size such as this for arbitrary minimum and maximum batch sizes, b and B,is
modeled easily as an ERG in Figure 23.10.
STPNs provide an intuitive methodology for visualizing the dynamics of some discrete-event systems.
Using simple tokens, STPNs graphically represent the dynamic relationships between system entities,
modeling concurrency and contention for system resources. However, STPNs can easily become unwieldy
when modeling large or complex systems. Direct simulations of such dynamic models result in codes that
are often very slow to execute. Also, a simple method for parametric Petri nets is needed before highly
redundant, large-scale systems can be modeled easily. Event graphs however can model very large and
complex systems easily.
23.4.2 Mapping Petri Nets into Event Relationship Graphs
Let P denote the set of places and T the set of transitions in the STPN. We also define
d(t) =Delay time (possibly random) for each transition t ∈T
{I
p
(t),O
p
(t)} =Set of input and output places for t ∈T
{I
t
(p),O
t
(p)} =Set of all input and output transitions for p ∈P
The algorithm for translating an STPN into an ERG is as follows:
Step 0. ∀p ∈ P: define an integer state variable, X(p).
Step 1. ∀ t ∈ T: create two event vertices, O(t) and D(t) (denoting the origin and destination of a
transition) and an arc (O(t), D(t)) with delay d(t).
Step 2. ∀ p ∈ P with unique (I
t
(p), O
t
(p)) pair: create the arc (D(I
t
(p)), O(O
t
(p))) with the condition
that all p ∈ I
p
(O
t
(p)) are marked. (For inhibitor arcs, the arc condition is that the input places must
not be marked.)
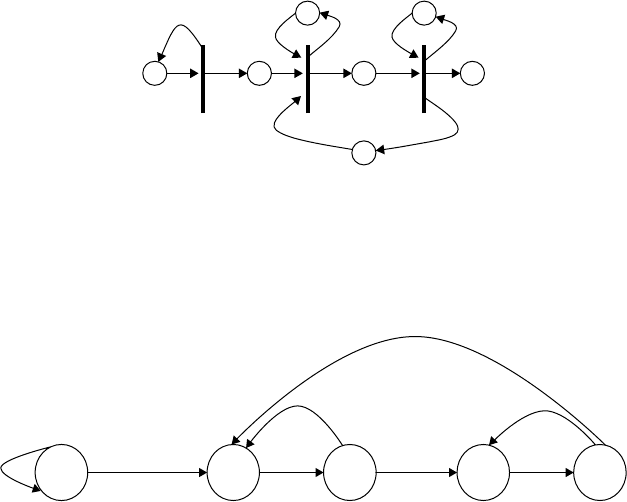
23-12 Handbook of Dynamic System Modeling
AQ2
R1 R2
B
t
a
t
s1
t
s2
Q1
FIGURE 23.13 An STPN for a communications channel with limited packet capacity.
t
a
{Q1⫹⫹;}
(R1&&B)
/
t
S1
{Q1⫺⫺;
R1⫺⫺;
B⫺⫺;}
t
S2
{R1⫹⫹;
Q2⫹⫹;}
{R2⫺⫺;
Q2⫺⫺;}
{R2⫹⫹;
B⫹⫹;}
/
/
\
/
(Q1&&B)
(Q2)
(Q1&&R1)
(R2)
FIGURE 23.14 An ERG for a tandem communications channel with limited message packet capacity.
Step 3. Add state changes:
for O(t), decrement X(p) ∀p ∈ I
p
(t);
for D(t), increment X(p) ∀p ∈ O
p
(t).
Step 4. Initialize the values of state variables in the ERG to the initial markings of the STPN.
This algorithm generalizes some of the more intuitive ideas in Schruben and Yucesan (1994). The algorithm
applied to the STPN in Figure 23.11 results in the ERG in Figure 23.5 after elimination of some redundant
events needed by the Petri net (Yucesan and Schruben, 1992).
Our second example is a buffered tandem queue with limited buffer size (channel bandwidth) between
the two resources—a sending resource R1 and a receiving resource R2. Here, we model communications
blocking with limited concurrent message packet capacity B between the two resources. The STPN model
for this system is given in Figure 23.13.
Applying the translation algorithm given earlier to this model results in the ERG given in Figure 23.14.
The arc conditions in Figure 23.14 are not shown; these conditions simply require that all state variables
decremented in the arc’s destination vertex are positive. In Figure 23.14, the “++” notation from C is used:
X++ means X is incremented by 1 (X=X+1) and X−−means X is decremented by 1 (X=X−1).
ERGs are more general and typically more parsimonious than basic STPNs for modeling discrete-event
dynamic systems. Petri nets have an intuitive graphical representation of resource contention. The two
modeling paradigms are most effectivewhen used together. Basic STPNs can be used to develop an intuitive
high-level model of resource contention for a single component. These STPNs should then be translated
to ERGs for efficient simulation. In cases where STPNs are impossibly cumbersome, parametric ERGs can
be very compact and effective in capturing the system dynamics.

Modeling Causality with Event Relationship Graphs 23-13
t
a
t
s
~
~
{Q⫽Q⫹1}
{Q⫽Q⫺B),
R⫽R⫺1}
{R⫽R⫹1}
Arrive Start Finish
(R⬎0)&&(QⱖB)
(QⱖB)
FIGURE 23.15 Batch processing with parallel resources (b, batch size; r, idle resources; t
s
service times; t
a
, interarrival
times).
23.4.3 Process Interaction Flows
It is easy to model process flows by considering the subgraph of an ERG that models the action of a
resource (e.g., the START and LEAVE nodes in Figure 23.5) as a single “process” node. When these nodes
are combined into a single node then the ERG becomes a flow graph for modeling transient entity flows.
23.4.4 Generalized Semi-Markov Processes
A Generalized semi-Markov Processes (GSMP) is a mathematical construction, consisting of sets of events,
event clocks, and states for modeling discrete-event dynamic systems. GSMPs have been used extensively to
prove various mathematical properties of models and analysis methodologies. GSMPs are not general, but
the class of systems they model is large and includes many interesting systems. However, GSMPs are abstract
and provide very little insight into the systems being modeled. Like Petri nets, GSMPs can be mapped into
ERGs using the algorithm in Schruben and Savage (1996). Representing GSMPs as ERGs allows visualiza-
tion of a system that can be used to give intuitive interpretations to some of the mathematical properties
for particular GSMPs. An example is the conditions on a GSMP for asymptotic consistency of infinitesimal
perturbation analysis gradient estimators for simulation response optimization. In Freimer and Schruben
(2001) these properties are expressed as intuitive structural properties of their ERG representations.
23.4.5 Mathematical Optimization Programs
2
The dynamics of continuous systems are often modeled by a system of differential equations that express
the relationships between changes in the values of system state variables. Given an initial state (boundary
condition) these equations completely specify a model of the system’s dynamic behavior. When this system
of differential equations is particularly simple or has some special properties, it can be solved analytically to
find the system’s path of motion (trajectory). However, many interesting models are too complex and must
be simulated by numerically solving (integrating) the set of differential equations. If the system is modeled
using random processes, then the simulations can be used to generate sample paths for statistical analysis.
In an analogous manner, the relationships between changes in the values of state variables in a discrete-
event system (events) can be modeled with an ERG. The vertices of the graph represent changes in state
and the arcs the dynamic and logical relationships between these changes. An ERG, along with initial
conditions, completely specifies the discrete-event system dynamics. Also, like for continuous systems,
the dynamics of most discrete-event systems are complex and must be numerically simulated. In this
section, we look at some properties of discrete-event models that allow us to solve, analytically, a system
of difference equations represented in their ERGs.
A simple ERG models will be used as examples. Figure 23.15 is a simple batch processing system with
parallel resources.
2
Source: This section is largely adapted from Schruben 2000, used with permission.
