Fishwick P.A. (editor) Handbook of Dynamic System Modeling
Подождите немного. Документ загружается.

22-4 Handbook of Dynamic System Modeling
and defining the error gradient based on that,
∇
ij
E =
∂E
∂w
ij
(22.4)
It is possible to use a simple steepest descent algorithm to find a local minimum:
w
ij
=−η∇
ij
E (22.5)
where η is a scaling constant. The gradient in this equation can be computed by a simple equation
w
ij
=−η
∂E
∂net
i
a
j
(22.6)
where
∂E
∂net
i
=
a
i
(1 −a
i
)(a
∗
i
−a
i
)ifi is an output element
a
i
(1 −a
i
)
k
w
ki
∂E
∂net
k
otherwise
(22.7)
This technique (proposed by Werbos [1994] and popularized by Rumelhart et al. [1986]) will lead the
CN to adopt a weight configuration that represents a local minimum in the error space, E. While many
theoretical approaches to finding global optima instead of local ones have been proposed, in practice, most
applications rely on restarting the system with a different set of random initial weights (i.e., a different
starting point in the weight space) as a simple method to avoid local minima.
22.3 Spatio-Temporal Connectionist Networks
SCNs are CNs with a temporal delay associated with their connections and therefore no need of restrictions
on cyclical connectivity. By using the activation values of PEs at one time step to compute the activation
values of PEs at another step, a form of feedback is created that makes SCNs dynamical systems. With
proper connectivity, the feedback can be used to serve as an internal memory of old states and inputs, to
induce oscillatory activation patterns, and even implement chaotic dynamics. In fact, by the same approach
that allows CNs to serve as universal function approximators, SCNs can be universal dynamical systems.
22.3.1 Basic Approach
The operation of an individual PE in an SCN can be summarized by the following general equation:
a
i
(t) = f
⎛
⎝
j
t
t
=0
w
ij
(t
) ·a
j
(t −t
)dt
⎞
⎠
(22.8)
where a
i
(t) represents the activation of PE i at time t, f () is a transfer function, j an index over the PEs
connecting to i, t
a variable integrated over time from t
=0tot
=t, w
ij
(t
) a function giving the weight
of influence of the activation of element j as a function of time, and a
j
(t −t
) the activation of element j at
time t −t
. Note that this equation replaces the simple weight in Eq. 22.1 with a temporal weight kernel.
In most applications, time is assumed to be sampled at discrete unit time intervals so the integration in
Eq. 22.8 can be replaced by a summation. In other words, we implement a discrete time simulation of a
continuous time model with synchronous updates. Further, while there have been a number of studies of
varying weight kernels (see, e.g., Mozer, 1994), most SCNs rely on the simplest of kernels: an impulse of
delay 1. In this popular, degenerate case
a
i
(t) = f
j
w
ij
·a
j
(t −1)
(22.9)
Spatio-Temporal Connectionist Networks 22-5
Input
Hidden
Context
Output
1
(a)
InputContext
PEs
(b)
Context Input
xxxxxxxxx
PEs
(c)
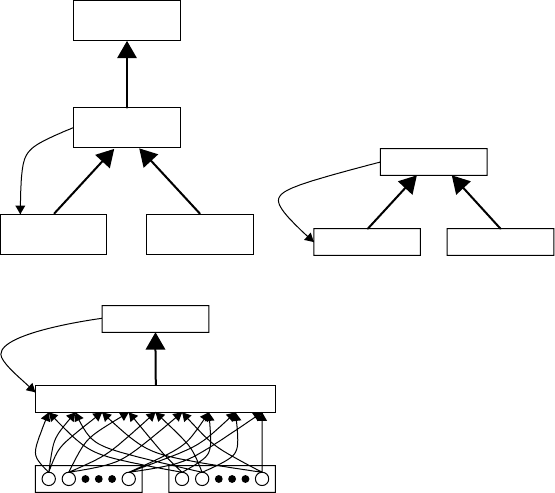
FIGURE 22.2 The most popular SCNs. (a) Elman network (From Elman, J. L. (1990). Cognitive Science 14, 179–211;
Elman, J. L. (1991). Machine Learning 7(2/3), 195–226.) (b) Williams and Zipser network (From Williams, R. J. and
D. Zipser (1989). Neural Computation 1(2), 270–280.) (c) Giles et al. network.
22.3.2 Specific Architectures
A number of specific architectures have been proposed and, as in the acyclic CN, they are organized into
layers. Owing to the cyclical nature of the connections in SCNs, it is useful to illustrate them by showing
the same layer at a given time step and also at a previous time step. By convention, the layer’s previous
time step is referred to as a context layer. The context layer is a virtual layer that does not involve any
computation and merely serves to better illustrate the operation of the network. Some of the most popular
SCN architectures are: the Elman network, the Williams and Zipser network, and the Giles et al. network.
22.3.2.1 Elman
In the Elman network (Elman, 1990, 1991), Figure 22.2(a), an input layer is connected to a hidden layer
which in turn is connected to an output layer. A virtual context layer is really the hidden layer at the
previous time step. The context layer also connects to the hidden layer, providing a simple feedback loop
from the activation vector of the hidden layer at the previous time step to the current activation vector of
the hidden layer.
22.3.2.2 Williams and Zipser
In the Williams and Zipser network (Williams and Zipser, 1989), Figure 22.2(b), the input layer is
directly connected to all activation computing PEs, which in turn have time-delayed connections back
to themselves. A subset of the PEs are used to represent the output of the network.
22.3.2.3 Giles et al.
In the Giles et al. network (Giles et al., 1990), second-order multiplicative elements are used. Thus,
the activation of each PE is computed based on a sum of products. Each product is computed by

22-6 Handbook of Dynamic System Modeling
multiplying the activation value of a PE with the activation value of an input element. Thus, the governing
equation is
a
i
(t) = f
j,k
w
ijk
·a
j
(t −1) ·a
k
(22.10)
where j represents an input element and k a regular PE.
22.3.2.4 Other Architectures
A plethora of other architectures and variants on these three approaches have been developed, but a
comprehensive survey is beyond the scope of this chapter. Interested readers are referred to Kremer (2001)
and Barreto et al. (2003).
22.4 Representational Power
One issue of particular interest to researchers working with SCNs has been an examination of their
computational power and their representation ability relative to other systems previously studied. The
question asked is: as a class of systems, what can SCNs do? It is easiest to formulate an answer to this question
in the context of other systems and two spring immediately to mind: (1) formal models of computation
and (2) dynamical systems. The former are used to model digital computers and include finite-state
automata, pushdown automata, Turing machines, and similar mathematical models of computers and
their programs. The latter are generalized mathematical models involving time.
The computational power of SCNs has been extensively studied. The paradigm is inherently capable of
universal dynamical system approximation (by a trivial corollary of the universal function approximation
capability of CNs). This means that since CNs can implement any mathematical function, SCNs can also
implement any dynamical system that can be specified mathematically to an arbitrarily close approxi-
mation. Beyond this, much focus has been placed on comparisons of specific SCN models with formal
models of computation. These formal models rely on discrete input symbols. By encoding these inputs to
vectors, SCNs can be applied to the same classes of models as finite-state automata, pushdown automata,
and Turing machines.
Not surprisingly (given the universal dynamical system approximation), it can be shown that SCNs
can exhibit the same or superior computational powers to their conventional counterparts. For example,
Kremer (1995) shows that Elman networks are capable of implementing arbitrary finite-state automata,
Wiles et al. (2001) prove that SCNs are capable of implementing pushdown automata models in their
internal dynamics, and Siegelmann (2001) showed that not only can Turing machines be represented but
they also may even be able to compute more efficiently when implemented in these continuous dynamical
systems thus exhibiting super-Turing capabilities (though the existence of hypercomputation in itself is
debatable).
A particularly interesting approach to relating SCN power to the conventional spectrum of computa-
tional formalisms is that of Giles et al. (1990). The Giles network is designed in such a way that the weights
between the products of input/context elements and subsequent PEs correspond exactly to transitions in a
traditional finite-state automaton. This correspondence allows the authors to naturally encode finite-state
automata into these networks (Giles and Omlin, 1992) an even extract automata from trained SCNs (Giles
et al., 1992). The extraction of automata from SCNs is somewhat controversial, however, and some have
argued that the effort is futile (Kolen, 1994).
22.5 Learning
The impressive representational powers of SCNs gives confidence in their use on a broad range of applica-
tions. This leads one naturally to consider the matter of learning. Forthis, we are typicallyinterested in map-
ping, not one vector (like in CNs), but rather a sequence of input vectors presented at each time step into not
one vector but rather a sequence of output vectors. Thus, the system is trained to act as a vector-sequence to
Spatio-Temporal Connectionist Networks 22-7
Hidden
InputContext
Output
Hidden (t)
Input (t)Context (t)
Output (t)
Hidden (t 1)
Input (t 1)Context (t 1)
Hidden (t 2)
Input (t 2)Context (t 2)
Hidden (t 3)
Input (t 3)Context (t 3)
Hidden (t 4)
Input (t 4)Context (t 4)
(a)
(b)
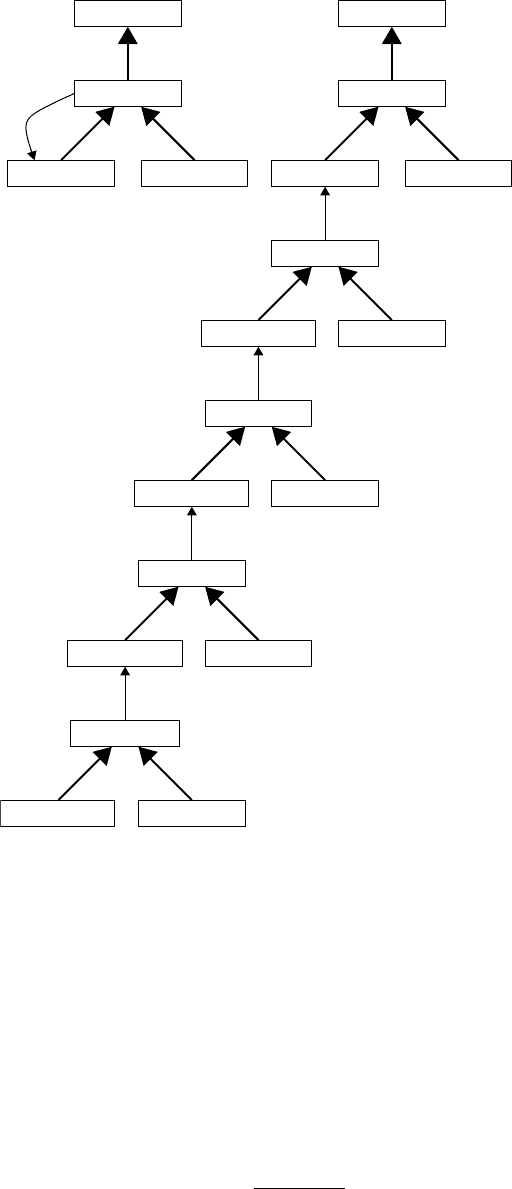
FIGURE 22.3 Unfolding an SCN.
vector-sequence mapping system. In this case, we define the output error as an error over the output vectors
over time (usually summing the error values of the output over all the time steps). It turns out that com-
puting error derivatives in the weight space of an SCN is a simple extension of the CN training algorithm.
One of the simplest methods for computing such derivatives involves unrolling a network in time using
the contextelement trick over and overagain to trace activation dynamicsback to the veryfirst time step. For
example, consider the Elman network in Figure 22.3(a). We can unfold this network for four time steps to
producethe unfolded network shown in Figure 22.3(b). In the resulting network, the connections from hid-
den to context and input to hidden at all levels of unfolding are identical. Thus, the chain rule for derivatives
allows the weight changes to each virtual set of connections to be summed to compute the gradient.
w
ij
=−η
t
∂E
∂net
i
(t +1)
a
j
(t) (22.11)

22-8 Handbook of Dynamic System Modeling
where
∂E
∂net
i
(t +1)
=
a
i
(t +1)(1 −a
i
(t +1))(a
∗
i
(t +1) −a
i
(t +1)) if i is an output element
a
i
(t +1)(1 −a
i
(t +1))
k
w
ki
∂E
∂net
k
(t+2)
otherwise
(22.12)
This method is a quick way of computing the error gradient in weight space, but requires memory to store
all the successive activation values and partial derivatives in the unfolded network. This implies a memory
requirement in the order of the number of time steps.
Interestingly, Elman himself does not unroll the network in the way described. Instead, he uses a
truncated version of gradient descent that ends the gradient computation at the virtual context layer.
This effectively results in an approximation to the gradient, which ignores distal effects in favor of more
proximal ones. This algorithm uses a fixed amount of memory and greatly reduces the computational time
since only one step of backpropagation needs to be performed.
Williams and Zipser (1989) propose an alternative approach to gradient computation where memory
usage is constant, but the computational time increases by a factor proportional to the number of PEs.
Another algorithm (Schmidhuber, 1992) combines the unrolling approach with that of Williams and
Zipser to get the best of both worlds. Some interesting dynamical systems can be induced using these
methods, for an extensive set of examples, the reader is referred to Pearlmutter (2001).
Unfortunately, however, the story does not end there. It turns out that computing the gradient is not an
effective method for training SCNs. Specifically, for problems where information must be retained for long
time periods, gradient approaches break down. Consider a problem where a network must remember the
first bit in a long binary sequence. To store this bit, the information must be effectively latched within the
PEs of the network. This requires the system to adopt a stable dynamic. Such a dynamic, however, requires
the PEs to operate in the flat outer regions of the transfer function f (). But, in these flat outer regions
the error gradient approaches zero. As a consequence, when an SCN faces a problem requiring the stable
storage of information over long-time periods, it typically is unable to learn such behavior because the
closer the PEs come to stable operation, the slower the learning gets and shorter-term effects dominate the
training process. This phenomenon is known as the shrinking gradients problem (Hochreiter et al., 2001).
Interestingly, this limitation was not discovered for some time and these networks were applied to
a number of problems without this limitation ever becoming apparent. The reason for this is that the
limitation described here, while mathematically significant, does not occur in many problems to which
these networks are typically applied. In fact, many of the models of human language actually benefit from
such a limitation as it can help to describe the limitations of human performance in comparison to formal
grammar models.
Nonetheless, a number of remedies have been suggested to the shrinking gradients problem. These
include the long short-term memory network (Hochreiter and Schmidhuber, 1997) and other training
algorithms (Palmer and Kremer, 2005). The long short-term memory approach relies on the use of
linear memory elements fed by gating elements to ensure that gradients do not deteriorate to zero. The
linear activation function guarantees that gradients do not deteriorate, while the gating elements ensure a
nonlinear dynamics which would limit the operation of the system to linearly separable problems only.
22.6 Applications
A number of applications of SCNs have been proposed and developed. For example, in Prokhorov et al.
(2001), an SCN is presented as a general purpose controller. This controller is applied to a plant that is a
third-ordersystemwith two inputs and two outputs, and to the problemof financial portfolio optimization.
Tabor (2001) has shown that the domain of linguistics can be tackled by an adaptive SCN. Specifically, he
uses dynamical systems theoryembodied in the SCN to provide effective formal models of structures in nat-
ural languages. His work provides empirically reproducible predictions of human language performance.

Spatio-Temporal Connectionist Networks 22-9
Bakker and Schmidhuber (2004) used SCNs to implement learning and subgoal discovery in robots.
This work applies to problems such as robot soccer and other tasks, where machines must dynamically
adapt strategies to a changing environment.
Eck and Schmidhuber (2002) applied SCNs to learning long-term structure in music. This can be
applied to both analysis and composition.
22.7 Conclusion
In this chapter, we have seen how spatio-temporal connectionist networks are a type of dynamical system.
These models are loosely based on abstractions of neuronal processing and typically incorporate a learning
mechanism. It is easy to extolthe inherent computational capabilities of these systems, as they can be proven
to be just as powerful as the best digital computers, capable of computing anything that is computable
by a Turing machine (the formal definition of computable) and capable or representing any dynamical
system to an arbitrary degree of precision. There are a number of learning algorithms proposed for these
systems. The simplest of these suffer from an interesting limitation called the shrinking gradients problem.
This problem identifies a mathematical limitation to what can be learned, but does not always apply to
practical problems. A few solutions to the shrinking gradients have been recently proposed. SCNs have
been successfully applied to a number of interesting real-world problems.
References
Bakker, B. and J. Schmidhuber (2004). Hierarchical reinforcement learning based on subgoal discovery and
subpolicy specialization. In F. Groen, N. Amato, A. Bonarini, E. Yoshida, and B. Krse (Eds.), Proceed-
ings of the 8-th Conference on Intelligent Autonomous Systems, IAS-8, Amsterdam, The Netherlands,
pp. 438–445.
Barreto, G. A., A. F. R. Araújo, and S. C. Kremer (2003). A taxonomy for spatio-temporal connectionist
networks revisited: The unsupervised case. Neural Computation 15(6), 1255–1320.
Eck, D. and J. Schmidhuber (2002). Learning the long-term structure of the blues. In J. Dorronsoro (Ed.),
Artificial Neural Networks — ICANN 2002 (Proceedings), pp. 284–289. Berlin: Springer.
Elman, J. (1990). Finding structure in time. Cognitive Science 14, 179–211.
Elman, J. L. (1991). Distributed representations, simple recurrent networks and grammatical structure.
Machine Learning 7(2/3), 195–226.
Giles, C., G. Sun, H. Chen, Y. Lee, and D. Chen (1990). Higher order recurrent networks & grammatical
inference. In D. S. Touretzky (Ed.), Advances in Neural Information Processing Systems 2, San Mateo,
CA, pp. 380–387. Morgan Kaufmann.
Giles, C. L. and T. Maxwell (1987). Learning, invariance, and generalization in high-order neural networks.
Applied Optics 26(23), 4972–4978.
Giles, C. L., C. B. Miller, D. Chen, G. Z. Sun, H. H. Chen, and Y. C. Lee (1992). Extracting and learning an
unknown grammar with recurrent neuralnetworks. In J. E. Moody, S. J. Hanson, and R. P. Lippmann
(Eds.), Advances in Neural Information Processing Systems 4, San Mateo, CA, pp. 317–324. Morgan
Kaufmann.
Giles, C. L. and C. Omlin (1992). Inserting rules into recurrent neural networks. In S. Kung, F. Fallside,
J. A. Sorenson, and C. Kamm (Eds.), Neural Networks for Signal Processing II, Proceedings of the 1992
IEEE Workshop, Piscataway, NJ, pp. 13–22. IEEE Press.
Hochreiter, S., Y. Bengio, P. Frasconi, and J. Schmidhuber (2001). Gradient flow in recurrent nets: The
difficulty of learning long-term dependencies. In J. F. Kolen and S. C. Kremer (Eds.), A Field Guide
to Dynamical Recurrent Networks, pp. 237–244. Piscataway, NJ: IEEE Press.
Hochreiter, S. and J. Schmidhuber (1997). Long short-term memory. Neural Computation 9(8),
1735–1780.
22-10 Handbook of Dynamic System Modeling
Hornik, K., M. Stinchcombe, and H. White (1989). Multilayer feedforward networks are universal
approximators. Neural Networks 2(5), 359–366.
Kolen, J. F. (1994). Fool’s gold: Extracting finite state machines from recurrent network dynamics. In
J. D. Cowan, G. Tesauro, and J.Alspector (Eds.), Advances in Neural Information Processing Systems 6,
Volume 6, pp. 501–508. San Mateo, CA: Morgan Kaufmann.
Kremer, S. C. (1995). On the computational power of elman-style recurrent networks. IEEE Transactions
on Neural Networks 6(4), 1000–1004.
Kremer, S. C. (2001). Spatio-temporal connectionist networks: A taxonomy and review. Neural
Computation 13(2), 249–306.
McCulloch, W. and W. Pitts (1943). A logical calculus of ideas immanent in nervous activity. Bulletin of
Mathematical Biophysics 5, 115–133.
Mozer, M. C. (1994). Neural net architectures for temporal sequence processing. In A. Weigend and
N. Gershenfeld (Eds.), Time Series Prediction, pp. 243–264. Reading, MA: Addison-Wesley.
Palmer, J. and S. Kremer (2005). Learning long-term dependencies with reusable state modules and
stochastic correlation. In Intelligent Engineering Systems Through Artificial Neural Networks, Volume
15, pp. 103–109. ASME.
Pearlmutter, B. (2001). Gradient calculations for dynamic recurrent networks. In J. F. Kolen and
S. C. Kremer (Eds.), A Field Guide to Dynamical Recurrent Networks. pp. 179–206. Piscataway,
NJ: IEEE Press.
Prokhorov, D., G. Puskorius, and L. Feldkamp (2001). Dynamical recurrent networks in control. In
J. F. Kolen and S. C. Kremer (Eds.), A Field Guide to Dynamical Recurrent Networks. pp. 143–152.
Piscataway, NJ: IEEE Press.
Rumelhart, D., G. Hinton, and R. Williams (1986). Learning internal representation by error propagation.
In J. L. McClelland, D. Rumelhart, and the P. D. P. Group (Eds.), Parallel Distributed Processing:
Explorations in the Microstructure of Cognition, Volume 1: Foundations. Cambridge, MA: MIT Press.
Schmidhuber, J. H. (1992). A fixed size storage o(n
3
) time complexity learning algorithm for fully recurrent
continually running networks. Neural Computation 4(2), 243–248.
Siegelmann, H. (2001). Universal computation and super-turing capabilities. In J.F. Kolen and S. C. Kremer
(Eds.), A Field Guide to Dynamical Recurrent Networks, pp. 143–152. Piscataway, NJ: IEEE Press.
Tabor, W. (2001). Sequence processing and linguistic structure. In J. F. Kolen and S. C. Kremer (Eds.),
A Field Guide to Dynamical Recurrent Networks, pp. 291–310. Piscataway, NJ: IEEE Press.
Werbos, P. J. (1994). The Roots of Backpropagation: From Ordered Derivatives to Neural Networks and
Political Forecasting. New York: Wiley.
Wiles, J., A. Blair, and M. Bodén (2001). Representation beyond finite states: Alternatives of push-down
automata. In J. F. Kolen and S. C. Kremer (Eds.), A Field Guide to Dynamical Recurrent Networks,
pp. 129–142. Piscataway, NJ: IEEE Press.
Williams, R. J. and D. Zipser (1989). A learning algorithm for continually running fully recurrent neural
networks. Neural Computation 1(2), 270–280.

23
Modeling Causality with
Event Relationship
Graphs
Lee Schruben
University of California
23.1 Introduction ................................................................ 23-1
23.2 Background and Definitions ...................................... 23-2
Discrete-Event Systems and Models
•
Discrete-Event
System Simulations
•
The Basic Event Relationship
Graph Modeling Element
•
Verbal Event Graphs
•
Reading Event Relationship Graphs
23.3 Enrichments to Event Relations Graphs .................... 23-7
Parametric Event Relationship Graphs
•
Building
Large and Complex Models
•
Variations of Event
Relationship Graphs
23.4 Relationships to Other Discrete-Event System
Modeling Methods .................................................... 23-10
Stochastic Timed Petri Nets
•
Mapping Petri Nets
into Event Relationship Graphs
•
Process Interaction
Flows
•
Generalized Semi-Markov Processes
•
Mathematical Optimization Programs
23.5 Simulation of Event Relationship Graphs ............... 23-16
23.6 Event Relationship Graph Analysis .......................... 23-16
23.7 Experimenting with ERGs ........................................ 23-17
23.1 Introduction
Events are any potential change in the state of a dynamic system. Event relationship graphs (ERGs)
explicitly model the ways in which one system event may cause another system event to occur. The cause
and effect relationships between events modeled in an ERG, along with simple rules for execution and
initial conditions, completely specify all possible sample paths (state trajectories) of a dynamic system
model. Continuous dynamics systems have been modeled as ERGs, but they are most commonly used
to model discrete-event system dynamics. The ERG for a queueing system is typically a system of simple
difference equations analogous to a system of differential equations used in modeling continuous time
system dynamics. ERGs are completely general in that any dynamic system can be modeled as an ERG
(Savage et al, 2005). They are easy to develop and understand and facilitate the design of efficient simulation
models. ERGs also have analytical representations that aid in systems analysis, specifically when the
potential system trajectories for ERG model are represented as the solutions to mathematical optimization
problems.
23-1

23-2 Handbook of Dynamic System Modeling
23.2 Background and Definitions
1
23.2.1 Discrete-Event Systems and Models
It will be sufficient for our purposes to define a“system”as a collection of entities that interact with a common
purpose according to sets of laws and policies. A system may already exist, or it may be hypothetical or pro-
posed. Here, we intentionally do not define a system by the specific elements in it or its boundaries. Rather,
we define a system by its purpose. Thus, we speak of a communications system, a health care system, and a
production system. Using a functional definition of a system helps avoid thinking of a system as having a
preconceived structure. Consequently, a system is viewed in terms of how it ought to function rather than
how it currently functions. To design better systems it is important to think beyond the status quo.
The “entities” making up the system may be either physical or mathematical. A physical entity might
be a patient in a hospital or a part in a factory; a mathematical entity might be a variable in an equation.
When developing models of queueing systems, it is often useful to classify entities as being either resident
entities or transient entities. Resident entities remain part of the system for long intervals of time, whereas
transient entities enter into and depart from the system with relative frequency. In a factory, a resident
entity might be a machine; a transient entity might be a job or a part. Depending on the level of detail
desired, a factory worker might be regarded as a transient entity in one model and a resident entity in
another. The states of resident entities can often be modeled sufficiently on a computer using simple
fixed-dimension integer arrays, while transient entities often require creating and maintaining dynamic
records or objects. Entities are described by their characteristics (referred to here as attributes). Attributes
can be quantitative (represented in a computer by numeric codes) or qualitative. Moreover, they can be
static and never change (the speed of a machine), or they can be dynamic and change over time (the length
of a waiting line). Dynamic attributes can further be classified as deterministic or stochastic depending on
whether the changes in their values can be predicted with certainty or not.
The rules that govern the interaction of entities in a system that are not under our control are called
“laws.” Similar laws are grouped in families, members of which are distinguished by parameters. Rules that
are under our control are called “policies”; a family of similar policies may be distinguished by the values
of their factors.
We will define a model simply as asystemusedasasurrogateforstudyinganothersystem.In this chapter,
when we use the word system, without qualification, we are referring to a real or hypothetical system that is
the subject of a modeling analysis or simulation study. In typical computer simulation models, systems of
mathematical equations and computational objects are used as a surrogate for a real or proposed system
of physical entities.
The state of a system is a complete description of the system and includes values of all attributes of
entities, parameters of laws, factors for its policies, time, and what might be known about the future.
The state space is the set of all possible system states. A process is an indexed sequence of system states;
typically, the index is time, but it might be the index of jobs in a queueing system or some other system
characteristic.
A discrete-event model of a dynamic system is one where the state of the system changes at particular
instants of time. Examples include queueing system models where a job arriving or leaving the system is
a discrete change in the system state. Changes in the system state for a discrete-event system are called
events. In a production system, for example, events might include the following:
1. Completion of a machining operation; such an event might be called “finish” and the state of the
machine involved would change from “busy” to “idle.”
2. Failure of a machine; a “failure” event would change the machine state to “broken.”
3. Arrival of a repair crew; an event called, say, “start_repair” where the machine state would change
to “under_repair.”
1
Source: Figures, examples, and model descriptions in this chapter are adapted from Schruben, D. L. and
L. W. Schruben, Event Relationship Graph Modeling Using SIGMA. ©Custom Simulations, used with permission.
Modeling Causality with Event Relationship Graphs 23-3
4. Arrival of a part at a machining center; this “arrival” event would, if an appropriate machine were
idle and in good working condition, immediately cause another event, a “start_processing” event
where the machine will again become “busy.”
The ability to identify and abstract system events in a discrete-event model are important skills that
take practice to acquire. The following simple steps identify system events: first, identify all the dynamic
attributes of the system entities; then, identify the circumstances (state conditions and/or time delays) that
may cause the values of these attributes to change. These circumstances are the system events and they will
in turn schedule or cancel other system events.
23.2.2 Discrete-Event System Simulations
We model (verb) the dynamic behavior of a discrete-event system by describing the events and the rela-
tionships between these events. When we use the word model (noun), without qualification, we will be
referring to a graphical description of a system called an ERG. Simulations will refer to computer programs
developed from ERGs. Simulations will be our methodology for studying the model.
The building blocks of a discrete-event simulation program are event procedures. Each event procedure
makes appropriate changes in the state of the system and, perhaps, may schedule a sequence of further
events to occur. Event procedures might also cancel previously scheduled events. An example of event
canceling might occur when a busy computer breaks down. End-of-job events that might have been
scheduled to occur in the future must now be canceled (these jobs will not end in the normal manner as
originally expected).
The event procedures describing the state changes in a discrete-event system simulation are executed
by a main control program that operates on a master appointment list of scheduled events. This list is
called the pending events list and contains all of the events that are scheduled to occur in the future. The
main control program will advance the simulated time to the time for the next scheduled event. The
corresponding event procedure is executed, typically changing the system state and perhaps scheduling
or canceling further events. Once this event procedure has finished executing, the event is removed from
the future events list. Then the control program will again advance time to the next scheduled event and
execute the corresponding event procedure. The simulation operates in this way, successively calling and
executing the next scheduled event procedure until some condition for stopping the simulation run is met.
The operation of the main simulation event scheduling and execution loop is shown in Figure 23.1.
23.2.3 The Basic Event Relationship Graph Modeling Element
ERGs are a way of explicitly expressing all the relationships between events in a discrete-event dynamic
system model. Some early references include Schruben (1983), Sargent (1988), Som and Sargent (1990),
and Wu and Chung (1991). ERG models of discrete-event system dynamics have been presented in many
textbooks on simulation, stochastic processes, and manufacturing systems engineering (Pegden, 1986;
Hoover and Perry, 1990; Law and Kelton, 2000; Askin and Standridge,1993; Nelson, 1995; Seila et al., 2003).
The three elements of a discrete-event system model are the state variables, the events that change the
values of these state variables, and the relationships between the events (one event causing another to
occur, or preventing it from occurring). An ERG organizes sets of these three objects into a simulation
model. In the graph, events are represented as nodes (circles) and the relationships between events are
represented as arcs (arrows) connecting pairs of event nodes. The basic unit of an ERG is an arc connecting
two nodes. Suppose the arc represented in Figure 23.2 is part of an ERG.
We interpret the arc between A and B as follows: whenever event A occurs, it might cause event B to occur.
Arcs between event nodes are labeled with the conditions under which one event will cause another event
to occur, perhaps after a time delay. The state changes associated with each event are in braces next to the
event node.
ERGs may look similar to flow graphs, but they are very different. While one might sometimes think of
these graphs as modeling the flow of, say jobs, through a queueing system network, these graphs are actually
