Fisher John P. e.a. (ed.) Tissue Engineering
Подождите немного. Документ загружается.


mikos: “9026_c004” — 2007/4/9 — 15:50 — page6—#6
4-6 Tissue Engineering
the latter being restricted by the ECM area that is available for cell attachment. In the context of tissue
engineering applications, the spatial distribution of ECM ligands may be a powerful means for controlling
cell behavior. Using the micropatterned substrate mentioned above, a recent study showed that human
mesenchymal stem cells (MSCs) undergo osteogenesis when allowed to spread out (cell area ≈10,000 µm
2
)
but become adipocytes when confined with a small area (≈1,000 µm
2
); this shape-dependent control
of lineage commitment is mediated by the Rho GTPase, specifically via its effect on ROCK-mediated
cytoskeletal tension [51].
Finally, the studies summarized above address the spatial effect of the ECM on the extent of cell
distortion and tension in a two-dimensional cell culture system. With few exceptions, the mechanical
interaction between a cell and the ECM occurs around the whole cell surface in a true physiological setting.
While there is not yet a direct measurement method to correlate tractions and the spatial distribution of
ECM ligands in a three-dimensional system, it is likely that the correlation is similar to that in a planar
culture system.
4.3.3 Physicality of ECM Scaffolds in Tissue Engineering
The control of cell function by the ECM is a subject under vigorous investigation in the field of cell biology
and has great potential in tissue engineering applications. While most studies have previously focused
on the chemical composition of the ECM, it is becoming clear that the physicality of the ECM scaffold
is equally important as it has a profound impact on the cellular tension. Thus, design of future artificial
ECMs for tissue engineering applications should take into consideration both the chemical and physical
properties of ECM scaffolds. It is important to note that the mechanical influence between cells and ECM
scaffolds is mutual. Cells exert strong traction forces that deform and rearrange their surrounding matrix
proteins [18,41]. Hence, traction forces may affect the structure of the scaffolds (e.g., porosity, pore size,
etc.), and changes in material properties will feedback to affect cell functions. Finally, as discussed below,
cells in the body exist in a dynamic mechanical environment. Cell-scaffold constructs that are formed
in situ will inevitably experience mechanical loading. Therefore, it is important to understand how the
material properties of the scaffold will be affected by mechanical forces, and how cells embedded within
the scaffold will sense and respond to these physiologic loads transmitted through the scaffold.
4.4 The Role of Externally Applied Mechanical Forces in Cell
Function
Throughout their lifetime, cells are exposed to various kinds of mechanical forces generated during
common physiological processes. The ability to sense these external forces is not a unique property of
cells in specialized sensory organs, but instead is shared by most, if not all, cell types. Furthermore,
many nonsensory cells rely on appropriate mechanical inputs for regulating cell growth, function, and
remodeling. For example, gravitational compressive forces control the deposition of bone, and mechanical
load on skeletal muscle determines muscle mass; under conditions of diminished mechanical loading, such
as prolonged bed rest or microgravity, bone and muscle mass is quickly lost [1–3]. From an engineering
perspective, under normal conditions cells appear to convert “increases in the net external force acting on
a tissue” into “internal tension” by increasing tissue mass or other responses [33,52]. Such a response is
not always beneficial and may contribute to pathological states such as cardiac and vascular hypertrophy
that is caused by chronic high blood pressure. It is generally agreed that forces beyond the physiological
range, both over- and underloading, could lead to adverse consequences [11,45,52].
In order to influence cell growth and function, mechanical forces may trigger the same signaling
pathways that are activated by conventional chemical stimuli (e.g., growth factors and hormones). A vast
amount of data has shown that many of the biochemical events generated by cells in response to forces are
similar to those that occur following recognition of chemical stimuli (see References 3,33,45, and 52–56

mikos: “9026_c004” — 2007/4/9 — 15:50 — page7—#7
Mechanical Forces on Cells 4-7
TABLE 4.1 A Summary of Devices Used for Mechanical Stimulation of Cells In Vitro
Fluid flow
Name of device/method in and out
of developing forces Primary force of device Comments
Cone-and-plate Shear stress No Possible presence of secondary flows
Parallel-plate flow chamber Shear stress Yes Possible presence of not fully developed
laminar flow where fluid enters device
Pressure varies linearly as a function
of position, though this variation is
often ignored as it is very small
Uniaxial stretch Tensional stress No May also generate shear stress due to
motion of cells relative to fluid
Biaxial stretch Tensional stress No May also generate shear stress due to
motion of cells relative to fluid
Compression of gas phase Pressure No Change in concentration of dissolved gas
by addition of an inert gas due to nonideal behavior
Direct compression of Pressure No No gas phase present
liquid phase
Source: Adapted from Gooch, K.J. and Tennant, C.J., Mechanical Forces: Their Effects on Cells and
Tissues, Springer-Verlag, New York, 1997. With permission.
for review). The exact mechanisms by which cells transduce mechanical stimuli into biochemical signaling
events (mechanochemical transduction) are not yet clear and are an active area of research.
4.4.1 Devices and Methodology Used for Mechanical Stimulation of Cells In
Vitro
In complex in vivo environments, it is difficult to clarify the exact effect of a specific force or to delineate
the role of a specific signaling pathway in mechanotransduction processes due to the interference of
myriad chemical factors and the presence of other mechanical forces. Therefore, investigations on cellular
responses to mechanical stimulation have relied heavily on the use of in vitro systems. Table 4.1 summarizes
devices that are commonly used to subject cultured cells to flow, stretch, and pressure [52]. These devices
expose a large number of cells to well-defined mechanical stimuli that replicate physiological loading.
Techniques for applying localized forces to individual cells have been developed. The reader is referred to
other resources on the subject [2].
4.4.1.1 Shear Stress
It is possible that most cell types are exposed to fluid shearing due to interstitial flow. However, the
effects of shear stress on cell behavior have been studied most extensively in vascular endothelial cells
(ECs), as they are constantly exposed to blood flow. Two common flow systems used for in vitro studies
of shear effects on cells are the cone-and-plate viscometer and the parallel-plate flow chamber. In a
cone-and-plate device (Figure 4.3a), cells are placed on a plate that remains stationary. Medium is filled
in the space between the plate and cone and fluid flow is achieved by rotating the cone. In a parallel-
plate flow chamber (Figure 4.3b), cells are usually cultured on a glass slide that forms the floor of a
rectangular flow channel. Flow is driven to pass over the cell surface by an imposed pressure gradient.
Both devices generate macroscopically uniform shear stress acting on the surface of cells. The derivations
for describing the velocity profile and shear stress for these two devices from hydrodynamic theory are
described elsewhere [57,58]. Note that the estimated shear stress is usually nominal because only macro
(or bulk) fluid dynamics is considered. At a subcellular length scale, the magnitude and gradient of shear
stresses may vary significantly with the local cell surface topography [59–65]. In addition, the fluid is
usually assumed to be an incompressible Newtonian fluid. The assumption of incompressibility is valid if
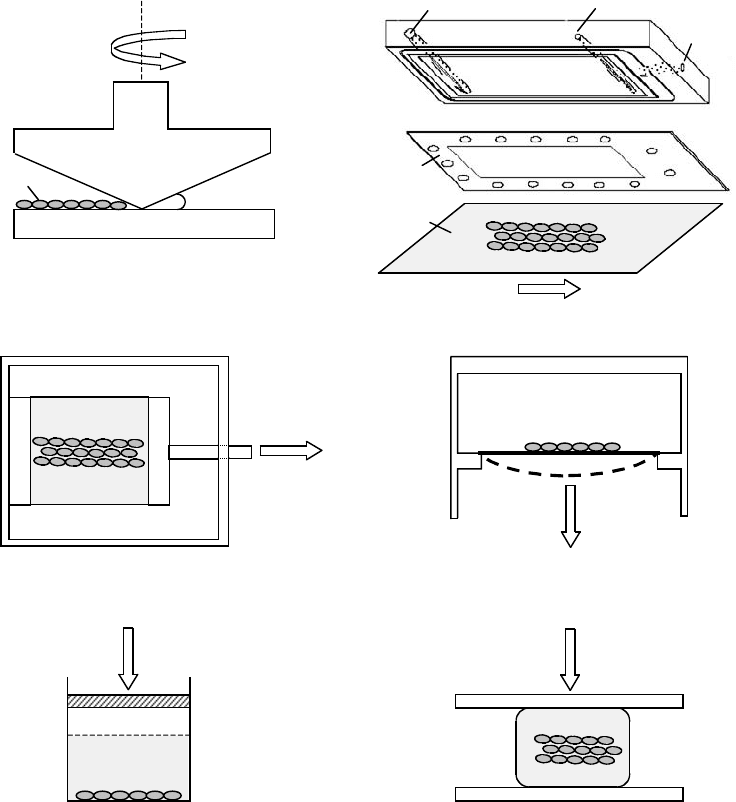
mikos: “9026_c004” — 2007/4/9 — 15:50 — page8—#8
4-8 Tissue Engineering
Cone-and-plate viscometer Parallel-plate flow chamber
Uniaxial stretch device Biaxial stretch device
Hydrostatic pressurization Platen abutment
Vacuum
Gasket
Flow direction
Flow inlet Flow outlet
Glass slide
Cells
a
ω
Stationary plate
Rotating cone
Deformed by vacuum
Load
Load
Stretch direction
Stationary end
Moving end
(a) (b)
(c) (d)
(e) (f)
FIGURE 4.3 Schematic diagrams of devices used for mechanical stimulation of cells in vitro. (a) The cone-and-plate
viscometer: cells are placed on the stationary plate and fluid flow is achieved by rotating the cone. For small cone angles
(α 1) and small rotational rates ω , shear stress is uniform throughout the fluid phase between the cone and the
plate. Although outside the scope of this chapter, it is important to note that this device is often used for studying
the effect of bulk shear stress on suspended cells such as platelets and leukocytes. (Adapted from Tran-Son-Tay, R.,
Physical Forces and the Mammalian Cell., Frangos, J.A. (Ed.) Academic Press, San Diego, 1993; Konstantopoulos, K.,
Kukreti,S., and McIntire, L.V., Adv. Drug. Deliv. Rev., 33, 141, 1998. With permission.) (b) The parallel-plate flow
chamber: the flow channel is formed by a cutout in a silicon gasket. The top plate of the flow channel is the surface of a
polycarbonate base with flow inlet and outlet. The bottom plate is a glass slide where cells are cultured. The apparatus
is held together by vacuum (shown here), clamps, or torqued screws. (c) The uniaxial device: cells are cultured on an
elastic membrane, which is subjected to elongational stretch along one axis of the membrane in plane. (d) The biaxial
device: cells are cultured on an elastic membrane, which is deformed by an applied vacuum. Solid and dashed lines
are the positions of the membrane before and under deformation, respectively. (e, f) Devices for compressive loading.
(Adapted from Brown, T.D., J. Biomech., 33, 3, 2000. With permission.) See text for details.
mikos: “9026_c004” — 2007/4/9 — 15:50 — page9—#9
Mechanical Forces on Cells 4-9
water is the dominant component of the biological fluid under investigation. Other biological fluids such
as blood, however, are non-Newtonian, and thereby limit the accuracy of the predictions [52,66].
4.4.1.2 Stretch
Many different cell types are constantly exposed to stretch during normal physiological processes. For
example, cells on the compliant aortic wall are subjected to cyclic stretch due to pulsatile blood flow, and
cells in the musculoskeletal system are subjected to cyclic stretch due to movement or gravity or both.
A common method for in vitro studies of stretch effects on cells involves culturing cells on a flexible
substrate, such as a silicone membrane, and then stretching the membrane with a controlled strain
magnitude, frequency, and duration. Cells can be exposed to uniaxial or biaxial stretch (Figure 4.3c,d).
This type of cell deformation device has several inherent problems. One problem is that the load delivered
to cells is dependent on the state of adhesion between the cells and their substrate. Cells not fully adhered to
the substrate do not experience the same amount of stretching as those fully adhered, and the subsequent
data could be misleading [52]. Another problem is that fluid shear stress is often present concurrently
with the imposed substrate deformation, due to coupled motion of the nutrient media [52,67]. Therefore,
experimental design and data interpretation need to account for the relative contribution of stretch and
shear stress.
4.4.1.3 Pressure/Compression
Hydrostatic pressurization is commonly used for investigating the effect of elevated pressure on cell
functions (Figure 4.3e) [67]. This approach is simple and can deliver static and cyclic loading. However,
the ensuing increase in the concentration of dissolved gases due to elevated pressure of the gas phase may
affect cell functions, making it difficult to determine whether the effects observed in this system result
from the pressure or from the change in gas concentration [52]. Two methods have been developed to
circumvent this problem. One is to directly compress the fluid in the absence of a gas phase, and the other
is to increase pressure by the addition of an inert gas (e.g., helium) while maintaining the partial pressure
of biologically active gases (e.g., oxygen and carbon dioxide) [52,67].
An alternative approach to achieving compressive stress is to use direct platen abutment (Figure 4.3f)
[67]. In this approach, a three-dimensional specimen (e.g., cells that are seeded in a matrix) is placed
between two flat plates; the bottom plate remains stationary, whereas the top plate is pushed downward
to deliver unconfined uniaxial compression (shown in Figure 4.3f; no peripheral support of the specimen
so that it can freely expand laterally) or confined compression. This device can deliver static and cyclic
compressive stresses. Direct platen abutment has an inherent problem that is similar to stretch devices: the
loading delivered to cells is strongly dependent on the cell–matrix adhesion. Additionally, several variables
arise concurrently with the compressive strain (e.g., flow, tensile strains, changes in specimen volume,
etc.) [45,67]. When using them for experiments, it is important to include proper controls so that the
effect due to compression can be distinguished from those due to other variables.
Finally, it should be noted that in all of the apparatuses mentioned earlier, cells usually are abruptly
exposed to an imposed mechanical stimuli from static conditions. The sudden onset of mechanical
inputs has been found to have a profound effect on some force-induced cell responses [68–72]. Detailed
numerical analysis of the stress in the device may provide information for characterizing the time history
of the mechanical stress under investigation, as well as for describing its spatial distribution and identifying
the presence of unwanted inputs [52,67].
4.4.2 Responses of Cells to Mechanical Stimulation In Vitro
There is a rapidly growing list of reports detailing force-induced cellular responses by various experimental
models as described earlier. Several excellent reviews have addressed the effects of particular forces on
specific cell types in vitro [33,45,52–56,73–80]. The intention here is to avoid repetition with other papers
and to address the general features of cellular responses to mechanical stimulation. The following discus-
sion uses the force-induced responses of vascular ECs, vascular smooth muscle cells (SMCs), osteoblasts,
mikos: “9026_c004” — 2007/4/9 — 15:50 — page 10 — #10
4-10 Tissue Engineering
and articular chondrocytes to illustrate the main points. These cell types are chosen because of the large
body of data that are available.
Generally speaking, the responses of cells to a change in their external mechanical loads can be separ-
ated into rapid responses that occur within seconds to minutes and delayed responses that develop over
many hours [45,75]. The rapid responses are due to the activation of a variety of intracellular signaling
events, including potassium channel activation, elevated intracellular free calcium concentration, inositol
trisphosphate generation, adelylate cyclase activation, G protein activation, phosphorylation of pro-
tein kinases, and, eventually activation of transcription factors [45,56,73,75]. Delayed responses usually
require the modulation of gene expression [45,56,75]. Advances in the DNA microarray technology have
allowed wide-scale screening of the genes affected by mechanical stimulation of cells, providing significant
insights into the mechanical regulation of cell functions and homeostasis. For example, it was found that
several genes related to inflammation and EC proliferation were downregulated after exposure of ECs to
an arterial level of laminar shear stress (12 dyn/cm
2
) for 24 h [81]. This finding suggests that long-term
exposure to laminar flow may keep ECs in a relatively noninflammatory and nonproliferate state, which
is consistent with the clinical observation that ECs at the straight part of arteries are mostly in a quies-
cent state and are relatively protected from the development of atherosclerotic plaques [81–85]. Reports
concerning the genomic programming of other cell types in response to mechanical stimulation are
available [86–89].
It is interesting to note that although force-induced delayed responses (and adaptive changes) vary
at the cellular level among cell types, different mechanical stimuli induce several similar biochemical
events in a variety of cells during rapid responses. For example, shear stress increases the concentration of
intracellular free calcium and enhances the production of nitric oxide and at least one type of prostaglandin
in osteoblasts, chondrocytes, SMCs, and ECs; in ECs, the above biochemical events can be induced
by either shear stress or stretch [66,90–109]. The similarity of force-induced early biochemical events
suggests that the way cells perceive different forces may be similar [52,73]. A cell may sense an imposed
external force by detecting a deformation or resistance to deformation under stress. Different forces
cause different kinds of cell deformation, thereby differentially inducing the common biochemical events
and subsequently leading to diverse long-term changes. Indeed, it has been hypothesized that similar
mechanisms might have evolved for cell recognition and response to external forces, since many cell types
are subjected to external forcesin the body, and even those thought not to be subjected to large forces in vivo
respond to mechanical forces in vitro [45,52]. However, cell type-specific mechanosensing processes and
the intrinsic heterogeneity among different cells cannot be excluded, but they are beyond the scope of this
chapter.
4.4.3 Mechanosensing of Cultured Cells to Externally Applied
Mechanical Forces
4.4.3.1 Direct Mechanosensing
Although intracellular signaling events triggered by external forces have been elucidated in many cell types,
the primary mechanosensor for transducing mechanical input into biochemical signals remains elusive.
It is hypothesized that forces may physically alter the molecular structure or displace the position of a
sensor, thereby altering/triggering chemical signal transduction events. In conjunction, mechanosensors
should be located at a site where the force acts directly or can be transmitted to efficiently [52,56,80]. Since
most forces first act directly on the plasma membrane, the majority of the mechanotransensors that have
been proposed are structures on the plasma membrane. Membrane structures that have been implicated
in the role of mechanosensors in several cell types include ion channels, G protein-linked receptors,
tyrosine kinase receptors, and integrins. Alternatively, because forces applied to the plasma membrane
are transferred to the cytoskeleton, it too could act as a mechanosensor. Any reader interested in further
details regarding the structures and signaling pathways associated with the proposed mechanosensors is
referred to other resources [5,45,52–56,73,75,79,110–116].
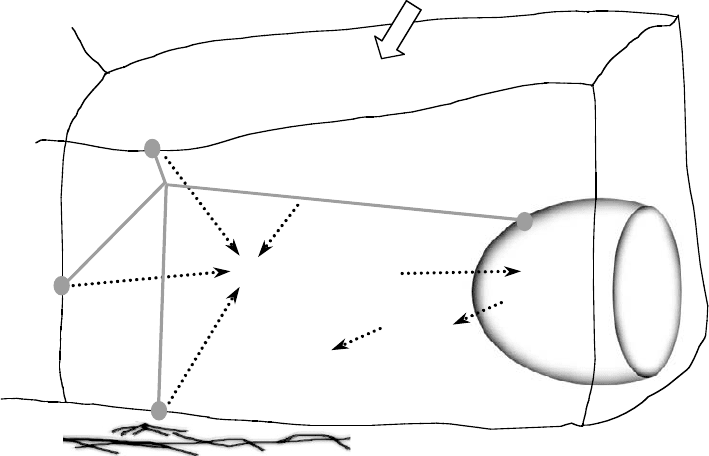
mikos: “9026_c004” — 2007/4/9 — 15:50 — page 11 — #11
Mechanical Forces on Cells 4-11
Of the proposed mechanosensors, cytoskeleton and integrins have been the most extensively studied.
Evidence suggests that they regulate mechanotransduction via mechanical and chemical mechanisms. The
chemical nature of their functions is referred to the publications listed above. The mechanical nature of
their actions is briefly considered here. As discussed in Section 4.2, an anchorage-dependent cell exists in a
state of tension that is maintained by its cytoskeleton and balanced by the surrounding matrix via integrin-
mediated adhesion sites (i.e., FAs). When an external force is loaded on the cell, the internal cellular
tension changes to equalize the external force by actively rearranging its cytoskeleton and adhesion sites.
The resulting change in cytoskeletal tension may convey a regulatory signal to the cell and subsequently
alter its functional state. Dynamic changes in cytoskeleton organization, integrin-ECM binding, FAs, and
traction forces may thus play a critical role in regulating mechanotransduction. These changes have been
observed in EC responses to shear stress [117–121].
Finally, although each of the candidates mentioned above has been proposed to be a primary mechano-
sensor, it should be noted that they have a high degree of association with one another [3,56,75,80].
Considering the vast array of signaling pathways induced by forces, it is likely that several mechanosensors
are induced simultaneously. Hence, forces may be transduced to biological signals through interactions
of activated mechanoreceptors (Figure 4.4). Such a “decentralized model” was first proposed by Davies to
describe EC responses to mechanical stresses but is applicable to mechanically induced responses in other
cell types [56,80,122]. In this model, forces acting on one region of the cell surface are also transmitted
by the cytoskeleton to other locations where signaling can occur, such as FAs at the cell–ECM interface,
cell–cell junctions, the nuclear membrane, and, in case of two-dimensional culture, membrane proteins
at the apical surface; the cytoskeleton itself is also a mechanosensor. This model predicts mechanotrans-
duction as an integrated response of multiple signaling networks that are spatially organized in the cell.
There is an increasing amount of data supporting the decentralization model (see References 13,56,75,
and 122–124 for review).
Intracellular signaling
Gene
regulation
Protein
synthesis
Apical
transmembrane proteins
Nuclear
membrane
Extracellular matrix
Cell–cell
j
unctions
Cytoskeleton
Focal adhesions
Cellular
responses
External forces
FIGURE 4.4 Model of initiation of signal transduction in cells in response to shear stress, stretch, and pressure.
Forces may directly activate individual mechanosensors or may be transmitted by the cytoskeleton to intracellular
locations where signaling can occur. In either case, cascades of intracellular signaling events are initiated, leading to
altered gene expression and cell behavior. (Adapted from Davies, P.F., Physiol. Rev., 75, 519, 1995. With permission.)
See text for details.

mikos: “9026_c004” — 2007/4/9 — 15:50 — page 12 — #12
4-12 Tissue Engineering
4.4.3.2 Indirect Mechanosensing
It is important to note that mechanical forces may be accompanied by modifications of the chemical
environment. For example, fluid flow influences the transport of agonists and other compounds to and
from the cell surface (or, the local concentration of chemicals at the cell surface). If these agonists are
degraded at the cell surface rapidly (as ATP is), flow will cause an increase in their concentration at
the cell surface, and consequently modulate the cellular response [52,56,122]. Therefore, flow-induced
responses may be mediated by increases in agonist concentrations (i.e., “indirect” mechanosensing),
rather than physical alterations of mechanosensors (i.e., “direct” mechanosensing) by shear stress. There
is in vitro experimental evidence that supports this mass transport hypothesis [125–132]. Indirect and
direct mechanosensing are not mutually exclusive. It is likely that mechanical forces are incorporated into
the biological signaling network by both physical alterations of mechanosensors and modifications of
local chemical environments.
4.4.4 Applications of Externally Applied Mechanical Forces in
Tissue Engineering
Conventional cell culture techniques grow cells under static conditions; in large-scale bioreactors (e.g.,
fluidized bed reactors, spinner flasks, rotating vessels, and perfused vessels), flow and mixing patterns
are introduced merely to enhance spatially uniform cell distributions on three-dimensional scaffolds and
provide efficient mass transfer to the growing tissues. As the significance of externally applied mechanical
forces in maintaining appropriate cell physiology has come into the light, tissue engineers have incorpor-
ated mechanical stresses into bioreactor design and found that physiological loading has positive effects
on growing cells/tissues in vitro. For example, increasing fluid shear forces significantly increases the
mineral deposition by rat marrow stromal osteoblasts in a three-dimensional titanium fiber mesh scaffold
[133,134], and the application of cyclic stretch to vascular SMCs cultured in collagen gels can help main-
tain the contractile phenotype of SMCs, align them in the correct physiological orientation, and improve
the mechanical properties of cell–gel composites [135–137]. In the context of tissue-engineered cartilage,
researchers have found that artificial cartilage grown under cyclic compressive loading has superior bio-
chemical compositions and material properties than those grown statically [138–140]. Furthermore, cyclic
compression can promote the chondrogenesis of rabbit bone-marrow MSCs by inducing the synthesis of
transforming growth factor (TGF-β1), which then stimulates the MSCs to differentiate into chondrocytes
[141]. These results show that appropriate mechanical stimulation may be a determining factor of tissue
development in vitro and may improve the performance of engineered tissues in the body.
4.5 Concluding Remarks
This chapter has discussed three critical elements that define the mechanical microenvironment of a cell:
self-generated forces, counter forces from the ECM, and externally applied forces in the body. Extensive
work still needs to be done to create a coherent theory of mechanotransduction processes. At the cellular
level, the nature of the primary mechanosensor(s) remains to be a central question. In this regard,
investigations are limited by techniques that allow us to observe the force-induced changes in potential
mechanosensors at a subcellular length scale and in a miniature time-frame. At the tissue level, tissue-
scale responses to forces result from a dynamic and orchestrated interaction between different cell types
in a three-dimensional matrix environment. In most of the in vitro studies described here, mechanical
stimuli are imposed on monolayer cell cultures made of a single cell type. Although cultured cells sense
and respond to mechanical stimulation in this setting, it is not yet clear whether the same responses or
sensing mechanisms occur in vivo, but the wealth of in vitro data can guide in vivo experiments. Finally,
in the context of tissue engineering, it is important to understand how the physicality of scaffolds affects
cells, how the structure, composition, and mechanical properties of scaffolds may change as a result of
mikos: “9026_c004” — 2007/4/9 — 15:50 — page 13 — #13
Mechanical Forces on Cells 4-13
traction forces from the cells and the external forces from the body, and how scaffolds affect cells to sense
the external forces. These are just a few of the challenges for the future.
Acknowledgments
This work was supported by a Biomedical Engineering Research Grant from the Whitaker Foundation
(RG-02-0133). The author thanks Matthew Iwamoto, Cole Quam, In Suk Joung, and Deepa Mishra for
their help in manuscript preparation.
References
[1] Zhu, C., Bao, G., and Wang, N., Cell mechanics: mechanical responses, cell adhesion, and
molecular deformation, Annu. Rev. Biomed. Eng., 2, 189, 2000.
[2] Chen, C.S., Tan, J.L., and Tien, J., Mechanotransduction at cell–matrix and cell–cell contacts,
Annu. Rev. Biomed. Eng., 6, 3.1, 2004.
[3] Asthagiri, A.R. and Lauffenburger, D.A., Bioengineering models of cell signaling, Annu. Rev.
Biomed. Eng., 2, 31, 2000.
[4] Chicurel, M.E., Chen, C.S., and Ingber, D.E., Cellular control lies in the balance of forces, Curr.
Opin. Cell Biol., 10, 232, 1998.
[5] Katsumi, A. et al., Integrins in mechanotransduction, J. Biol. Chem., 279, 12001, 2004.
[6] Galbraith, C.G. and Sheetz, M.P., Forces on adhesive contacts affect cell function, Curr. Opin. Cell
Biol., 10, 566, 1998.
[7] Burridge, K. and Chrzanowska-Wodnicka, M., Focal adhesions, contractility, and signaling, Annu.
Rev. Cell Dev. Biol., 12, 463, 1996.
[8] Geiger, B. and Bershadsky, A., Exploring the neighborhood: adhesion-coupled cell mechano-
sensors, Cell, 110, 139, 2002.
[9] Geiger, B. and Bershadsky, A., Assembly and mechanosensory function of focal contacts, Curr.
Opin. Cell Biol., 13, 584, 2001.
[10] Ingber, D.E., Tensegrity I. Cell structure and hierarchical systems biology, J. Cell Sci., 116, 1157,
2003.
[11] Ingber, D.E., Mechanobiology and diseases of mechanotransduction, Ann. Med., 35, 564, 2003.
[12] Ingber, D.E., Tensegrity II. How structural networks influence cellular information processing
networks, J. Cell Sci., 116, 1397, 2003.
[13] Bershadsky, A.D., Balaban, N.Q., and Geiger, B., Adhesion-dependent cell mechanosensitivity,
Annu.Rev.CellDev.Biol., 19, 677, 2003.
[14] Narumiya, S., Ishizaki, T., and Watanabe, N., Rho effectors and reorganization of actin
cytoskeleton, FEBS Lett., 410, 68, 1997.
[15] Amano, M. et al., Phosphorylation and activation of myosin by Rho-associated kinase (Rho-
kinase), J. Biol. Chem., 271, 20246, 1996.
[16] Chrzanowska-Wodnicka, M. and Burridge, K., Rho-stimulated contractility drives the formation
of stress fibers and focal adhesions, J. Cell Biol., 133, 1403, 1996.
[17] Ridley, A.J. and Hall, A., The small GTP-binding protein rho regulates the assembly of focal
adhesions and actin stress fibers in response to growth factors, Cell, 70, 389, 1992.
[18] Zhong, C. et al., Rho-mediated contractility exposes a cryptic site in fibronectin and induces
fibronectin matrix assembly, J. Cell Biol., 141, 539, 1998.
[19] Harris, A.K., Wild, P., and Stopak, D., Silicone rubber substrata: a new wrinkle in the study of cell
locomotion, Science, 208, 177, 1980.
[20] Beningo, K.A., Lo, C.M., and Wang, Y.L., Flexible polyacrylamide substrata for the analysis of
mechanical interactions at cell–substratum adhesions, Meth. Cell Biol., 69, 325, 2002.
[21] Beningo, K.A. and Wang, Y.L., Flexible substrata for the detection of cellular traction forces, Trends
Cell Biol., 12, 79, 2002.
mikos: “9026_c004” — 2007/4/9 — 15:50 — page 14 — #14
4-14 Tissue Engineering
[22] Marganski, W.A., Dembo, M., and Wang, Y.L., Measurements of cell-generated deformations on
flexible substrata using correlation-based optical flow, Meth. Enzymol., 361, 197, 2003.
[23] Balaban, N.Q. et al., Force and focal adhesion assembly: a close relationship studied using elastic
micropatterned substrates, Nat. Cell Biol., 3, 466, 2001.
[24] Lauffenburger, D.A. and Horwitz, A.F., Cell migration: a physically integrated molecular process,
Cell, 84, 359, 1996.
[25] Beningo, K.A. et al., Nascent focal adhesions are responsible for the generation of strong propulsive
forces in migrating fibroblasts, J. Cell Biol., 153, 881, 2001.
[26] Wang, N. et al., Micropatterning tractional forces in living cells, Cell Motil. Cytoskeleton, 52, 97,
2002.
[27] Wang, N. et al., Mechanical behavior in living cells consistent with the tensegrity model, Proc. Natl
Acad. Sci. USA, 98, 7765, 2001.
[28] Stamenovic, D. et al., Effect of the cytoskeletal prestress on the mechanical impedance of cultured
airway smooth muscle cells, J. Appl. Physiol., 92, 1443, 2002.
[29] Brown, R.A. et al., Balanced mechanical forces and microtubule contribution to fibroblast
contraction, J. Cell Physiol., 169, 439, 1996.
[30] Dennerll, T.J. et al., Tension and compression in the cytoskeleton of PC-12 neurites. II: quantitative
measurements, J. Cell Biol., 107, 665, 1988.
[31] Ryan, P.L. et al., Tissue spreading on implantable substrates is a competitive outcome of cell–cell
vs. cell–substratum adhesivity, Proc. Natl Acad. Sci. USA, 98, 4323, 2001.
[32] Nelson, C.M. et al., Vascular endothelial-cadherin regulates cytoskeletal tension, cell spreading,
and focal adhesions by stimulating RhoA, Mol. Biol. Cell, 15, 2943, 2004.
[33] Silver, F.H. and Siperko, L.M., Mechanosensing and mechanochemical transduction: how is mech-
anical energy sensed and converted into chemical energy in an extracellular matrix? Crit. Rev.
Biomed. Eng., 31, 255, 2003.
[34] Miyamoto, S. et al., Integrin function: molecular hierarchies of cytoskeletal and signaling
molecules, J. Cell Biol., 131, 791, 1995.
[35] Miyamoto, S., Akiyama, S.K., and Yamada, K.M., Synergistic roles for receptor occupancy and
aggregation in integrin transmembrane function, Science, 267, 883, 1995.
[36] Ingber, D.E., Fibronectin controls capillary endothelial cell growth by modulating cell shape, Proc.
Natl Acad. Sci. USA, 87, 3579, 1990.
[37] Huang, S. and Ingber, D.E., The structural and mechanical complexity of cell-growth control, Nat.
Cell Biol., 1, E131, 1999.
[38] Chen, C.S. et al., Geometric control of cell life and death, Science, 276, 1425, 1997.
[39] Pelham, R.J., Jr. and Wang, Y., Cell locomotion and focal adhesions are regulated by substrate
flexibility, Proc. Natl Acad. Sci. USA, 94, 13661, 1997.
[40] Wang, H.B., Dembo, M., and Wang, Y.L., Substrate flexibility regulates growth and apoptosis of
normal but not transformed cells, Am. J. Physiol. Cell Physiol., 279, C1345, 2000.
[41] Halliday, N.L. and Tomasek, J.J., Mechanical properties of the extracellular matrix influence
fibronectin fibril assembly in vitro, Exp. Cell Res., 217, 109, 1995.
[42] Lo, C.M. et al., Cell movement is guided by the rigidity of the substrate, Biophys. J., 79, 144, 2000.
[43] Ingber, D.E., Mechanical signaling and the cellular response to extracellular matrix in angiogenesis
and cardiovascular physiology, Circ. Res., 91, 877, 2002.
[44] Geiger, B. et al., Transmembrane crosstalk between the extracellular matrix — cytoskeleton
crosstalk, Nat. Rev. Mol. Cell Biol., 2, 793, 2001.
[45] Millward-Sadler, S.J. and Salter, D.M., Integrin-dependent signal cascades in chondrocyte
mechanotransduction, Ann. Biomed. Eng., 32, 435, 2004.
[46] Bell, G.I., Models for the specific adhesion of cells to cells, Science, 200, 618, 1978.
[47] Ingber, D.E. and Folkman, J., Mechanochemical switching between growth and differentiation
during fibroblast growth factor-stimulated angiogenesis in vitro: role of extracellular matrix, J. Cell
Biol., 109, 317, 1989.
mikos: “9026_c004” — 2007/4/9 — 15:50 — page 15 — #15
Mechanical Forces on Cells 4-15
[48] Huang, S. and Ingber, D.E., Shape-dependent control of cell growth, differentiation, and apoptosis:
switching between attractors in cell regulatory networks, Exp. Cell Res., 261, 91, 2000.
[49] Huang, S., Chen, C.S., and Ingber, D.E., Control of cyclin D1, p27(Kip1), and cell cycle progression
in human capillary endothelial cells by cell shape and cytoskeletal tension, Mol. Biol. Cell, 9, 3179,
1998.
[50] Polte, T.R. et al., Extracellular matrix controls myosin light chain phosphorylation and cell con-
tractility through modulation of cell shape and cytoskeletal prestress, Am. J. Physiol. Cell Physiol.,
286, C518, 2004.
[51] McBeath, R. et al., Cell shape, cytoskeletal tension, and RhoA regulate stem cell lineage
commitment, Dev. Cell, 6, 483, 2004.
[52] Gooch, K.J. and Tennant, C.J., Mechanical Forces: Their Effects on Cells and Tissues, Springer-Verlag,
New York, 1997.
[53] Hamill, O.P. and Martinac, B., Molecular basis of mechanotransduction in living cells, Physiol.
Rev., 81, 685, 2001.
[54] Apodaca, G., Modulation of membrane traffic by mechanical stimuli, Am. J. Physiol. Renal Physiol.,
282, F179, 2002.
[55] Shieh, A.C. and Athanasiou, K.A., Principles of cell mechanics for cartilage tissue engineering,
Ann. Biomed. Eng., 31, 1, 2003.
[56] Davies, P.F., Flow-mediated endothelial mechanotransduction, Physiol. Rev., 75, 519, 1995.
[57] Bird, R.B., Stewart, W.E., and Lightfoot, E.N., Transport Phenomena, John Wiley & Sons, New
York, 1960.
[58] Schlichting, H., Boundary Layer Theory, McGraw-Hill, New York, 1979.
[59] Liu, S.Q., Yen, M., and Fung, Y.C., On measuring the third dimension of cultured endothelial cells
in shear flow, Proc. Natl Acad. Sci. USA, 91, 8782, 1994.
[60] Barbee, K.A., Davies, P.F., and Lal, R., Shear stress-induced reorganization of the surface
topography of living endothelial cells imaged by atomic force microscopy, Circ. Res., 74, 163,
1994.
[61] Barbee, K.A. et al., Subcellular distribution of shear stress at the surface of flow-aligned and
nonaligned endothelial monolayers, Am. J. Physiol., 268, H1765, 1995.
[62] Dewey, C.F., Jr. and DePaola, N. Exploring flow-cell interactions using computational fluid
dynamics, in Tissue Engineering, Woo, S.-L.Y. and Seguchi, Y. (Eds.), ASME, New York, 1989.
[63] Satcher, R.L., Jr. et al., The distribution of fluid forces on model arterial endothelium using
computational fluid dynamics, J. Biomech. Eng., 114, 309, 1992.
[64] Sakurai, A. et al., A computational fluid mechanical study of flow over cultured endothelial cells,
Adv. Bioeng., 20, 299, 1991.
[65] Yamaguchi, T.H. et al., Shear stress distribution over confluently cultured endothelial cells studied
by computational fluid dynamics, Adv. Bioeng., 20, 167, 1993.
[66] Papadaki, M. and McIntire, L.V. Quantitative measurement of shear-stress effects on endothelial
cells, in Methods in Molecular Medicine, Vol. 18: Tissue Engineering Methods and Protocols., Morgan,
J.R. and Yarmush, M.L. (Eds.), Humana Press, Totowa, NJ, 1998.
[67] Brown, T.D., Techniques for mechanical stimulation of cells in vitro:areview,J. Biomech., 33, 3,
2000.
[68] Haidekker, M.A., White, C.R., and Frangos, J.A., Analysis of temporal shear stress gradients during
the onset phase of flow over a backward-facing step, J. Biomech. Eng., 123, 455, 2001.
[69] Frangos, J.A., Huang, T.Y., and Clark, C.B., Steady shear and step changes in shear stimulate
endothelium via independent mechanisms — superposition of transient and sustained nitric
oxide production, Biochem. Biophys. Res. Commun., 224, 660, 1996.
[70] McKnight, N.L. and Frangos, J.A., Strain rate mechanotransduction in aligned human vascular
smooth muscle cells, Ann. Biomed. Eng., 31, 239, 2003.
[71] Clark, C.B., McKnight, N.L., and Frangos, J.A., Strain and strain rate activation of G proteins in
human endothelial cells, Biochem. Biophys. Res. Commun., 299, 258, 2002.
