Ferry M. Direct Stripcasting of Metals and Alloys: Processing, Microstructure and Properties
Подождите немного. Документ загружается.


Simulation
and
modelling
of
direct
strip
casting
243
Figure A.4 shows the computed transient heat flux profiles for the consecutive
immersion of a copper substrate into a stainless steel melt using temperature
measurements taken from optimised thermocouple positions within the
substrate
in
conjunction with a modified version of Beck's algorithm. The
figure highlights the reproducibility (accuracy) of the calculated heat flux
profile.
It
also shows that heat flux varies substantially during solidification
which indicates that a single value of
h (and
q)
is
an
unrealistic representation of
heat flow
in
processes such as
DSC.
Transient
heat
flux
calculations
for
a
moving
mould
The transient heat flux can also be calculated during DSC
but
is complicated
by
the fact that heat flux varies considerably
at
any given point
on
the mould
surface as it makes and breaks contact with the solidifying metal. Furthermore,
it is difficult to continually monitor the temperature within the mould (rolls or
belts) in these dynamic casting processes. Nevertheless, several workers have
made significant inroads into modelling of interfacial heat flux
in
single belt
casting (Guthrie
et
al.
2000),
single roll casting (Granasy
and
Ludwig
1991)
and
twin roll casting (Miyazawa
et
al.
1990;
Bradbury
and
Hunt
1995;
Guthrie
et
al.
2000).
Guthrie
and
co-workers
(2000)
were able to calculate the interfacial heat flux
during
DSC
by
monitoring temperature changes within the mould using
embedded thermocouples
and
incorporating a Langrangian coordinate system
moving
at
the same speed as both the mould
and
thermocouples. For vertical
TRC,
conduction in the angular
and
axial directions of the roll was regarded to
be negligible
and
Eq. 2.47 reduces
to:
pC
aT
=
[.!.~(rk
aT)]
Pat
rar
ar
(A.2)
where r is the radial position within the roll.
Similarly, for single belt strip casting, conduction
in
the casting
and
transverse
directions were assumed to be negligible and
Eq.
2.47 reduces to:
pC
aT
=~(k
aT)
Pat
ax ax
(A.3)
where x is the direction perpendicular to the moving belt.
Using appropriate boundary conditions
and
reliable thermophysical data, a
modified version of Beck's algorithm was used to calculate
h(t) for both casting
processes. A sample calculation is shown Figure 4.28 which demonstrates
clearly the time-dependence of interfacial heat flux during twin roll casting.

244
Direct
strip
casting
of
metals
and
alloys
A.3.2 Modelling of fluid flow
Mathematical models have also been developed for studying liquid flow fields in
the casting region of the strip caster. An understanding of
this phenomenon is
important since considerable flow of liquid metal occurs in the casting region of
the caster due to incoming flow from the nozzle and the movement of the mould.
These models are used for optimising nozzle design in many forms of strip
casting and may be tested using a water analogue of the strip casting process.
Despite the importance of fluid flow in
DSC,
very few modelling studies have
been reported in the open literature. Guthrie
and
Tavares
(1998)
used
computational fluid dynamics modelling to simulate 3-D turbulent flows, heat
transfer
and
solidification as molten metal is delivered into the mould of a
vertical
twin
roll caster. Their work demonstrated the significant influence of
nozzle design
in
TRC
on
velocity fields
and
temperature distribution
in
the melt
(see
e.g.
Figure
4.6).
A powerful method for capturing some of the essential features of fluid flow and
thermal phenomena in
DSC
is by combining models of fluid flow with those of
heat transfer. Some of the more sophisticated models take into account liquid
flow and plastic deformation and couple the thermal field with the velocity field.
For such models, however, it is necessary to make several simplifying
assumptions; one of the most notable being a constant interfacial heat transfer
coefficient.
A.3.3 Microstructural modelling
Microstructural evolution during
DSC
is notoriously difficult to predict since the
mechanisms of nucleation and growth of solidifying grains must be understood.
Furthermore, the process is dynamic and solidifying grains grow in response to
both the moving mould and thermal environment of the melt where substantial
liquid movement occurs and solute gradients are generated. There may also be
concomitant deformation during casting which may result in static and/or
dynamic restoration of the deformation microstructure.
Despite these challenges, semi-empirical modelling of
SDAS
as a function of heat
transfer conditions is possible by combining modified versions of Fourier's heat
flow equation with
Eq.
2.37
(see
e.g.
Loser
et
al.
(1993». Highly sophisticated
microstructural models have been devised by Rappaz and co-workers (see
e.g.
Takatani
et
al.
(2000»
by
combining cellular automata models with
2-D
and
3-D
finite element models. Based on various assumptions concerning the nucleation
kinetics and subsequent dendritic growth of columnar grains, together with the
effect of fluid flow
on
the solute field in the vicinity of growing dendrite tip,
CAFE
models are useful for predicting the effect of casting parameters (such as casting
speed in
TRC)
on
the final microstructure and texture of an alloy (see
e.g.
Figure
5.26).

Appendix B
Representation
of
Textures
and
their
Interpretation
B.t
Introduction
The individual crystallites in a material may be randomly oriented
or
aligned
in
a particular preferred crystallographic orientation. The
sum
of the
crystallographic orientations of the crystallites within a polycrystalline
aggregate is
known
as the
texture
of the material (Humphreys
and
Hatherly .
2004).
A texture
may
develop
by
processes such as electrodeposition, casting,
rolling, forging, extrusion, wire drawing
and
annealing. The particular type
and
strength of the texture is governed
both
by
the material (crystal structure,
phase distribution,
purity
etc.) as well as the processing route. Since many
aspects of the book are concerned
with
texture development
in
metals after
strip casting
and
further processing such as rolling, forming
or
heat treatment,
this appendix provides information required to
understand
and
interpret
textures. Further details of textures in materials
may
be found in Hatherly
and
Hutchinson
(1979),
Bunge
(1982),
Randle and Engler
(2000)
and
Humphreys
and
Hatherly
(2004).
B.2
Measurement of textures
The texture of a material can be measured
by
a range of techniques (Randle
and
Engler
2000;
Humphreys and Hatherly 2004). Macro-methods include X-ray
and
neutron diffraction
and
micro-methods include electron diffraction in
either the scanning
(SEM)
or
transmission electron microscope
(TEM)
using the
techniques of electron backscatter diffraction
(EBSD)
and
TEM microdiffraction.
The commonly used X-ray technique usually involves back reflection to
245

246
Direct
strip
casting
of
metals
and
alloys
generate a pole figure with the mathematical combination of several pole
figures required for more detailed texture information. A limitation of the
technique is the small volume of material examined
due
to the limited depth of
penetration
«
0.1
mm) of the X-ray beam into the sample. Furthermore, the
technique is of very limited use for micro-texture studies since the texture
generated is an average from a large number of crystallites.
Lens Polepi
Specimen
Data
analysis
and presentation
Diffraction pattern
on
phosphor screen
Figure B.l. Typical
EBSD
configuration in the
SEM
showing a typical Kikuchi pattern
impinging on a phosphor screen from a point on the sample, after Humphreys
and Hatherly
(2004)
(with kind permission of Elsevier Limited).
Electron
backscatter
diffraction
(EBSD)
The
EBSD
technique has developed over the past decade into a fully-automated
texture analysis facility (Randle and Engler
2000).
It
allows crystallographic
data to be generated in a microstructural framework for bulk (large) specimens
and utilises the automated computer analysis of
EBSD
patterns obtained from
the SEM to generate crystallographic data
on
a point-by-point basis over a
selected area of a sample. A typical
EBSD
setup is shown in Figure
B.1
which
comprises a sensitive camera and
an
image processing system for pattern
averaging and background subtraction. The acquisition software controls the
data acquisition, solves the diffraction patterns and stores the data. Additional
software analyses, manipulates and displays the data.
In
the technique, the electron beam of the
SEM
is focused
at
a point
on
the
surface of a highly tilted
(-60-70°) sample which results in backscattered
diffraction of electrons from that point (Figure
B.1).
The diffraction
phenomenon generates
an
EBSD
pattern
on
a phosphor screen
and
supplies all
the crystallographic information of that particular region of the sample. To
generate a
map
of the microstructure based
on
the information extracted from

Representation
of
textures
and
their
interpretation
247
the
EBSO
patterns, points
on
the sample are usually arranged in a regular grid
and
either the electron beam of the
SEM
steps to each
point
in
turn
or
the beam
is held stationary
and
the specimen stage traverses beneath it.
At
each step, the
coordinates of the point
and
crystallographic information are recorded and
stored using the acquisition software. From these data,
maps
revealing a range
of crystallographic features of the microstructure can be generated.
B.3
Representation
of
orientations and textures
The textures discussed
in
this book are produced by:
(i)
solidification
and
(ii)
rolling
and
annealing operations. The former are readily described with pole
figures
or
inverse pole figures
but
the latter are usually described
in
a more
sophisticated
way
since the major texture components of metal sheet produced
by
thermomechanical processing (TMP) are usually distributed as tubes of
orientation
or
fibres
in
three dimensional space. These textures are more easily
interpreted using the orientation distribution function
(OOF). The following
sections describe the main methods of representing the type of textures
encountered in this book
and
how
they are interpreted.
B.3.l Pole figures
A pole figure is a stereographic projection showing the distribution of poles of a
particular set of crystallographic planes in the assembly of crystallites (grains)
that constitutes the specimen (Humphreys
and
Hatherly 2004). To describe the
pole figure, one
or
more reference directions need to
be
assigned such as the
drawing direction in wire, the normal direction
(NO)
and
casting direction (CO)
or
rolling direction
(RO)
in strip produced
by
OSC
and
TMP, respectively.
Figure B.2a shows the distribution of
<001>
directions (i.e. poles of
{DOl}
planes)
of
an
arbitrarily-oriented grain in a cubic sample
with
respect to a set of
orthogonal external sample directions
D
1
,
D2
and
D
3
•
There are three
<001>
directions
per
grain
and
these project onto the surface of a reference sphere and,
by
viewing from
X,
the directions project back onto a 'projection' plane. Figure
B.2b
shows the projection plane of the
<001>
directions
with
respect to the
sample axes. As
an
example of nomenclature in sheet metal, a crystallite
oriented
with
[100]
direction parallel to NO (normal to
(100)
and
[001]
direction
parallel to
RO
gives the
(001)[001]
(cube) texture component. The orientation of
any grain
in
sheet/strip is usually represented as (hkl)[uvw] where the [uvw]
direction is contained in the
(hkl)
plane.
The pole figure of a
polycrystalline
material has a distribution of intensity which
may be represented either
by
individual points
on
the pole figure (for
microdiffraction techniques such as
EBSO
and
TEM)
or
contour lines
with
respect to a sample containing grains
with
a
random
distribution of

248
Direct
strip
casting
of
metals
and
alloys
orientations. Contoured pole figures can be generated both
by
global texture
analysis (X-ray or neutron diffraction) and discrete texture measurements
(EBSD).
•
Projection
plane
•
D1
I----=----j.:::....!.----j
D3
•
Figure
B.2.
(a)
Distribution
of
the three
<001>
directions in a
cubic
material
for
a grain
of
arbitrary orientation with respect
to
the external coordinate system and
(b) their projection onto a
reference
plane
to
generate the
001
pole figure
for
this particular grain.
A typical texture in a directionally solidified cubic metal is given in Figure
B.3
which shows the orientations of one hundred individual grains. Due to the
orthogonality of the specimen axes, CD is shown
at
the top of the pole figure
with ND and the transverse direction
(TO)
represented
at
the centre
and
edge of
the pole figure, respectively. This
001
pole figure shows a high density of
orientations near ND
but
a random distribution around the circumference of
the pole figure and indicates that many of the grains have one of their
<001>
directions aligned closely to ND of the strip. There is
no
preferred alignment of
orientations
in
either TO or CD which indicates that casting has generated a
strong
<001>/
/ND
fibre
texture.

Representation
of textures
and
their
interpretation
249
The foregoing examples were concerned
with
poles of
{DOl}
planes to generate
the
001
pole figure
but
the poles of other crystallographic planes (i.e. the four
poles of
{111}
planes
per
grain
in
a cubic material) can
be
used
to generate
111
or
higher
order
pole figures.
It
is important to note that the poles of a given
grain
in
a
001
or
111
pole figure are distributed differently.
CD
Figure
B.3.
001
pole figure of one
hundred
grain orientations
in
a cubic material
showing
an
ideal
<OOl>//ND
fibre typical texture
produced
by
directional solidification processes.
B.3.2 Inverse
pole
figures
The inverse pole figure is a useful
mode
of representing
the
texture generated
in processes that require the specification of only a single axis. This is suitable
for directional solidification as well as for axisymmetric deformation processes
such as wire
drawing
or
extrusion. The frequency
with
which a particular
crystallographic direction coincides
with
the specimen axis is plotted
in
a single
triangle of a stereo graphic projection.
NO
<001>
<111>
<111>
.-
:
••
•
••
e.
CD
.:.
:
•••
. . .
.-
e
••
.,
•••••
I.
••
••
•
• •
••
• •
• e
•••
,
.....
::.
..
..
.
...
..
."
. .
....
..-: .
<110> <001>
<110>
Figure
B.4.
ND
and
CD inverse pole figures showing the distribution of the grain
orientations given
in
Figure
B.3.
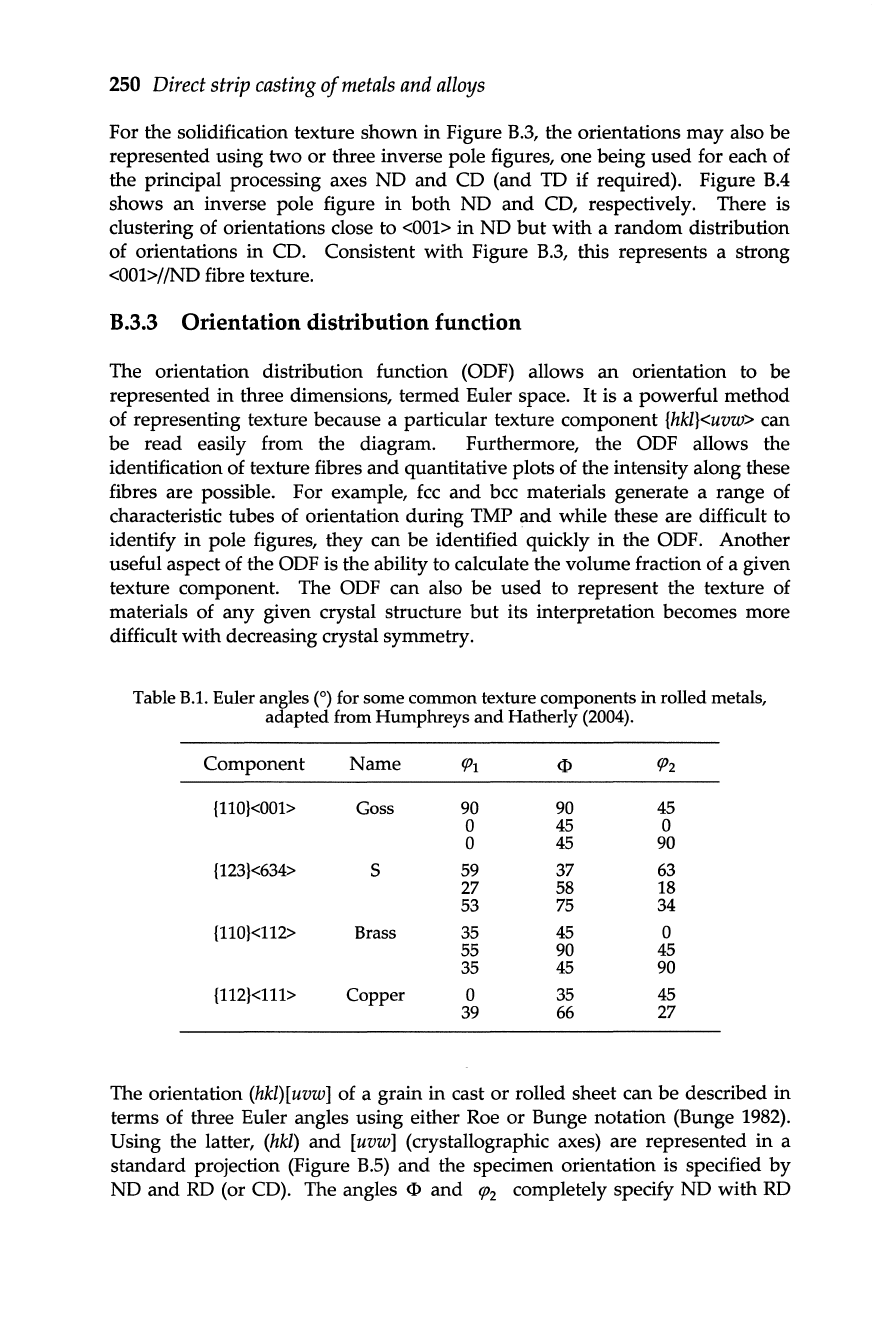
250
Direct
strip
casting
of
metals
and
alloys
For the solidification texture shown in Figure
B.3,
the orientations
may
also be
represented using two or three inverse pole figures, one being used for each of
the principal processing axes
NO
and
CO (and TO if required). Figure
B.4
shows
an
inverse pole figure in both NO
and
CO, respectively. There is
clustering of orientations close to
<001>
in
NO
but
with
a
random
distribution
of orientations in
CO. Consistent
with
Figure
B.3,
this represents a strong
<001>/
/NO fibre texture.
B.3.3
Orientation distribution function
The orientation distribution function (OOF) allows
an
orientation to be
represented in three dimensions, termed Euler space.
It
is a powerful method
of representing texture because a particular texture component
{hkl}<uvw> can
be read easily from the diagram. Furthermore, the
OOF allows the
identification of texture fibres
and
quantitative plots of the intensity along these
fibres are possible. For example,
fcc
and
bcc materials generate a range of
characteristic tubes of orientation during TMP
and
while these are difficult to
identify in pole figures, they can be identified quickly in the
OOF. Another
useful aspect of the
OOF is the ability to calculate the volume fraction of a given
texture component. The
OOF can also be used to represent the texture of
materials of any given crystal structure
but
its interpretation becomes more
difficult
with
decreasing crystal symmetry.
Table
B.l. Euler angles
(0)
for
some common texture components
in
rolled metals,
adapted
from
Humphreys and Hatherly
(2004).
Component Name
IPl
<l>
1P2
{1l0}<001>
Goss
90 90
45
0
45
0
0
45
90
{123}<634>
5
59
37
63
27
58
18
53
75
34
{1l0}<1l2>
Brass
35
45
0
55
90
45
35
45
90
{1l2}<1l1>
Copper 0
35
45
39
66
27
The orientation (hkl)[uvw] of a grain in cast
or
rolled sheet can be described in
terms of three Euler angles using either Roe or Bunge notation (Bunge 1982).
Using the latter,
(hkl)
and
[uvw] (crystallographic axes) are represented in a
standard projection (Figure
B.5)
and
the specimen orientation is specified
by
NO
and
RO
(or CO). The angles
<l>
and
1P2
completely specify NO
with
RO

Representation
of
textures
and
their
interpretation
251
lying
in
the plane normal to NO. The angle
CPl
therefore completely specifies
RD.
The orientation of the grain can be displayed
in
3-D
with
the Euler angles
as axes. For cubic materials, the orientation is completely represented within a
90
x
90
x
90"
volume of Euler space. The advantage of the OOF over pole figures
is that a given texture component is completely described
by
the set of Euler
angles:
<l>,
CPl
and
CP2'
A family of texture components, {hkl}<uvw>, gives
several sets of Euler angles, Table
B.1.
It
is useful to note
that
mathematical
relationships exist for converting between Miller Indices
and
Euler angles
(Bunge 1982).
100
//<:~
001
r---~----~~--------~010
<I>
~ND
....
....•...•......
Figure
B.s.
Definition of Euler angles in cubic materials with respect to the standard
<001>
projection, after Humphreys and Hatherly
(2004)
(with kind
permission
of
Elsevier Limited).
The OOF
data
of rolled
fcc
metals are normally represented as a series of slices
taken
through
Euler space
at
CP2
=
0,
5,
10
...
90°.
This is a result of the
deformation texture usually consisting of a tube of orientations, called the
,B-fibre,
which runs through Euler space from {1l0}<1l2> (Brass orientation) through
{123}<634>
(5
orientation) to {1l2}<1l1> (Copper orientation) (Humphreys
and
Hatherly
2004).
Another important orientation tube
in
fcc
metals is the lXfcc-fibre
which runs from {1l0}<1l2> to
{llO}<OO1>
(Goss orientation). Figure
B.6
is a
schematic representation of one of the branches of
both
the a
fcc
-
and
j3
-fibres
in
Euler space. For rolled (and annealed) bcc metals,
much
of the important
crystallographic information is found within the
CP2
= 45° section of the OOF.
This is illustrated
in
Figure
B.7
which shows the classic a-fibre «Oll>//RO)
and
r-fibre «l11>//NO) as well as some other
important
texture components
featured
in
this book. There are other orientation tubes of lesser importance for
metals based
on
either type of crystal structure
and
these are described elsewhere
(Bunge
1982;
Humphreys
and
Hatherly
2004).

252
Direct
strip
casting
of
metals
and
alloys
</>1
90·
~--+---~------------~
Figure
B.6.
90
x
90
x 90° volume of Euler space showing the
arcc·
and
,B-fibres
that
develop
in
rolled
fcc
materials, after Hirsch
and
Lucke (1988)
(with
kind
permission of Elsevier Limited).
o.e-----:::----==::~_4_;.--:'
_<i>
__
1
______
~_90·
(001
)[110]
(001
)[010]
(001
)[110]
I
ru-fibre
<I>
(223)[110]
r
'Y-fibre
(111)[112]
(111)[110]
(11'1)[121]
(111)[011]
~
(554)[225]
,90.
(110)[110]
(110)[001]
Figure
B.7.
rp2
= 45° section of Euler space showing the location of important texture
components
in
rolled bcc materials, after Hutchinson
and
Ryde (1997).
