Федосеев В.В. и др. Экономико-математические методы и прикладные модели

Подождите немного. Документ загружается.

Эконометрические модели

281

№

филиала

Производитель-

ность труда (у)

Фондововоору-

женность (Xj)

Энерговооружен-

ность (х

)

1 74 33 56

2 84 34 58

3 73 36 67

4 93 35 70

5 56 33 73

6 71 37 77

7 117 39 78

8 111 42 99

9 135 43 93

10 125 44 96

Требуется:

1) рассчитать парные коэффициенты корреляции и пояснить

их экономический смысл;

2) найти коэффициент множественной корреляции и со-

вокупный коэффициент детерминации и охарактеризовать

степень совместного влияния факторов фондовооруженности

и энерговооруженности на производительность труда;

3) построить модель множественной линейной регрессии

производительности труда от факторов фондо- и энерговоору-

женности;

4) рассчитать частные коэффициенты корреляции, детер-

минации, эластичности и частные бета-коэффициенты и с их

помощью оценить влияние отдельных факторов (при неиз-

менном значении других).

ГЛАВА 8

НЕКОТОРЫЕ ПРИКЛАДНЫЕ МОДЕЛИ

ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ

• Моделирование спроса и потребления

• Модели управления запасами

• Моделирование систем массового обслуживания

• Элементы теории игр в задачах моделирования экономических

процессов

8.1.

Моделирование спроса и потребления

Целевая функция потребления и моделирование

поведения потребителей

В условиях рыночной системы управления производст-

венной и сбытовой деятельностью предприятий и фирм в

основе принятия хозяйственных решений лежит рыночная

информация, а обоснованность решений проверяется рын-

ком в ходе реализации товаров и услуг. При таком подходе

начальным пунктом всего цикла предпринимательской дея-

тельности становится изучение потребительского спроса.

Рассмотрим некоторые вопросы моделирования спроса и по-

требления.

Уровень удовлетворения материальных потребностей об-

щества (уровень потребления) можно выразить целевой

функцией потребления U = U(Y), где вектор переменных

0 включает разнообразные виды товаров и услуг. Ряд

свойств этой функции удобно изучать, используя геометри-

ческую интерпретацию уравнений U(Y) = С, где С — ме-

няющийся параметр, характеризующий значение (уровень)

целевой функции потребления; в качестве величины С мо-

жет выступать, например, доход или уровень материального

благосостояния.

Некоторые прикладные модели экономических

процессов

283

В пространстве потребительских благ каждому уравнению

U(Y) = С соответствует определенная поверхность равноцен-

ных, или безразличных, наборов благ, которая называется

поверхностью безразличия. Для наглядности рассмотрим

пространство двух благ, например, в виде двух агрегирован-

ных групп товаров: продукты питания (i/i) и непродовольст-

венные товары, включая услуги (j/г)- Тогда уровни целевой

функции потребления можно изобразить на плоскости в ви-

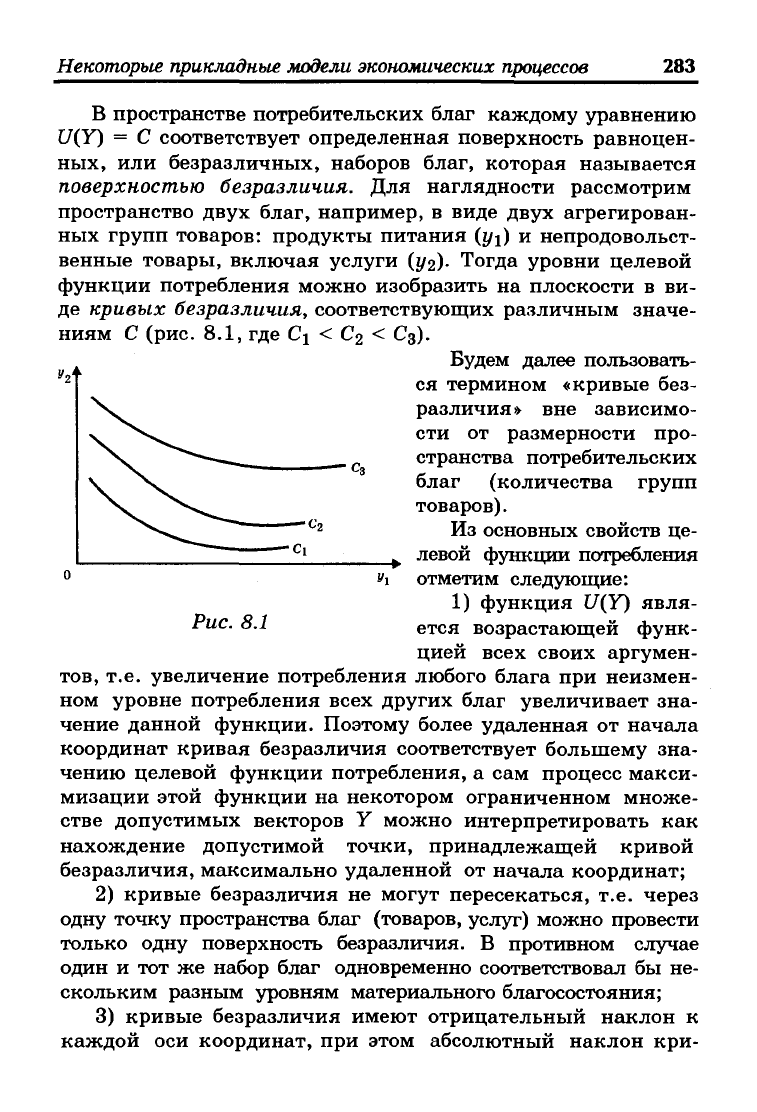
де кривых безразличия, соответствующих различным значе-

ниям С (рис. 8.1, где С\ < С2 < Сз).

Будем далее пользовать-

ся термином «кривые без-

различия» вне зависимо-

сти от размерности про-

странства потребительских

благ (количества групп

товаров).

Из основных свойств це-

^ левой функции потребления

отметим следующие:

1) функция U(Y) явля-

ется возрастающей функ-

цией всех своих аргумен-

тов,

т.е. увеличение потребления любого блага при неизмен-

ном уровне потребления всех других благ увеличивает зна-

чение данной функции. Поэтому более удаленная от начала

координат кривая безразличия соответствует большему зна-

чению целевой функции потребления, а сам процесс макси-

мизации этой функции на некотором ограниченном множе-

стве допустимых векторов У можно интерпретировать как

нахождение допустимой точки, принадлежащей кривой

безразличия, максимально удаленной от начала координат;

2) кривые безразличия не могут пересекаться, т.е. через

одну точку пространства благ (товаров, услуг) можно провести

только одну поверхность безразличия. В противном случае

один и тот же набор благ одновременно соответствовал бы не-

скольким разным уровням материального благосостояния;

3) кривые безразличия имеют отрицательный наклон к

каждой оси координат, при этом абсолютный наклон кри-

284

Глава 8

вых уменьшается при движении в положительном направ-

лении по каждой оси, т.е. кривые безразличия являются

выпуклыми кривыми.

Методы построения целевой функции потребления осно-

ваны на обобщении опыта поведения потребителей и тен-

денций покупательского спроса в зависимости от уровня

благосостояния. В качестве примера приведем квадратич-

ную целевую функцию потребления для трех агрегирован-

ных групп товаров, построенную на основе обработки дан-

ных бюджетной статистики:

U(Y) = (1 -

1,841а)

У1

+ (1 - 2,054a)j/

+ (1 - 2,116а)у

+ 0,668- lO-V +

1,230-Ю-^ц/з

1,234-Ю-^уз

+ 0,506

•

Ю-

j/f + 1,104

•

10-*у

Уз + 0,492

•

10~

у\ ,

где параметр а означает число детей в семье, у у — потребле-

ние продуктов питания,

y<i

— потребление промышленных

товаров, г/з — потребление платных услуг (в стоимостном

выражении).

Перейдем к вопросу моделирования поведения потреби-

телей в условиях товарно-денежных отношений на базе це-

левой функции потребления. В основе модели поведения

потребителей лежит гипотеза, что потребители, осуществляя

выбор товаров при установленных ценах и имеющемся доходе,

стремятся максимизировать уровень удовлетворения своих

потребностей.

Пусть в пространстве п видов товаров исследуется пове-

дение совокупности потребителей. Обозначим спрос потре-

бителей через вектор У = {у\,

у%,...,

), а цены на различ-

ные товары — через вектор Р = (pi,

Р2>--->

Рп)-

При величине

дохода D потребители могут выбирать только такие комби-

нации товаров, которые удовлетворяют бюджетному

ограничению2\piVi ^ D. Предположим, что предпочтение по-

i=l

требителей на множестве товаров выражается целевой

функцией потребления U(Y). Тогда простейшая модель по-

ведения потребителей в векторной форме записи будет

иметь вид:

Некоторые прикладные модели экономических

процессов

285

U(Y) -> max;

PY<D;

(8.1)

Рис. 8.2

Y>0.

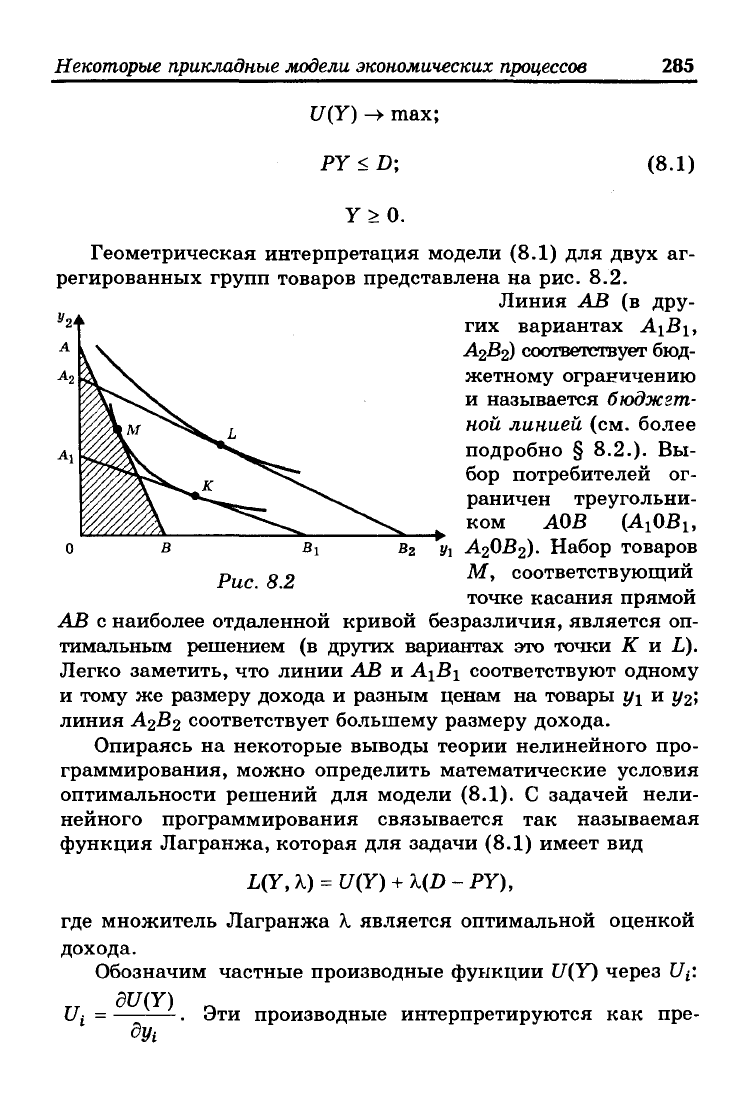
Геометрическая интерпретация модели (8.1) для двух аг-

регированных групп товаров представлена на рис. 8.2.

Линия АВ (в дру-

гих вариантах А\В\,

А2В2) соответствует бюд-

жетному ограничению

и называется бюджгт-

ной линией (см. более

подробно § 8.2.). Вы-

бор потребителей ог-

раничен треугольни-

ком АОВ (AjOBi,

^у

А2ОВ2). Набор товаров

М, соответствующий

точке касания прямой

АВ с наиболее отдаленной кривой безразличия, является оп-

тимальным решением (в других вариантах это точки К и L).

Легко заметить, что линии АВ и А\В\ соответствуют одному

и тому же размеру дохода и разным ценам на товары у\ и у2\

линия А2В2 соответствует большему размеру дохода.

Опираясь на некоторые выводы теории нелинейного про-

граммирования, можно определить математические условия

оптимальности решений для модели (8.1). С задачей нели-

нейного программирования связывается так называемая

функция Лагранжа, которая для задачи (8.1) имеет вид

L(Y,

= U(Y)

X(D - PY),

где множитель Лагранжа X является оптимальной оценкой

дохода.

Обозначим частные производные функции U(Y) через 17^:

dU(Y)

Эти производные интерпретируются как пре-

286

Глава 8

дельные полезные эффекты {предельные полезности) соот-

ветствующих потребительских благ и характеризуют при-

рост целевой функции потребления при увеличении исполь-

зования i-ro блага (товара) на некоторую условную «малую

единицу».

Необходимыми условиями того, что вектор Y

будет оп-

тимальным решением, являются условия Куна—Таккера:

ЩТГ°) < X°

; i = Ъп,

при этом

Ui(Y°) = X°pi , если j/f > 0 (товар приобретается), (8.2)

U£Y°) < X°pi , если j/j = 0 (товар не приобретается),

РУ° = £>.

Последнее из соотношений (8.2) соответствует полному

использованию дохода, и для этого случая очевидно нера-

венство X.

> 0.

Из условий оптимальности (8.2) следует, что

Щ^-х», tf»o.

Это означает, что потребители должны выбирать товары

таким образом, чтобы отношение предельной полезности к

цене товара было одинаковым для всех приобретаемых то-

варов. Другими словами, в оптимальном наборе предельные

полезности выбираемых товаров должны быть пропорцио-

нальны ценам.

Функции покупательского спроса

Функциями покупательского спроса (далее будем назы-

вать их просто функциями спроса) называются функции, от-

ражающие зависимость объема спроса на отдельные товары

и услуги от комплекса факторов, влияющих на него. Такие

функции применяются в аналитических моделях спроса и

потребления и строятся на основе информации о структуре

доходов населения, ценах на товары, составе семей и других

факторах. Рассмотрим построение функций спроса в зави-

симости от двух факторов — дохода и цен.

Некоторые прикладные модели экономических

процессов

287

Пусть в модели (8.1) цены и доход рассматриваются как

меняющиеся параметры. Переменную дохода будем обозначать Z.

Тогда решением оптимизационной задачи (8.1) будет век-

торная функция Y° = Y°(P,Z), компонентами которой явля-

ются функции спроса на определенный товар от цен и дохода:

y?=f

(P,Z).

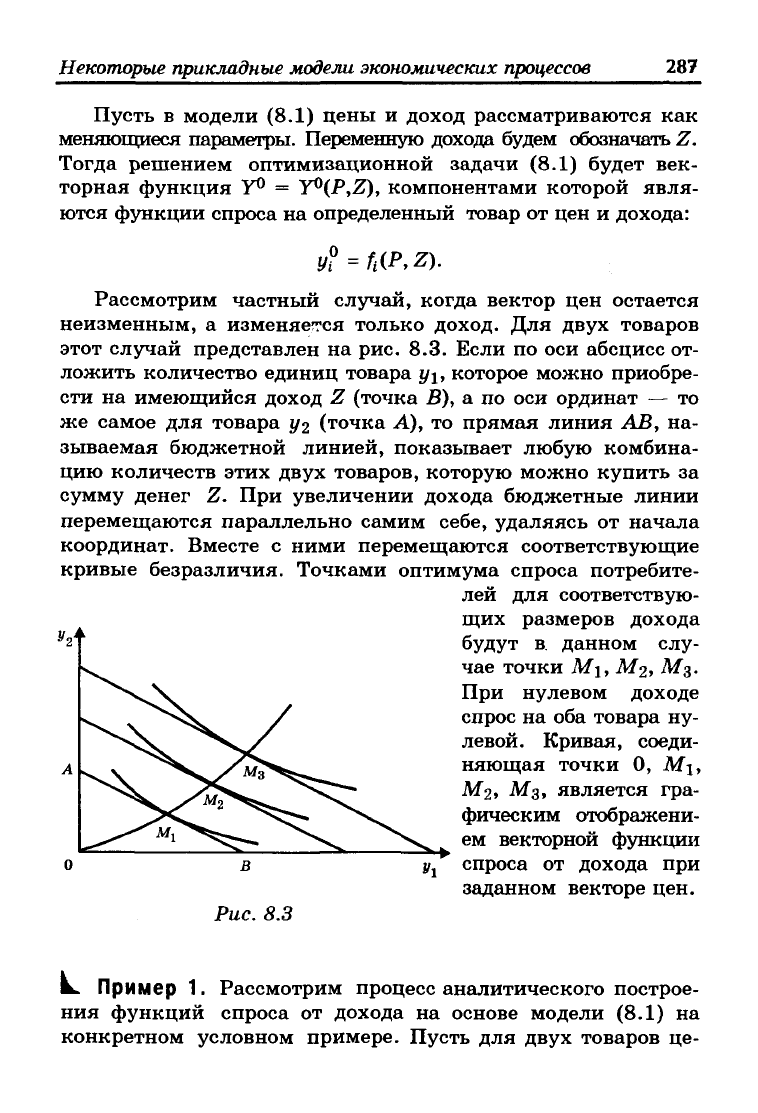
Рассмотрим частный случай, когда вектор цен остается

неизменным, а изменяется только доход. Для двух товаров

этот случай представлен на рис. 8.3. Если по оси абсцисс от-

ложить количество единиц товара у\, которое можно приобре-

сти на имеющийся доход Z (точка В), а по оси ординат — то

же самое для товара j/2 (точка Л), то прямая линия АВ, на-

зываемая бюджетной линией, показывает любую комбина-

цию количеств этих двух товаров, которую можно купить за

сумму денег Z. При увеличении дохода бюджетные линии

перемещаются параллельно самим себе, удаляясь от начала

координат. Вместе с ними перемещаются соответствующие

кривые безразличия. Точками оптимума спроса потребите-

лей для соответствую-

щих размеров дохода

будут в данном слу-

чае точки М\, М2, М3.

При нулевом доходе

спрос на оба товара ну-

левой. Кривая, соеди-

няющая точки 0, М\,

Л^2> Л^з> является гра-

фическим отображени-

ем векторной функции

спроса от дохода при

заданном векторе цен.

Рис. 8.3

к. Пример 1. Рассмотрим процесс аналитического построе-

ния функций спроса от дохода на основе модели (8.1) на

конкретном условном примере. Пусть для двух товаров це-

288

Глава 8

левая функция потребления имеет вид U(Y) = у\У

вектор

цен равен Р = (3; 6); величина дохода равна Z. Так как в

данном случае предельные полезности имеют вид:

ду\ ду

то необходимые условия оптимума (8.2) дают следующую

систему уравнений (X — множитель Лагранжа):

у\

гх-,

3z/i +

%у

= Z.

После подстановки первого уравнения во второе получим

Зу1у

= 2у

• Выразив из третьего уравнения 3i/i и подставив

в последнее равенство, будем иметь (Z - 6у

)у

= 2у

, откуда

можно получить, что у

= 1/8 Z. Подставив этот результат в

третье уравнение, получим у\ = 1/12 Z. Таким образом, для

данного примера функции спроса на товары у\ и у

от дохода

Z имеют вид:

У1

= 1/12 Z; у

=1/8 Z. J

Однофакторные функции спроса от дохода широко при-

меняются при анализе покупательского спроса. Соответст-

вующие этим функциям кривые y

= f

(Z) называются кри-

выми Энгеля (по имени изучавшего их немецкого экономиста).

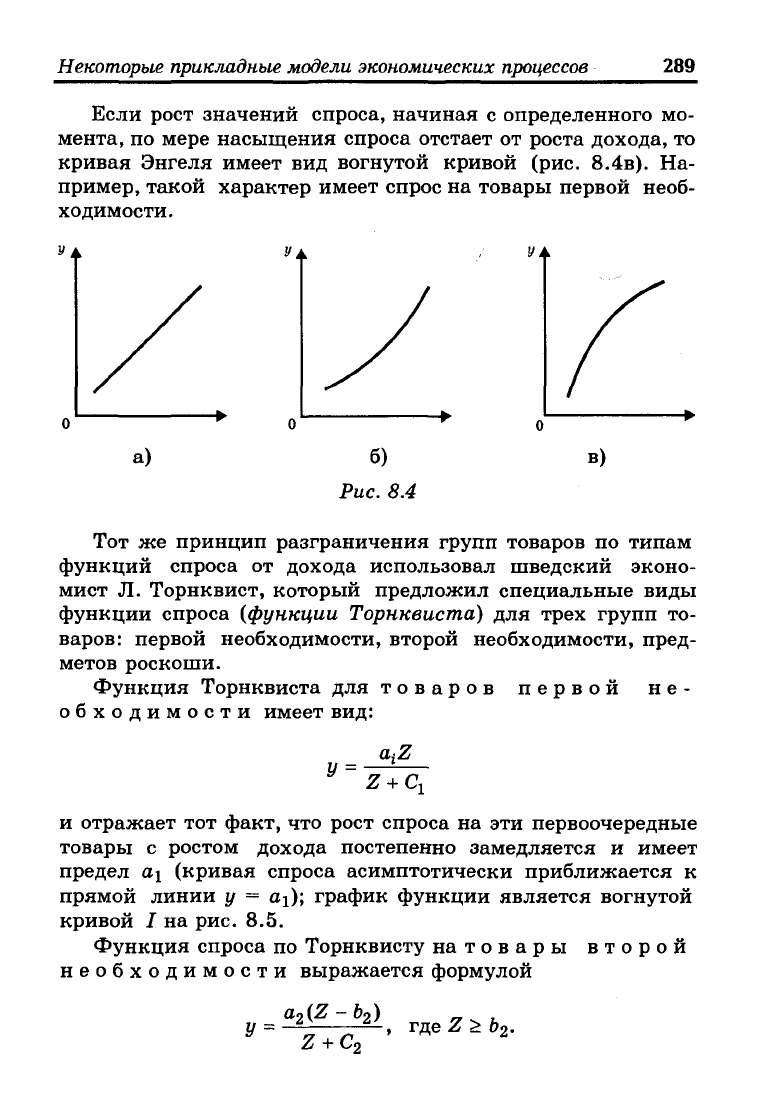
Формы этих кривых для различных товаров могут быть раз-

личны. Если спрос на данный товар возрастает примерно

пропорционально доходу, то функция будет линейной, как в

рассмотренном выше примере. Такой характер имеет, на-

пример, спрос на одежду, фрукты и др. Кривая Энгеля для

этого случая представлена на рис. 8.4а.

Если по мере роста дохода спрос на данную группу товаров

возрастает все более высокими темпами, то кривая Энгеля

будет выпуклой (рис. 8.46). Так ведет себя спрос на предме-

ты роскоши.

Некоторые прикладные модели экономических

процессов

289

Если рост значений спроса, начиная с определенного мо-

мента, по мере насыщения спроса отстает от роста дохода, то

кривая Энгеля имеет вид вогнутой кривой (рис. 8.4в). На-

пример, такой характер имеет спрос на товары первой необ-

ходимости.

а) б)

Рис. 8.4

в)

Тот же принцип разграничения групп товаров по типам

функций спроса от дохода использовал шведский эконо-

мист Л. Торнквист, который предложил специальные виды

функции спроса (функции Торнквиста) для трех групп то-

варов: первой необходимости, второй необходимости, пред-

метов роскоши.

Функция Торнквиста для товаров первой не-

обходимости имеет вид:

У =

и отражает тот факт, что рост спроса на эти первоочередные

товары с ростом дохода постепенно замедляется и имеет

предел ai (кривая спроса асимптотически приближается к

прямой линии у = а{); график функции является вогнутой

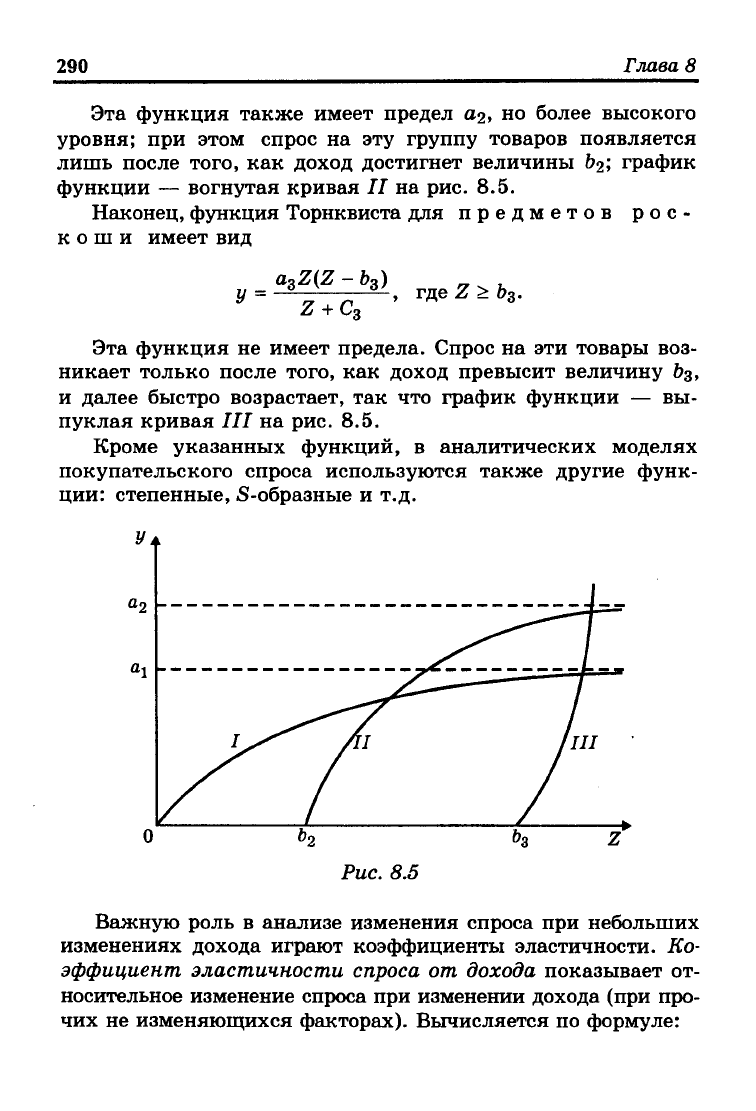
кривой I на рис. 8.5.

Функция спроса по Торнквисту на товары второй

необходимости выражается формулой

(

где Z

290

Глава 8

Эта функция также имеет предел

a<i,

но более высокого

уровня; при этом спрос на эту группу товаров появляется

лишь после того, как доход достигнет величины Ь^; график

функции — вогнутая кривая II на рис. 8.5.

Наконец, функция Торнквиста для предметов рос-

коши имеет вид

aoZ(Z -bo) „ ,_

Эта функция не имеет предела. Спрос на эти товары воз-

никает только после того, как доход превысит величину &з>

и далее быстро возрастает, так что график функции — вы-

пуклая кривая III на рис. 8.5.

Кроме указанных функций, в аналитических моделях

покупательского спроса используются также другие функ-

ции: степенные, S-образные и т.д.

0 Ь

Рис. 8.5

Важную роль в анализе изменения спроса при небольших

изменениях дохода играют коэффициенты эластичности. Ко-

эффициент эластичности спроса от дохода показывает от-

носительное изменение спроса при изменении дохода (при про-

чих не изменяющихся факторах). Вычисляется по формуле: