Федосеев В.В. и др. Экономико-математические методы и прикладные модели

Подождите немного. Документ загружается.

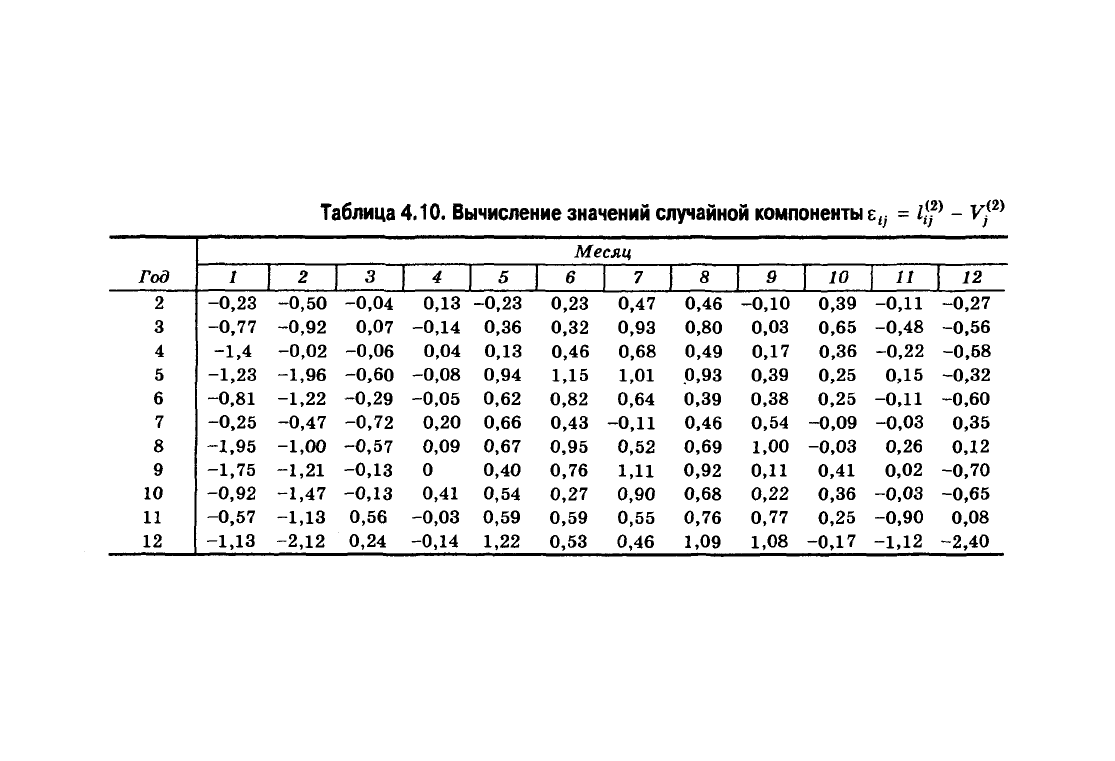
Таблица 4.10. Вычисление значений случайной компоненты z

= l-f

}

- F

;

<2)

Год

-0,23

-0,77

-1,4

-1,23

-0,81

-0,25

-1,95

-1,75

-0,92

-0,57

-1,13

-0,50

-0,92

-0,02

-1,96

-1,22

-0,47

-1,00

-1,21

-1,47

-1,13

-2,12

-0,04

0,07

-0,06

-0,60

-0,29

-0,72

-0,57

-0,13

0,56

0,24

0,13

-0,14

0,04

-0,08

-0,05

0,20

0,09

0,41

-0,03

-0,14

-0,23

0,36

0,13

0,94

0,62

0,66

0,67

0,40

0,54

0,59

1,22

Месяц

0,23

0,32

0,46

1,15

0,82

0,43

0,95

0,76

0,27

0,59

0,53

0,47

0,93

0,68

1,01

0,64

-0,11

0,52

1,11

0,90

0,55

0,46

0,80

0,49

0,93

0,39

0,46

0,69

0,92

0,68

0,76

1,09

-0,10

0,03

0,17

0,39

0,38

0,54

1,00

0,11

0,22

0,77

1,08

0,39

0,65

0,36

0,25

-0,09

-0,03

0,41

0,36

0,25

-0,17

-0,11

-0,48

-0,22

0,15

-0,11

-0,03

0,26

0,02

-0,03

-0,90

-1,12

-0,27

-0,56

-0,58

-0,32

-0,60

0,35

0,12

-0,70

-0,65

0,08

-2,40

182

Глава 4

14%

_ti

определяем величины коэффициента напряженности Ki для

каждого года, кроме первого и последнего. Для первого и

последнего годов значение коэффициента напряженности не

вычисляются, так как после повторного сглаживания в них ос-

талось лишь по четыре наблюдения, и их использование иска-

жает при расчетах средние характеристики всего ряда.

Значения коэффициента напряженности сезонной волны:

3,02

2,47

2,44

2,09

2,48

2,41

2,10

2,34

2,08

1,79

8. Используя коэффициент напряженности K

вычисляем

окончательные значения сезонной компоненты временного

ряда (табл. 4.11): V

= v\

•

. J

Перейдем к рассмотрению статистических методов оценки

уровня сезонности. До сих пор мы в основном использовали

аддитивное представление модели сезонного временного ряда

(4.19).

Однако не менее разумной, как считают многие спе-

циалисты, является и мультипликативная модель:

=Щ1

}

+в

(4.40)

где U

j — «годовая» составляющая (тренд);

Ij — постоянная пропорциональности для /-го месяца

(квартала), не меняющаяся от года к году.

Поскольку постоянная пропорциональности безразмер-

ная и не меняется от года к году, то ее можно использовать

для определения уровня сезонности во временном ряду.

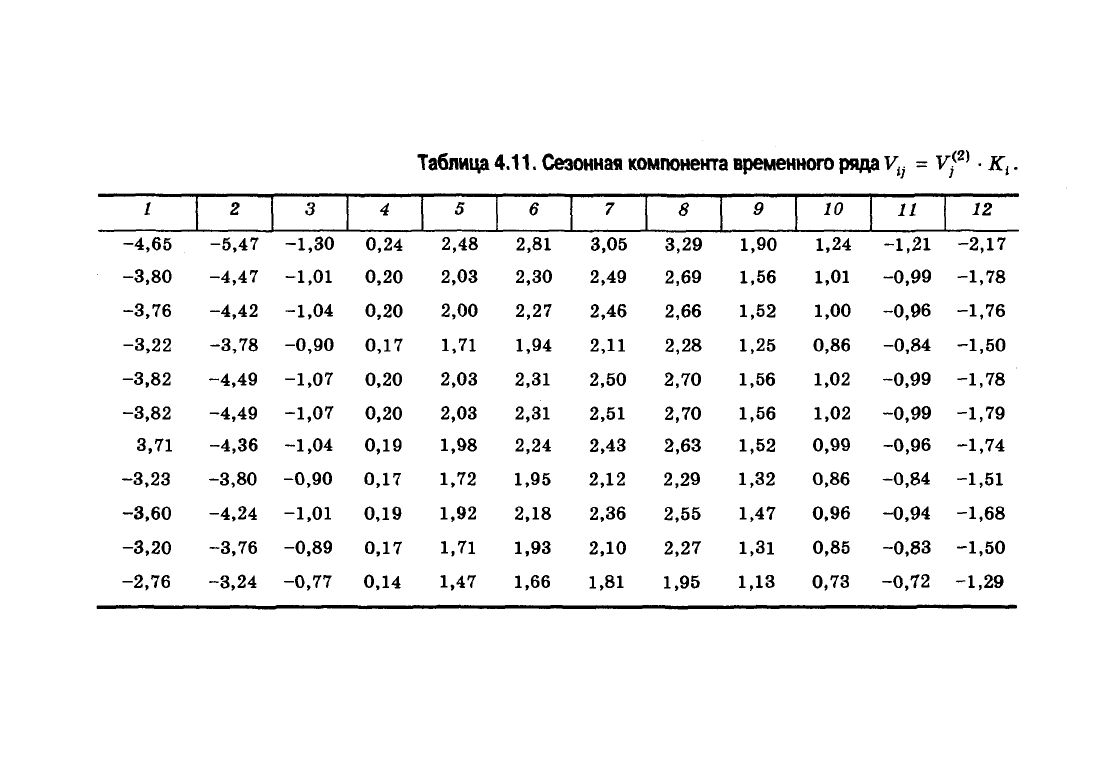
Таблица

4.11.

Сезонная компонента временного ряда V

= vf* • K

-4,65

-3,80

-3,76

-3,22

-3,82

3,71

-3,23

-3,60

-3,20

-2,76

-5,47

-4,47

-4,42

-3,78

-4,49

-4,36

-3,80

-4,24

-3,76

-3,24

-1,30

-1,01

-1,04

-0,90

-1,07

-1,04

-0,90

-1,01

-0,89

-0,77

0,24

0,20

0,17

0,20

0,19

0,17

0,19

0,17

0,14

2,48

2,03

2,00

1,71

2,03

1,98

1,72

1,92

1,71

1,47

2,81

2,30

2,27

1,94

2,31

2,24

1,95

2,18

1,93

1,66

3,05

2,49

2,46

2,11

2,50

2,51

2,43

2,12

2,36

2,10

1,81

3,29

2,69

2,66

2,28

2,70

2,63

2,29

2,55

2,27

1,95

1,90

1,56

1,52

1,25

1,56

1,52

1,32

1,47

1,31

1,13

1,24

1,01

1,00

0,86

1,02

0,99

0,86

0,96

0,85

0,73

-1,21

-0,99

-0,96

-0,84

-0,99

-0,96

-0,84

-0,94

-0,83

-0,72

-2,17

-1,78

-1,76

-1,50

-1,78

-1,79

-1,74

-1,51

-1,68

-1,50

-1,29

184 Глава 4

Приближенные оценки коэффициентов пропорциональ-

ности могут быть получены следующим образом

/;=^—,

(4.41)

где

2>„

Если известны значения тренда U

j и сезонной компо-

ненты V

j в аддитивной модели, то I

j можно оценить и бо-

лее точно:

V,, Y

1ц=-^—У---Д. (4.43)

' Щ Щ

Последнее говорит о возможности оценки уровня сезон-

ности независимо от того, какая рассматривается модель:

(4.19) или (4.40). Оценки /

;

по формуле (4.41) иногда назы-

вают еще индексами сезонности.

Чаще, однако, рассматривают не просто ряд из относи-

тельных величин Ij, а ряд процентов:

Ij=^

100%. (4.44)

Из (4.44) с учетом (4.43) можно заключить, что индексы

сезонности Ij характеризуют степень отклонения уровня се-

зонного временного ряда от ряда средних Yi (тренда) или,

иначе говоря, степень колеблемости относительно 100%, так

как если Y

—

Uij, то Ij =100%.

Методы и модели анализа динамики экономических

процессов

185

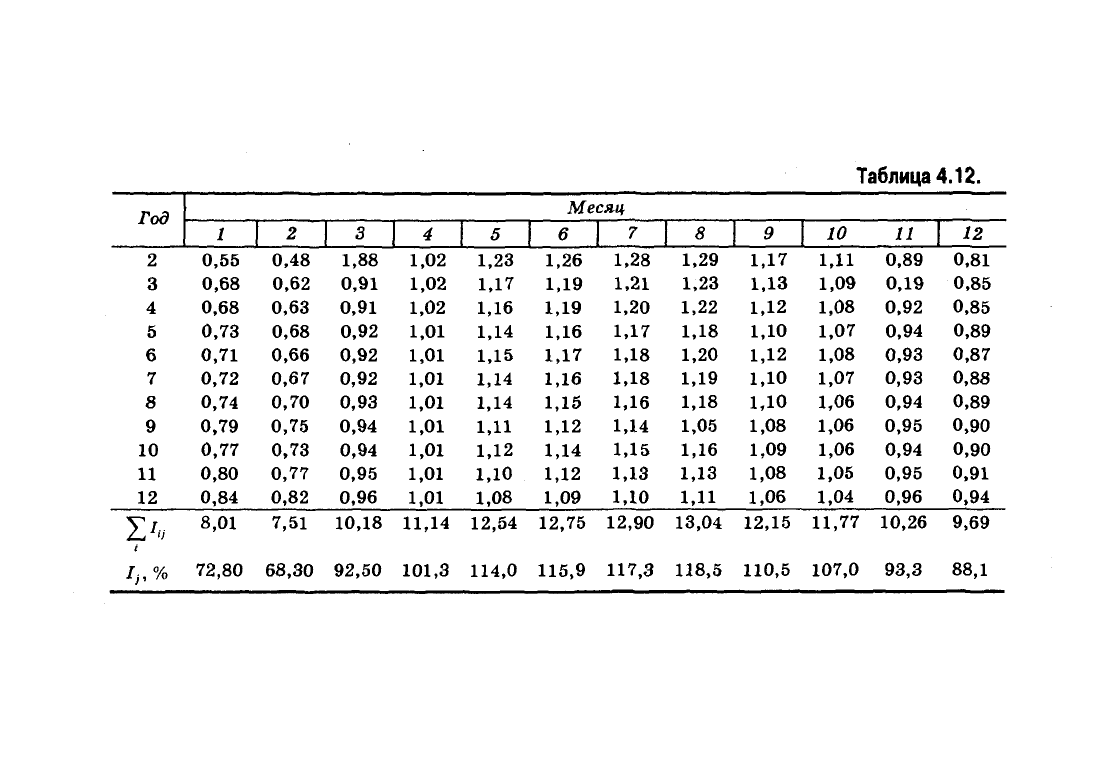
к. Пример 2. Найдем оценки уровня сезонности временно-

го ряда, представленного в табл. 4.6, через индексы сезонно-

сти,

проводя расчет 1ц по формуле (4.43). Для этого восполь-

зуемся табл. 4.9, 4.11, в которых приведены значения трен-

да U\- и сезонной компоненты Уц. В результате получим

табл. 4.12, состоящую из коэффициентов 1ц.

В предпоследней строке табл. 4.12 приведены суммы 1ц

по столбцам, в последней строке — индексы сезонности 1у

Таким образом, в 1-м, 2-м, 3-м и 11-м, 12-м месяцах уро-

вень временного ряда меньше значений тренда, а в 4-м —

10-м этот уровень больше значений тренда.

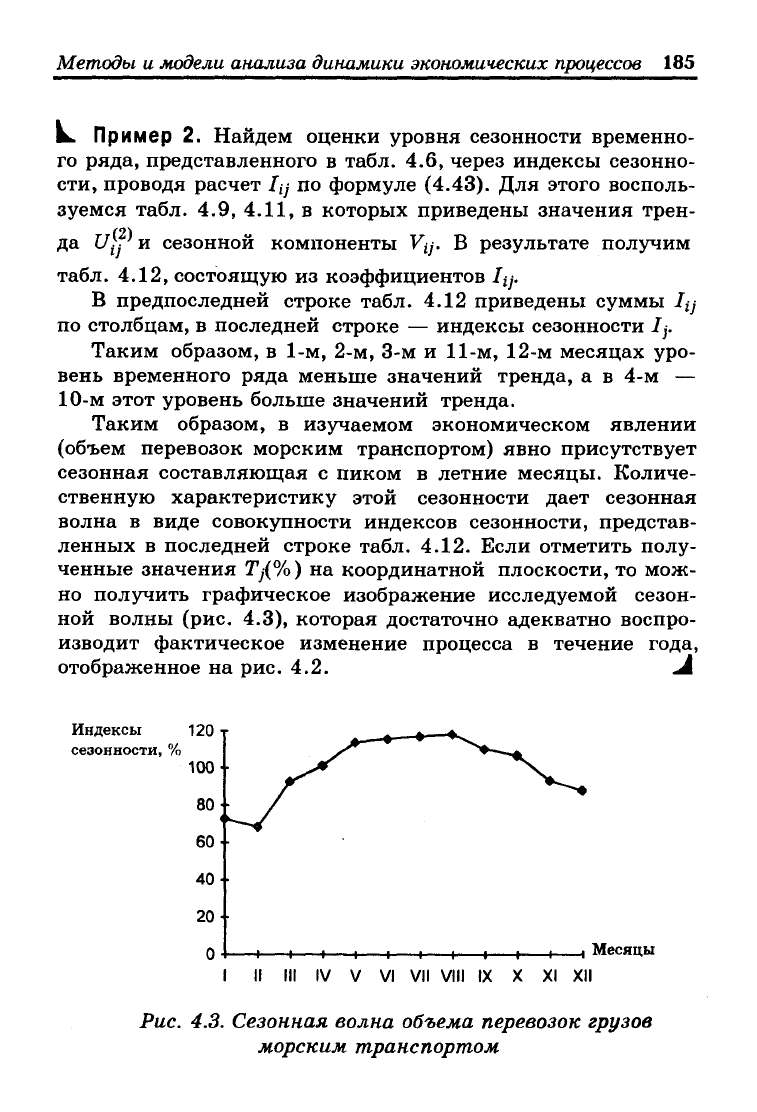
Таким образом, в изучаемом экономическом явлении

(объем перевозок морским транспортом) явно присутствует

сезонная составляющая с пиком в летние месяцы. Количе-

ственную характеристику этой сезонности дает сезонная

волна в виде совокупности индексов сезонности, представ-

ленных в последней строке табл. 4.12. Если отметить полу-

ченные значения Tj(%) на координатной плоскости, то мож-

но получить графическое изображение исследуемой сезон-

ной волны (рис. 4.3), которая достаточно адекватно воспро-

изводит фактическое изменение процесса в течение года,

отображенное на рис. 4.2. Л

Индексы 120

сезонности, %

100

II III IV V VI VII

VIII

IX X XI XII

Рис. 4.3. Сезонная волна объема перевозок грузов

морским транспортом

Месяцы

Год

I'«

/;,%

0,55

0,68

0,73

0,71

0,72

0,74

0,79

0,77

0,80

0,84

8,01

72,80

0,48

0,62

0,63

0,68

0,66

0,67

0,70

0,75

0,73

0,77

0,82

7,51

68,30

1,88

0,91

0,92

0,93

0,94

0,95

0,96

10,18

92,50

1,02

1,01

11,14

101,3

1,23

1,17

1,16

1,14

1,15

1,14

1Д1

1,12

1,10

1,08

12,54

114,0

Месяц

1,26

1,19

1,16

1Д7

1,16

1,15

1,12

1,14

1,12

1,09

12,75

115,9

1,28

1,21

1,20

1,17

1,18

1,16

1,14

1,15

1,13

1,10

12,90

117,3

1,29

1,23

1,22

1,18

1,20

1,19

1,18

1,05

1,16

1,13

1,11

13,04

118,5

1Д7

1,13

1,12

1,10

1,12

1,10

1,08

1,09

1,08

1,06

12,15

110,5

1Д1

1,09

1,08

1,07

1,08

1,07

1,06

1,05

1,04

11,77

107,0

0,89

0,19

0,92

0,94

0,93

0,94

0,95

0,94

0,95

0,96

10,26

93,3

0,81

0,85

0,89

0,87

0,88

0,89

0,90

0,91

0,94

9,69

88,1

Таблица

4.12.

Методы и модели анализа динамики экономических

процессов

187

Вопросы и задания

Дайте определение временного экономического ряда и

характеристику его структурно образующих элементов.

Что такое аномальный уровень временного ряда? Какие

методы обнаружения и устранения аномальных уровней

вы знаете?

Перечислите основные этапы изученных методов опре-

деления наличия тренда.

Поясните суть методов механического сглаживания вре-

менных рядов. Дайте сравнительную характеристику

этих методов.

Назовите основные показатели экономической динами-

ки,

рассчитываемые на основе временных рядов.

6. В чем сущность явления автокорреляции во временных

рядах? Что такое временной лаг?

Дайте характеристику явления сезонности в экономиче-

ских процессах. Какие методы выявления и фильтра-

ции сезонной компоненты временного ряда вы знаете?

8. Поясните суть статистических методов анализа сезонно-

сти.

Что такое сезонная волна?

Упражнения

В таблице приведены годовые данные о трудоемкости

производства 1 т цемента (нормо-смен).

Текущий номер

года (t)

Трудоемкость 1 т

цемента (у,)

7,9

8,3

7,5

6,9

7,2

6,5

5,8

4,9

5,1

4,4

Определить наличие тренда во временном ряду:

а) методом проверки разности средних уровней;

б) методом Фостера—Стьюарта (табличные значения

статистик Стьюдента и Фишера принять равными t

—

2,23;

188

Глава 4

= 3,07; другие необходимые табличные данные приведе-

ны в табл. 4.5).

Сгладить временной ряд, приведенный в упр. 1, мето-

дом простой скользящей средней. Результаты показать на

графике.

Сгладить временной ряд, приведенный в упр. 1, мето-

дом экспоненциального сглаживания, приняв параметр а

экспоненциального сглаживания равным: а) 0,1; б) 0,3. От-

разить результаты сглаживания на графике. Визуально оп-

ределить, какое из этих значений а наиболее соответствует

экономическому процессу, заданному временным рядом.

Для показателя, заданного временным рядом в упр. 1,

определить:

а) средний абсолютный прирост;

б) средние темпы роста и прироста;

в) средний уровень ряда;

г) среднеквадратическое отклонение и дисперсию.

Для временного ряда в упр. 1 рассчитать несколько

первых коэффициентов автокорреляции по формуле (4.18') и

построить график автокорреляционной функции. Найти ве-

личину временного лага.

Глава 5

МОДЕЛИ ПРОГНОЗИРОВАНИЯ

ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ

• Трендовые модели на основе кривых роста

• Оценка адекватности и точности трендовых моделей

• Прогнозирование экономической динамики на основе трендовых

моделей

• Адаптивные модели прогнозирования

5.1.

Трендовые модели на основе кривых роста

Основная цель создания трендовых моделей экономиче-

ской динамики — на их основе сделать прогноз о развитии

изучаемого процесса на предстоящий промежуток времени.

Прогнозирование на основе временого ряда экономических

показателей относится к одномерным методам прогнозиро-

вания, базирующимся на экстраполяции, т.е. на продлении

на будущее тенденции, наблюдавшейся в прошлом. При та-

ком подходе предполагается, что прогнозируемый показа-

тель формируется под воздействием большого количества

факторов, выделить которые либо невозможно, либо по кото-

рым отсутствует информация. В этом случае ход изменения

данного показателя связывают не с факторами, а с течением

времени, что проявляется в образовании одномерных вре-

менных рядов. Рассмотрим метод экстраполяции на основе

так называемых кривых роста экономической динамики.

Использование метода экстраполяции на основе кривых

роста для прогнозирования базируется на двух предположе-

ниях:

• временной ряд экономического показателя действитель-

но имеет тренд, т.е. преобладающую тенденцию;

• общие условия, определявшие развитие показателя в

прошлом, останутся без существенных изменений в тече-

ние периода упреждения.

190 Глава 5

В настоящее время насчитывается большое количество

типов кривых роста для экономических процессов. Чтобы

правильно подобрать наилучшую кривую роста для модели-

рования и прогнозирования экономического явления, необ-

ходимо знать особенности каждого вида кривых. Наиболее

часто в экономике используются полиномиальные, экспо-

ненциальные и S-образные кривые роста. Простейшие поли-

номиальные кривые роста имеют вид:

= а

+ a±t (полином первой степени)

= а

a-^t

t (полином второй степени)

= а

+ o,\t + a

t (полином третьей степени)

и т.д.

Параметр а\ называют линейным приростом, параметр

0-2

— ускорением роста, параметр аз — изменением ускоре-

ния роста.

Для полинома первой степени характерен постоянный

закон роста. Если рассчитать первые приросты по формуле

= y

_i,

t = 2, 3, ..., п,

то

они будут постоянной вели-

чиной и равны Oj.

Если первые приросты рассчитать для полинома второй

степени, то они будут иметь линейную зависимость от вре-

мени и ряд из первых приростов и

, щ,... на графике будет

представлен прямой линией. Вторые приросты u\'~u

- u

_±

для полинома второй степени будут постоянны.

Для полинома третьей степени первые приросты будут

полиномами второй степени, вторые приросты будут линейной

функцией времени, а третьи приросты, рассчитываемые по

формуле uf^ = uf'

-uj_\,

будут постоянной величиной.

На основе сказанного можно отметить следующие свойст-

ва полиномиальных кривых роста:

• от полинома высокого порядка можно путем расчета по-

следовательных разностей (приростов) перейти к поли-

ному более низкого порядка;

• значения приростов для полиномов любого порядка не

зависят от значений самой функции y