Faulon J.L., Bender A. Handbook of Chemoinformatics Algorithms

Подождите немного. Документ загружается.

408 Handbook of Chemoinformatics Algorithms

steps and the fate of carbon atoms within each step must be known a priori. The

system’s input and output fluxes are determined by quantitative physiological param-

eters obtained from the experiment, including nutrient feed, cell growth rates and

densities in the chemostat, and the efflux. The stoichiometric constraints on all inter-

nal fluxes are formulated using the principle of mass conservation, that is, N ·v = 0.

The isotopomer balance equations for the internal reactions are then derived using

either the BNGL/BioNetGen-based method or the IMM-based method. The under-

lying mathematical model for

C MFA is a set of isotopomer balance equations

as shown below in Equations 15.19 through 15.34. Given an initial guess for the

intermediate fluxes, the balance equations, in algebraic or ordinary differential equa-

tion (ODE) form, are used to compute the steady-state or dynamic labeling patterns.

The mathematical model for the dynamic

C labeling experiments is generally a

high-dimensional coupled system of differential algebraic equations, which in fact

constitutes an inverse problem for the unknown intracellular fluxes. Thus, predictions

for the internal fluxes are obtained by minimizing the difference between simulated

and measured isotope patterns. Essentially, this is a complex parameter fitting prob-

lem, which can be solved using a variety of techniques. For steady-state

C labeling

experiments, the model is a set of algebraic equations, and the algorithms employed

for numerical flux estimation are primarily gradient-based local optimization [27] or

gradient-free global optimization [10, 28–30] techniques, such as simulated anneal-

ing or genetic algorithms. In addition, a hybrid technique of global-local optimization

has been applied [31]. For dynamic

C labeling analysis, the system is described by

a set of algebraic–differential equations. Although analysis of dynamic

C label-

ing data has been proposed by a number of groups and used to estimate fluxes in

small metabolic subnetworks [32–34], to the best of our knowledge, this type of

analysis is yet to be used to estimate fluxes in large-scale networks. A barrier to

estimating large numbers of fluxes from this type of data is the large number of

isotopomer balance equations that must be specified. This problem is solved by the

BNGL/BioNetGen-based approach we review here.

Minimizing the objective function [31], that is, the difference between the sim-

ulated and measured labeling patterns using, for example, simulated annealing,

provides new estimates for the internal fluxes. The objective function is given by

Obj =



i=1



(t) −E

(



V, v, t)



, (15.13)

where M

are the N individual labeling measurements and E

their corresponding

simulated values. The quantity δ

is the confidence value of the ith measurement.

For dynamic isotopomer experiments, M

is a function of time, and E

is a function

of time, V represents metabolite pool sizes, and v represents flux distributions. For

steady-state isotopomer experiments, E

is a function of flux distributions (v) only.

Using these revised fluxes, new isotope labeling patterns are generated and again

compared with the observed labeling patterns. This process continues until some

measure of convergence is achieved, for example, the intracellular fluxes do not

Using Systems Biology Techniques to Determine Metabolic Fluxes 409

significantly change between iterations or some predefined number of iterations is

performed.

15.3.2 IMM-BASED APPROACH

We now apply the IMM method to the four-flux problem posed in Figure 15.3 to

determine the metabolic fluxes. For a metabolite S with two carbons, the IDV is

given by



⎛

⎜

⎝

(00)

(01)

(10)

(11)

⎞

⎟

⎠

, (15.14)

where the binary representation (·) corresponds to the state (C1 C2), and 0 and 1

indicate

C and

C, respectively. 0 ≤ I

(j) ≤ 1 is the fraction of S molecules that

show a labeling pattern corresponding to the binary representation of j. We can derive

the IMM for each of the internal reactions directly from the carbon atom fate map

provided in Figure 15.3. IMM

S>M1

denotes the IMM for the reaction between S and

M1. We obtain

IMM

S>M1

⎛

⎜

⎝

1000

0100

0010

0001

⎞

⎟

⎠

, (15.15)

IMM

S>M2

⎛

⎜

⎝

1000

0010

0100

0001

⎞

⎟

⎠

, (15.16)

IMM

M1>P

⎛

⎜

⎝

1000

0100

0010

0001

⎞

⎟

⎠

, (15.17)

IMM

M2>P

⎛

⎜

⎝

1000

0100

0010

0001

⎞

⎟

⎠

. (15.18)

Each column of the IMM indicates how the substrate isotopomer evolves to the

corresponding isotopomers in the product, which is represented by each row. For

example, in IMM

S>M1

, the first column indicates that the isotopomer S

can only

be transferred to a product M1

410 Handbook of Chemoinformatics Algorithms

Again, for a reaction A→B, the isotopomer balance equations can be derived from

Equation 15.1. The corresponding isotopomer balance equations for our four-flux

example are therefore

= v

−(v

, (15.19)

= v

−(v

, (15.20)

= v

−(v

, (15.21)

= v

−(v

, (15.22)

dM1

= v

−(v

)M1

, (15.23)

dM1

= v

−(v

)M1

, (15.24)

dM1

= v

−(v

)M1

, (15.25)

dM1

= v

−(v

)M1

(15.26)

dM2

= v

−(v

)M2

, (15.27)

dM2

= v

−(v

)M2

, (15.28)

dM2

= v

−(v

)M2

, (15.29)

dM2

= v

−(v

)M2

, (15.30)

= v

−v

, (15.31)

= v

−v

, (15.32)

= v

−v

(15.33)

= v

−v

, (15.34)

and are subject to the following algebraic constraints:

= 1, (15.35)

+M1

= 1, (15.36)

Using Systems Biology Techniques to Determine Metabolic Fluxes 411

+M2

= 1, (15.37)

= 1. (15.38)

These equations arise due to the definition of the isotopomer fractions, that is, mass

conservation dictates that these fractions must sum to one. The isotopomer balance

equations coupled with the algebraic constraints comprise a system of differential–

algebraic equations that needs to be solved to determine the dynamic isotopomer

labeling patterns.

15.3.3 BNGL/BIONETGEN-BASED APPROACH

As discussed previously, BioNetGen derives the isotopomer balance equations rel-

evant for a given experiment directly from fate maps and generates the dynamic

distribution of observable metabolites given the input parameters. Here we simulate

the forward problem shown in Figure 15.3 using BioNetGen and generate the iso-

tope labeling patterns given the assumed flux patterns. The BioNetGen input file

for the four-flux example is provided below. It includes several blocks: parameters,

species, reaction rules, and observables. In the first block, the metabolite pool sizes

and the flux estimates, which are the input parameters, are specified. The second

block identifies the species, which are the metabolites, and their initial concentra-

tions. For each differently labeled initial metabolite, define a precursor species with

fixed concentration (defined by prepending the “$” character) corresponding to the

fraction in that labeling state. The block entitled “reaction rules” defines the carbon

atom fate maps. Finally, the observables, or model outputs, are given in the fourth

block. In this input file, the observables are the metabolite isotopomer fractions for

P. For example, the observable pattern P(C1∼1, C2∼0) represents the isotopomer

. The remaining sections are commands for generating the isotopomer balance

equations and simulating the dynamic labeling patterns. Specifically, the next block

of this input file contains commands that generate the detailed isotopomer reac-

tions from the specified reaction rules and write BioNetGen and MATLAB

output

files. The next several sections simulate the dynamic labeling patterns given differ-

ent pool sizes and/or fluxes. The command setParameter() defines the pool sizes

or the fluxes. The system is perturbed by feeding the system with a labeled sub-

strate. In this case, we have labeled 10% at the first carbon position. The command

simulate_ode() runs a simulation of the dynamic trajectories of the isotope labeling

patterns.

begin parameters

# Pools

V_S 1.0

V_M1 1.0

V_M2 1.0

V_P 1.0

412 Handbook of Chemoinformatics Algorithms

# Fluxes

v_v1 0.5

v_v2 0.5

v_v3 0.4

v_v4 0.4

v_vm1 0.1

v_vm2 0.1

v_vp 0.8

v_vs 1.0

# Labeled fraction

f_label 0.1

end parameters

begin species

$proS(C1 ∼0,C2 ∼0) 1-f_label

$proS(C1 ∼1,C2 ∼0) f_label

S(C1 ∼0,C2 ∼0) V_S

M1(C1 ∼0,C2 ∼0) V_M1

M2(C1 ∼0,C2 ∼0) V_M2

P(C1 ∼0,C2 ∼0) V_P

NULL 0

end parameters

begin reaction rules

pros(C1%1,C2%2) -> M1(C1%1,C2%2) v_v1/V_S

S(C1%1,C2%2) -> M1(C1%1,C2%2) v_v1/V_S

S(C1%1,C2%2) -> M2(C1%2,C2%1) v_v2/V_S

M1(C1%1,C2%2) -> P(C1%1,C2%2) v_v3/V_M1

M2(C1%1,C2%2) -> P(C1%1,C2%2) v_v4/V_M2

M1() -> NULL v_vm1/V_M1

M2() -> NULL v_vm2/V_M2

P() -> NULL v_vp/V_P

end reaction rules

begin observables

Molecules P00 P(C1 ∼0,C2 ∼0)/V_P

Molecules P01 P(C1 ∼0,C2 ∼1)/V_P

Molecules P10 P(C1 ∼1,C2 ∼0)/V_P

Molecules P11 P(C1 ∼1,C2 ∼1)/V_P

end observables

Using Systems Biology Techniques to Determine Metabolic Fluxes 413

generate_network({overwrite=>1});

writeSBML();

writeMfile();

saveConcentrations();

imulate_ode({t_end=>20, n_steps=>40});

resetConcentrations();

setParameter(V_yM2, 0.5);

simulate_yode({suffix=>"M2low", t_end=>20,

n_steps=>40});

resetConcentrations();

setParameter(V_yM2, 2.0);

simulate_ode({suffix=>"M2high", t_end=>20,

n{_}ysteps=>40});

resetConcentrations();

setParameter(V_M2, 1.0);

setParameter(v_v1, 0.6);

setParameter(v_v2, 0.4);

setParameter(v_v3, 0.5);

setParameter(v_v4, 0.3);

simulate_ode({suffix=>"dottedline", t_end=>20,

n_steps=>40});

The raw experimental measurements of isotopomer distributions contain the con-

tributions due to naturally occurring isotopes of its elements, such as hydrogen,

carbon, nitrogen, oxygen, and so on. Correction of the isotopomer distribution is

required to take into account differences in the relative natural abundance distribution

of each mass isotopomer (skewing) as described in Ref. [35]. A software tool for this

correction is reported in Ref. [36].

Solving the system of differential algebraic equations presented earlier gives us a

dynamic trajectory of labeling patterns. Figure 15.4 depicts the temporal dynamics

of the reaction product P

from a simulation of the four-flux network. P

indicates

that the second carbon is

C labeled. At time zero, the input feed changes from S

1.0, S

= S

= 0toS

= 0.9, S

= 0, S

= 0.1, and S

= 0, indicating

that 10% of the feed is

C labeled at carbon position 1. We assume the following

values for the fluxes: v

= 1.0, v

= v

= 0.5, v

= v

= 0.4, v

= v

= 0.1,

and v

= 0.8. In Figure 15.4, we study the effect of metabolite pool size on product

dynamics. The pool sizes of the metabolites S, M1, and P are set to 1, and the pool size

of M2 is varied. We see that the pool size has no effect on the steady-state distribution.

Interestingly, however, Figure 15.4 shows that the dynamic labeling patterns depend,

not only on the fluxes, but also on the metabolite pool sizes. Consequently, valuable

information about the relative metabolite pool sizes can potentially be inferred from

plots of the temporal dynamics.

414 Handbook of Chemoinformatics Algorithms

0.05

0.04

0.03

0.02

0.01

0510

Time

15 20

FIGURE 15.4 Dynamic simulation of the four-flux problem. At time zero, the input feed

changes from S

= 1.0, S

= S

= 0toS

= 0.9, S

= 0, S

= 0.1, and S

= 0.

Time evolution of the reaction product with

C at carbon position 2 (P

) for different pool

sizes is plotted. Flux patterns are assumed as follows: v

= 1.0, v

= v

= 0.5, v

= v

= 0.4,

= v

= 0.1, and v

= 0.8. The pool sizes of metabolites S, M1, and P are set to 1, and the

pool size of M2 is varied. M2 = 1 (solid line), M2 = 2 (dashed line), and M2 = 0.5 (dash-dot

line). For the dotted line, flux patterns are assumed as follows: v

= 1.0, v

= 0.6, v

= 0.4,

= 0.5, v

= 0.3, v

= 0.1, v

= 0.1, and v

= 0.8, and the pool sizes of metabolites

S, M1, M2 and P are set to 1. This plot reveals that the dynamics depend on the pool size in

addition to the flux distribution and provide valuable information on the relative pool sizes that

can be used for dynamic labeling experiments. The pool size does not affect the steady-state

distribution.

15.4 DETAILED EXAMPLE OF THE BNGL/BioNetGen-BASED

APPROACH FOR THE CALVIN CYCLE

The Calvin cycle is a series of biochemical reactions required for carbon fixa-

tion. The carbon source for this cycle is CO

. Five metabolites D-ribulose-1,5-

bisphosphate (R5P),

D-erythrose 4-phosphate (E4P), 3-phospho-D-glycerate (G3P),

(2R)-2-hydroxy-3-(phosphonooxy)-propanal (T3P), and

D-fructose 6-phosphate

(F6P) link this pathway with central metabolic pathways. Figure 15.5 provides a net-

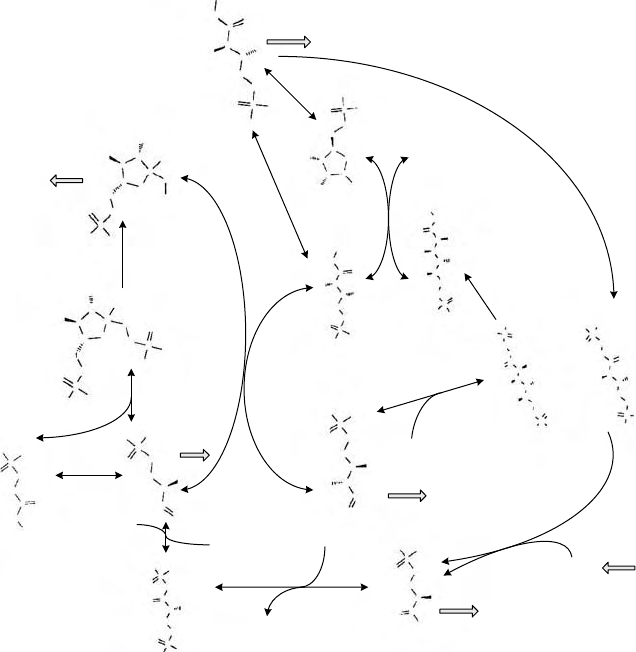
work rendition of the Calvin cycle. The program we developed to visualize chemical

structures, such as that shown in Figure 15.5, uses routines available in the Chemistry

Development Kit [37]. The catalysts involved in the Calvin cycle are functionally

equivalent to those used in other pathways, including the pentose phosphate path-

way and in gluconeogenesis, and therefore, this example may be of interest to a

broad community. The Calvin cycle is of particular interest because this network

involves only a single-carbon input metabolite, and therefore steady-state labeling

Using Systems Biology Techniques to Determine Metabolic Fluxes 415

F6 P

F16P

DHAP

T3P

R5P

R5DP

E4P

G3 P

NAD

NADPH

ADP

ATP

R01512

X5P

DHAP

T3P

R01523

R00024

R01063

R01015

R01068

R00762

R01067

R01829

R01845

R01641

R01529

R01056

Ri5P

S7P

S17P

P13G

FIGURE 15.5 The Calvin cycle. The following abbreviations are used for metabolites in

the network: R5P for

D-ribulose 1,5-bisphosphate, G3P for 3-phospho-D-glycerate, P13G for

3-phospho-

D-glyceroyl phosphate, and T3P for (2R)-2-hydroxy-3-(phosphonooxy)-propanal,

DHAP for glycerone phosphate, F16P for

D-fructose 1,6-bisphosphate, F6P for D-fructose

6-phosphate, E4P for

D-erythrose 4-phosphate, X5P for D-xylulose 5-phosphate, S17P for

D-sedoheptulose 1,7-bisphosphate, S7P for D-sedoheptulose 7-phosphate, Ri5P for D-ribose

5-phosphate, and R5P for

D-ribulose 5-phosphate. The KEGG ID is used for reaction identifi-

cation. There is an input flux feeding the pool of CO

and five flux sinks from pools of R5P,

E4P, G3P, T3P, and F6P. For each metabolite, the carbon index shown in the figure is based

on InChI™ naming. The indices are used to define the carbon atom fate maps as shown in the

BioNetGen input file.

of CO

is completely uninformative. Analysis of the transient labeling patterns of

metabolites is required to learn anything about the internal fluxes from a

C-labeling

experiment.We employ the BNGL/BioNetGen-based approach to determine the intra-

cellular fluxes for the Calvin cycle. The BioNetGen input file shown below specifies

a model and simulation for labeling dynamics in the Calvin cycle (Figure 15.5) when

416 Handbook of Chemoinformatics Algorithms

a feed of unlabeled CO

is replaced with a mixture of unlabeled and

C-labeled

. The raw carbon fate maps need to be processed before they can be used as

BioNetGen input. This preprocessing is described in Ref. [19]. The model tracks 562

isotopomers. In the simulation, the system is taken to be in a steady state. At time

t = 0, the composition of the CO

feed is changed, such that 10% of incoming CO

is labeled with

C. The steady-state fluxes in the system remain unchanged (up to

isotope effects, which are expected to be small), but the

C labeling pattern of each

intermediate metabolite changes until eventually all intermediates are fully labeled.

BioNetGen is capable of simulating the labeling dynamics. BioNetGen can also gen-

erate a specification of the same model and simulation in M-file and Systems Biology

Markup Language (SBML) formats, which can then be interpreted by other software

tools capable of simulating ODEs, such as MATLAB

. For reversible reactions, we

need to specify two fluxes: a forward flux and a backward flux. Instead of using

forward and backward fluxes, reversible reactions can also be modeled using a net

flux and an exchange flux [27]. That is,

net

= v

forward

−v

backward

and v

exchange

= min(v

forward

, v

backward

). (15.39)

The exchange flux can be in the range [0, ∞]. The characterization of forward and

backward fluxes as net and exchange fluxes provides a measure of the reversibility

of a reaction, where an exchange flux of 0 corresponds to irreversible reactions and

infinity (∞) indicates fast reaction equilibrium. Isotopomer distributions are not very

sensitive to exchange fluxes. Because it has been shown that the exchange flux can

only be determined to within an order of magnitude [9], an exchange flux can be

transformed into the so-called [0, 1]-exchange flux,

exchange

∈[0, 1]=

exchange

(1 −v

exchange

)

. (15.40)

In addition, when the exchange flux is very large, numerical instabilities may arise.

In these cases, this range can be specified as, for example, [0.1, 0.9] to remove the

possibility that an exchange flux is either too small or too large. As a measure of the

efficiency of BioNetGen for a problem with some computational complexity (562

isotopomers), we have calculated the CPU time requirements for the Calvin cycle

simulation. On an Intel

Pentium

4 CPU 3.2 GHz machine, the entire simulation

took a total of 33.8 s. It took 14.4 s to generate the isotopomer balance equations from

the BNGL-encoded input and 17.2 s to equilibrate the system, which corresponds to

the first simulate_ode command. The second simulate_ode command runs another

ODE simulation to identify the isotopomer fractions and took 2.2 s. The computational

cost of simulating a set of stiff differential equations typically scales as N

, where

N is the number of equations (number of species). In general, N and the number of

isotopomer balance equations will tend to increase exponentially with the number of

reactions in the metabolic network. However, for a recently reported kinetic Monte

Carlo method [38], the cost of simulation is independent of the number of isotopomers

and scales with the number of reactions (rules).

Using Systems Biology Techniques to Determine Metabolic Fluxes 417

begin parameters

#Pools

V_R5P 1.0

V_R5DP 1.0

V_CO2 1.0

V_G3P 1.0

V_P13G 1.0

V_T3P 1.0

V_DHAP 1.0

V_F16P 1.0

V_F6P 1.0

V_E4P 1.0

V_X5P 1.0

V_Ri5P 1.0

V_S17P 1.0

V_S7P 1.0

# Fluxes

v_R00024 1.00

v_R01512 1.95

v_R01063_f 0.05

v_R01063_b 2.00

v_R01015_f 0.86

v_R01015_b 0.10

v_R01068_f 0.15

v_R01068_b 0.58

v_R00762 0.43

v_R01067_f 0.50

v_R01067_b 0.12

v_R01829_f 0.20

v_R01829_b 0.53

v_R01845 0.33

v_R01641_f 0.43

v_R01641_b 0.10

v_R01529_f 0.10

v_R01529_b 0.82

v_R01056_f 0.50

v_R01056_b 0.17

v_R01523 1.00

vs_T3P 0.05

vs_F6P 0.05

vs_R5P 0.05

vs_E4P 0.05

vs_G3P 0.05

v_vi_CO2_unlabeled 1

v_vi_CO2_labeled 0

end parameters

begin species

R5P(C1 ∼0,C2 ∼0,C3 ∼0,C4 ∼0,C5 ∼0) V_R5P

R5DP(C1 ∼0,C2 ∼0,C3 ∼0,C4 ∼0,C5 ∼0) V_R5DP

CO2(C1 ∼0) V_CO2

G3P(C1 ∼0,C2 ∼0,C3 ∼0) V_G3P

P13G(C1 ∼0,C2 ∼0,C3 ∼0) V_P13G

T3P(C1 ∼0,C2 ∼0,C3 ∼0) V_T3P

DHAP(C1 ∼0,C2 ∼0,C3 ∼0) V_DHAP

F16P(C1 ∼0,C2 ∼0,C3 ∼0,C4 ∼0,C5 ∼0,C6 ∼0) V_F16P

F6P(C1 ∼0,C2 ∼0,C3 ∼0,C4 ∼0,C5 ∼0,C6 ∼0) V_F6P

E4P(C1 ∼0,C2 ∼0,C3 ∼0,C4 ∼0) V_E4P

X5P(C1 ∼0,C2 ∼0,C3 ∼0,C4 ∼0,C5 ∼0)

V_X5P