Faulon J.L., Bender A. Handbook of Chemoinformatics Algorithms
Подождите немного. Документ загружается.

Sequence Alignment Algorithms 377
u
1
u
2
u
3
u
4
u
5
u
6
u
7
G06886
G05554
u
2
u
1
u
3
u
4
u
5
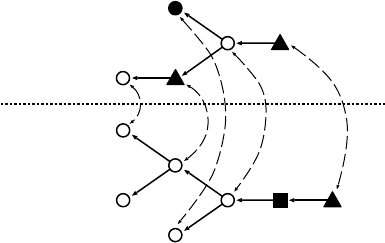
FIGURE 13.7 An example of global glycan alignment.
Recall that nodes are numbered according to the postorder traversal. For the
simplicity of presentation, we use the following score function and gap penalty:
w(u, v) =
1, if label(u) = label(v),
0, otherwise,
d(v) = d(u) =−1 for all nodes u ∈ V(T
1
) and v ∈ V(T
2
).
The algorithm initializes F[i,0] and F[0, j] as follows:
F[1, 0]=−1, F[2, 0]=−1, F[3, 0]=−2, F[4, 0]=−4, F[5, 0]=−5
F[0, 1]=−1, F[0, 2]=−1, F[0, 3]=−3, F[0, 4]=−1,
F[0, 5]=−5, F[0, 6]=−6, F[0, 7]=−7
Next, it determines the values of F[1, j] as follows:
F[1, 1]=0, F[1, 2]=0, F[1, 3]=−2, F[1, 4]=0, F[1,
5]=−4,
F[
1, 6]=−5, F[1, 7]=−6
It is to be noted that the value of F[1, 3] is determined by F[1, 3]=w(u
1
, v
3
) +
F[0, 1]+F[0, 2]. Similarly, the algorithm determines the values of F[2, j]as follows:
F[2, 1]=1, F[2, 2]=1, F[2, 3]=−1, F[2, 4]=1, F[2, 5]=−3,
F[2, 6]=−4, F[2, 7]=−5
Then, it determines the values of F[3, j] as follows:
F[3, 1]=0, F[3, 2]=0, F[3, 3]=0, F[3, 4]=0, F[3, 5]=−2,
F[3, 6]=−3, F[3, 7]=−3
378 Handbook of Chemoinformatics Algorithms
It is to be noted that the value of F[3, 3] is determined by F[3, 3]=w(u
3
, v
3
) +
F[2, 1]+F[0, 2](or F[3, 3]=w(u
3
, v
3
) +F[0, 1]+F[2, 2]). Then, it determines the
values of F[4, j] and F[5, j] as follows:
F[4, 1]=−2, F[4, 2]=−2, F[4, 3]=1, F[4, 4]=−2,
F[4, 5]=1, F[4, 6]=0, F[4, 7]=−1
F[5, 1]=−3, F[5, 2]=−3, F[5, 3]=0, F[5, 4]=−3,
F[5, 5]=0, F[5, 6]=1, F[5, 7]=1
Finally, the score of the global glycan alignment is given as F[5, 7]=1 and the
alignment is obtained as
A ={(u
1
, v
4
), (u
2
, v
1
), (u
3
, v
3
), (u
4
, v
5
), (u
5
, v
7
)},
where this alignment comes from the following:
F[5, 7]=w(u
5
, v
7
) +F[4, 6],
F[4, 6]=d(v
6
) +F[4, 5],
F[4, 5]=w(u
4
, v
5
) +F[1, 4]+F[3, 3],
F[1, 4]=w(u
1
, v
4
),
F[3, 3]=w(u
3
, v
3
) +F[2, 1]+F[0, 2],
F[2, 1]=w(u
2
, v
1
).
In the case of local glycan alignment, F[i,0] and F[0, j] are initialized to be 0, and
the other F[i, j] are determined as follows:
F[1, 1]=0, F[1, 2]=0, F[1, 3]=0, F[1, 4]=0, F[1, 5]=0, F[1, 6]=0, F[1, 7]=0,
F[2, 1]=1, F[2, 2]=1, F[2, 3]=1, F[2, 4]=1, F[2, 5]=1, F[2, 6]=0, F[2, 7]=0,
F[3, 1]=0, F[3, 2]=0, F[3,
3]=1, F[
3, 4]=0, F[3, 5]=1, F[3, 6]=1, F[3, 7]=1,
F[4, 1]=1, F[4, 2]=1, F[4, 3]=1, F[4, 4]=1, F[4, 5]=2, F[4, 6]=1, F[4, 7]=1,
F[5, 1]=0, F[5, 2]=0, F[5, 3]=1, F[5, 4]=0, F[5, 5]=1, F[5, 6]=2, F[5, 7]=2.
In this case, optimal alignments can be obtained by the traceback procedure begin-
ning from any of F[4, 5], F[5, 6], F[
5, 7]. Beginning from F[4, 5], one of the local
alignments will be
A ={(u
1
, v
4
), (u
2
, v
1
), (u
3
, v
3
), (u
4
, v
5
)},
which corresponds to a global alignment between T
1
({u
1
, u
2
, u
3
, u
4
}) and
T
2
({v
1
, v
3
, v
4
, v
5
}). Beginning from F[5, 7], one of the local alignments will be
A ={(u
2
, v
3
), (u
3
, v
5
), (u
4
, v
6
), (u
5
, v
7
)}
Sequence Alignment Algorithms 379
which corresponds to a global alignment between T
1
({u
2
, u
3
, u
4
, u
5
}) and
T
2
({v
3
, v
5
, v
6
, v
7
}).
13.8 KCaM WEB SERVER
The above mentioned algorithms were implemented in the KCaM web server [2].
KCaM is a kind of search tool for the KEGG Glycan database [1]. Though the codes
are not available in public, users can use the algorithms through the web server. As in
the Blast tool for sequence homology search, KCaM requires each user to specify a
query glycan structure and then searches glycan structures similar to the given query
structure in the KEGG Glycan database or the CarbBank database.
There exist three ways for inputting a query glycan structure. One way is to specify
the KEGG Glycan ID number. Each glycan data stored in the KEGG Glycan database
has its own ID number like G00001. Thus, users can use this ID number to specify
a query structure. Another way is to create a KCF (KEGG Chemical Function) file
where KCF is a special format for describing chemical structures including glycans.
The other way is to use the glycan structure editor in the KEGG Glycan database. It
is a user-friendly graphical interface for entering any glycan structure via the web.
Users can also input a KCF format file and modify it.
After specifying a query glycan structure, users can choose search algorithms,
where KCaM provide the following search algorithms.
Gapped & Global: Combination of approximate (i.e., gapped) and global glycan
alignment
Gapped & Local: Combination of approximate and local glycan alignment
Ungapped & Global: Combination of exact (i.e., ungapped) and global glycan
alignment
Ungapped & Local: Combination of exact and local glycan alignment
Furthermore, users can change optional parameters such as gap penalty and weight
of matches and can choose the target database (the KEGG Glycan database or the
CarbBank database).
Once the search algorithm has been selected, KCaM is invoked and structures in
the database are listed from the highest score to the lowest score. Of course, users can
specify the number of structures shown per page. Users can also specify whether or
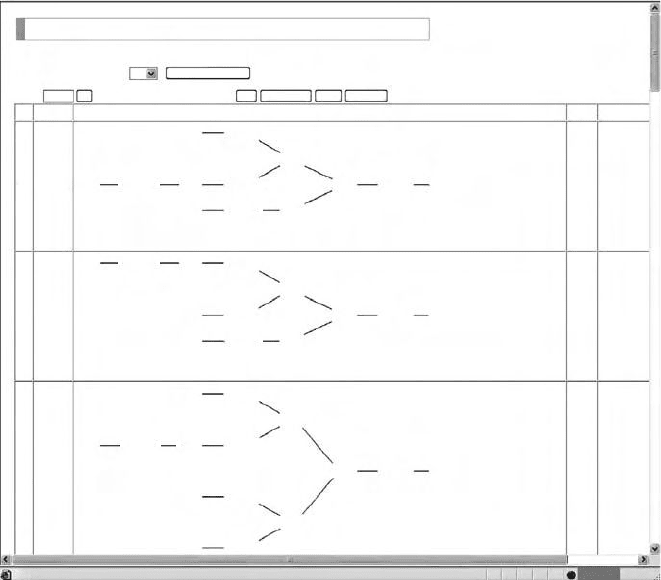
not structures are shown in the list. A snapshot of a KCaM search result is shown in
Figure 13.8.
13.9 CONCLUDING REMARKS
We have explained algorithms for glycan alignment. The algorithms are simple and
fast enough for practical use. The algorithms were implemented in the KCaM web
server, on which search against more than 10,000 glycan structures can be done in
several or several tens of seconds. Furthermore, users can adjust several parameters
(e.g., gap penalty, weight of matches) used in the algorithms via the web.
380 Handbook of Chemoinformatics Algorithms
Glycan data search result
20
Hide structure
To p
No
1
2
3
G03993
Entry
G04020
G04020
G03993
G03684
Structure Name Composition
(Gal)4
(GlcNAc)6
(Man)3
(Gal)4
(GlcNAc)6
(Man)3
(Gal)5
(GlcNAc)7
(Man)3
Page: 1
Go of 72 Items : 1– 20 of 1433
Top Previous Next Bottom
b1
b1
b1 2
b1 b14
a1
a1
6
6
3
2
Gal GlcNAc
b1 4
Gal GlcNAc GlcNAc
GlcNAc
4
GlcNAc
Gal
b1 b1 b1
Gal
Man
Man
b1
b1
b1 b14
a1
a1
6
6
3
2
GlcNAc
4
GlcNAcMan
Man
b1
b1
b1
b1
a1
a1
6
6
3
2
b1 4
GlcNAc
4
GlcNAcMan
Man
4
2
Man
Man
b1
434
Gal GlcNAc GlcNAcGal
b1 b1 b1434
GlcNAc
Similarity-score : 1300
Similarity-score : 1250
4
Gal
b1
GlcNAc
4
Gal
b1 b1
GlcNAc Man
4
Gal
b1
GlcNAc
4
2
Gal
b1
Gal
b1b1
GlcNAc
4
GlcNAc
4
Gal
b1
GlcNAc
4
Gal
b1
GlcNAc
4
2
Number of entries in a page
FIGURE 13.8 Snapshot of KCaM search result.
The most crucial drawback of the current glycan alignment algorithms lies in the
deletion operation. As seen in Figure 13.6, if a node is deleted, only one subtree
branching from the node can survive and the other subtrees are deleted. On the other
hand, under the standard definition of tree edit distance, if a node is deleted, all of
subtrees branching from the node can survive and become descendants of the parent
of the deleted node. If we could use this definition of the deletion operation, more
flexible matching would be possible. However, it is known that the tree edit distance
problem is NP-hard for unordered trees [16], though it is polynomial time solvable
for ordered trees. It suggests that it is almost impossible to develop polynomial time
algorithms for glycan alignment with standard deletion operations if glycan structures
are regarded as unordered trees. However, some practical algorithm was developed
for tree edit distance for unordered trees using the A
∗
algorithm [17]. Based on that
algorithm, more flexible algorithms for glycan alignment might be developed.
REFERENCES
1. Hashimoto, K., Goto, S., Kawano, S., Aoki-Kinoshita, K. F., Ueda, N., Hamajima, M.,
Kawasaki, T., and Kanehisa, M., KEGG as a glycome informatics resource. Glycobiology
2006, 16, 63R–70R.
Sequence Alignment Algorithms 381
2. Aoki, K. F.,Yamaguchi, A., Ueda, N., Akutsu, T., Mamitsuka, H., Goto, S., and Kanehisa,
M., KCaM (KEGG carbohydrate matcher): A software tool for analyzing the structure of
carbohydrate sugar chains. Nucleic Acids Res. 2004, 32, W267–W272.
3. Aoki, K. F., Yamaguchi, A., Okuno, Y., Akutsu, T., Ueda, N., Kanehisa, M., and
Mamitsuka, H., Efficient tree-matching methods for accurate carbohydrate database
queries. Genome Inform. 2003, 14, 134–143.
4. Aoki, K. F., Mamitsuka, H., Akutsu, T., and Kanehisa, M., A score matrix to reveal the
hidden links in glycans. Bioinformatics 2005, 21, 1457–1463.
5. Hashimoto, K., Aoki-Kinoshita, K. F., Ueda, N., Kanehisa, M., and Mamitsuka, H., A new
efficientprobabilistic model for mining labeled ordered treesapplied to glycobiology. ACM
Trans. Knowl. Discov. Data 2008, 2, Article No. 6.
6. Kuboyama, T., Hirata, K., and Aoki-Kinoshita, K. F., Efficient unordered tree kernel and
its application to glycan classification. Lect. Notes Comput. Sci. 2008, 5012, 184–195.
7. Yamanishi, Y., Bach, F., and Vert, J-P., Glycan classification with tree kernels. Bioinfor-
matics 2007, 23, 1211–1216.
8. Kawano, S., Hashimoto, K., Miyama, T., Goto, S., and Kanehisa, M., Prediction of
glycan structures from gene expression data based on glycosyltransferase reactions.
Bioinformatics 2005, 21, 3976–3982.
9. Shan, B., Ma, B., Zhang, K., and Lajoie, G., Complexities and algorithms for glycan
sequencing using tandem mass spectrometry. J. Bioinfor. Comput. Biol. 2008, 6, 77–91.
10. Bille, P., A survey on tree edit distance and related problem. Theoret. Comput. Sci. 2005,
337, 217–239.
11. Zhang, K., RNA structure comparison and alignment. In J. T-L. Wang, et al. (Eds.) Data
Mining in Bioinformatics; Springer: Heidelberg, 2005, pp. 59–81.
12. Tai, K-C., The tree-to-tree correction problem. J. ACM 1979, 26, 422–433.
13. Zhang, K. and Shasha, D., Simple fast algorithms for the editing distance between trees
and related problems. SIAM J. Comput. 1989, 18, 1245–1262.
14. Klein, P. N., Computing the edit-distance between unrooted ordered trees. Lect. Notes
Comput. Sci. 1998, 1461, 91–102.
15. Demaine, E., Mozes, S., Rossman, B., and Weimann, O., An optimal decomposition
algorithm for tree edit distance. Lect. Notes Comput. Sci. 2007, 4596, 146–157.
16. Zhang, K. and Jiang, T., Some MAX SNP-hard results concerning unordered labeled trees.
Inf. Proc. Lett. 1994, 49, 249–254.
17. Horesh,Y., Mehr, R. and Unger, R., Designing anA
∗
algorithm for calculating edit distance
between rooted-unordered trees. J. Comput. Biol. 2006, 13, 1165–1176.
18. Jiang, T., Wang, L., and Zhang, K., Alignment of trees—an alternative to tree edit. Theoret.
Comput. Sci. 1995, 143, 137–148.
19. Edmonds, J. and Matula, D., An algorithm for subtree identification. SIAM Rev. 1968, 10,
273–274.
20. Akutsu, T., An RNC algorithm for finding a largest common subtree of two trees. IEICE
Trans. Inf. Syst. 1992, E75-D, 95–101.
21. Akutsu, T., A Polynomial time algorithm for finding a largest common subgraph of almost
trees of bounded degree. IEICE Trans. Fundam. 1993, E76-A, 1488–1493.
22. Yamaguchi, A., Aoki, K. F., and Mamitsuka, H., Finding the maximum common subgraph
of a partial k-tree and a graph with a polynomially bounded number of spanning trees. Inf.
Proc. Lett. 2004, 92, 57–63.
23. Durbin, R., Eddy. S., Krogh, A., and Mitchison, G., Biological sequence analysis: Prob-
abilistic models of proteins and nucleic acids. Cambridge University Press: Cambridge,
UK, 1998.

14
Machine Learning–
Based Bioinformatics
Algorithms
Application to Chemicals
Shawn Martin
CONTENTS
14.1 Applications of Clustering....................................................383
14.1.1 Applications in Bioinformatics .....................................386
14.1.2 Applications in Chemoinformatics .................................387
14.1.3 Comparisons.........................................................387
14.2 Applications of Classification and Regression ..............................388
14.2.1 Applications in Bioinformatics .....................................390
14.2.2 Applications in Chemoinformatics .................................391
14.2.3 Comparisons.........................................................394
References ............................................................................394
14.1 APPLICATIONS OF CLUSTERING
Clustering refers to an array of data analysis techniques that can be used to partition a
dataset into groups [1,2]. Clustering is generally used as a first pass through a dataset
about which little is known in an effort to organize the information for further analysis.
Once this information is organized in some way, the user will often make additional
hypotheses and/or perform additional analysis.
Clustering techniques are often divided into two categories: hierarchical and parti-
tional. In hierarchical clustering (for background see Ref. [1]), a dataset is organized
into a tree structure known as a dendrogram. The tree is typically drawn upside down
with the trunk at the top of the page and the leaves at the bottom. In this drawing, the
vertical axis is proportional to the similarity of the nodes in the tree so that clusters
can be obtained by drawing a horizontal line through the tree and taking clusters to
be subtrees below that line. An example is shown in Figure 14.1.
There are two main approaches to hierarchical clustering: agglomerative and divi-
sive. In agglomerative clustering, the dendrogram is formed from the bottom (leaves)
up by merging nodes to form clusters. In divisive clustering, the dendrogram is formed
383
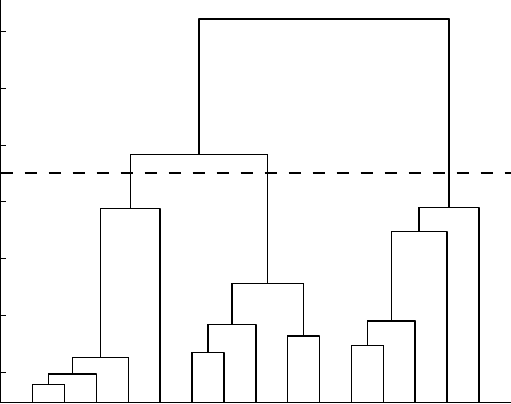
384 Handbook of Chemoinformatics Algorithms
14 15 12 11 13 6 10 7 8 9 1 4 5 2 3
0.2
0.4
0.6
0.8
1
1.2
1.4
FIGURE 14.1 A dendrogram produced by hierarchical clustering, with clusters taken to
be subtrees beneath the horizontal line. This dendrogram was produced using 15 artificially
generated data points consisting of three clusters arranged linearly with approximately one unit
between them. The x-axis shows the data point indices and the y-axis shows the single-link
Euclidean distance between the clusters.
from the top (trunk) down by dividing the dataset into smaller and smaller clusters.
Agglomerative clustering is the more common approach.
Within agglomerative methods, there are several variations available for deciding
when to merge two clusters. The more common methods are single-link, average-
link, and complete-link clustering. Single-link clustering merges two clusters based
on the closest two data points within the two clusters; average-link clustering merges
two clusters based on the centroids of the two clusters; and complete-link clustering
merges clusters based on the maximum distance between two data points within
the two clusters. Agglomerative hierarchical clustering proceeds in the following
manner:
ALGORITHM 14.1 AGGLOMERATIVE HIERARCHICAL CLUSTERING
1. Compute a pair-wise distance matrix for all available samples. Distance here
can be any of a number of possibilities, including Euclidean, Mahalanobis,
and Hamming.
2. Search the distance matrix for the most similar pair of clusters, as measured
using single-link, complete-link, average-link, or other method. Merge the
most similar clusters.
3. Update the distance matrix to reflect distances between clusters.
4. Repeat steps 2 and 3 until there is only one cluster left.
Machine Learning–Based Bioinformatics Algorithms 385
Actual code for hierarchical clustering is widely available. Commercial appli-
cations include MATLAB
(http://www.mathworks.com) and SAS (http://www
.sas.com). There are also open source codes available [3].
In chemoinformatics, the most common method of hierarchical clustering is
agglomerative using Ward’s method for merging clusters [4]. Ward’s method uses
square error, also known as within-cluster-variance, to measure distance between
clusters. Square error is defined as
e
2
=
s
r=1
x
r
−x
c
2
, (14.1)
where x
c
is a cluster centroid and r ranges over the points in the cluster. For the case
of cluster-to-cluster distance, r ranges over the points in a neighboring cluster. Ward’s
method has the advantage of minimizing total cluster variance (it is also known as
the minimum variance method).
Hierarchical clustering is a favorite method in bioinformatics, owing to the fact
that the dataset is not only partitioned, but visualization is also provided. Further,
multiple partitions can be obtained by using a different horizontal threshold to cut
the dendrogram. However, hierarchical clustering suffers from a computational lim-
itation. Hierarchical clustering is memory intensive O(n
2
) and time intensive O(n
2
log n). There are, of course, numerous variations on hierarchical clustering that boast
better performance (see, e.g., Refs. [5,6]).
Partitional clustering algorithms more strictly follow the definition of clustering
previously given, in that partitional methods supply only a partition of a dataset,
with no effort at visualization or different possible partitions. The most common
partitional method is probably k-means. In chemoinformatics, however, a method
known as Jarvis–Patrick clustering [7] is generally preferred. The popularity of the
Jarvis–Patrick method in chemoinformatics has resulted from early publications by
Willett et al. [8–10] comparing different clustering techniques. The method itself
works by comparing data points with neighboring data points to form clusters. The
algorithm proceeds in two steps:
ALGORITHM 14.2 JARVIS–PATRICK CLUSTERING
1. Generate a list of top k neighbors for each data point, using (for example)
Euclidean distance or the Tanimoto coefficient [11]
2. Cluster points according to the following criterion (points that fail a, b, or c
below are not in the same cluster)
a. Data point i is in the top k neighbors of data point j
b. Data point j is in the top k neighbors of data point i
c. Data points i and j have at least k
min
of their top k neighbors in common
The Jarvis–Patrick algorithm is O(n
2
) in time and O(n) in space, making it more
applicable to large datasets than hierarchical clustering. The Jarvis–Patrick method
is readily available from Daylight software (http://www.daylight.com).

386 Handbook of Chemoinformatics Algorithms
A
5
4
3
2
1
0
–1
–2
–3
–4
–5
Vxlnsight cluster
B
C
D
E
F
FIGURE 14.2 A prototypical heat map/dendrogram combination plot produced using
hierarchical clustering of gene expression data. This plot originally appeared in Wil-
son et al. [16] and was produced using the clustering algorithms available in MATLAB
(http://www.mathworks.com).
14.1.1 APPLICATIONS IN BIOINFORMATICS
Most of the clustering applications in bioinformatics havebeen drivenby the availabil-
ity of postgenomic data, and in particular, the advent of microarray gene expression
data. Gene expression data are taken from a high-throughput experimental method
using microarrays [12,13]. A microarray consists of a glass slide with a printed array
of microscopic dots, each containing cDNA. When an experiment is performed, gene
expression is measured via the amount of mRNA that binds to the cDNA on each
spot. Flourophores are used to detect when mRNA binds to a given spot.
Perhaps the earliest application of clustering in bioinformatics was using gene
expression data. In the work of Eisen et al. [14], the yeast cell cycle was analyzed using
microarray data from [15] and hierarchical clustering. Genes were grouped together
according to correlation through time using average link hierarchical clustering. The
results were displayed using a heat map for gene expression combined with a dendro-
gram tree for grouping genes. Eisen’s heat maps are now a standard in bioinformatics.
An example is shown in Figure 14.2 using data taken from Wilson et al. [16].
In addition to hierarchical clustering of gene expression data, numerous other
methods have been applied and/or developed [2,17]. These methods include stan-
dard algorithms such as k-means [18] and self-organizing maps (SOMs) [19], as
well as algorithms developed specifically for microarray data. Microarray-specific
algorithms include graph theoretic algorithms such as cluster identification via
Machine Learning–Based Bioinformatics Algorithms 387
connectivity kernels (CLICK) [20] and the cluster affinity search technique (CAST)
[21]. Other algorithms specialized to microarray data relate to the simultaneous clus-
tering of genes (rows) and samples (columns) in a dataset. These algorithms include
biclustering [22] and coupled two-way clustering (CTWC) [23].
Microarray data are by far the most commonly clustered data in bioinformatics.
However, if we expand our definition of clustering just slightly we encounter two
other data types that have received a lot of attention. The first is protein data. Protein
data are often grouped according to methods such as BLAST to infer function [24].
These types of methods cluster proteins together according to similarity of sequence
(homology) and then make predictions about function and interaction.
There has also been substantial effort exerted toward grouping and organizing
scientific papers published in medicine and biology and tracked by MEDLINE and
PubMed (http://www.pubmed.gov). By analyzing these papers, practitioners hope to
make information more readily available to researchers and (potentially) combine
information across disciplines to achieve greater insight [25,26].
14.1.2 APPLICATIONS IN CHEMOINFORMATICS
Drug discovery is one of the central motivations for the use of clustering in
chemoinformatics [4]. Recently, there has also been interest in materials design
[27]. Hence, most applications are to combinatorial chemistry data, high-
throughput screening (HTS) data [28] and quantitativestructure–activity relationships
(QSARs)/quantitative structure–property relationships (QSPRs) [4,29,30].
In combinatorial chemistry, libraries of chemicals are simultaneously created.
These libraries can then be subjected to HTS. In HTS, (up to) hundreds of thou-
sands of chemicals are arranged on grids so that they may be tested simultaneously
for various properties. These datasets are similar in philosophy to gene expression
arrays; hence, it is natural to apply clustering algorithms HTS data. Unlike gene
expression data, however, the goal of HTS analysis is to select a heterogeneous sub-
set of chemicals that still represent the entire library [4]. This subset is then used for
further study or calculation.
Applications in chemoinformatics tend to favor two clustering algorithms. The
favorite method is the Jarvis–Patrick algorithm. One of the first applications of
the Jarvis–Patrick algorithm to a large chemical dataset (containing ∼240,000
compounds) was performed using two-dimensional fragment descriptors [31]. Jarvis–
Patrick variants are also commonly used to cluster HTS data [32–35] and improve
QSAR analysis by selecting clusters containing representative chemicals [36].
k-means have also been used in combination with QSAR [37].
The next most commonly used method in chemoinformatics is agglomerative hier-
archical clustering using the Ward criterion for merging clusters. Like Jarvis–Patrick
clustering, Ward hierarchical clustering has also been used to provide better sampling
of a compound dataset [38,39] as well as to improve QSAR performance [40].
14.1.3 COMPARISONS
In comparing the usage of clustering in bioinformatics and chemoinformatics, we
can conclude that bioinformatics uses a much wider variety of algorithms, but that
