Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

8.1. Vector-Valued Distributions. Supports, Convergence, Structure Results

467

shows, Theorem 8.1.5 and the equivalent Lemma 8.1.3 do not admit a global

version even in the scalar case.

8.1.6 Remark. Note that if U = 0 for t < a, it results that f = 0 for t < a.

This follows from the fact that rl(t - s) = 0 for s >_ t. Note also that if U has

compact support (that is, if U E P(E)), then the function f can be chosen

in such a way that (7.1.16) holds in 0 (we only have to take 2' containing

the support of U); the result is global in this case.

As an immediate consequence of Theorem 8.1.6, we obtain

8.1.7 Corollary. Let U E 6D'(2; E), and assume

supp(U) = (0).

Then

U=S®uo+S'®u,+ +S(m)®um

(8.1.21)

for some integer m and u0, u1,...,um E E.

Proof. Write

U = f(m)

where f (t) = 0 for t < 0. Since U = 0 in t > 0, it follows from Lemma 8.1.1

that f must coincide there with a polynomial of degree < m - 1. Differenti-

ating, (8.1.21) follows.

We close this section with a " uniform" version of Theorem 8.1.5.

Bounded set of distributions are defined in the same fashion as for test

functions: a set Q.L c 6 '(S2; E) is bounded if and only if, for every sequence

C Q?l, and every sequence (en) of real numbers with e - 0, we have

0 in 6 '(S2; E). (8.1.22)

It is easy to see that Xt is bounded if and only if for every bounded set

`JC c 6 (S2) there exists a constant C such that

IIU(T)II<C (p EX, UE'21,).

(8.1.23)

8.1.8

Theorem. Let 6k be a bounded set in 6 '(S2; E), SZ' a bounded

open subset of S2 with n' c Q. Then the integer m in (8.1.16) can be chosen

independently of U and the functions f are uniformly bounded on compact

subsets of R.

Theorem 8.1.8 is a consequence of the following uniform version of

Lemma 8.1.3.

&1.9 Lemma.

Let X..L be a bounded set in 6D'(2; E), K a compact

subset of Q. Then there exists an integer p > 0 and a constant C independent of

468

The Cauchy Problem in the Sense of Vector-Valued Distributions

U such that

II00II<C1101,

(8.1.24)

for all U E 2L and all p E 6D with support in K.

The proof is much like that of Lemma 8.1.3. If (8.1.24) does not hold

for any p, there exists a sequence {q),,) in 6D, each qq with support in K, and

a sequence

in 6k such that

IIU,,(T,,)II>nII'p II,,

(n>,1).

We consider this time the sequence Jn = %, /I I (Pn I I

Obviously, (i n) is

bounded in 6D(0), but is unbounded, contradicting (8.1.23).

To prove Theorem 8.1.8 we only have to recall that the functions f

are given by (8.1.19) and use (8.1.24).

A generalized sequence (Ua) in 61'(S2; E) is said to be boundedly

convergent to U E 6 '(Sl; E) (in symbols, Ua - U) if and only if Ua - U and

(Ua) is bounded. It is easy to see that bounded convergence and convergence

coincide for sequences, but this is not the case for arbitrary generalized

sequences.

8.1.10

Theorem.

Let (U,) be a generalized sequence of distributions

converging boundedly to zero in 6 '(S2; E), Sl' an open bounded subset of Sl

with D' C: Q. Then there exists a generalized sequence (fa) of continuous

E-valued functions in R, bounded and converging to zero uniformly on compact

subsets of R such that

Ua= f(m)

in Sl'.

This result is an immediate consequence of Theorem 8.1.8: it suffices to note

that the functions fa are defined by (8.1.19) with U = Ua.

8.2. VECTOR-VALUED DISTRIBUTIONS.

CONVOLUTION, TEMPERED DISTRIBUTIONS,

LAPLACE TRANSFORMS

We shall only define convolution in a very particular case. Throughout this

section E, F, G will be three Banach spaces, (u, v) - uv a bounded bilinear

map from E X F into G, U E 6

' (E), V E' +(F). Assume, for the sake of

simplicity, that U and V have support in t >, 0 and let c > 0. Making use of

Theorem 8.1.5 we see that there exist two nonnegative integers m, p, a

continuous E-valued function that vanishes for t < 0 and a continuous

F-valued function g equal to zero in t < 0 such that

U = f(m)

(t < c), (8.2.1)

V=g(p)

(t < c).

(8.2.2)

8.2. Convolution, Tempered Distributions, Laplace Transforms

469

We define

U*V=(f*g)lm+P)

(8.2.3)

in t < c, that is, for every (p E 6D with support in (- oo, c). Here f * g is the

ordinary convolution off and g,

(f*g)(t)_ ff(t-s)g(s)ds, (8.2.4)

where the interval of integration is actually 0 < s < t. (Note that f * g is

continuous.) Since c may be arbitrarily large, it is clear that the definition

above works for any (p E 6D, but it is not immediately apparent that it does

not depend on the choice of the representations (8.2.1) and (8.2.2), which

are obviously not unique. Assume, say, that we replace (8.2.1) by

U=f,(mi)

(t <c1).

We may assume that m < m, and c < c, (the other possibilities are dealt

with in a similar way). Since (f - fl" m))(m) = 0 in t < c, it follows from

Lemma 8.1.1 that f - f i m 1 - m) is a polynomial in t < c. But both f and f, are

zero for t < 0, thus f = flmi-m) and f, is continuously differentiable

at least

m, - m times in t < c. Then we have, after a clearly permissible differentia-

tion under the integral sign,

(fl * g)" =

(fl(m'-m) * g)(m)

= (f * g)(m)

in t < c. This proves that U * V is defined independently of the particular

representations (8.2.1), (8.2.2) chosen. The definition can be easily extended

to the case where U = 0 for t < a, V = 0 for t < b; we omit the details.

It is a rather simple consequence of the construction of U * V that

(U * V)(k) = U(k) * v= U * V(k) (8.2.5)

for any U, V and any integer k >, 0.

It can also be easily seen that if U = 0 in t < a and V = 0 in t < b,

then U * V = 0 in t < a + b. On the other hand, assume that U = 0 fort > a'

and V = 0 for t > b'. Take c so large that the interval t < c contains both the

supports of U and V. Then the function fin (8.2.1) must be a polynomial of

degree < m -1 in t > a' and g must likewise be a polynomial of degree

< p - 1 in t > b'. Hence f * g is a polynomial of degree < m + p -1 in

t > a' + b', which implies that U * V = 0 in t >, a' + b'. We can summarize

these observations in the formula

(supp(U* V))`c (suppU)`+(supp(V))(8.2.6)

where (

)`' indicates convex hull.

It is immediate from its definition that the map (U, V) --> U * V from

6D +(E) x 6 +(F) into 6D +(G) is bilinear. We also have the following con-

tinuity property:

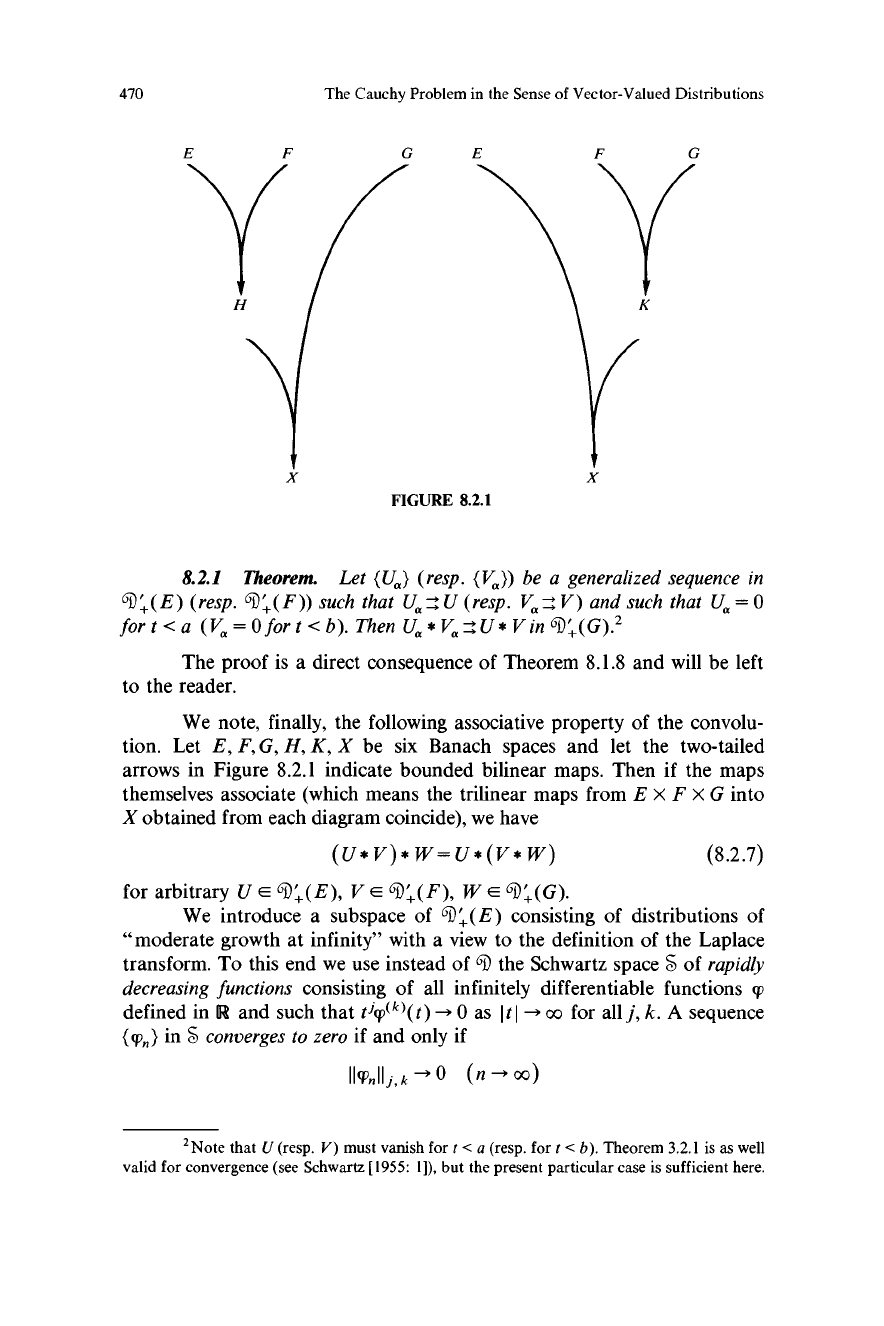
470 The Cauchy Problem in the Sense of Vector-Valued Distributions

FIGURE 8.2.1

8.2.1

Theorem.

Let (Ua) (resp. (V,)) be a generalized sequence in

6D+(E) (resp. 6 +(F )) such that Ua U (resp. Va ; V) and such that Ua = O

fort <a (Va=O fort<b).Then Ua*Va-_ U*Vin 6D' (G).Z

The proof is a direct consequence of Theorem 8.1.8 and will be left

to the reader.

We note, finally, the following associative property of the convolu-

tion. Let E, F, G, H, K, X be six Banach spaces and let the two-tailed

arrows in Figure 8.2.1 indicate bounded bilinear maps. Then if the maps

themselves associate (which means the trilinear maps from E X F X G into

X obtained from each diagram coincide), we have

(U*V)*W=U*(V*W) (8.2.7)

for arbitrary U E 6D'(E), V E 61. +(F), W E 61. +(G).

We introduce a subspace of 6 +(E) consisting of distributions of

"moderate growth at infinity" with a view to the definition of the Laplace

transform. To this end we use instead of 6D the Schwartz space S of rapidly

decreasing functions consisting of all infinitely differentiable functions (V

defined in O and such that tJg)(k) (t) -. 0 as ItI - oo for all j, k. A sequence

in 5 converges to zero if and only if

IIT,,IIj,k - 0

(n -* oo)

2Note that U (resp. V)

must vanish fort < a (resp. fort < b). Theorem 3.2.1 is as well

valid for convergence (see Schwartz [1955: I]), but the present particular case is sufficient here.

8.2. Convolution, Tempered Distributions, Laplace Transforms

471

for all integers j, k >, 0, where

IIroIIj,k=

SUP

(l+ 1t1)'Iq)1')(t)I

(8.2.8)

0-<I-<k -oo<t<oo

The space S'(E) of tempered E-valued distributions consists of all linear

operators U, V,... from 5 into E that are continuous (that is, S(q)n) -* 0 in E

whenever qqn - 0 in S). As in 6D, a set Yu c 5 is bounded if r,,cp - 0 in S

whenever {q)n) is a sequence in X and the numerical sequence (en) tends to

zero. It is easy to see that `3C is bounded if and only if for any two integers

j, k there exists a constant Cj, k < 00 such that

IIPIIj,k<Cjk

(TE=X) (8.2.9)

Convergence of a sequence of distributions (Un) in 5'(E) is again defined as

uniform convergence on bounded subsets of S.

It is plain that a linear continuous operator from 5 into E is as well

continuous in the topology of 6D, since 6D c S and the inclusion map is

continuous. In other words, S'(E) c

6D'(E).3 Moreover,

a set 3C bounded in

6D is also bounded in S, thus this inclusion is also continuous. We can apply

to distributions in 5'(E) all the results in this section and in the previous

one. However, most of these results take a considerably simpler form when

applied to distributions in 5'(E). For instance Lemma 8.1.3 and Theorem

8.1.5 become global in eS'(E). In fact, we have

8.2.2

Lemma.

Let U E S'(E). Then there exists an integer p > 0

and a constant C > 0 such that

IIU(q))II < CIIq)IIP,P (p E g)

(8.2.10)

8.2.3

Structure Theorem.

Let U E S'(E). Then there exist two in-

tegers m, r > 0 and a continuous function f : R - E such that

U = f(m)

in R (8.2.11)

If(t)I=o(ItI') (It1_00).

(8.2.12)

The proof of Lemma 8.2.2 is entirely similar to that of Lemma 8.1.3

and will thus be omitted. To prove Theorem 8.2.3 we make use of (8.2.10) to

extend U to the space SP,P, where Sj,k is the Banach space of all k times

continuously differentiable functions defined in - oo < t < oc such that

I l9 l l j, k < oo, endowed with the norm HIM 4 Assume first that U has

support contained in t > 0, and let X be a Cfunction that equals 1 in

3 We are using here implicitly the fact that two distributions in 5'(E) that take the

same values in 6t must coincide. This follows from denseness of 6

in 5.

4An approximation argument of the type of Lemma 8.1.4 is used here.

472

The Cauchy Problem in the Sense of Vector-Valued Distributions

t >, 0 and vanishes in t < - 1, rt the function defined in (8.1.18). Then it is

not difficult to see using arguments similar to those in the proof of Theorem

8.1 that the E-valued continuous function

f(t)=U(X(s)'q(t-s)) (8.2.13)

satisfies (8.2.11) for m = p + 2. The verification of (8.2.12) follows from the

fact that the 11 - I I

p, n-norm

of X(9)71(t - s) grows no more than a power of t

as t - oo. Obviously, the argument extends to distributions U with support

in t>, a.

In the general case we choose an infinitely differentiable function

that equals 1 in, say, t > 0 and vanishes in t < - 1, write

U=U,+U2,

where U, = 4 U, U2 = (1- 4i) U and apply the previous particular case to U,

and to U2 defined by U2(((s)) = - U2(4p (- s)); if f f2 are the correspond-

ing continuous functions, then f(t) = f,(t)+(-1)mf2(- t) will be the func-

tion required in (8.2.11).

It results clearly from the proof of Theorem 8.2.3 that f may be asked

to vanish in t < a if U does. Note also that the following sort of converse

holds:

8.2.4

Lemma. Let U E 6D'( E ). Assume that U admits the represen-

tation (8.2.11), where f is a E-valued continuous function satisfying (8.2.12).

Then U E S'(E) (strictly speaking, U can be extended to a distribution in

S'(E))

The proof is rather simple and left to the reader.

We prove next that the spaces cS'(E) are closed under convolution.

We write S+(E) _ 6 +(E)n,5'(E); in other words, 5'(E) is the set of all

U E S'(E) with support bounded below.

8 . 2 . 5 T h e o r e m .

Let U E S' (E), V E S+(F). Then U* V E S' (G).

The proof is immediate. Let f, g be two E-valued continuous func-

tions vanishing for large negative t, growing no more than a power of t as

t --> oo, and such that

U=f(m)

V=g(n)inR.

Then, using the definition of convolution

U* V= (f *

g)(m+n)

in i,

where it is immediate that f * g grows at most like a power of t when t - 00

as well. Applying Lemma 8.2.4, the result follows.

We define now the Laplace transform of distributions in 50'(E) _

6D0'6D( E) n S'(E ). It will be convenient to introduce here some new spaces; we

8.2. Convolution, Tempered Distributions, Laplace Transforms 473

denote by 5'(E) the space of all distributions U in 6 '(E) with support in

t >, 0 and such that

exp(- wi) U E S'(E),

(8.2.14)

where w is a real number. The Laplace transform of U E S,,(E) is by

definition the function

U(A) = LU(A) = U(exp(- At))

=(exp(-wt)U)(exp(-(A-w)t)) (ReA>w). (8.2.15)

Formula (8.2.15) requires some explanation. Its right-hand side does not

make sense a priori, since exp( - (A - w) t) does not belong to 5 for any A.

We define it to mean V(X(t)exp(-(A - w)t)) (V= exp(- wt)U), where X is

any infinitely differentiable function that equals 1 in t > 0 and vanishes for

t < a < 0.

It is easy to show that this definition is independent of the

particular X used. Also, since S;, (E) c %.(E) for w < w', we may replace w

in (8.2.15) by any w'>, w; it can be immediately shown that this does not

modify the definition.

We begin by observing that CU, which is defined for ReA > w, is

analytic there. In fact, we have

h-'(LU(A+ h)-eU(A)) =

(exp(-wt)U)((p(t, A)),

where

p(t, A) = X(t)h-'{exp(-(A+ h - w)t)-exp(-(A- w)t))

-X(t)texp(-(A-w)i)ES.

We obtain as a consequence the familiar formula

(ReA>w)

(8.2.16)

(note that t U E S' (E) if U E %(E). Observe next that

V'(X(t)exp(- (A

- w)t))

=-V(X'(t)exp(-(A-w)t)-(A-w)X(t)exp(-(A-w)t))

_ (A - w)V(X(t)exp(-(A - w)t)).

Applying this to V = exp( - wd )U, we obtain the no less familiar equality5

LU'(A) = AEU(A) (ReA > w), (8.2.17)

where the left-hand side makes sense since U' E=- S' (E). Note finally that if

U E $ (E), then

exp(at)U E %' +a(E)

51f U coincides with a differentiable function f in t 3 0, we have U'= f'(t )+ S Of (0),

hence (8.2.17) becomes the classical formula Lf'(A) = xef(x)+ f(0).

474

The Cauchy Problem in the Sense of Vector-Valued Distributions

and

exp(- wt)(exp(at)U)(X(i)exp(-(A- to) 0)

=exp(-cot)U(X(t)exp(-(A-a-w)t))

for Re A > w + a so that

1(exp(ai)U)=(EU)(A-a) (ReX>w+a).

(8.2.18)

Let U E S; (E). Then exp( - w t) U E o (E) and, according to Theo-

rem 8.2.3, it admits the representation (8.2.11), where the function f satisfies

(8.2.12). Making use of (8.2.17) and (8.2.18), we obtain

LU(X) = e(exp(wt)(exp(- wt) U))

=am(ef)(A-w)

(ReA>co).

But I I(E f )(,\)I I < Cl I Re A I for Re X > 8 > 0. We obtain the following result:

8.2.6

Theorem.

Let U E S' (E ). Then there exists an integer m such

that

IIeU(X)II<C.,(l+IAI)m (ReX,w')

(8.2.19)

for any w'> w.

A partial converse of this result is

8.2.7 Theorem. Let h(A) be a function with values in E, defined and

analytic in Re X >, to. Assume that

IIh(X)II<C(1+IXI)`"

(ReX>,w).

(8.2.20)

Then there exists a (unique) U E 5)(E) with

h=CU.

(8.2.21)

Proof.

Clearly h must be analytic in an open region containing

Re X >, w. Define

At) =

/'w+tooextA-m-2h(A)

dA.

27ri

. - too

A deformation-of-contour argument shows that f (t) = 0 for t < 0; more-

over,

IIf(t)II <Cewt (t>0).

An easily justifiable interchange of the order of integration yields

(ef)(A) = A-m-2h(X )

Clearly f E S'(E). Then it follows from (8.2.17) that U= f(m+2) belongs to

eSW (E) and satisfies (8.2.21). It only remains to be proved that U is unique.

To this end, we observe that if U1, U2 are two distributions in 5W '(E) with

8.2. Convolution, Tempered Distributions, Laplace Transforms

475

the same Laplace transform,

then we have e f, (A) = A- m e U, (A) _

A-mLU2(A) = Lf2(A), where f,, f2 are the functions provided by Theorem

8.2.3; then f, = f2 by uniqueness of ordinary Laplace transforms and a

fortiori U, = U2.

We characterize next the Laplace transforms of certain distributions

with compact support:

8.2.8

Theorem.

Let U E P(E) with support in 0 < t < a. Then its

Laplace transform h(A) = CU(A) is a E-valued entire function and satisfies

Ilh(A)II<C(l+IAI)m

(ReA>0O), (8.2.22)

11h(A)II <C(1+

IAI)me-aRex

(Re X <0),

(8.2.23)

for some integer m. Conversely, let h be an E-valued entire function satisfying

(8.2.22) and (8.2.23). Then there exists a (unique) distribution U in l9'(E) with

support in 0 < t < a such that

h(A) =eU(A). (8.2.24)

Proof Let the support of U be contained in 0 < t < a. By virtue of

Remark 8.1.6, there exists an integer m and a continuous function f : R - E

vanishing in t < 0 and such that

U = f(m)

in R.

(8.2.25)

Since U = 0 for t >- a, f must be a polynomial of degree < m - 1 in t > a

(Lemma 8.1.1). Write f = f, + f2, where f2 = 0 in t < a, f, = 0 in t >, a. We

have

IIefi(A)II<C (ReA,0),

IIef(A)II<Ce-aReX

(ReA<0).

On the other hand, since f2 is a polynomial of degree < m -1 in t >- a,

Lf2(A) = e-laII(l/A), where II is a polynomial of degree < m. Inequalities

(8.2.22) and (8.2.23) then follow immediately from the fact that IU(A) _

AmLf(A)= Am(ef,(A)+E f2(A)), a consequence of (8.2.17).

Conversely, let h be an entire E-valued function satisfying (8.2.22)

and (8.2.23). As a consequence of the first inequality and of Theorem 8.2.8,

we obtain that (8.2.24) holds for some distribution U E ,o(E); conse-

quently, it only remains to be shown that U = 0 for t >, a. To see this, let f

be a continuous E-valued function vanishing for t < 0, growing no more

than a power of t at infinity and such that

U= P).

We may evidently assume that n >- m + 2. Clearly 1f( A) = A - "h (A) and by

virtue of the classical /inversion formula for Laplace transforms,

f(t) =

pw+iooeXtA-"h(A)

dA,

27x1

- ioo

476

The Cauchy Problem in the Sense of Vector-Valued Distributions

where w > 0. A deformation of contour then shows that if t > a,

.f(t) =

27Ii J_w

moo

eXtX-nh(X) A

d "'

+ (n

-1)!

()I(exth(x))

(w > 0),

where the second term on the right-hand side is a polynomial in t of degree

n - 1. As for the first term, observe that it does not depend on to > 0 and

that, by virtue of (8.2.23), if t > a the integrand tends to zero as to - co and

is uniformly bounded by a constant times (1 + IXI)-2. Letting to -+ oo, we

see that the integral vanishes and thus that f coincides in t > a with a

polynomial of degree < n - 1; a fortiori U = 0 in t > a, as we wished to

prove.

We observe that, in the proof of the direct part of the theorem, the

integers m in (8.2.25) and (8.2.22) may be taken to be equal.

and

8.2.9 Theorem. Let U E 5W(E), V E 5'(F). Then U * V E 5W(G)

e(U*V)(X)=i'U(x)eV(X) (ReX>w).

(8.2.26)

Proof If U E 6D (E) and V E 6D (F), then the formula

exp(at)(U*V)=exp(ai)U*exp(ai)V, (8.2.27)

valid for any a, can be easily verified. Making use of (8.2.27) for a = - to

and of (8.2.18), we see that we may limit ourselves to prove Theorem 8.2.8

in the case to = 0, where the fact that U * V E 50'(G) follows from Theorem

8.2.5. Let U E 50 '(E), ), V E So (F ), and let f (resp. g) be a E-valued (resp.

F-valued) continuous function growing at most as a power of t at infinity

and such that U = f (m) (resp. V = g(")) for two integers m, n. We use

(8.2.17) and obtain

{

L(U*V)=e((J

*g)(m+n))

_ xm+ne(f * g)

= xm(ef)(X)X"(eg)(X) = (W)(aOV)(X).

We have made use here of formula (8.2.26) for f and g; this can be proved

essentially as in the classical theory of Laplace transforms and is left to the

reader.

We close this section with a definition. For a > 0, let

Y.(t) -

(tom

r(a)

t < 0).

}

(8.2.28)

(