Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

8.4. The Cauchy Problem in the Sense of Distributions

487

Consequently inequalities (8.4.8) or (8.4.9) hold in the norm of (E, X) if

and only if they hold (with a different m) for 91(A) and A 91(X) in the norm

of (E; E). A similar statement holds if we change A 9t (A) by B 9t (X); if

either A or B are bounded, the estimate on 91(X) in the (E; E) norm

suffices.

We note that if (X2I - AB - A)-' exists and belongs to (E, E), it is

also bounded as an operator from E into X (we only have to apply the

closed graph theorem to the operators A 91 (A) and B 9t (X)).

8.4.7

Example. Let

P=8'®I-µ, (8.4.15)

where X C_ E and µ is a measure with values in (X, E); assume in addition

that

f °°Ilµ(dt)II <oo.

Here P (P) contains the half plane Re A >, 0 and

(A) = AI - f

Ce-srµ(dt)

(the precise extent of p(P) depends of course on µ). Equation (8.4.1) is the

integro-differential equation

DU(t)=µ*U(t)+F(t")

f`U(t-s)µ(ds)+F(t).

(8.4.16)

A particular instance is that where X = D(A) n D(B) (A and B as in the

previous example) and µ = S(t)®A+ S(t - h)®B for some h > 0; here

p(P) = C, $(A) = Al - A - e-""B, and (8.4.16) is the difference-differential

equation (or delay differential equation)

U'(t)=AU(t)+BU(t-h)+F(t).

The next theorem is a characterization of the class 50 1 n 6 '-. In

order to state the result, we introduce the following definition. A logarithmic

region in the complex plane is a set A of the form

A=A(a,/3)=(A; ReA>/3+alogIN1),

(8.4.17)

where a, /3 are two nonnegative numbers. (See Figure 8.4.1.)

8.4.8 Theorem. A distribution P E 5o((X; E)) is an element of

6D' ((E; X)) if and only if 9t (A) (A) -' exists in a logarithmic region A

and

II91(A)II(E,x)

C(1+IAI)'n

(AE=-A) (8.4.18)

for some C >, 0 and some nonnegative integer m.

488

The Cauchy Problem in the Sense of Vector-Valued Distributions

Proof. Denote by JCa the set of all functions in 6D that equal 1 in

0 < t < a and vanish in t >, 2a. Assume that P E 6) o((E;

X))- 1

and let

S = P-1. If T E 3Ca, it follows from (8.4.3) that

P*4pS=8®I- I, qpS*P=6®J-4Y,

(8.4.19)

where 4D=P*(1-T)S, 4'=(1-q))S*P. Since c=S(&I-P*q)S and pS

belongs to E to((E; X)), a fortiori to 50'((E; X)), it follows from Theorem

8.2.5 that P * q)S, thus also (D, belongs to S,0 '((E; E)); on the other hand, the

support of (1- qp)S is contained in t > a thus we obtain from (8.2.6) that

(D = 0 for t < a. We use then Theorem 8.2.3 to deduce the existence of a

(E; E)-valued continuous function f vanishing for t < a and growing at

most like a power of t at infinity, such that

iD = f(P).

Since f vanishes for t < a, we have

IIF-(D(X)11(E.E)<C'jXjPe-aRe11

(ReX

1). (8.4.20)

ReA=/3+alogJXJ

rl = (exp(2(?; - 0)/a) - t2)1/2

(a -- a Toga</3)

A(a,/3)

FIGURE 8.4.1

8.4. The Cauchy Problem in the Sense of Distributions

489

We choose now y, 0 < y < 1 and take N in a logarithmic region A(a, /3) with

a=p/a and /3, a-'log(Cy-') so large that A(a,/3) is contained in the

half plane Re X ,1 (see Figure 8.4.1). Then we deduce from (8.4.20) that

IIA)(X)II(E,E)<y

(XEA(a,$)).

(8.4.21)

On the other hand, since cpS E 50'((E; X)), we obtain from Theorem 8.2.6

that, if m is large enough,

IIe(TS)(t)II(E;X)<C'(1+IxI)m (ReX,1).

(8.4.22)

Taking the Laplace transform of the first equation (8.4.19) it follows that

$(X)E(00)=I-L(D(A).

(8.4.23)

We use (8.4.21) to deduce that (I - 1(X)) ' = E

A(a, /3) and

(b 1(X))" exists in

II(I-e (X))-'II(E

E)<(1-y)

(8.4.24)

there. Postmultiplying (8.4.23) by (I - '(X)) ', we see that 9i,(X) _

L(()S)(X)(I- L)(X))-' is a right inverse for $(X) in A(a, /3) and, in view

of (8.4.22) and (8.4.24), we have

IIR,(X)II(E,X)<C(1+IXI)m

(XEA(a,Q)).

(8.4.25)

We apply identical arguments to the second equation (8.4.19); we prove,

modifying if necessary the parameters a, /3, that (I -

exists and

belongs to (X, X) in A (a, /3 ). Taking the Laplace transform of the second

equation and premultiplying by (I - e we show that 31,(X) _

is a left inverse for $(X). It results that 91(X)

91r(A) = 9,(X)) exists and satisfies (8.4.18) in A(a, /3).

We prove now the converse. Assume the conditions of Theorem 8.4.8

are satisfied, let r be the boundary of the logarithmic region A(a, /3)

oriented clockwise with respect to A, and let p > m + 1 be a positive integer.

Define

Tp(t)

2I f

X-PeXt91(A)dX. (8.4.26)

7ri

The integrand grows no more than

at-P+m

as IX -> cc; thus TP is a

continuous (E; X)-valued function in

-o0<t<(p-m-1)/a

(8.4.27)

and a standard deformation of contour in the integral shows that TP (t) = 0

fort<0.

Since P E 50'((X; E)), there exists an integer q and a continuous

(X; E )-valued function f vanishing in t < 0, growing no more than a power

of t at infinity and such that

P = f (9). (8.4.28)

490

The Cauchy Problem in the Sense of Vector-Valued Distributions

We have

(f*TP)(t)=

JrX-Peat f`e-"sf(s)ds)91(X)A

(0 < t < (p - m - 1)/a), (8.4.29)

where the interchanging of order of integration is justified by the fact that

the integrand (of the double integral) grows at most like IAIa(t-s)-P+m when

I X I -f oo. Let now

n (X) = estf

°°e-'s f(s) ds.

We have

(IReXI-*oo).

It follows then from yet another deformation-or-contour argument that

1 f

2iri r

therefore the upper limit in the inner integral in (8.4.29) can be replaced by

oo. Doing this and making use of the equality $ (X) = Aa(L f)(X) that

results from (8.4.28), we obtain

(f *TP)(t) _

(_fxeX1dx)I

21ri

YP+q(t)I (0<t<(p-m-1)/a), (8.4.30)

where Ym is the distribution defined at the end of Section 8.2. If we define

SP = DPTP, the following equality results:

P*SP=S®I (t<(p-m-l)/a).

(8.4.31)

The convolution SP * f can be computed using essentially the same devices;

we obtain

SP*P=S®J (t<(p-m-l)/a).

(8.4.32)

Making use of (8.4.31), (8.4.32) of the arbitrariness of p and of the

"construction-by-pieces" Lemma 8.4.3, Theorem 8.4.8 follows.

Theorem 8.4.8 can be extended-if in a somewhat awkward form-to

the case P E 6 Do. In fact, let X = U

OX, Then we have

8.4.9 Corollary. Let P E 610'((X; E)). Then P E 6D ((E; X))-' if

and only if 4pP E 6%((E; X))

for all qq E'JC, that is, if pP satisfies the

hypotheses of Theorem 8.4.8 for all 99 E C.

Proof

Let p E Xa, a > 0. If pP E 61. o-', then there exists Sp E 610

with q)P*SP =B®I, Sq, *q7P=S®J. But(pP=Pint<a, so that P*S1,=

8.4. The Cauchy Problem in the Sense of Distributions

491

S ®I, ST * P = S (& J in t < a and Lemma 8.4.3 applies. Conversely, let

P E 6l-'

and let S = P-'. Then, if (P E 9Cu, we have q)P * TS = S®I - 0,

q)S * pP = S ®I - 4', where

0=S®I-q)P*pS

=-(1-q1)P*(l-rp)S+(l-p)P*S+P*(1-p)S

belongs to 50((E; E)) and vanishes for t < a; as for which admits a

similar expression, it belongs to S' ((X, X)) and vanishes in t < a. We can

then proceed just as in the proof of the first half of Theorem 8.4.8 to show

that 31 (A; pP) = $ (A; q?P) -' satisfies the assumptions there; hence cpP E

6D'-', as claimed.

8.4.10 Example. Assume E = X, B E (E, E).

(a) Let P(t) = 8'(i) 01 - S(t - h)®B. Then P E o n So-' and

S(i) = P-'(t")

=Y1(t)®I +Y2(i - h)®B + Y3(i -2h)®B2 +

the series convergent in So((E; E)). Here P (P) = C, 3(A) = Al - e-XhB,

r(P) is the set of all A such that AeXh e p(B) and 91 (X; P) = eAhR(AeXh; B);

in particular, r (P) includes the set (A;

I A I e h Re a >, r), where r is the norm of

B (or, more generally, its spectral radius). (See Figure 8.4.2.)

(b) Let P(t) = 8(t)®I + S'(t - h)®B. Then PE fo n 6Do-' (but not

to Sw ' for any w) and

S(t) = P-'(t)

=8(t)®I+8'(i-h)®B+8"(t-2h)®B2+

the series being convergent in 61. ' ((E; E)). We have p (P) = C, (A) = I -

Ae-11hB r(P) = (A; A-'ex' E p(B)), and 91(A) = A-leXhR(A-'euh; B). The

resolvent set r (P) includes the set (A;

I A I -'e h Re a >, r), r the spectral radius

of B. (see Figure 8.4.3.)

S(t)=S(t)®I+S(t"- h)®B+S(t-2h)®B2+

the series convergent in So. Again P (P) = C. Now we have $ (A) = I -

e-XhB, r(P) is the set of all A such that eXh E=-p(B) and 1t(A; P) =

eXhR(eXh; B). The resolvent set contains the half plane Re A > h-'log r.

(d) Let P = 8'(& I - p, µ a measure with values in (E; E) with

f llµ(dt)Il=w<oo.

Then P E Sw ' and

Y+t*µ*n

n=0

where * n indicates convolution powers. Here P (P) contains the half plane

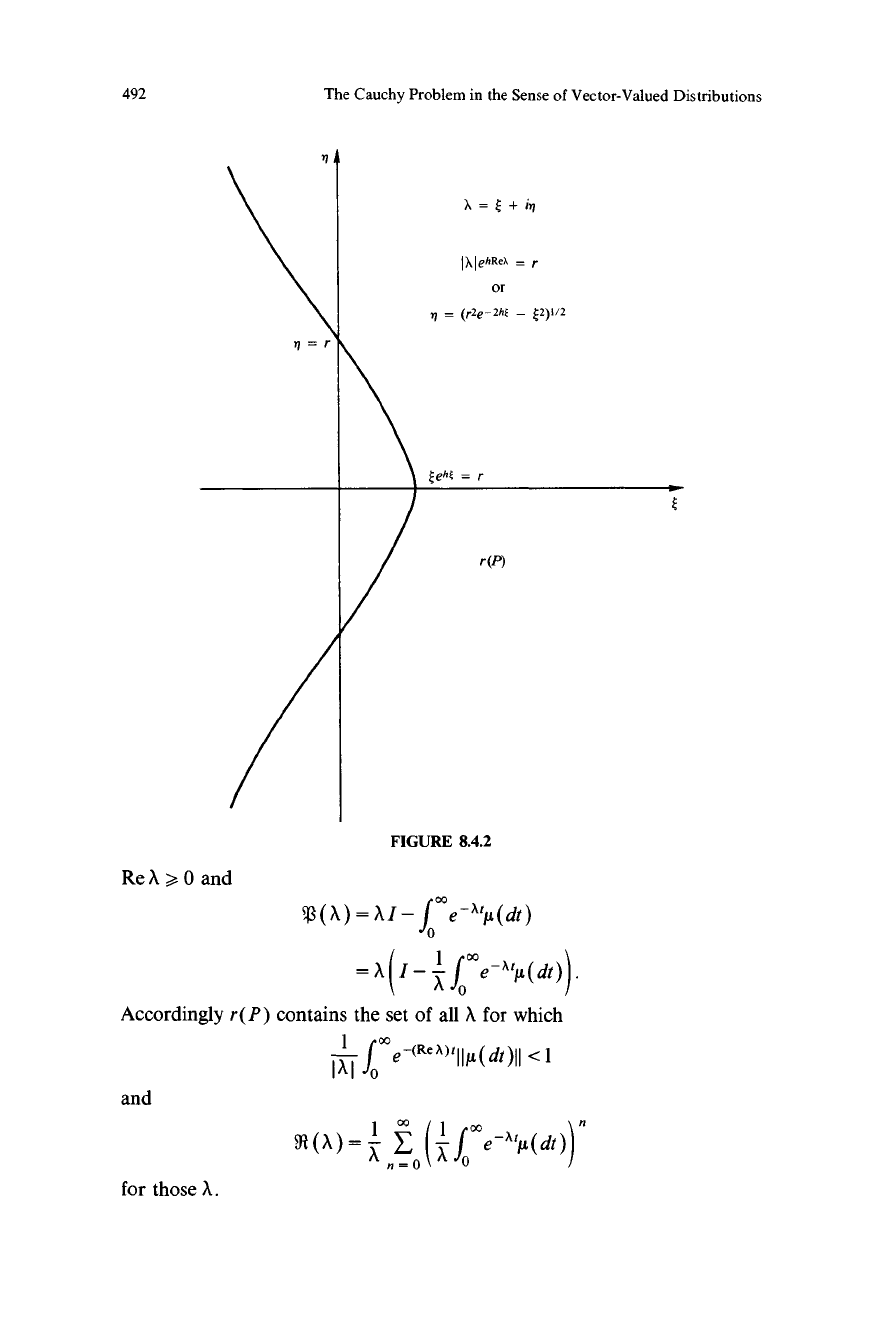
492

The Cauchy Problem in the Sense of Vector-Valued Distributions

),IeAReX = r

(r2e-2ht - 2)1/2

leht = r

r(P)

FIGURE 8.4.2

Re X >- 0 and

s(X)=xI-f e-atµ(dt)

=a(I- f 00e->,tµ(dt))

Accordingly r(P) contains the set of all A /for which

Ill

and

'(-f-e-"µ(dt))n

for those X.

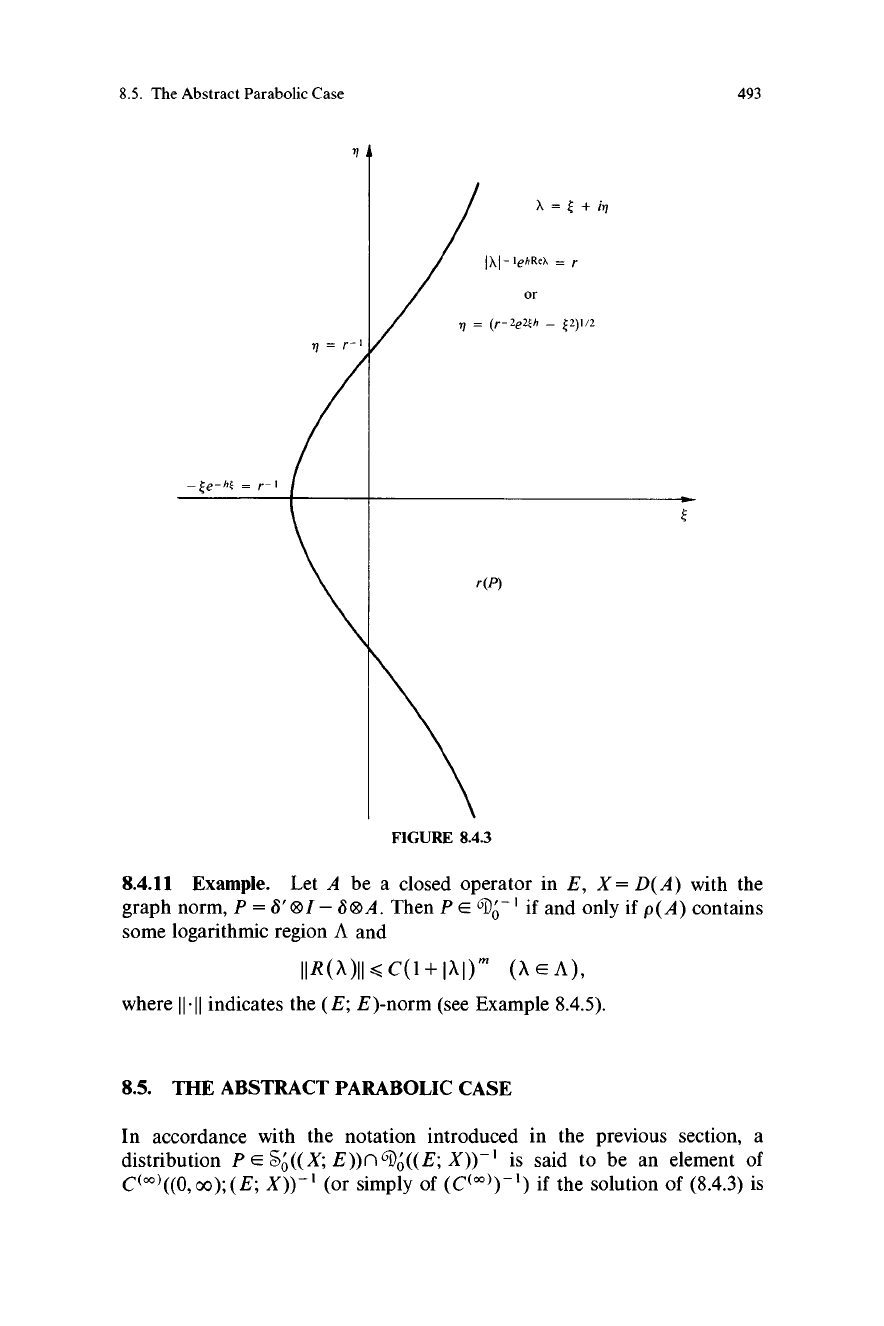
8.5. The Abstract Parabolic Case

493

X=E+hi

IXI-iehaeX = r

n = r-I

- te- ht = r-I

)1 =

(r-2e2th

2)1/2

r(P)

FIGURE 8.4.3

8.4.11 Example.

Let A be a closed operator in E, X = D(A) with the

graph norm, P = 8'(& I - 8 ®A. Then P E 6D'-' if and only if p (A) contains

some logarithmic region A and

IIR(X)II<C(1+IXI)'n (XEA),

where I I' I I indicates the (E; E)-norm (see Example 8.4.5).

8.5. THE ABSTRACT PARABOLIC CASE

In accordance with the notation introduced in the previous section, a

distribution P E 50'(( X; E))r)6D ((E; X))

is said to be an element of

C(°°)((0,oo);(E; X)) -' (or simply of (C(°°)) if the solution of (8.4.3) is

494

The Cauchy Problem in the Sense of Vector-Valued Distributions

an infinitely differentiable (E; X)-valued function in t > 0. In keeping with

the nomenclature introduced in Chapter 4, we call P abstract parabolic in

this case. We characterize the abstract parabolic distributions in &;o((X; E))

in the next result.

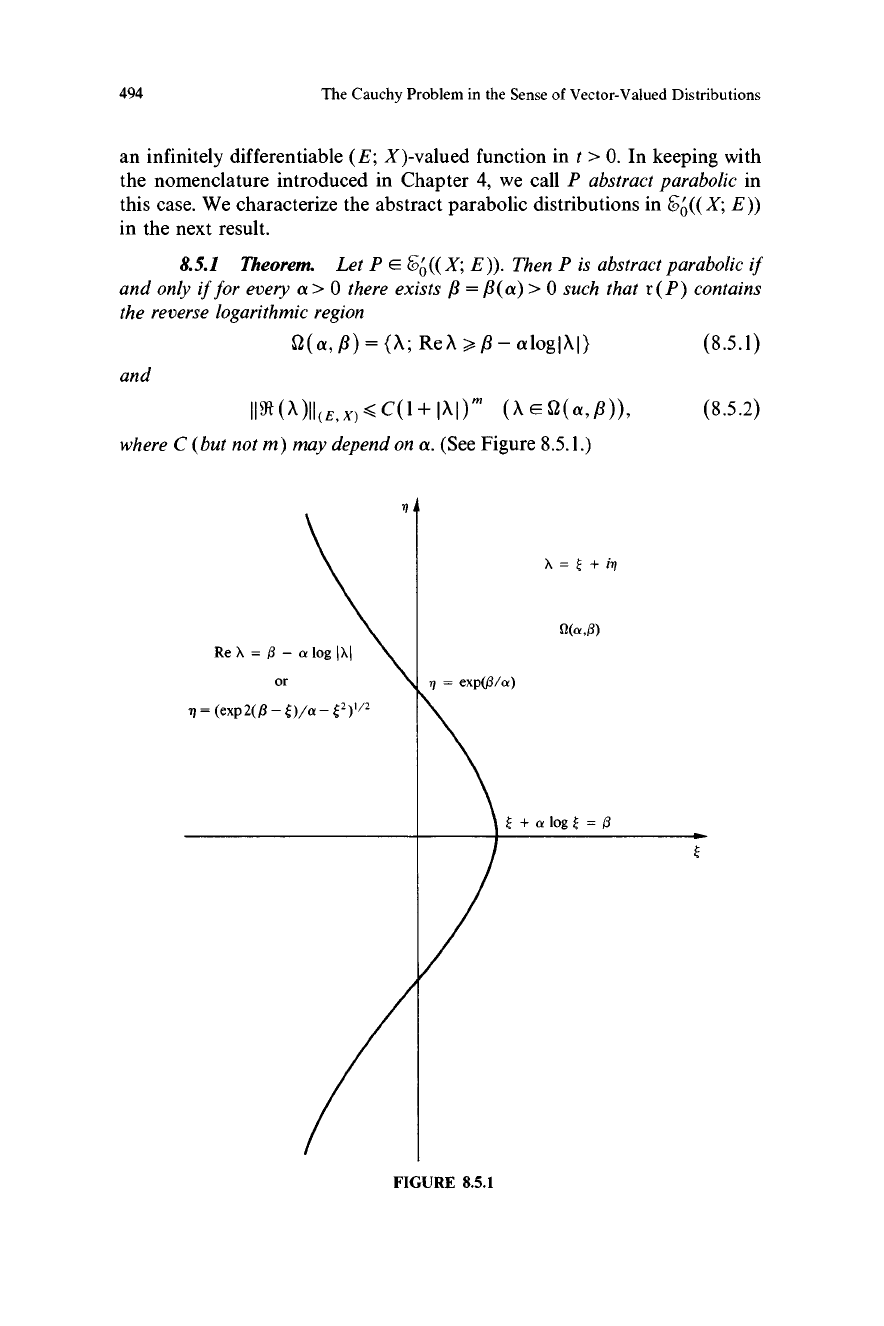
8.5.1 Theorem. Let P E 6;0'((X; E)). Then P is abstract parabolic if

and only if for every a > 0 there exists /3 = /3(a) > 0 such that r (P) contains

the reverse logarithmic region

2(a,/3)=(X; ReX>/3-alogIXI)

(8.5.1)

and

where C (but not m) may depend on a. (See Figure 8.5.1.)

ReX=(3-ologjXI

ort

r1=(eXp2(Q-S)/a-f2)1/z

= exp(/3/a)

9(a,Q)

f+alog f=/3

FIGURE 8.5.1

(8.5.2)

8.5. The Abstract Parabolic Case

495

Proof. Assume the hypotheses are satisfied. Then so are those of

Lemma 8.4.4 and P E S.((E; X))-' for some w > 0. Let S = P. We may

deform the contour of integration in (8.4.26) to E(a), boundary of S2 (a, #(a))

oriented in the same way as I'. The integrand in the resulting integral grows

no more that IXI

-at-p+m

as IXI - oo so that if t > (m + 1)/a we can

differentiate p times under the integral sign obtaining

S(t)= 1. f

eAt R(X)dX (t> (m+l)/a).

(8.5.3)

27x1

E(a)

Moreover, the same type of argument shows that (8.5.3) can be differenti-

ated n times under the integral sign if t > (m + n + 1)/a. Since a is arbitrary

this establishes that

is infinitely differentiable in t > 0.6

We prove the converse. Assume that S = P-' e C(°°)((0, oo); (E; X))

and that P E 60 '((X; E)). Let supp(P) c [0, b] and, given a > 0, choose

a > 0 and an integer p in such a way that

p>a(1+b), a<'-2, a<(1+b)/2p. (8.5.4)

Let rp E Xa. As in Theorem 2.5 we have

P*q)S=8®I-4D, q9S*P=8®I-41,

(8.5.5)

but now (D= P *(1- q))S = S®I - P * TS is an infinitely differentiable

(E; E )-valued function with support in a < t < 2 a + b, whereas 4, is a

(X; X)-valued function enjoying the same privileges. After repeated integra-

tion by parts, we obtain

LA(X) = x-p f

2a+be-xt(D(p)(t)

dt,

whence

IIL(D(A)II(E,E)<CIXI-p

(ReX

0) (8.5.6)

and

IIL")

(A)II(E,E)<CIXI-pe-(2a+b)Re?

(ReA<0).

(8.5.7)

Let 0 < y < 1. Choose /3 in such a way that every X E 0 (a, $) satisfies the

inequality

I X I % max(co,1)

with w = (C/y)'/p; then it follows from (8.5.6) that

IIL'D(x)II(E,E)<y

(XEQ(a,$))

(8.5.8)

(8.5.9)

6This half of Theorem 8.5.1 does not make use of the hypothesis that P E &o; it is

sufficient to assume that P E 5o.

496

The Cauchy Problem in the Sense of Vector-Valued Distributions

if Re A > 0. Taking /3 larger, if necessary, we can assume that

Ce-,8(2a+e)

< Y.

Also, by virtue of the first two conditions (8.5.4), we have

p > a(2a + b),

so that it follows from the last two estimates, from (8.5.7), and from (8.5.8)

that inequality (8.5.9) actually holds for all A E SZ (a, fl).

We write next qpS = S +((p -1)S and deduce that there is an integer

q independent of 9D such that for every (p E 3C there exists a continuous

(E; X)-valued function f9, vanishing for t < 0 and such that

q?S = f(q)

in R. (8.5.10)

Since pS = 0 for t > 2a, f! must be there a polynomial of degree < q - 1.

Proceeding now exactly as in the proof of Theorem 8.2.8, we obtain

IIe (ms)(X)II(E; X) <clXl4 (ReX 0, ICI ,1)

(8.5.11)

and

IIe(gS)(A)II(E;X)<CINIge-zaRea

(ReX<0, IXI>1).

(8.5.12)

Let A E 2(a, /3). We deduce from the first and third inequalities (8.5.4) that

-2a Re X < 2aa log IXI - 2a/3 < (a(1 + b)/p)loglXI - 2a/3 < loglXI - 2a/3

so that (8.5.11) and (8.5.12) combine to yield

Ile(9)s)(x)II(E;x)

<ClXlq+l

(AE0(a,Q)).

(8.5.13)

We make use now of (8.5.13) and of (8.5.9) in the style of Theorem 8.4.8 to

show that 91,(X) = E (pS)(X)(I - C' (X )) -' is a right inverse for $(X) in

SZ(a, /3) satisfying (8.5.2) for m = q + 1. The fact that Jl,(X) is a two-sided

inverse follows, again as in the proof of Theorem 8.4.8, from arguments of

the same type applied to the function ' in the second equality (8.5.5).

8.5.2

Remark. As a byproduct of the proof of Theorem 8.5.1, we have

obtained that a distribution P in (C(°°))-1 must be in S' ' for some w > 0.

But more is true: in fact, it follows from the representation (8.5.3) and a

simple estimation that there exists a w > 0 such that for every r > 0 there

exists a constant Ce > 0 with

IIS(t)II(E;x)<CEew`

(t,0).

8.5.3 Remark. Theorem 8.5.1 implies Theorem 4.1.3 on the characteriza-

tion of operators A in the class C°° (see the remarks on the relation between

the Cauchy problem in the strong sense and in the sense of distributions

after Theorem 8.4.1). To see that the estimate (8.5.2) can be strengthened to

(4.1.6), it suffices to notice that the integer q in (8.5.10) can be chosen equal

to zero in this case; although f, = TS is merely strongly continuous, the

argument works. The estimation must of course be carried out in the

(E; E)-norm.