Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

4.5. Second Order Partial Differential Operators. Assignation of Boundary Conditions

207

which, modulo a factor, is the derivative of u in the direction of the

conormal vector v = (a11,... ,

Eat,,, vj); naturally, D °u is called the co-

normal derivative of u at the boundary (with respect to A0). We also write

b= i

(

Dkajk)vj.

(4.5.9)

j1 k=1

The boundary terms in (4.5.7) can then be expressed thus:

Ref t (D"u)Iulp-2U+ pbluIP} do.

(4.5.10)

We shall use the following linear algebra result:

4.5.1 Lemma. Let d be a symmetric positive definite matrix. As-

sume that (CAE, ) = 0 for some E Rtm Then

The proof results immediately from writing in terms of a basis of

eigenvectors of d.

To study (4.5.7) we divide now the boundary IF into three disjoint

pieces:

r'= {xEF;(d(x)v,v)>0) (4.5.11)

r2= {xEF;(¢(x)v,v)=0,b(x)>0) (4.5.12)

r3= (xEF;(CT(x)v,v)=0,b(x)<0).

(4.5.13)

At F2 and r3 we have D"u = 0 for any u in view of Lemma 4.5.1 and the

first term in the integrand of (4.5.10) vanishes. The second term contributes

a nonnegative amount in r3 irrespective of any boundary condition satisfied

by u; to achieve the same in r2 we require that

u(x) = 0

(x E r2). (4.5.14)

Finally, the contribution over r' will be nonpositive if

u(x)=o (x E r') (4.5.15)

D°u(x) = y(x)u(x)

(x E r'), (4.5.16)

where y is a function with

y(x)+ I b(x),<0

(x E r1). (4.5.17)

We have proved part of the following result:

4.5.2

Lemma.

The restriction A of A, to the space of all functions

u E 6D

(2)(F2)

satisfying the Dirichlet boundary condition (4.5.14) on r2 and the

208

Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

r3; (Q(x)v,v) = 0, b(x) < 0.

No boundary conditions.

r2; (l (x)v,v) = 0, b(x) > 0

Boundary condition

u(x) = 0

FIGURE 4.5.2

boundary condition (4.5.15) or (4.5.16) in F3 is dissipative in Lp(l ),1 < p < o0

?(x)>,0

(xESZ), (4.5.18)

c(x)+i(Y_Y_DJDka,k(x)-Y_DJbj(x))<0 (xESZ),

(4.5.19)

and

y(x)+ p E(1 (x)-EDkaik(x))v, (x) <0 (x e I''), (4.5.20)

(where v(x) = (v ,(x),...,vm(x)) is the outer normal vector at x) if (4.5.16) is

used on t'. Condition (4.5.18) is necessary for dissipativity of any extension of

A0 in LP(SZ), I < p < oo; conditions (4.5.19) and (4.5.20) are necessary when

p = 1. Moreover, in this last case, the boundary condition (4.5.14) on Fz is as

well necessary for dissipativity.

The sufficiency proof has already been completed, at least when

p > 1, and is extended to the case p =1 by means of the usual limiting

argument. The necessity statements regarding (4.5.18) and (4.5.19) are

handled, just as in the previous section, by taking functions that vanish near

the boundary. Finally, the necessity of (4.5.20) for p =1 follows very much

as in the one dimensional case (note that the proof can be "localized" by

taking u with small and conveniently located support).

The case 1 < p < 2 presents the customary difficulties in that the calculation

(4.5.7) may not be directly justifiable for u E D(A0); we must then approximate an

arbitrary u E D(A0) uniformly together with its first two derivatives by a sequence

for which (4.5.7) is licit. We can do this by first extending u to a C(2) function u

in R"' with compact support (this can be easily handled by using a partition of unity

like (4.5.5)) and then approximating u as in the previous section.

Before studying the case E = C(F2) we examine the way A, trans-

forms under a smooth, invertible change of variables x -rl =,q(x). Denote

4.5. Second Order Partial Differential Operators. Assignation of Boundary Conditions

209

by A 1 the operator in the new variables,

m m

A1u= E E ajk(rl)D'Dku(q)+ Y_ b,(rl)D'u(rl)+j(n)u(rl),

j=1 k=1

j=1

(4.5.21)

where, using the traditional notation``for partial derivatives,

aX dx,,

(4.5.22)

ajk -

L a,K

axe axK

l=1 K=1

bj =

b` aXl

E a,,, dX2aX

c = c. (4.5.23)

L ,

L=1K=1

! K

Note that, if

E 118rr

EEj,kSjEk = EEajJjSk,

where

j =

(4.5.24)

so that the condition that d (x) >_ 0 is invariant. If the transformation

involves a piece of the boundary IF, then the unit outer normal vector

v = (v 1, ... , vm) at some point x E T and the unit outer normal vector

n = (n I__ , n m) at f1= rl (x) are related to each other by the equations

1nl

(4.5.25)

P 1nj=

axlva,

pvj=

a'qj

L=1 axj

where p = p(x) > 0 is a normalization factor; `then

P_2LLajknjnk = LLajkvjvk,

(4.5.26)

which shows that the definition of r,

is invariant as well. A simple

computation shows that, if

(4-

k=1

then

(4.5.27)

b = pb

at all points x E t where (Q (x) v, v) = 0. Hence r 2 and 1,3 are also in-

variant. Note that it follows from (4.5.22) and (4.5.25) that the conormal

derivative is invariant in the following sense:

D"u = EEajknj

a,n

PEEajkvj

aXk

= pD"u. (4.5.28)

210

Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

FIGURE 4.5.3

4.5.3 Lemma. Let A be the restriction of AI to the space of all

functions u E 61 (2)(SZ) satisfying the Dirichlet boundary condition (4.5.14) on

r2 and the boundary condition (4.5.15) or (4.5.16) on t'. Then A is dissipative

in C(R) if and only if

&(x)>-0, c(x)<0 (x(=-S2),

(4.5.29)

and

y(x)<0 (xEI'') (4.5.30)

if the boundary condition (4.5.16) is used on V. The boundary condition

(4.5.14) on I'2 is necessary for dissipativity.

We limit ourselves to proving the sufficiency part. Let u E D(A), u - 0

and m(u) = (x E SZ: I u(x) I = 11ull). We have to prove that

t(dx) 5 0Ref

m(u)

for any µ E 8(u); since u(x) t(dx) is a positive measure, it is enough to

prove that

Reu(x)-'Au(x),<0

(x E m(u)).

(4.5.31)

To prove (4.5.31) at points x E m (u) n 0, we use the argument in Lemma

4.4.1, thus only elements of m(u)n IF (which were absent there) may be

cause of trouble. Clearly m(u)n I'2 =0, but m(u) may contain points of r3

(and also of t ' if the boundary condition is (4.5.16)).

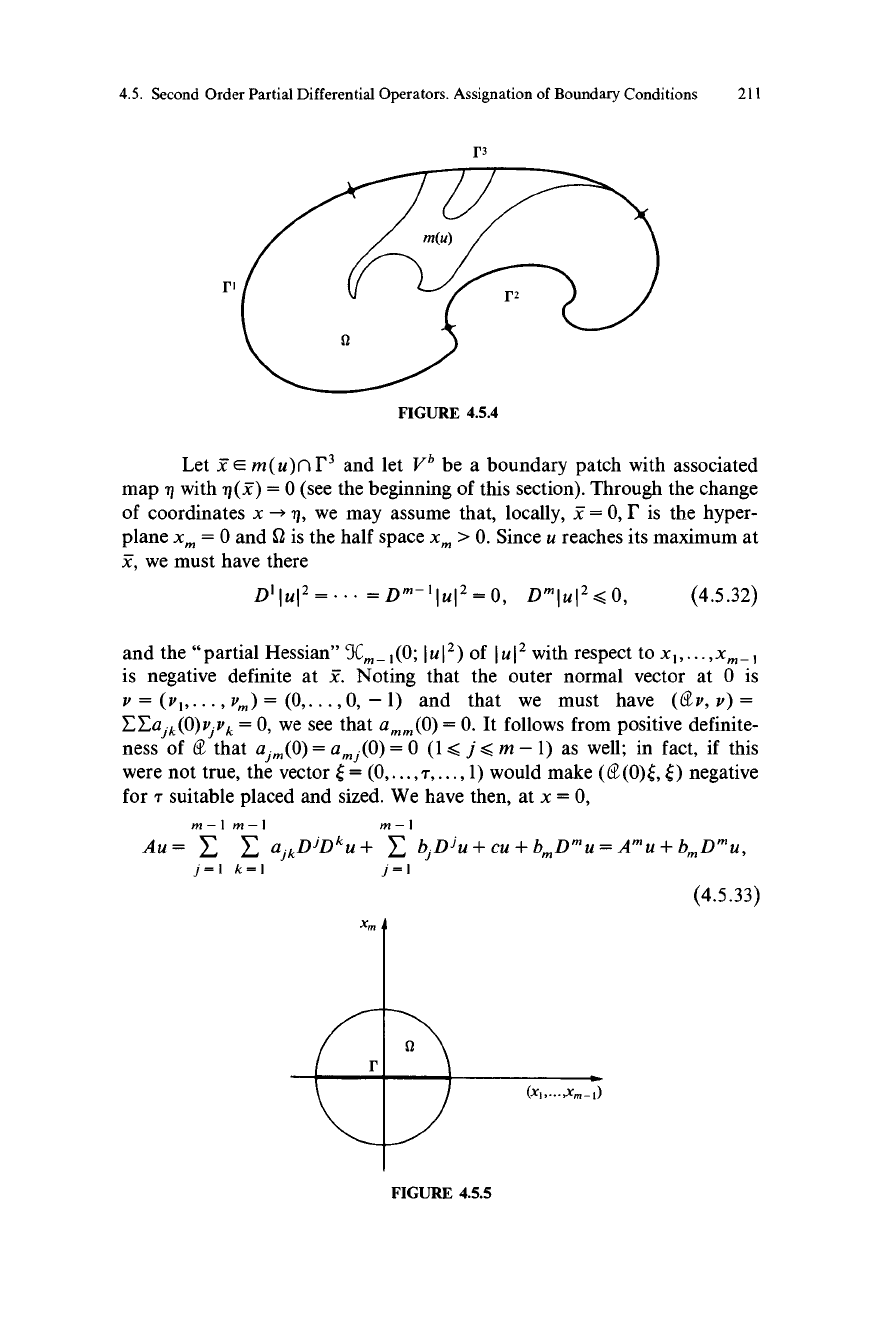
4.5. Second Order Partial Differential Operators. Assignation of Boundary Conditions 211

FIGURE 4.5.4

Let Y E m(u)flI'3 and let Vb be a boundary patch with associated

map 31 with n(Y) = 0 (see the beginning of this section). Through the change

of coordinates x - 71, we may assume that, locally, x = 0, I' is the hyper-

plane xm = 0 and 2 is the half space xm > 0. Since u reaches its maximum at

x, we must have there

D1Iu12=... =Dm-IIuI2=0

DmIUI2<0, (4.5.32)

and the "partial Hessian" X._#; I u 12) of I u 12 with respect to x,, ... , xm _ ,

is negative definite at X. Noting that the outer normal vector at 0 is

v = (P,,..., vm) = (0,. . . , 0, - 1) and

that we must have

(61 P, P) =

EEajk(0)vjvk = 0, we see that amm(0) = 0. It follows from positive definite-

ness of CT that a jm(0) = am j(0) = 0 (1 j S m - 1) as well; in fact, if this

were not true, the vector C = (0,..., T,..., 1) would make (d (0) E,

) negative

for T suitable placed and sized. We have then, at x = 0,

m - I m-1 m-I

Au= Y_ Y_ ajkD-'Dku+ Y_ bjDju+cu+bmDru=Anu+bmDu,

j=I k=1 j=1

(4.5.33)

FIGURE 4.5.5

212 Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

where Am acts only on x , ... , X.

_ Moreover, since 0 E r3, we must have

b(O) < 0, where, in the present coordinates, b = EDkamk - bm. Since (fi(x) is

positive definite, amm(x) > 0 everywhere and thus amm has a minimum at 0;

accordingly, D'amm = ... = Dm-'amm = 0, Dmamm i 0 there and

bm(0) = Dmamm(0)-b(0) > 0. (4.5.34)

We use now the decomposition (4.5.33) as follows. The first term involves

the (m -1)-dimensional operator Am and is treated as in Lemma 4.4.2 using

the first m -1 equalities in (4.5.32) and the negative definiteness of the

partial Hessian 9Cm

(0; I u 12 ). In the second term we use (4.5.34) together

with the relation

Re u-'Dmu = 111 U11

_2DmIU12

and the last inequality (4.5.32); adding the two terms we obtain (4.5.31)

at x.

The preceding argument settles completely the problem if the

Dirichlet boundary condition is used in r', since in that case

m(u)n(r' u r2) =0.

(4.5.35)

Clearly, we can also cover the boundary condition (4.5.16) if we show that

(4.5.30) implies (4.5.35), which we do now. Since we already know that

m(u)fl r 2 =0, we only have to examine the case where x E m(u)r) F'. If

y(.) < 0, we have

D"Iu12=2Re uD°u=2y1u12<0

(4.5.36)

at X. Since (dv, v) _ (PP, v) > 0 there, the conormal vector points away from

I (at least locally); hence (4.5.36) implies that u must be increasing along

- P near x, a contradiction. If y(x) = 0, however, this simple argument

breaks down (and (4.5.35) may in fact be false). To handle this case, using

again a boundary patch V' and the associated map q we can assume locally

that x = 0, r is the hyperplane xm = 0, S2 the half space xm > 0. Since x is a

maximum of I u 1 2 , Di I U12(X) = 0 (1 < j < m -1), but in this case it is also

true that

FIGURE 4.5.6

4.5. Second Order Partial Differential Operators. Assignation of Boundary Conditions

213

D''Iu12=2Re iW u=0

at 0 and, since (9 P, v) > 0, v does not belong to the hyperplane xm = 0;

hence all the first partials of I u 12 vanish at x = 0:

D'Iu12=... =Dm1u12=0.

(4.5.37)

We make use of Maclaurin's formula up to terms of order two,

Iu(x)12=1u(0)12+z(`x(0; Iu12)x,x)+o(Ix12)

in the half space xm > 0. Since 0 is a maximum of

I u 12, we must have

(JC (0, 1 u 12) ,

) < 0 in the half space

>, 0, thus in R m, and we can handle

x exactly as a point of m (u) n 9. This ends the proof.

The necessity arguments are conducted much as in the one-dimen-

sional case (Lemma 4.4.3) and are left to the reader (Example 4.5.5).

As we did in last section, we translate the conditions obtained to

operators in divergence form. Condition (4.5.19) is (4.4.17); the definition of

b is now

b = Y- bi vi (4.5.38)

i=1

and (4.5.20) accordingly becomes

y(x)+ p Y- Li (x)vi < 0. (4.5.39)

We bring into play the formal adjoint Ao defined in the previous

section (see (4.4.14)). The Lagrange identity (4.4.15) takes the form

f(Aou)vdx= fu(Aav)dx+ f((D°u)v-uD''v+buv)dx,

(4.5.40)

where b is given by (4.5.9) and u, v E 6 D(

2 ) ( 0).

Assume, for the sake of

simplicity, that r' = F (i.e., that (9 (x) P, v) > 0 for x E F). If u satisfies the

boundary condition (4.5.16), then

f(Aou)vdx= fu(Aov)dx (4.5.41)

if v satisfies the adjoint boundary condition

D'''v(x) = (y(x)+b(x))v(x)

(x E T'). (4.5.42)

On the other hand, (4.5.41) holds if both u and v satisfy the Dirichlet

boundary condition, which is thus its own adjoint.

214

Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

4.5.4 Example.

Show that (4.5.20) is necessary for dissipativity in L'(2)

of the restriction of A, satisfying (4.5.16) on F. Show that the Dirichlet

boundary condition (4.5.14) on I'2 is as well necessary.

4.5.5 Example.

Show that (4.5.30) is necessary for dissipativity in C(SZ)

of the restriction of A, satisfying (4.5.16) on I''. Show that the Dirichlet

boundary condition (4.5.14) on r2 is as well necessary.

4.6.

SECOND ORDER PARTIAL DIFFERENTIAL

OPERATORS. CONSTRUCTION OF m-DISSIPATIVE

EXTENSIONS IN L2

We consider operators in divergence form

m m m

Aou= E Y_ Dj(ajk(x)Dku)+ E bj(x)Dju+c(x)u

(4.6.1)

i=1 k=1

J=l

in an arbitrary domain 9 in Euclidean space 118 m (to simplify notations the

coefficients bj in (4.4.2) are called bj here). A great part of the theory can be

constructed without smoothness assumptions on the coefficients, thus we

shall only suppose that the ajk, the bj and c are measurable and bounded in

I. In this level of generality, of course, the first difficulty is how to define

D(Ao) (even if u E 6D(S2),EajkDku may fail to have weak derivatives). We

shall avoid this problem simply by not using A0 in the general case (if the

coefficients fulfill the differentiability assumptions in the previous two

sections we set D(A0) ='Dt2t(S2).) Besides the measurability assumption, we

require that A0 be uniformly elliptic:

(A) There exists K > 0 such that

L L ajk(x)SjEk i

K1t

(

Rm)

(4.6.2)

a.e. in S2.

Since conditions (4.5.19) and (4.5.20) for boundary conditions of

type (I) are far from necessary for p = 2, we shall discard them and content

ourselves with constructing from A0 operators A in C+(1, w) (i.e., such that

A - wI is m-dissipative) for some w.

All the subsequent treatment is based on:

4.61 Lemma.

Let H be a complex Hilbert space and let the func-

tional B : H X H -> C be sesquilinear (linear in the second variable, conjugate

linear in the first). Assume that

I B(u, v)I < Cllull llvll>

I B(u, u)I > cIIuI12

(u, v E H) (4.6.3)

for some c, C > 0. Then if 4) is a bounded linear functional in H, there exists a

4.6. Second Order Partial Differential Operators

215

unique uo E H with C-'II(DII < IIuoII < c-'II4 II and such that

*(u) = B(uo, u). (4.6.4)

Proof.

It follows from the first condition (4.6.3) that v - B(u, v) (u

fixed) is a bounded linear functional in H. Therefore, there exists w = Qu

such that

B(u, v) = (w, v), (4.6.5)

() the scalar product in H. It is clear that the operator Q so defined is

linear in H. Moreover, IIwI12 = IIQuI12 = (Qu, Qu) = B(u, Qu) = IB(u, Qu)I

< CIIuIIIIQuII so that Q is bounded (with norm < C). On the other hand,

IIuIIIIQull % I (Qu, u)I = IB(u, u)I % cIIuI12 so that IiQull % cllull; hence Q maps

H in a one-to-one fashion onto a closed subspace K of H. If K * H, there

exists a nonzero wo such that B(v, wo) = (Qv, wo) = 0 for all v E H. But then

B(wo, wo) = 0, which contradicts the second inequality (4.6.3). It follows

that K = H and that Q is invertible. If vo E H is such that 1(u) = (vo, u),

we have

4D (u) = B(Q-'vo, u),

which shows (4.6.4). The statements on the norm of uo = Q-'vo are obvious

from the previous argument.

We look now at the problem of obtaining extensions (properly

speaking, "definitions") of A0 that belong to e+(1, w). These extensions will

be obtained on the basis of boundary conditions /3 of one of the following

types:

(I)

Du(x)=y(x)u(x) (x E F)

(4.6.6)

(II) u(x)=0 (xEF) (4.6.7)

already considered in Section 4.5. As we may expect, these boundary

conditions will only be satisfied in a suitably weak sense.

We begin with the Dirichlet boundary condition (4.6.7). The basic

space in our treatment will be the closure H01(2) of 6 (S2) in H' (S2) (see

Section 8 for definitions); as usual, H'(2) and Ho(S2) are equipped with the

scalar product

(u,v)H'(st)= (u,V)LZ(9)+ (Diu,Div)L2(st)

(4.6.8)

For X >, ess sup c + 1 we define

(u, v);, = (X - c(x)) uv) dx. (4.6.9)

It is easy to see that each possesses all the properties of a scalar

product; moreover, the norm II' IIa derived from ( , )a is equivalent to the

216 Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

norm provided by (4.6.8). In fact, assuming (as we may) that K < 1 in (4.6.2),

we obtain

KIIUIIH.(a) < IIUI12 < MIIUIIJJ (a)

(u E H01(S2)), (4.6.10)

where M is a constant depending on X, on the ask and on c (recall these

functions are bounded in Sl). We define a sesquilinear form in H01(Q) by the

formula

BA(u,v)=

f(EbjDJu)vdx. (4.6.11)

Assume that

A - c(x) >, K > 0 a.e. in 12, (4.6.12)

where K is to be fixed later. Then

fa(EbjDJu)vdx

fI(YbjD'u)vdx

(f(x_C(x))-1IEbjDju12dx)1'2

(f(x_c(x))IvI2dx)1/2

< CK-1/2(EIID'uIj)IIvIIk <

Cm1/2K-1/2(EIIDJuII2)1/2IIvII,

<CM

1/2K-1/2IIuIIHa(a)IIvIIA<C'K-1/21IuIIXIIVIIX

(u,vEHH(SZ))

(4.6.13)

by the Schwarz inequality, where K is the constant in (4.6.12) and C' does

not depend on X. Taking K sufficiently large, we may assume that

C'K-1/2 = a < 1 so that

a(EbjD'u)udxReBa(u,u)=IIuIIa-Ref

(1-a)IIuIIA

(uEHo(Z))

(4.6.14)

and the second inequality (4.6.3) holds for Ba; that the first is verified as

well follows from the Schwarz inequality for (, )k and from (4.6.13) for

anyK>0.

We define now an operator A($) in L2(S2) as follows. An element

u E L2( 2) belongs to the domain of A if and only if u E Ho (S2) and

w -+ Bk(u, w) is continuous in HH(&) in the norm of L2(S2). Since Ho(2) is

dense in L2(S2), we can extend the functional w - X (u, w)- Bju, w) con-