Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

4.1. Abstract Parabolic Equations

177

FIGURE 4.1.1

the usual way that extensions to overlapping disks coincide in their intersec-

tion, we see that S can be analytically extended to the open sector

2+(9'-)=

<q'=aresin(Ce)-t;

- 0).

Let 0 < 9)'< cp, EI I K. S cos qp', (p"= arg

so that t =I

I /cos (P"

,<I

I /cos rp' < Sand (4.1.10) holds. We have

=CO+

(Cn sin g)rr)

n=1

n! .

n-1

C° + C' F

(Ce

sin

qp') n

< C + C"

sin 99'

(4.1.14)

n=t

1-Cesinq)''

FIGURE 4.1.2

178

Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

An estimate of the same sort can be obtained in ICI < a for arbitrary a using

the semigroup equation (4.1.8).

We prove now strong continuity of S. Since IIS(s' )II is bounded in

E+((p') for ICI bounded, we only need to show continuity for, say, u E D(A).

We note first that if u e D(A), then

E+(q)).

(4.1.15)

In fact, this is clearly the case for

= t > 0 and follows for 2+(q)) by

analytic continuation. Together with (4.1.14), this implies that IIS'Q)ull is

bounded in

for

bounded. We write

(uED(A)). (4.1.16)

We have

II(SM - SUI))ull < f IIS'(z)ull IdzI <CIA-

in view of the boundedness of

We obtain

IISM u-ul1 <CI - W IIIu1I+IIS(IM u - ull,

which, in view of the strong continuity of S(t) for t real implies the desired

result.

We prove now the converse. Assume that A E 9 ((p -) for some

(p > 0. Then, if p' < ip we have

AS(t) = S'(t)

1 S(z)

= 21ri

dz (4.1.17)

Iz-tI=tsinq)'(z-t)

from which (4.1.10) readily follows.

4.1.6 Remark. Making use of the argument at the end of the proof of

Theorem 4.1.5 we can prove that

EICI < a)

(4.1.18)

if a > 0, q)'< T (the constant C, of course, will depend on qp' and a). In fact,

we only have to apply Cauchy's formula (4.1.17) for t = E I+(T) integrat-

ing over circles

I z - I = I

I sin rl, where rl < T - T'. (See Figure 4.1.3).

4.1.7 Remark.

Although we may allow the parameter q) in the definition

of 9(q)) to roam in the range 0 < q, < fr, it should be pointed out that the

class 9, (q)) becomes trivial when qq > it/2; precisely,

l(q) _ (E)

(9,> 1r/2).

(4.1.19)

In fact, let be analytic in a region 2+(q)) with q> > 1r/2. Making use of

the semigroup equation (4.1.8) we can write

S(E)=S(E+i)S(E-i)

(a>O).

If we let a- 0,S(E+i)-*S(i),S(E-i)-*S(-i)in (E) so thatS(E) - I in

(E). This shows, using Lemma 2.3.5, that A is bounded, thus proving

4.2. Abstract Parabolic Equations; Analytic Propagators

FIGURE 4.1.3

179

that equality (4.1.19) holds.

Using the argument in Theorem 4.1.5 we easily obtain:

4.1.8 Theorem.

Assume A E i3°° and

limsuptllAS(t)II <

= 0.367...

(4.1.20)

t-0+ e

Then A is bounded. The constant 1/e in (4.1.20) is best possible.

That 1/e is the best possible constant is seen as follows: let 12 be the

Hilbert

space of

all sequences

'1 = {q,, 112,........

rl" E C) such that E I " 12 < oo endowed with the scalar product

7- ,M ,, and let A be the self-adjoint operator defined by A _ (-

Then

A E (2°° with S(t)d = (e-"tE") and limsup tIlAS(t)II =1/e.

4.1.9 Example.

Let A E C' n C'°°. Then A is bounded.

4.1.10 Example. LetA E G'°°. The assumption that is integrable

near zero for every u E E does not imply that A is bounded (compare with

Example 4.1.4). This can be verified with the same operator in Example

2.4.7, this time in the Banach space of all sequences I, E2, ...) such that

I < oo, endowed with the norm II' ll

4.2. ABSTRACT PARABOLIC EQUATIONS;

ANALYTIC PROPAGATORS

We give in this section a complete characterization of operators in the class

d in terms of the location of p (A) and the growth of II R (X )I I

there. This

characterization turns out to be fairly simple to apply, involving only the

180 Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

verification of a single inequality for IIR(A)U in contrast to the infinite set of

inequalities (2.1.11) that appear in connection with the class (2+.

Extending our definition in the previous section, we set, for a real,

2+(p,a)_{A; Iarg(X-a)I<(p,X*a)

2+(-p -,a)=(a; Iarg(X-a)I<(p,X*a).

4.2.1 Theorem.

Let A be a densely defined operator in E, and let

0 < T < 77/2. (a) If A E &,(99) then there exists a real number a such that

2+(T'+ 7r/2, a) c p(A) for each p' (0 < T'< (p) and there exists C = C., such

that

IIR(X)II <

IX - al

(4.2.1)

for A E I+(qg'+ it/2, a). (b) Conversely, assume that 2+(q) + Ir/2, a) c p(A)

and that (4.2.1) holds for X E I+(q) + 7r/2, a). Then A E & ((p - ).

Proof

Let A E d (T). If w is the constant in (4.1.9), let a = w/cos cp

and Aa = A - aI, so that Aa) =

Since Red > cos

in M (qq ), we have

Ce-aRer+wj1' < C

(4.2.2)

Hence

R(A)u = R(X - a; Aa)u

= f °°e- 1'-alSa(t)udt (uEE) (4.2.3)

for Re(X - a) > 0. If Re(X - a) e'q' > 0 as well, we can deform the path of

integration in (4.2.3) into the ray r

_ =

arg = - 4p, Re > 0) and thus

extend analytically R(X) to the half plane Re(X - a)e'9' > 0. Likewise, if

Re(X - a) > 0 and Re(X - a)e-4 > 0, we can integrate in the ray T+ =

arg = q', Red' >, 0) and extend R (X) to the half plane Re(X - a) a-'' > 0.

That these extensions are in fact R(X) in the new regions follows from

Lemma 3.6. We have then proved that R(X) exists in 2+(q) + 1r/2, a). We

estimate now IIR(X)II. If Re(A - a)e'9' > 0, we obtain, bounding the integral

in r-, that

IIR(X)II<C f 00 exp{-(Re(X-a)e'9)t)dt

=C/Re(X-a)e'9' (Re(X-a)e'9'>0). (4.2.4)

Similarly, if Re(X - a)e-'' > 0, we integrate in T+, obtaining

IIR(X)II<C/Re(X-a)e-'P (Re(X-a)e-'9'>0).

(4.2.5)

Inequality (4.2.1) then results from the easily verified estimates

X - aI < Re(X - a) e'q/sin(T - T')

(-((p'+ir/2)<arg(X-a)<0)

(4.2.6)

4.2. Abstract Parabolic Equations; Analytic Propagators

181

FIGURE 4.2.1

and

I A -aI< Re(A-a)e-'P/sin(qp -qp')

(0<arg(A-a)<q'+.r/2)

(4.2.7)

valid if qq - p < 1r/2- qv. (The constants in (4.2.1) and (4.2.2) are of course

different; the same observation applies to subsequent estimates.)

We prove now the

converse.

Suppose

that R (X)

exists in

1+(q9 + 17/2, a) and let (4.2.1) hold. By means of a translation of A similar

to the one used in the first part of the proof, we may and will assume that

a < 0. Let 0 < T

I , T2 <

q, and let I'((p , T2) be the contour consisting of the

two rays arg A = T I + 17/2, Im A >, 0, and arg A = - (q72 + fr/2), Im A < 0,

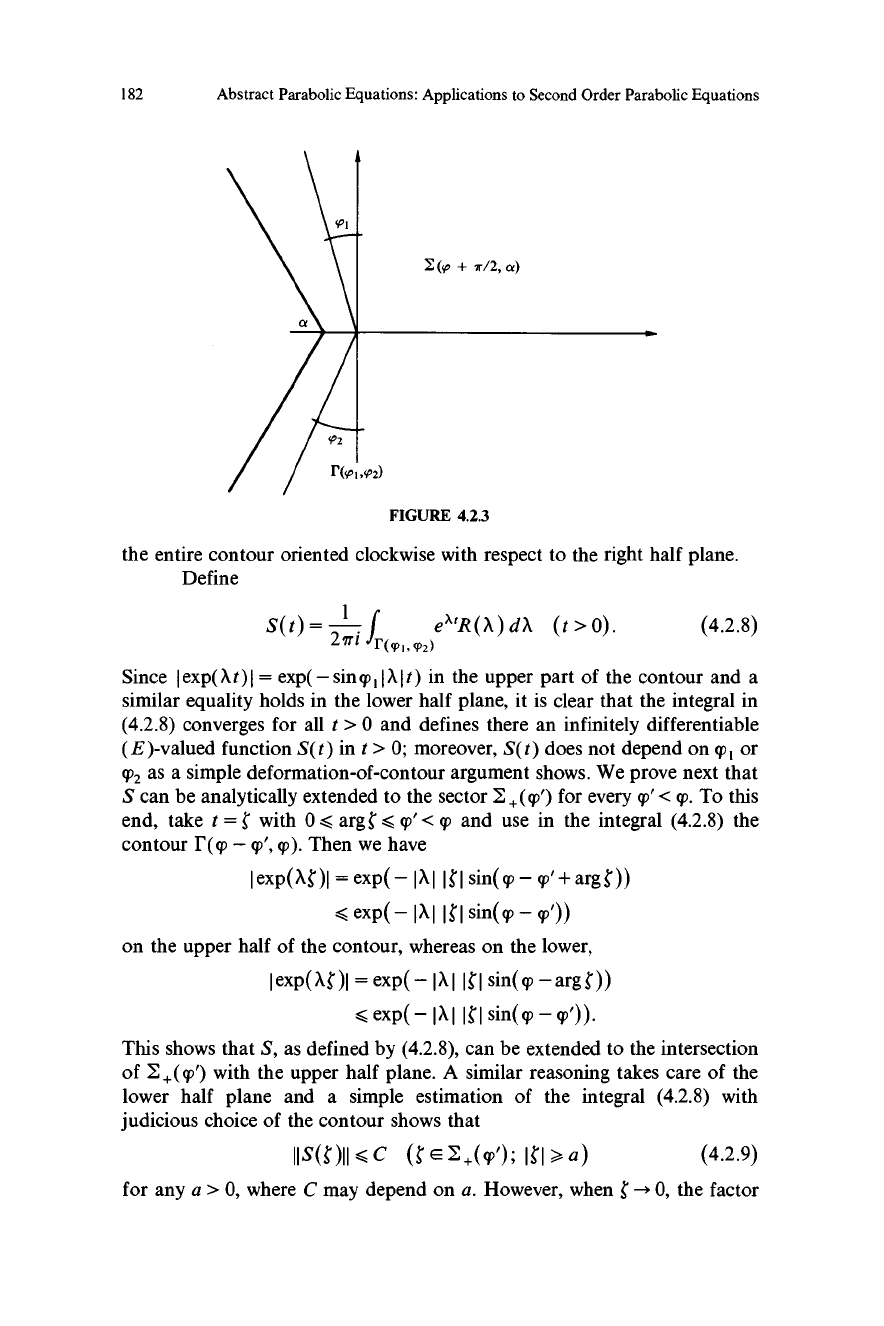
182

Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

FIGURE 4.2.3

the entire contour oriented clockwise with respect to the right half plane.

Define

S(t) = -

f,roz)eatR(X) A (t

> 0).

(4.2.8)

r(ro 1Since

I exp(X t) I = exp(- sin qg, I A I t) in the upper part of the contour and a

similar equality holds in the lower half plane, it is clear that the integral in

(4.2.8) converges for all t > 0 and defines there an infinitely differentiable

(E)-valued function S(t) in t > 0; moreover, S(t) does not depend on q,, or

T2 as a simple deformation-of-contour argument shows. We prove next that

S can be analytically extended to the sector 2+(T') for every p' < 99. To this

end, take t = with 0 < arg < (p' < 9) and use in the integral (4.2.8) the

contour T(4) - q)', 99). Then we have

IeXp(X )I = exp(- IxI ICI sin(p - T'+arg ))

< exp(- IxI ICI sin(gc - p'))

on the upper half of the contour, whereas on the lower,

IeXP(X )I = exp(- IxI ICI sin(p -arg '))

exp(- Ixi ICI sin(q) - p')).

This shows that S, as defined by (4.2.8), can be extended to the intersection

of 7-+((p') with the upper half plane. A similar reasoning takes care of the

lower half plane and a simple estimation of the integral (4.2.8) with

judicious choice of the contour shows that

C ( E

ICI >- a)

(4.2.9)

for any a > 0, where C may depend on a. However, when - 0, the factor

4.2. Abstract Parabolic Equations; Analytic Propagators

183

in the integral (4.2.8) dissolves away and we need to bound in a

different way. To do this, we take first with 0 < arg < qq', x 0, and use

the contour T(pp - q7', co in the integral in (4.2.8). After this we make the

change of variables z = X , obtaining

SM = 1 f eZ

( z )

dz, (4.2.10)

217i

where of course I'(qq - , T) = T(qg - T'+ arg (p - arg ). We can now

deform the contour to, say, F(qq, qp - q)') and modify this contour in such a

way that z passes to the right of the origin as it travels upwards. Call t' the

contour thus obtained.

FIGURE 4.2.4

We make use of (4.2.1) to estimate the integrand in (4.2.10); there

exist a, C' > 0 such that if

I I < a,

(z) I<Cz-,-a

<C'

fI (zEI")

(4.2.11)

(note that if z E T' and 0 < arg < qq', then z - E 2+(T + 17/2, a)). We

obtain

IISMII <C'fr,

IdzI. (4.2.12)

A symmetric argument takes care of the range - qp' < arg < 0; we finally

deduce that

EZ+((p'), ICI<a)

(4.2.13)

We show next that S is strongly continuous at the origin, that is,

lim

(uEE)

(4.2.14)

184

Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

for every q)'< (p. In view of (4.2.13) we only have to prove this for u in a

dense subset of E, say, in D(A). As customary we treat separately the cases

0 < arg < qq' and - q,' < arg < 0. In the first case we use the contour

I'(q) - qq', p) modified near the origin in the same way as r, (we call I"

again the resulting contour). Making use of the equality R (X) u =

A-'R(X )Au + X-'u in the integral (4.2.8), we obtain

2Iri f e'tR(X)udX

eX 1 e

217i

21ri J

-dX u.

r r

The first integral is continuous in I(q)) and vanishes at

= 0, as can be

seen making use of (4.2.1). The second one can be readily computed by

residues and evaluates to 1. This shows that (4.2.14) holds.

We have proved, in particular, that

is strongly continuous in

t >- 0 and it follows from (4.2.13) that

IIS(t)II<C

(t>-O)-

To show that A E (2+, we use now Lemma 2.2.3. Let 0 < q'' < 4p,

r _

r(q)', (p'). If µ > 0 and u E E, we have

f 00e-µ`S(t)udt= f e-µ`(

1 f

0 0

27ri r

21ri fr(J0

R(A)udA

i r tut

=R(µ)u,

(4.2.15)

where the interchange of the order of integration can be easily justified

estimating the integrand, and the last step is an application of Cauchy's

formula in the region to the right of I', which is clearly valid in view of

(4.2.1). This ends the proof of Theorem 4.2.1.

Theorem 4.2.1 can of course be cast in the form of an equivalence.

4.2.2 Theorem. Let A be a densely defined operator in E, 0 < (P <

Ir/2. Then A E d (qq -) if and only if for every q)' < qp there exists a real

number a = a(q)') such that 2((p'+ ¶r/2, a) c p(A) and (4.2.1) holds for

AEI+(T'+or/2, a), with C=C,

The next result shows that an inequality of the type of (4.2.1) need

only be assumed in a half plane. A similar argument shows that e (q - )

may be replaced by d (q)) in part (b) of Theorem 2.4.1.

e-Cµ-,N)tdt)R(A)udA

4.2. Abstract Parabolic Equations; Analytic Propagators

185

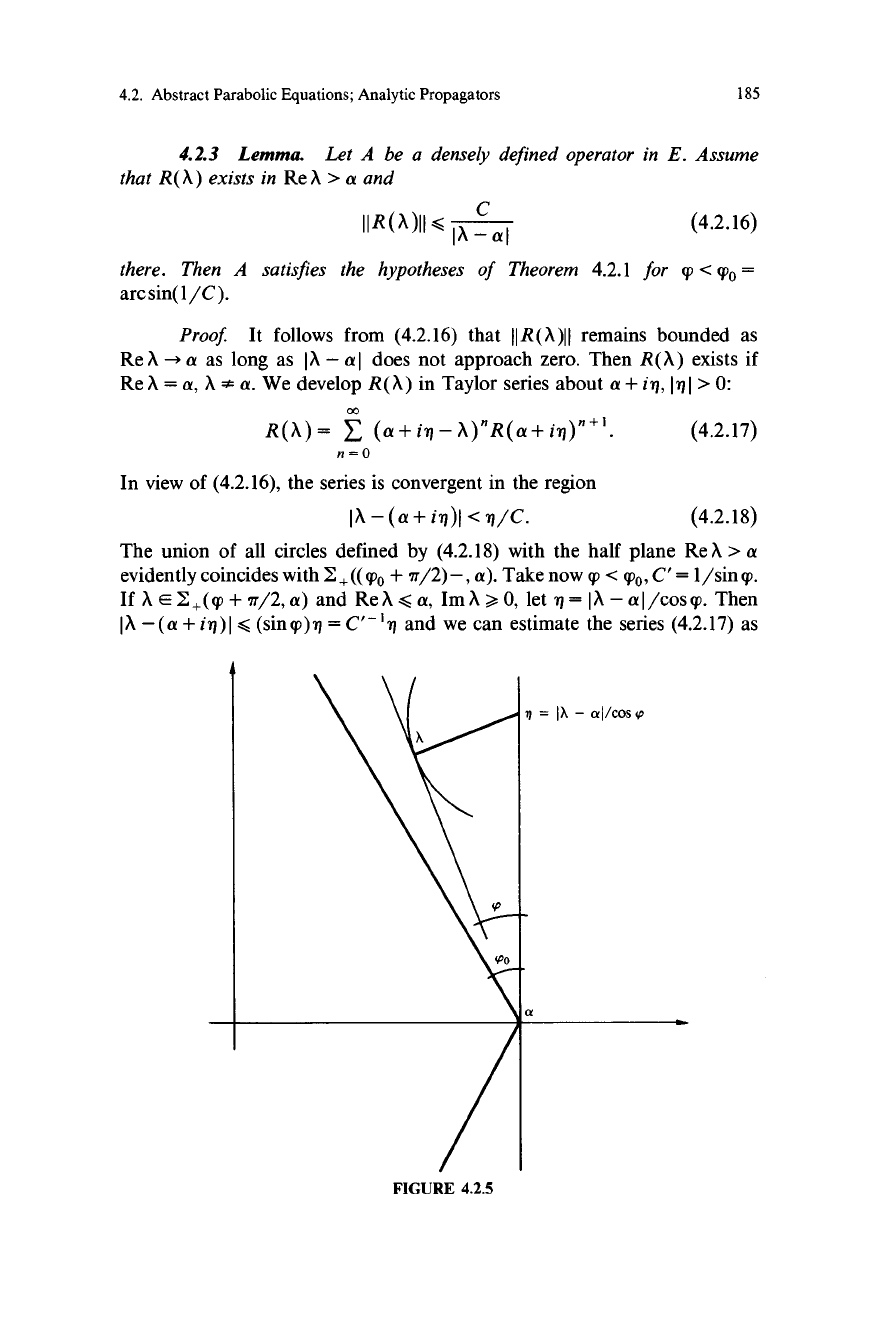
4.2.3 Lemma.

Let A be a densely defined operator in E. Assume

that R(A) exists in Re A > a and

IIR(A)II <

Cal

(4.2.16)

there. Then A satisfies the hypotheses of Theorem 4.2.1 for

q) < qPo =

arc sin(1 IC).

Proof It follows from (4.2.16) that IIR(X)II remains bounded as

Re A - a as long as J X - a I

does not approach zero. Then R (A) exists if

Re A = a, A - a. We develop R(,\) in Taylor series about a+ i q, I

I >O:

R(A)=

(a+irl-A)"R(a+ir1)"+1.

(4.2.17)

n=0

In view of (4.2.16), the series is convergent in the region

lA-(a+ir1)I <r1/C.

(4.2.18)

The union of all circles defined by (4.2.18) with the half plane Re A > a

evidently coincides with I+((q)o + ¶r/2)-, a). Take now qp < quo, C= I /sin q).

If A E E+(p + 7T/2, a) and Re X < a, Im A >,0, let n= IA - a I /cos q). Then

I A - (a + i rl) I < (sin q)) r1= C - i and we can estimate the series (4.2.17) as

FIGURE 4.2.5

186 Abstract Parabolic Equations: Applications to Second Order Parabolic Equations

follows:

C 00

IIR(A)II <

n=0

A-(a+in)

< C °° C _ CC' Cos 4P

4.2.19

C'-C IA-al

( )

A symmetric argument takes care of the case Im A < 0.

The following result, which is a generalization of (half of) Theorem

3.1.8, will be useful in the characterization of operators in the class

lI n C+(0,1).

4.2.4 Theorem. Let A be a densely defined operator in

0: D(A)

E* a duality map. Define

=(AEC;A=(9(u),Au);uED(A),u$0)

(4.2.20)

and let r = r(0; A) be the complement of

Then:

(a) If A E r,

(lull < dist(A, )-'llAu - AulI

(u E D(A)).

(4.2.21)

(b) If A is closed, (Al - A)D(A) is closed for A E r.

(X0I-A)D(A)=E. (4.2.22)

Then r (A0),

the connected component of r that contains Ao

satisfies

r(A0) c p(A)

(4.2.23)

and

IIR(A)ll <dist(A, )-'

(A E r(A0)). (4.2.24)

Proof.

Clearly we only have to prove (4.2.21) for (lull = 1. If A E r,

we have

0 < dist(A, ) < IA - (B(u), Au) I

= I (0(u), Au - Au) I < I10(u)II IIAu - Aull

= IIAu - Aull,

which proves (a). It is plain that (b) is an immediate consequence of (a). To

prove (c), we only have to show that r(A0)n p(A) is both open and closed

in r. That r(A0)n p(A) is open in r is evident. Let (An) be a sequence in

r(A0)n p(A) such that An - A E r. Then there exists 8 > 0 with

dist(An, ; ) >- 8