Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.

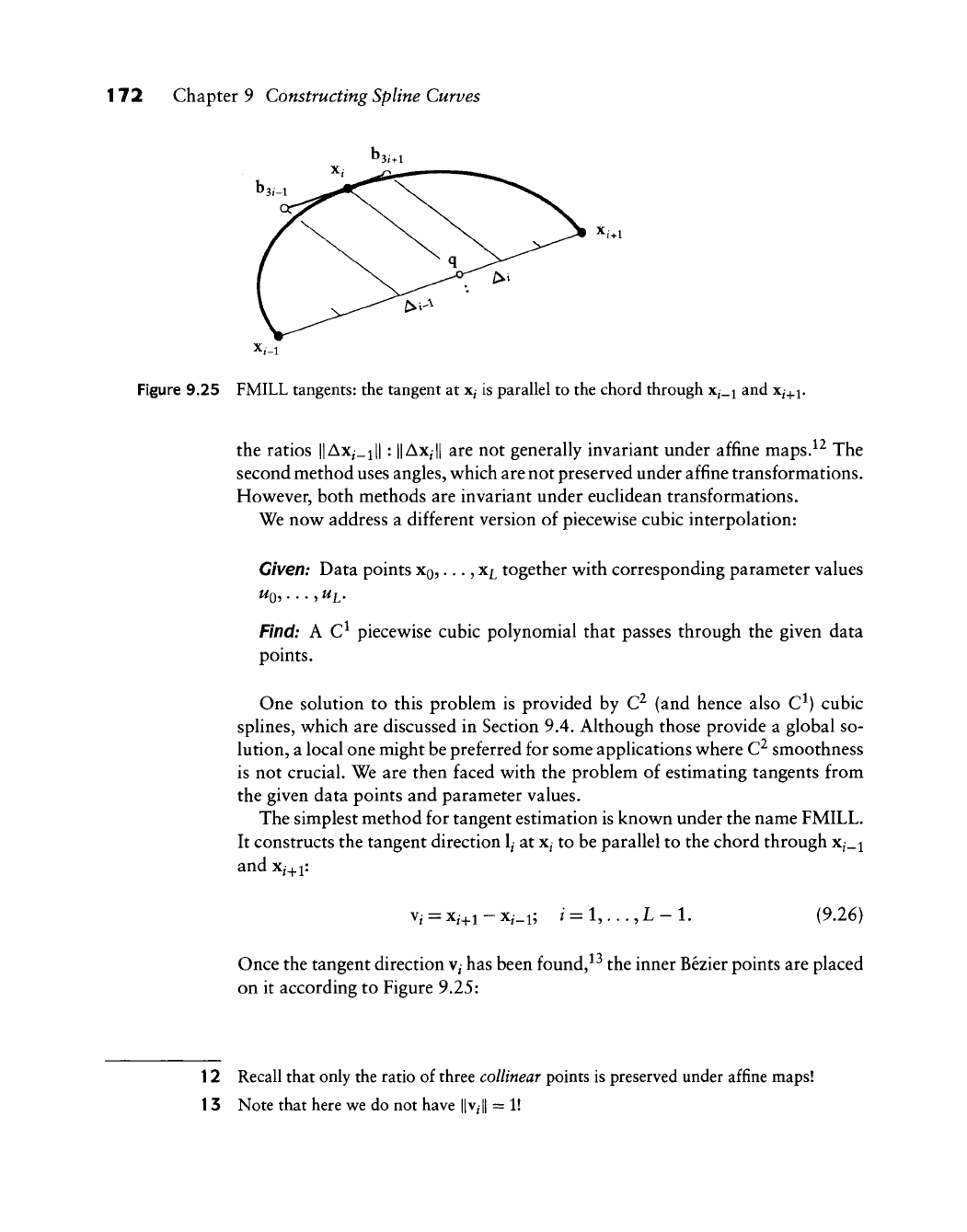
172 Chapter 9 Constructing Spline Curves
Figure 9.25 FMILL tangents: the tangent at
x^
is parallel to the chord through x^_i and Xj^i,
the ratios ||Ax^_i|| : ||Ax^|| are not generally invariant under affine maps.^^ The
second method uses angles, which are not preserved under affine transformations.
However, both methods are invariant under euclidean transformations.
We now address a different version of piecewise cubic interpolation:
Given: Data points
XQ,
...,
xj^
together with corresponding parameter values
WQ,
. . . , Ui.
Find:
A C^ piecewise cubic polynomial that passes through the given data
points.
One solution to this problem is provided by C^ (and hence also C^) cubic
splines, which are discussed in Section 9.4. Although those provide a global so-
lution, a local one might be preferred for some applications where C^ smoothness
is not crucial. We are then faced with the problem of estimating tangents from
the given data points and parameter values.
The simplest method for tangent estimation is known under the name FMILL.
It constructs the tangent direction
1/
at
x^
to be parallel to the chord through x^_i
and Xi^i:
Vi
= Xi^i - Xi_i;
/•
= 1,..., L - 1. (9.26)
Once the tangent direction
V/
has been found,^^ the inner Bezier points are placed
on it according to Figure 9.25:
12 Recall that only the ratio of three
collinear
points is preserved under affine maps!
1
3 Note that here we do not have ||v^|| = 1!

9.8 C^ Piecewise Cubic Interpolation 173
b3.-i-b3,-^^/^-;^
V,, (9.27)
3(A,_i + A,)
b3m = b3,+ .^^ \^yr (9.28)
3(A,_i + A,)
This interpolant is also known as a Catmull-Rom spline.
This construction of the inner Bezier points does not work at
XQ
and x^. The
next method, Bessel tangents, does not have that problem.
The idea behind Bessel tangents^^ is as follows: to find the tangent vector
m^
at
x^, pass the interpolating parabola q/(w) through x^_i,
x^,
x^_^i
with corresponding
parameter values w^_i,
w^,
u^j^i
and let
m^
be the derivative of q^. We differentiate
q, at
Ui',
d , ,
au
Written in terms of the given data, this gives
m,
= ^^^^^x,_, + ^AXi; i=l,...,L-l, (9.29)
A,_i A,-
where
«,=
The endpoints are treated in the same way: mo = d/duqi(uQ)^mi = d/duqi_i(ui),
which gives
mo = 2— mi,
^ Ax^_l
m^ = 2— m^_i.
AL-1
Another interpolant that makes use of the parabolas q^ is known as an
Overhauser spline, after work by A. Overhauser [452] (see also [91] and [154]).
The
i^^
segment s^ of such a spline (defined over
[uj,
W/+i]) is defined by
Si(u) = -^±i q,(M) + —_^q,.+i(M); t = l,...,L-2.
A,- A,-
14 They are also attributed to Ackland [2].

174 Chapter 9 Constructing Spline Curves
In other words, each S/ is a Hnear blend between q/ and q/+i. At the ends, one
sets So(w) = qo(w) and S£^_i(w) = qi-iW.
On closer inspection, it turns out that the last two interpolants are not different
at all: they both yield the same C^ piecewise cubic interpolant (see Problems).
A similar way of determining tangent vectors was developed by McConalogue
[421], [422].
Finally, we mention a method created by H. Akima [3]. It sets
m,- = (1 - Ci)2ii_i + Ci2ii,
where
AX;
A;
and
lAa;
|Aa,_2ll + ||Aa,-||
This interpolant appears fairly involved. It generates very good results, however,
in situations where curves are needed that oscillate only minimally.
9.9 Implementation
The following routines produce the cubic B-spline polygon of an interpolating
C^ cubic spline curve. First, we set up the tridiagonal linear system:
void set_up_system(knot,l,alpha,beta,gamma)
/* given the knot sequence, the linear system for clamped end
condition B-spline interpolation is set up.
Input: knot: knot sequence (all knots are simple; but,
in the terminology of Chapter 10, knot[0]
and knot[l] are of multiplicity three.)
points: points to be interpolated
1:
number of intervals
Output:alpha, beta,gamma: 1-D arrays that constitute
the elements of the interpolation matrix.
Note: no data points needed so far!
V

9.9 Implementation 175
The next routine performs the LU decomposition of the matrix from the
previous routine. (Note that we do not generate a full matrix but rather three
linear arrays!)
void l_u_system(alpha,beta,gamma,],up,low)
/* perform
LU
decomposition
of
tridiagonal system with
lower diagonal alpha, diagonal beta, upper diagonal gamma.
Input: alpha,beta,gamma:
the
coefficient matrix entries
1:
matrix size [0,l]x[0,l]
Output:low: L-matrix entries
up:
U-matrix entries
V
Finally, the routine that solves the system for the B-spline coefficients d^:
solve_system(up,1ow,gamma,1,rhs,d)
/*
solve tridiagonal linear system
of size (1+1)(1+1) whose
LU
decomposition
has
entries
up
and low,
and whose right hand side
is
rhs,
and
whose original matrix
had gamma
as
its
upper diagonal. Solution
is
d[0]
d[l+2].
Input: up,low,gamma:
as
above.
1: size
of
system:
1+1 eqs
in
1+1
unknowns,
rhs:
right hand side, i.e, data points with
end
'tangent Bezier points'
in
rhs[l]
and
rhs[l+l].
Output:d: solution vector.
Note shift
in
indexing from text! Both
rhs and
d
are
from
0 to
1+2.
V
In case Bessel ends are desired instead of clamped ends, this is the code:
void bessel_ends(data,knot,l)
/*
Computes B-spline points data[l]
and
data[l+l]
according
to
bessel
end
condition.
Input: data: sequence
of
data coordinates data[0]
to
data[l+2].
Note that data[l]
and
data[l+l]
are
expected
to
be empty,
as
they will
be
filled
by
this routine.
They correspond
to
the
Bezier points bez[l]
and
bez[31-l].
knot: knot sequence
1: number
of
intervals
Output: data:
now
including ''tangent Bezier points''
data[l],
data[l+l].
*/

176 Chapter 9 Constructing Spline Curves
The centripetal parametrization is achieved by the following routine:
void parameters(data_x,data_y,l,knot)
/*
Finds
a
centripetal parametrization for
a
given set
of 2D data points.
Input: data_x, data_y: input points, numbered from
0 to
1+2.
1: number
of
intervals.
Output: knot: knot sequence. Note:
not
(knot[l]=1.0)!
Note: data_x[l], data_x[l+l] are not used! Same for data_y.
*/
A calling sequence that uses the preceding programs might look like this:
parameters(data_x,data_y,l,knot);
set_up_system(knot,l,alpha,beta,gamma);
1
_u__system
(al
pha,
beta,
gamma,
1,
up,
1
ow);
bessel_ends(data_x,knot,l);
bessel_ends(data_y,knot,l);
sol ve_system(up,low,gamma,!,data_x,bspl_x);
solve_system(up,low,gamma,1,data_y,bspl_y);
Here, we solved the 2D interpolation problem with given data points in data_
X, data_y, a knot sequence knot, and the resulting B-spline polygon in bspl_x,
bspl__y. This calling sequence is realized in the routine c2_spl ine.c.
9.10 Problems
1 For the case of closed curves, C^ quadratic spline interpolation with uni-
form knots does not always have a solution. Why?^^
* 2 Show that interpolating splines reproduce cubic polynomial curves—that
they have cubic precision. This means that if all data points p/ are read off
from a cubic, p^ = c(w^), and the end tangent vectors are read off from the
cubic, then the interpolating spline equals the original cubic.
15 T. DeRose pointed this out to me.

9.10 Problems 177
3 Show that Akima's interpolant always passes a straight line segment
through three subsequent points if they happen to lie on a straight line.
* 4 Show that Overhauser splines are piecewise cubics with Bessel tangents at
the junction points.
* 5 One can generalize the quintic Hermite interpolants from Section 7.6 to
piecewise quintic Hermite interpolants. These curves need first and second
derivatives as input positions. Devise ways to generate second derivative
information from data points and parameter values.
PI Using piecewise cubic C^ interpolation, approximate the semicircle with
radius 1 to within a tolerance of 6 =
0.001.
Use as few cubic segments as
possible. Literature:
[172], [260].
P2 Program the following: instead of prescribing end conditions for interpolat-
ing C^ splines at both ends, prescribe first and second derivatives at
TQ.
The
interpolant can then be built segment by segment. Discuss the numerical
aspects of this method (they will not be wonderful).
This Page Intentionally Left Blank

W. Boehm
Differential
Geometry
I
Uifferential geometry is based largely on the pioneering work of L. Euler
(1707-1783), C. Monge (1746-1818), and C F. Gauss (1777-1855). One of
their concerns was the description of local curve and surface properties such
as curvature. These concepts are also of interest in modern computer-aided
geometric design. The main tool for the development of general results is the use
of local coordinate systems, in terms of which geometric properties are easily
described and studied. This introduction discusses local properties of curves
independent of a possible embedding into a surface.
10.1 Parametric Curves and Arc Length
A curve in E^ is given by the parametric representation
t e[a,b]c]
X
= x(t) =
x(t)
y(t)
z(t)
(10.1)
where its cartesian coordinates x, y, z are differentiable functions of t. (We have
encountered a variety of such curves already, among them Bezier and B-spline
curves.) To avoid potential problems concerning the parametrization of the curve,
we shall assume that
x(t) =
x{t)
m
m
^0,
te
[a,
bl
(10.2)
179

180 Chapter 10 W. Boehm: Differential Geometry I
Xi = X(ti)
a
-o—o—a—o-
Figure 10.1 Parametric curve in space.
where dots denote derivatives vs^ith respect to t. Such a parametrization is called
regular. An example is shown in Figure 10.1
A change x = x{t) of the parameter t^ where r is a differentiable function of
t^ will not change the shape of the curve. This reparametrization will be regular
if f
7«^
0 for all t e [a, fc], that is, we can find the inverse t = ^(r). Let
' =
s(t)=
f ||x
Ja
\\dt (10.3)
be such a parametrization. Because
. . dxdr , dx .
xd^ = -——d^ = -—dr,
dr at dr
s is independent of any regular reparametrization. It is an invariant parameter
and is called arc length parametrization of the curve. One also calls ds = \\x\\dt
the arc element of the curve.
Remark 7 Arc length may be introduced more intuitively as follows: let ti = a-\- iAt and
letA^ > 0 be an equidistant partition of the ^-axis. Let x^ = x{tj) be the corre-
sponding sequence of points on the curve. Chord length is then defined by
(10.4)
where Ax^ = x^.^^
—
x^. It is easy to check that for A^ -^ 0, chord length S
converges to arc length s, while Axj/At converges to the tangent vector x^
at Xj,

10.2 The Frenet Frame 181
Remark 2 Although arc length is an important concept, it is primarily used for theoretical
considerations and for the development of curve algorithms. If, for some appli-
cation, computation of the arc length is unavoidable, it may be approximated by
the chord length (10.4).
10.2 The Frenet Frame
We
w^ill
nov^ introduce a special local coordinate system, linked to a point x(0 on
the curve, that
w^ill
significantly facilitate the description of local curve properties
at that point. Let us assume that all derivatives needed below do exist. The first
terms of the Taylor expansion of x(^ + A^) at t are given by
1 1
x(f + AO =
X
+ xA^ + X-A^^ + X-A^^ + ^
2 6
Let us assume that the first three derivatives are linearly independent. Then
X, X,
X
form a local affine coordinate system w^ith origin x. In this system, x(t) is
represented by its canonical coordinates
A^H-...
lAf^ + ...
v^here . . . denotes terms of degree four and higher in A^.
From this local affine coordinate system, one easily obtains a local cartesian
(orthonormal) system w^ith origin x and axes t, m, b by the Gram-Schmidt process
of orthonormalization, as shov^n in Figure 10.2:
t=^^,
m = bAt, b=^^—^, (10.5)
llxll llxAxll
w^here A denotes the cross product.
The vector t is called tangent vector (see Remark 1), m is called main normal
vector^'^
and b is called binormal vector. The frame (or trihedron) t, m, b is called
the Frenet frame\ it varies its orientation as t traces out the curve.
1 We use the abbreviation
A?-^
= (A?)^.
2 One often sees the notation n for this vector. We use m to avoid confusion with surface
normals, which are discussed later.
